基于Hu向量相似度的图像序列自动排序算法＊

崔克彬，苑津莎，李宝树

（1.华北电力大学控制与计算机工程学院，河北 保定071003；2.华北电力大学电气与电子工程学院，河北 保定071003）

1 引言

全景图像拼接是近年来计算机视觉领域的热点问题，通过将相互间存在重叠区域的图像序列实施配准和融合，并最终形成一幅包含各图像信息的宽视野的、完整的、高分辨率的新图像。为了保证图像序列的正确拼接，必须确定其拍摄顺序，然而，由于拍摄以及后续的存储和处理等过程中图像的排列顺序可能会变得混乱，致使不能直接进行全景图像的拼接。目前，国内外涌现出多种全景图像拼接算法［1～5］，但这些算法在进行拼接前已经知道图像序列的拍摄顺序，如果图像序列的顺序被打乱，则需手工调整排列顺序。

为了避免人工排序费时费力的缺点，利用计算机进行图像序列的自动排序算法被提出。较早关注图像序列自动排序的是文献［6］，算法使用等距离的思想使图像对齐，对齐过程中使用了平移运动模型，但该算法要求相机在拍摄过程中要保持近乎绝对平移，在实际应用中很难做到。文献［7～10］提出了利用相位相关法实现序列图像的自动排序，但文献［7］在确定头尾图像时需人工设定阈值，阈值的大小影响排序效果，不能实现自动化；文献［8］可实现头尾图像的自动识别，但无法完成图像大小不同的序列的自动排序；文献［9］也可实现序列图像的快速、自动排序，但要求图像的大小相同；文献［10］提出了针对不同图像大小的图像序列的自动排序，但并没有考虑在拍摄过程中出现的横拍、竖拍交替拍摄的情况。总体来看，这些算法中，相位相关或其改进算法被广泛应用到自动排序中，但这些方法均未考虑拍摄过程中相机翻转造成的影响。

上述算法存在不能处理拍摄尺寸大小不同或存在图像旋转的图像序列的不足，本文，根据Hu矩对图像旋转具有不变性的特点，定义了Hu矩向量相似度，将其引入图像序列自动排序，解决了这一不足。

2 Hu不变矩

Hu在1962年提出用于描述图像特征的Hu不变矩［11］。矩在统计学中表征随机量的分布，一幅灰度图像可以用二维灰度密度函数来表示，因此可以用矩来描述灰度图像的特征。

一幅M×N的数字图像f（i，j），其p＋q阶几何矩mpq和中心矩μpq的定义见公式（1）和公式（2）：

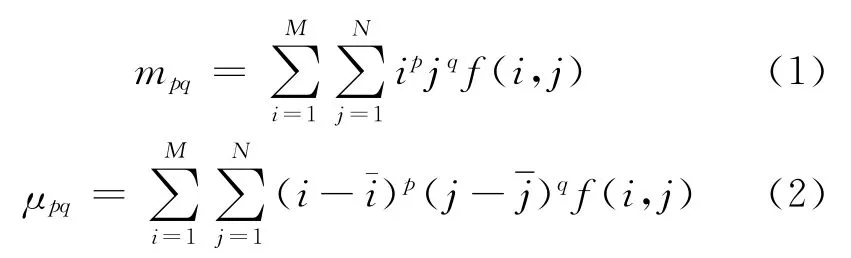
其中，p，q＝0，1，2，…；

为了消除图像比例变化带来的影响，定义规格化中心矩ηpq，见公式（3）：

利用二阶和三阶中心矩可以导出式（4）～式（10）的七个不变矩，它们在图像平移、旋转和比例变化时保持不变。

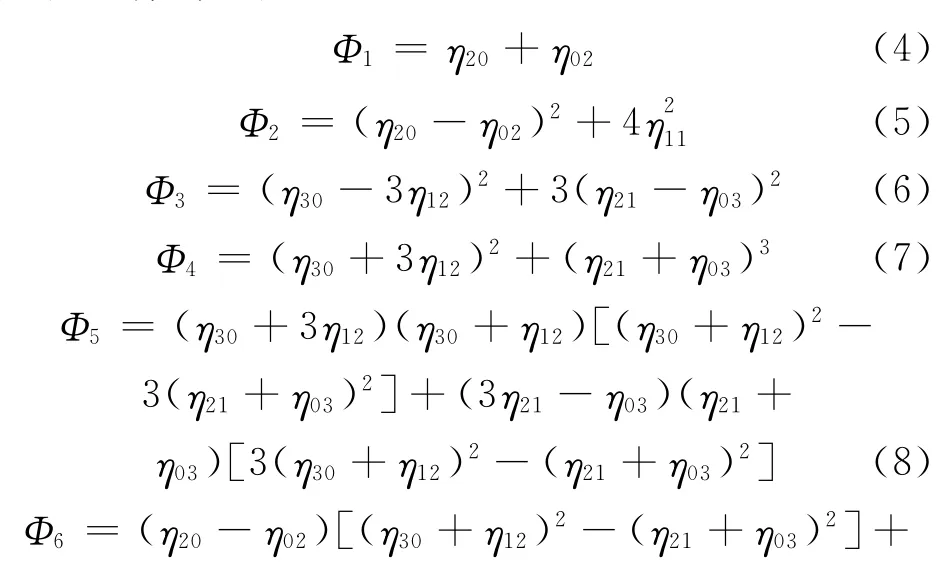
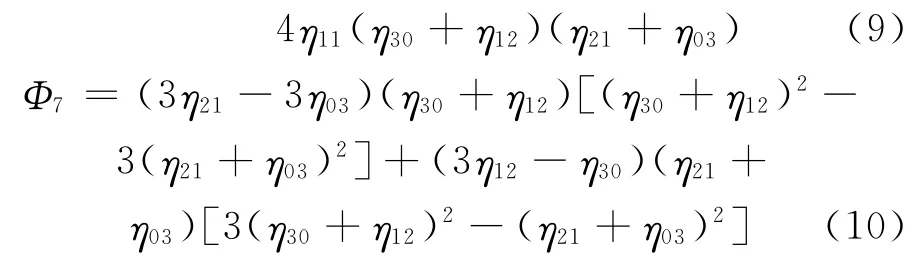
对一幅图像求其七个Hu不变矩，一般得到的结果为绝对值很小的值，因此，在实际使用中对其求对数并取绝对值，即｜logΦi｜，i＝1，2，…，7。图像的Hu 矩信息可以表征图像的本质特征，因此，可利用其实现目标图像的识别［12～15］，但将Hu矩信息应用到序列图像排序中的研究在作者所查阅的文献中未曾见到。

3 基于Hu矩向量相似度的序列图像自动排序

将需要排序的图像转换成灰度图像，根据Hu的七个不变矩每幅灰度图像分别求其七个Hu矩，定义向量HV表示图像的特征。式（11）给出了Hu矩向量HV的定义。

如果两幅图像之间有重叠，则其HV就越相似。对于向量的相似度度量，一般选用欧氏距离法。欧氏距离是一个通常采用的距离定义，是在m维空间中两个点的真实距离。式（12）利用欧氏距离法定义了两幅图像的Hu矩向量的相似度HVS（Hu Vector Similarity）：

其中，i、j表示图像序列的编号，HVS值越小，表示两幅图的Hu矩向量越相似。则两幅图像越相似。当两幅图像完全相同时，其HVS为0，一般地，为了保证两幅图像有一定的重叠，以重叠1/4到1/3为宜。

算法具体步骤为（假定序列图像为n幅）：

（1）确定序列图像的头和尾。

①计算每幅图像和其他n－1 幅图像的HVS。

②对每幅图像选取HVS最小的两个，共2n个值。因为对于头图像和尾图像，其相邻图像为一幅，对于中间图像，其相邻图像为两幅，选取过程中头尾图像按两个相邻图像进行选取。

③找到2n个值中最大的两个，这两个值对应的是图像序列的头和尾。因为在这2n个值中包含两个与头尾图像并没有重叠的图像的HVS，因此它们是最大的两个。

④图像序列中除头尾图像外，其他为中间图像。

（2）序列图像的排序。

①从头、尾图像中任选一幅作为图像序列的开始图像，利用HVS的值找到与其相连的第二幅图像。

②根据第二幅图像的信息，去除与其相连的第一幅（头图像），另一个HVS代表的则是第三幅图像，以此类推，直到所有的图像排序完成。

该方法较相位差方法简单，只是利用现有图像间的HVS即可完成排序，而不必判断图像的左右关系，可直接应用到相位相关算法中，替换原来的求相位差判断两幅图像左右关系的步骤。

4 实验结果与分析

实验1正常拍摄图像实验。

这里所说的正常拍摄是指在拍摄过程中，相机拍摄角度不能调整，即在始终保持横拍或竖拍一种姿势。

图1是正常拍摄的五幅图像，顺序已打乱，图像大小为519×389。

Figure 1 Unordered image set图1 顺序打乱的五幅图像

分别计算图1中五幅图像的Hu矩信息，得到表1中各图像的Hu矩信息。

Table 1 Hu moment information of the images表1 各图像的Hu矩信息

Table 2 HSVvalues of the image set表2 各图像间的HVS

根据表1中Hu矩向量信息，利用式（12）计算各图像间的HVS，得到表2。HVS具有对称性，即图像i和图像j的HVS与图像j和图像i的HVS相同，因此表2中对图像i和图像j的HVS只列出了一个，且图像i与自身的HVS未列出，未列出用“/”表示。

根据表2，找到每幅图像对应的最小的两个HVS及其对应的图像编号，构造表3。

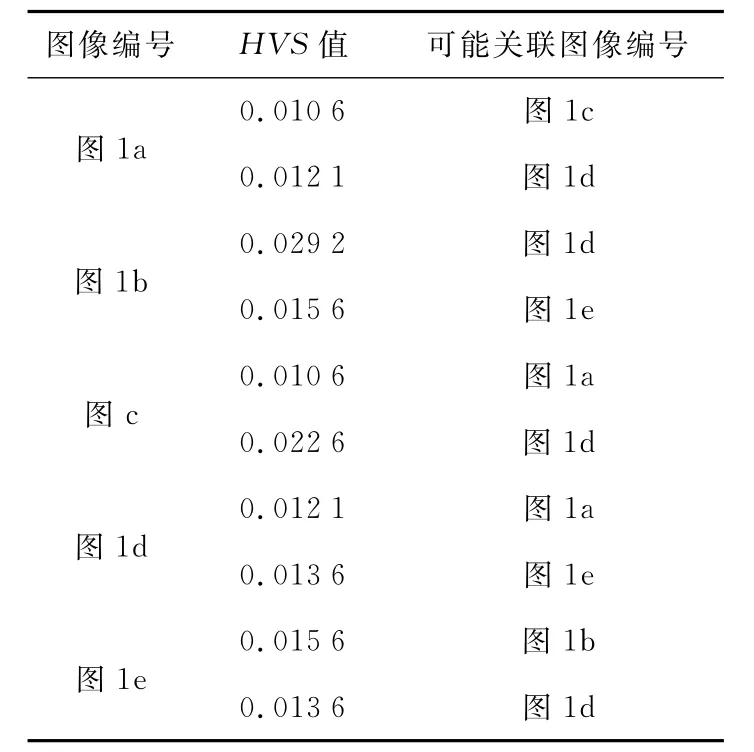
Table 3 Possible image SNand HSVvalues of the images表3 各图像可能相邻的图像编号及HVS值

根据表3中HVS值的情况，确定图1b和图1c中存在两个最大值，因此可以判断这两幅图像为图像序列的头图像和尾图像。选定图1b为头图像，则根据表3中第二列的信息，可推断出与图1b相连的是图1e，接着找到与图1e的相邻图像编号（包括图1b 和图1d），图1b 已经在图1e的一侧了，因此，图1e的另一侧应该为图1d，依此类推，直到所有的图像排序完毕。最终的排序结果为图1b→图1e→图1d→图1a→图1c，图2给出了排序好的图像序列。

Figure 2 Sorted image set图2 排序后的图像序列

为了验证本文算法的有效性，与文献［8］中的相位差法做了对比，表4给出了图像序列的相位相关信息。

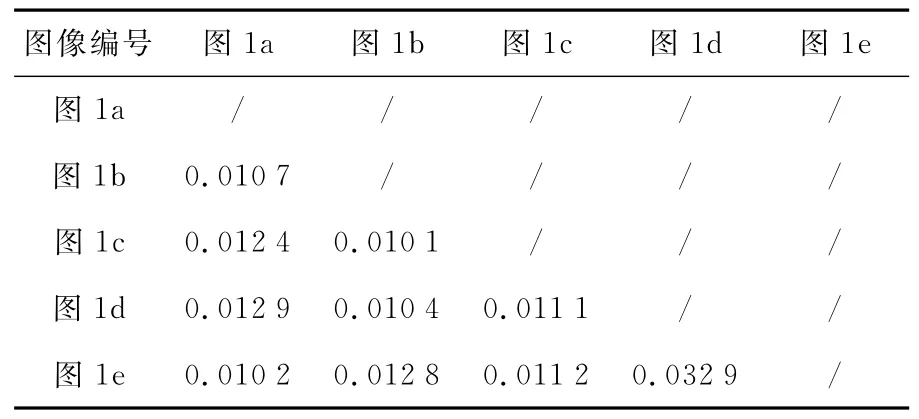
Table 4 Phase correlation information of the image set表4 各图像相位相关信息

利用文献［8］算法分析表4发现，利用相位相关方法得到了与本文相同的头、尾图像和中间图像，对于图像序列的排序，利用本文给出的方法或是相位差法均可得到和本文一致的排序结果。假定图像的大小为M×N，利用相位差方法时由于用到了卷积，其时间复杂度为O（（M×N）2）级，而本文求Hu矩采用的是点乘的方式，其时间复杂度为O（M×N）级，算法时间复杂度上本文给出的算法较优。

实验2将图像序列的某一幅图像右旋转90°的实验

在进行图像拍摄时经常出现横拍和竖拍交替进行的情况，如果图像序列中出现了同时包含这两种拍摄方式时，则拍摄图像的尺寸大小不同。对于这种情况，文献［10］给出了一种改进的相位差法用于计算相位相关，该方法通过将两幅图像补零的方式达到尺寸大小一致，但这无疑增加了算法本身的时间复杂度，同时，该文献中大小不同的两幅图像也不能存在旋转情况。本文给出的算法依靠图像的Hu矩向量来判断两幅图像的相似性，与图像本身的大小无关，且Hu矩向量对图像的大小具有旋转不变性。因此，在右旋转90°时，其Hu矩向量不变，因此，其计算结果与实验1完全相同，时间复杂度没有变化，排序结果也与实验1完全相同。

实验3将图像序列的某一幅图像旋转180°的实验。

在进行图像拍摄时竖拍有头部向左和向右倾斜两种方式，可认为是旋转180°的情况，因此有必要做旋转180°的实验，对图像序列的第一幅图像旋转180°，重新计算其与其他图像的相位相关信息，计算结果见表5。

根据文献［8］中的算法分析表5发现，得到的

结果与实验1已不完全相同。而对于本文给出的算法，由于Hu矩向量的旋转不变性，第一幅图像的Hu矩信息未发生改变，因此实验结果与实验1完全相同。

Table 5 Phase correlation information of the image set after a right rotation of 180degrees of image a表5 图1a的图像右旋转180°后各图像的相位相关信息

从上面三组实验可以看出，基于Hu不变矩的序列图像自动排序算法具有良好的全自动排序功能，时间复杂度低，且序列图像尺寸大小不同时可在不增加时间复杂度的情况下正常处理，对于图旋转180°时仍能正确给出排列顺序。

根据表3 中HVS值的情况，确定图1b 和图1c中存在两个最大值，因此可以判断这两幅图像为图像序列的头图像和尾图像。选定图1b为头图像，则根据表3中第二列的信息，可推断出与图1b相连的是图1e，接着找到与图1e的相邻图像编号（包括图1b 和图1d），图1b 已经在图1e的一侧了，因此，图1e的另一侧应该为图1d，依此类推，直到所有的图像排序完毕。最终的排序结果为图1b→图1e→图1d→图1a→图1c，图2给出了排序好的图像序列。

5 结束语

本文提出了一种新的对顺序杂乱的图像序列进行自动排序的算法，利用Hu 矩构造了图像的HVS，根据图像间HVS的大小判断两幅图像是否相邻，并根据图像间的相邻关系确定图像序列的顺序。实验结果表明，算法的鲁棒性较强，不仅能针对拍摄尺寸大小相同的图像序列处理，而且对拍摄过程中出现的拍摄角度旋转90°和180°的情况也能正常处理，具有较强的实用性，且算法时间复杂度低于常见的相位差法。但是，算法在首尾图像有重叠的情况下并不适用，这也是本文进一步要解决的问题之一。

［1］ Yang Fan，Deng Zhen－sheng，Fan Qiu－hong.A method for fast automated microscope image stitching［J］.Micron，2013，48：17－25.

［2］ Xiong Yin－gen，Pulli K.Fast panorama stitching for highquality panoramic images on mobile phones［J］.IEEE Transactions on Consumer Electronics，2010，56（2）：298－306.

［3］ Zhong Min，Zeng Ji－guo，Xie Xu－sheng.Panorama stitching based on SIFT algorithm and levenberg－marquardt optimization［J］.Physics Procedia，2012，33：811－818.

［4］ Huang Ying－dong，Li Jie，Fan Ning－jun.Aerial image mosaic algorithm of MAV［J］.Opto－Electronic Engineering，2008，35（9）：99－104.（in Chinese）

［5］ He Jing，Li Yong－shu，Lu Heng，et al.Research of UAV aerial image mosaic based on SIFT［J］.Opto－Electronic Engineering，2011，38（2）：122－126.（in Chinese）

［6］ Jang K H，Jung S K，Lee M.Constructing cylindrical panoramic image using equidistant matching［J］.Electronics Letters，1999，35（20）：1715－1716.

［7］ Zhao Hui，Chen Hui，Yu Hong.An improved fully－automatic image mosaic algorithm［J］.Journal of Image and Graphics，2007，12（2）：336－342.（in Chinese）

［8］ Zhao Wan－jin，Gong Sheng－rong，Liu Quan，et al.An autosorting arithmetic for image sequence used in image mosaics［J］.Journal of Image and Graphics，2007，12（10）：1861－1864.（in Chinese）

［9］ Song R，Szymanski J.Auto－sorting scheme for image ordering applications in image mosaicing［J］.Electronics Letters，2008，44（13）：798－799.

［10］ Wu Xian－xiang，Guo Bao－long，Wang Juan.An improved automatic image sequencing algorithm［J］.Journal of Optoelectronics·Laser，2009，20（8）：1114－1117.（in Chinese）

［11］ Ming－Kuei H.Visual pattern recognition by moment invariants［J］.IRE Transactions on Information Theory，1962，8（2）：179－187.

［12］ Zhang Ming－heng，Han Yue－lin，Zhao Yi－bing，et al.Road traffic signs recognition based on improved Hu moment invariants［J］.Journal of Dalian University of Technology，2012，52（6）：908－913.（in Chinese）

［13］ Zhang Yuan，Cheng Wan－sheng，Zhao Jie.Classification of surface defects of strips based on invariable moment functions［J］.Opto－Electronic Engineering，2008，35（7）：90－94.（in Chinese）

［14］ Zhao Feng－min，Liu Hao，Chen Wang－da.Method for ship target recognition in mid－long range［J］.Laser ＆Infrared，2012，42（9）：1071－1075.（in Chinese）

［15］ Liu Zheng－jun，Li Qi，Wang Qi.Object recognition of ladar range image using combined moment invariants［J］.Chinese Journal of Lasers，2012，39（60）：193－199.（in Chinese）

附中文参考文献：

［4］ 黄英东，李杰，范宁军.微小型飞行器航空图像拼接算法［J］.光电工程，2008，35（9）：99－104.

［5］ 何敬，李永树，鲁恒，等.基于SIFT 特征点的无人机影像拼接方法研究［J］.光电工程，2011，38（2）：122－126.

［7］ 赵辉，陈辉，于泓.一种改进的全景图自动拼接算法［J］.中国图象图形学报，2007，12（2）：336－342.

［8］ 赵万金，龚声蓉，刘全，等.一种用于图像拼接的图像序列自动排序算 法［J］.中 国 图 象 图 形 学 报，2007，12（10）：1861－1864.

［10］ 吴宪祥，郭宝龙，王娟.一种改进的序列图像自动排序算法［J］.光电子·激光，2009，20（8）：1114－1117.

［12］ 张明恒，韩月林，赵一兵，等.基于改进Hu不变矩的路面交通标识识别［J］.大连理工大学学报，2012，52（6）：908－913.

［13］ 张媛，程万胜，赵杰.不变矩法分类识别带钢表面的缺陷［J］.光电工程，2008，35（7）：90－94.

［14］ 赵峰民，刘皞，陈望达.中远距离舰船目标识别方法研究［J］.激光与红外，2012，42（9）：1071－1075.

［15］ 刘正君，李琦，王骐.基于组合矩的激光雷达距离像目标识别［J］.中国激光，2012，39（60）：193－199.