长波长垂直腔面发射激光器开关及双稳特性

李林福，陈建军

(1.贵州民族大学信息工程学院，贵阳550025;2.新疆医科大学医学工程技术学院，乌鲁木齐830011)

引 言

近年来，垂直腔表面发射激光器(vertical cavity surface emitting laser，VCSEL)被广泛用于全光信号处理系统，光网络互连系统。相比于传统的边发射激光器，VCSEL具有低成本、能量低损耗、单纵模圆形光束输出、易与光纤耦合、易集成阵列等优良性能，正逐渐成为光通信和光信号处理的理想器件［1-4］。由于VCSEL激光腔的结构对称性和增益介质很弱的各向异性，这会使出射光沿相互正交光轴的其中一个方向激射，导致横磁模极化偏振的产生。并且极化偏振光具有模式不稳定性，注入电流与温度的变化可以使偏振光模式出现转换。在可调外部激光器线性偏振光注入下，可使注入光偏振方向与VCSEL自由运行时被抑制的极化模偏振方向相同(称为正交光注入)，而与激射模偏振方向相反，此时光场之间的相互作用会强烈影响腔内横模和极化模的特性，出现偏振开关的现象［5-7］;如果改变正交注入光的频率变化方向，比如逐渐连续增大注入光频率或连续减小注入光频率，就可通过注入光频率的变化诱导产生偏振双稳现象。考虑到合理控制偏振开关和偏振双稳现象在光开关、光存储和全光信号处理中的潜在重要应用，VCSEL的偏振转换和双稳特性一直是研究者关注的焦点［8-15］。

近年来，许多学者对外部光注入条件下850nm VCSEL中偏振开关和偏振双稳特性进行了研究［12-15］，这些研究表明:由于短波长VCSEL内极化模式间隔小，其偏振模式对电流或温度等条件改变非常敏感，外部光注入时的偏振转换及双稳特性都较为复杂。相比于前者，长波长VCSEL有较宽的极化模式间隔，且外部光注入时产生偏振开关效应更为稳定且偏振转换速度非常快，由此产生的偏振双稳效应相对而言易于实现，更适合用于全光信号处理系统［7-8］。因此，研究长波长VCSEL在外部自由度引入时偏振开关和偏振双稳的特性具有非常广泛的应用价值和现实意义。基于此，结合前面的相关工作［15-16］，本文中基于拓展的自旋反转模型，对正交光注入1550nm VCSEL的偏振开关和偏振双稳特性进行了数值仿真和相关理论分析。

1 理论模型

图1为外部正交光注入1550nm VCSEL的系统模型示意图。可调谐半导体激光器发出的光经过可调光衰减器(variable optical attenuator，VOA)、偏振控制器(polarization controller，PC)和光纤耦合器(coupler)后分成两部分:一部分进入光功率计(optical power meter，OPM)内以便于探测注入光功率大小;另一部分经光环行器(optical circulator，OC)注入到1550nm VCSEL 内，光谱仪(optical spectrum analyzer，OSA)探测分析最后的输出信号。

Fig.1 Schematic diagram of orthogonal optical injection in a VCSEL system

根据自旋反转模型，同时考虑正交光注入以及噪声对激光器的影响，描述VCSEL非线性动力学特性的速率方程可以写为［10］:

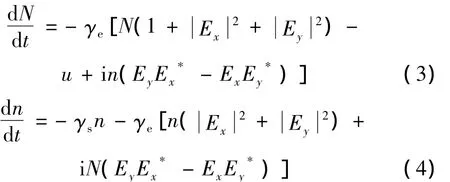
式中，E表示激光器的慢变场复振幅，E*表示E的复共轭，下标x，y分别表示x和y方向的线偏振模式，N是导带和价带之间总的反转粒子数，n表示两个自旋反向的反转粒子数之差，k代表光场衰减率，α是线宽增强因子，γe为反转粒子数N总的衰减率，γs为自旋反转速率，γa代表有源介质线性二向色参量，γp代表有源介质线性双折射参量，u表示归一化的注入电流，相应的u=1对应阈值电流，Einj(t)是正交注入光的场振幅，kinj代表正交极化方向上的注入耦合系数，Δω=ωinj-(ωx+ωy)/2(ω表示线性偏振模的角频率，ωinj表示正交极化方向注入光的角频率)是极化注入光与VCSEL两个偏振模中心频率的角失谐频率。方程组中，(1)式和(2)式的最后一项为自发辐射噪声项，其中，βsp是自发辐射速率，ξ+(t)和ξ-(t)为独立的高斯白噪声，其平均值为0，方差为1。为了后面表述简便，采用Δνx=νinj-νx表示外部可调谐激光器的正交极化注入光与VCSEL光场内x线性偏振模的频率失谐，用P=表示注入或输出光功率，具体取决于不同的角标。

2 数值仿真分析

通过4阶龙格-库塔方法对常微分方程组(1)式～(4)式进行数值求解，数值模拟参量取值为［9］:α=3．0，k=300ns-1，γe=1ns-1，γa=1ns-1，γp=192.1ns-1，γs=1000ns-1，kinj=300ns-1，ω =1.2161 ×1015rad/s(中心频率所对应的波长为 1550nm)，βsp=10-6，u，Δνx，Pinj(光注入强度)为自由选择参量。

2．1 正交光注入1550nm VCSEL频率诱导偏振开关与双稳特性

Fig.2 a—P-u curve of a VCSEL at free running b—bifurcation diagram of P versus frequency detuning Δνx

图2a中给出了自由运行状态下VCSEL的x和y方向线性偏振模式输出功率Px和Py与归一化注入电流u的变化曲线。其中黑色点表示y模输出状态，浅灰色点表示x模输出状态，图2b和图2a是一致的。从图中可以看出，在整个注入电流变化区域，主激射模始终为y模，x模始终被抑制。因此这里考虑外部注入光的偏振模式为x模(正交光注入)，图2b中给出了正交光注入强度一定的情况下，x和y线性偏振(linear polarization，LP)模随频率失谐量变化时的分岔图。从图2b中容易看出，当处于较大的负频率失谐时(Δνx:-30GHz→ -12GHz)，Py近似等于 1，而相应的Px值趋于0。这说明此时y模仍然为主激射模，此时x模几乎被完全抑制。这是由于注入光与VCSEL内x模的失谐较大，外部光场与VCSEL腔内光场非线性相互作用较弱，不足以使被抑制的x模激射。随着负频失谐量减小(Δνx:-11GHz→ -8GHz)，Px和 Py的值出现跳变，x模开始激射，两模式竞争非常激烈，呈现出复杂的混沌共存特征。但当失谐量Δνx进一步在负频方向减小时，主激射模由y模突然跳变为x模，出现明显的偏振开关现象。考虑到此时开关出现在整个失谐区域的左侧，因此称此类开关为左侧偏振开关。随着失谐量继续向正频失谐方向增加(Δνx:-8GHz→8GHz)，Px变化明显，这一过程中，主激射模x经历了注入锁定、倍周期分岔和混沌等一系列极化动态演化过程。对于较大的正失谐量(Δνx＞8GHz)，Py较大，此时的Px值趋于0。说明较弱的非线性相互作用会导致主激射模由x模向y模跳变，与上述定义类似，把此类开关称为右侧偏振开关。

图3所示为正交光注入强度一定时，通过连续改变频率失谐量Δνx所得的VCSEL两个模式的偏振双稳图形。从图中可以看出，在Δνx向正频失谐方向增加过程中(Δνx:-30GHz→30GHz)，由于外部注入光场与VCSEL腔内模式之间的非线性相互作用，会导致x模和y模出现左侧和右侧两类偏振开关。通过改变Δνx的 扫 描 方 向，即 降 低 Δνx(Δνx:30GHz→-30GHz)，这两类偏振开关现象也可产生，但偏振开关点的位置由于VCSEL输出具有记忆效应，导致此时腔内非线性作用与前者并不重合，从而在零频率失谐量(Δνx=0)的左侧和右侧产生类似磁滞回线的现象，即偏振双稳效应。进一步的观察细节还可以发现，左侧与右侧偏振双稳宽度并不相等，且对于两个线偏振模式而言，左侧偏振双稳效应几乎完全相同，表现为Px增大时同在左侧的Py相应减小，右侧也有同样的现象，这主要归因与两个模式相对应的涨消能量分布。

Fig.3 Polarization bistability of different frequency detuning

2．2 光注入强度及偏置电流变化对频率诱导偏振双稳的影响

VCSEL在外部正交光注入下，外部条件的改变会使其输出特性发生明显变化，同时其偏振双稳特性也将受到影响，因此这里考虑改变光注入强度及偏置电流的大小来研究频率诱导偏振双稳的相关特性。图4所示为偏置电流不变(u=1.5，归一化量无单位)时，注入光强度 Pinj(归一化量无单位)分别为0.015，0.05，0.12时x模和y模的偏振双稳图样。由图4中的第1行可以看出，光注入强度较小时(Pinj=0.015)，仅左侧偏振双稳现象出现，并且曲线中间区域存在跳变振荡现象，说明在两类偏振开关之间存在模式共存现象。当光注入强度较大时(Pinj=0.05，0.12)，右侧偏振双稳现象显现，而且随着注入光强度增加，实线和点划线中间间隔变大，表明偏振双稳宽度有逐渐增大的趋势。相比而言，左侧偏振双稳宽度则呈现出先减小后增大的变化趋势。由图4中的第1列或第2列还可发现，对于较大的注入强度，曲线中间区域也较宽，表明两类偏振开关之间的区域宽度相应也较大，这主要是由于高注入强度允许x模在较大的频率失谐范围内形成主激射状态。

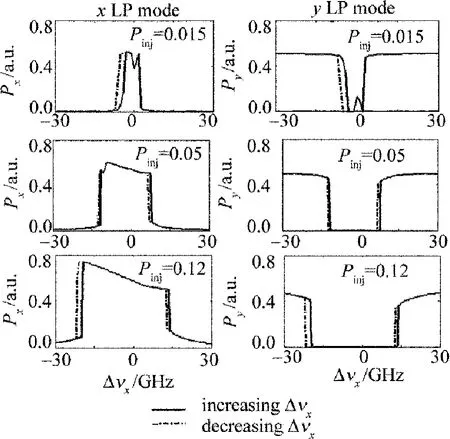
Fig.4 Polarization bistability of different optical injection

图5 为光注入强度不变时(Pinj=0.10)，偏置电流u分别为1．5，3．0和4．0时 x模和 y模的偏振双稳曲线。如图所示，偏置电流的变化对偏振双稳的影响非常显著。对于右侧，随注入电流增大，实线和点划线间隔变大，表明较大的偏置电流可以导致右侧偏振双稳宽度呈现明显增加的趋势。随注入电流增大，左侧双稳一直存在间隔，但宽度变化趋势不明显，表明注入电流对左侧偏振双稳现象影响有限，且不如对右侧双稳影响明显。随注入电流增加，Px和Py的峰值在增大，表明大电流条件下会使处于主激射的模式具有较大的输出强度;零失谐量左右两边曲线跳变间隔区域增加，表明较大电流加大了两类偏振开关之间的区域宽度。

Fig.5 Polarization bistability at different bias current

Fig.6 Polarization bistability width vs.different intensity of light injection

为了能够更全面地了解光注入强度与偏置电流的变化对频率诱导偏振双稳(polarization bistability，PB)的影响，图6中给出了不同偏置电流作用时，VCSEL左侧与右侧偏振双稳宽度随光注入强度的变化关系曲线。如图6a所示，对于不同的偏置电流情况，左侧偏振双稳宽度随注入光强增加呈现明显的波动，且在整个注入强度区域存在极大值。当偏置电流增加时，此偏振双稳宽度极大值也随之增加。由图6b中可以看出，随着注入光强度的增强，不同的偏置电流情况下右侧偏振双稳宽度总体呈现逐渐增加的趋势，且在较大的注入强度下表现出一定的饱和效应。当光注入强度一定时，偏置电流的增加可以显著提高偏振双稳宽度，这一现象在较大的光注入强度下(Pinj＞0.06)表现尤为明显。

3 结论

基于自旋反转模型，对正交光注入下1550nm VCSEL频率诱导偏振开关和偏振双稳特性进行了数值研究。研究结果表明:在正交光注入情况下，连续地增加或减小注入光与VCSEL光场内x线性极化模的频率失谐量可诱发产生两类偏振开关和偏振双稳效应。当注入光强度增加时，两类偏振开关之间的区域将增大，且VCSEL的主激射模的输出功率也呈现增加的趋势，同时左侧与右侧的偏振双稳宽度也会随之变化。另外，偏置电流的变化也会显著改变左侧与右侧的偏振双稳宽度和VCSEL光场的输出功率。相比于左侧偏振双稳宽度的变化，不同偏置电流作用时右侧偏振双稳宽度随注入光强的变化呈现出更好的规律性。因此在实际应用过程中，可根据需要合理的控制光注入强度与偏置电流，以实现对1550nm VCSEL频率诱导偏振开关与偏振双稳特性的控制。

［1］ SAKAGUCHI J， KATAYAMA T， KAWAGUCHI H.All-optical memory operation of 980nm polarization bistable VCSEL for 20Gb/s PRBS RZ and 40Gb/s NRZ data signals［J］.Optics Express，2010，18(12):12362-12370.

［2］ SALVIDE M F，MASOLLER C，TORRE M S.All-optical stochastic logic gate based on a VCSEL with tunable optical injection［J］.IEEE Journal of Quantum Electronics，2013，49(10):886-893.

［3］ PéREZ P，VALLE A，PESQUERA L，et al.All-optical inverter based on polarization switching in VCSELs subject to single and dual optical injection［J］.IEEE Journal of Selected Topics in Quantum E-lectronics，2013，19(4):1700408.

［4］ CHEN X H，LIN X D，WU Z M，et al.Optical generation of highquality millimeter-wave based on an optically injected VCSEL subject to polarization-rotated external optical feedback［J］.Acta Physica Sinica，2012，61(9):094209(in Chinese).

［5］ YANG B X，XIA G Q，LIN X D，et al.Polarization switching performance of VCSEL subjected to optical pulse injection［J］.Acta Physica Sinica，2009，58(3):1480-1483(in Chinese).

［6］ VALLE A，GATARE I，PANAJOTOV K，et al.Transverse mode switching and locking in vertical-cavity surface-emitting lasers subject to orthogonal optical injection［J］.IEEE Journal of Quantum Electronics，2007，43(4):322-333.

［7］ TORRE M，HURTADO A，QUIRCE A，et al.Polarization switching in long-wavelength VCSELs subject to orthogonal optical injection［J］.IEEE Journal of Quantum Electronics，2011，47(1):92-99.

［8］ AL-SEYAB R，SCHIRES K，KHAN N A，et al.Dynamics of polarized optical injection in 1550nm VCSELs:theory and experiments［J］.IEEE Journal of Selected Topics in Quantum Electronics，2011，17(5):1242-1249.

［9］ PANAJOTOV K，GATARE I，VALLE A，et al.Polarization-and transverse-mode dynamics in optically injected and gain-switched vertical-cavity surface-emitting lasers［J］.IEEE Journal of Quantum E-lectronics，2009，45(11):1473-1481.

［10］ SAN MIGUEL M，FENG Q，MOLONEY J V.Light-polarization dynamics in surface-emitting semiconductor lasers［J］.Physical Review，1995，A52(2):1728-1739.

［11］ RYVKIN B S，PANAJOTOV K，AVRUTIN E A，et al.Optical-injection-induced polarization switching in polarization-bistable vertical-cavity surface-emitting lasers［J］.Journal of Applied Physics，2004，96(11):6002-6007.

［12］ SCIAMANNA M，PANAJOTOV K.Route to polarization switching induced by optical injection in vertical-cavity surface-emitting lasers［J］.Physical Review，2006，A73(2):023811.

［13］ ZHANG W L，PAN W，LUO B，et al.Polarization switching and hysteresis of VCSELs with time-varying optical injection［J］.IEEE Journal of Selected Topics in Quantum Electronics，2008，14(3):889-894.

［14］ GATARE I，SCIAMANNA M，NIZETTE M，et al.Mapping of twopolarization-mode dynamics in vertical-cavity surface-emitting lasers with optical injection［J］.Physical Review，2009，E80(2):026218.

［15］ LI L F，CHEN J J，CHEN N.Nonlinear analysis of VCSEL subject to optical injection and feedback［J］.Laser Journal，2013，34(3):9-11(in Chinese).

［16］ LI L F.Chaos and chaotic synchronization in light injected multimode semiconductor lasers［J］.Laser Technology，2013，37(3):330-333(in Chinese).