弯曲长周期光子晶体光纤光栅传感器的研究

余先伦，张仔兵，屈 勇，舒纯军

(1.重庆三峡学院信息与信号处理重点实验室，万州404000;2.重庆信息技术职业学院，万州404000)

引 言

光纤光栅传感器具有高分辨率、高精确性、电磁干扰影响低的特征，以及在传感点不产生电火花和不需要电功率支持等优点。光子晶体光纤(photonic crystal fiber，PCF)是由纤芯和周期排列的微平行孔包层构成的介质，强烈地依赖于设计细节，具有独特的传光特性，能够改进光纤通信系统和新型光电设备的性能［1-5］。PCF光栅主要利用沿PCF长度方向周期折射率或几何结构的扰动特性，能够兼具光纤光栅和PCF的特性，在航天工程、自动控制、油井监测及道路桥梁健康检测等诸多领域有广泛潜在价值。当前国际国内制作的PCF光栅主要有两类，PCF布喇格光栅和长周期PCF光栅。PCF布喇格光栅的光栅周期大约为1μm，能够用于温度和压力传感器中。长周期PCF光栅的光栅周期大约在100μm，具有很低的温度敏感性，可以不进行温度补偿［6-7］。

弯曲传感器是PCF光栅发展的一个重要方向。弯曲长周期光子晶体光纤光栅传感器主要利用光栅受到外界压力作用时会产生弯曲，在光栅中传播的光脉冲能量产生损耗和谐振波长发生漂移，通过检测能量损耗和波长漂移量就能够方便检测出外界参量的改变［8-9］。弯曲长周期光子晶体光纤光栅传感器机械光学转换部件少，光路封闭，在水下运动物体监测、各种危险火灾预警系统及建筑道路结构健康检测中有着广泛应用。

作者根据弯曲长周期光子晶体光纤光栅传感器的工作原理，设计出一般弯曲长周期光子晶体光纤光栅传感器系统，计算了长周期光子晶体光纤光栅弯曲传感器有效折射率与弯曲的关系，计算了弯曲量与长周期光子晶体光纤光栅横向和径向应变的关系，计算了长周期光子晶体光纤光栅弯曲传感器谐振波长漂移量与弯曲的关系。

1 长周期光子晶体光纤光栅理论模型

假设PCF纤芯由纯硅构成，包层由周期性排列的空气圆孔组成，长周期光子晶体光纤光栅折射率的扰动仅沿光纤长度方向，在长周期光子晶体(long period photonic，LPG)光纤光栅中，模式耦合主要发生在基波导模和同向传导包层模之间，其耦合模方程是［1］:

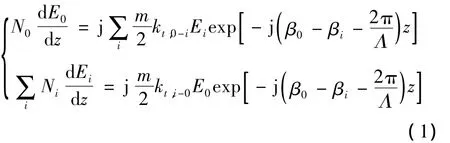
式中，E0，Ei表示基模和第 i阶包层模的振幅;β0，βi表示它们的传播常数;m表示包层模角阶数;Λ表示长周期光子晶体光纤光栅周期;z表示光脉冲传播距离;kt，0-i是长周期光子晶体光纤光栅基模和第i阶包层模之间横向耦合系数(t泛指一种耦合度)，可表示为:

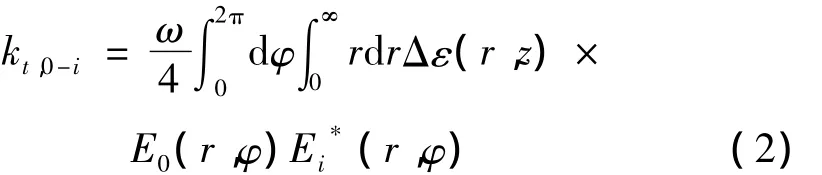
式中，ω为脉冲角频率，Δε(z)指光栅折射率的微小改变引起的介电系数的变化量，E0(r，φ)和 Ei*(r，φ)表示基模振幅和第i阶包层模的复振幅，*表示复共轭。

根据耦合模理论，长周期光纤光栅中模式耦合主要发生在正向传播的模式之间，它们之间的失谐参量可定义为:

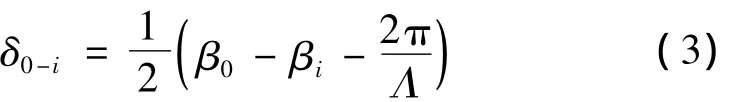
失谐参量表征基模和包层模间相位匹配的偏离，越靠近共振发生的条件，耦合越强。只考虑失谐参量很小的模式，结合边界条件和数值方法即可求解耦合模方程(1)式，求得相关光谱范围内各个波长处的透射率，得到长周期光子晶体光纤光栅的透射谱。这种方案在一般情形下足够精确并能获得直观的解析解和传输系数。

根据耦合模理论对(1)式求解，在Descartes坐标系中，长周期光子晶体光纤光栅沿长度方向模场分布可表示为:

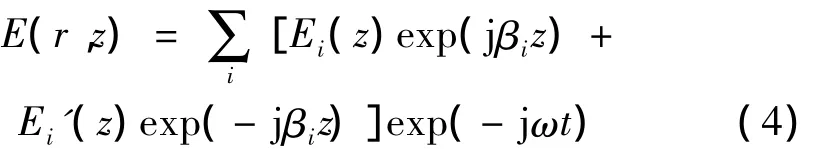
式中，Ei和Ei′表示第i阶模沿+z和-z方向传播的慢变包络振幅，βi表示第i阶模的传播常数。

在长周期光子晶体光纤光栅中假设:(1)在纤芯区域只存在基波导模;(2)忽略纤芯各纵向模耦合系数;(3)忽略各包层模之间的耦合;(4)忽略各轴向模间的耦合。在上述假设条件下，参考模式耦合共振条件，根据耦合模理论，推导得到长周期光子晶体光纤光栅谐振波长表示为［4］:

式中，Δn为折射率波动量。

对于弯曲长周期光子晶体光纤光栅，在(4)式中只考虑弯曲应变造成光栅波长漂移，其它因素不考虑，对(5)式中以应变为自变量进行Taylor级数零点展开，如光栅形变属于弹性形变，形变量与光栅长度相比较足够小，保留Taylor展开式中的一次项，并根据弹光理论可得:

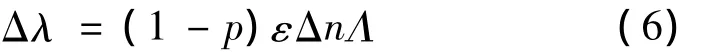
(6)式表征了弯曲长周期光子晶体光纤光栅谐振波长的漂移量与PCF光栅的应变ε，PCF光栅材料结构和PCF横向折射率的分布间关系。其中，p=neff2×［p12-γ(p11-p12)］/2，式中，neff为光纤有效折射率，p11和p12为光纤的弹光系数，γ为光纤材料泊松比，Δn指一个光栅周期里折射率的改变。在弯曲长周期光子晶体光纤光栅中折射率分布可通过下式计算［4］:

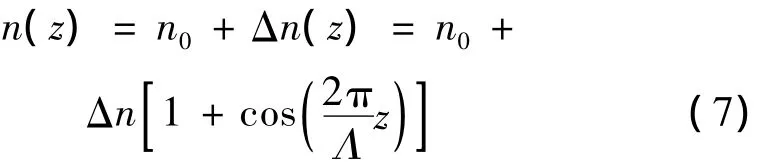
式中，n0指纤芯纯硅折射率，一般而言，Δn≪n0。

2 弯曲长周期光子晶体光纤光栅传感器设计

本文中给出的光子晶体光纤结构如图1a所示。光子晶体光纤纤芯是实芯，周围由空气孔六角周期排列而成。长周期光子晶体光纤光栅结构如图1b所示，折射率的扰动沿光栅的长度方向。

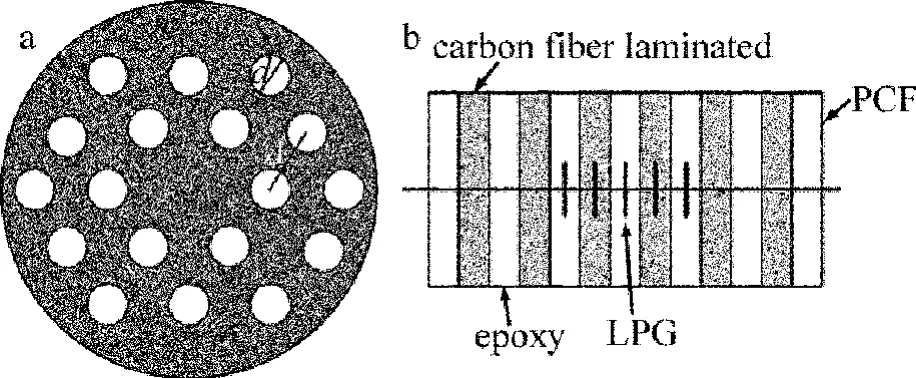
Fig.1 a—sectional view of photonic crystal fiber b—structure diagram of photonic crystal fiber grating

在外界参量作用下，长周期光子晶体光纤光栅产生形变，发生弯曲，弯曲示意图如图2所示。长周期光子晶体光纤光栅置于一个固定装置上，如图3所示。在图2中，L为长周期光子晶体光纤光栅的长度，h表示长周期光子晶体光纤光栅横向弯曲量，R表示长周期光子晶体光纤光栅弯曲而形成的曲率半径。根据图2，当长周期光子晶体光纤光栅发生弯曲时，弯曲曲率可表示为［8］:

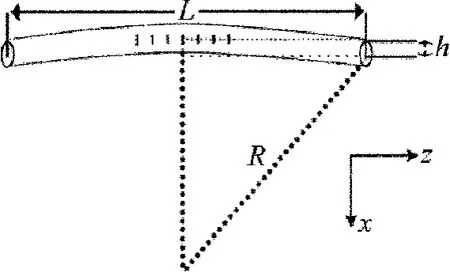
Fig.2 Diagram of long period bending photonic crystal fiber grating

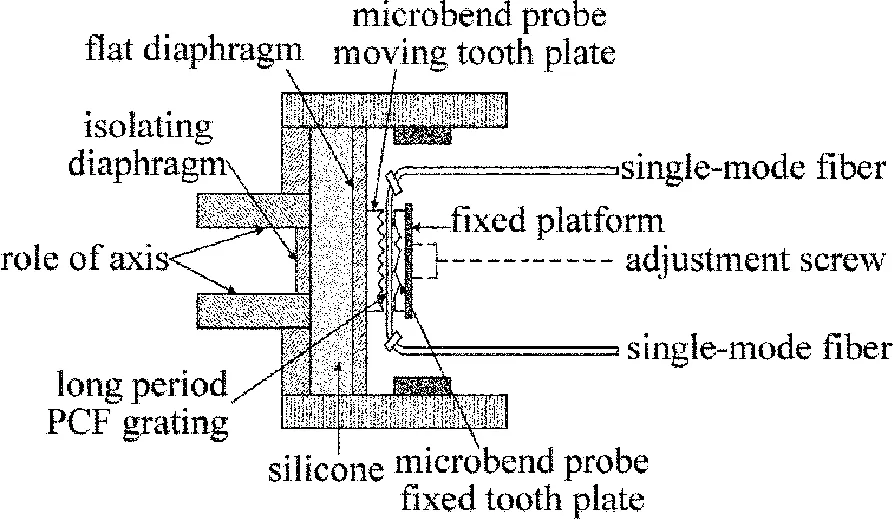
Fig.3 Structure of long period bending photonic crystal fiber grating sensor

对(8)式进行微分，可得长周期光子晶体光纤光栅弯曲曲率半径增量与光栅纵向和横向应变的关系如下式所示:

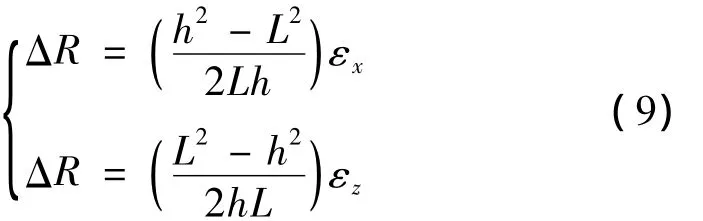
式中，εx=Δh/h表示光栅横向弯曲应变，εz=ΔL/L表示光栅长度方向应变，把(9)式纵向应变和横向应变代入(6)式，得到长周期光子晶体光纤光栅传感器的谐振峰波长的漂移量与弯曲曲率半径的函数关系。

根据图1中的PCF结构和长周期光子晶体光纤光栅的参量，本文中设计了一种长周期光子晶体光纤光栅弯曲传感器系统，系统结构如图3所示。

在图3中，敏感元件长周期光子晶体光纤光栅位于导入和导出单模光纤之间。光脉冲经过导入光纤进入长周期光子晶体光纤光栅，因为外力作用通过硅油传递到长周期光子晶体光纤光栅上，外界作用改变了光栅的形变和弯曲，传播的光脉冲谐振波长和传播相位发生改变，作用后的光脉冲通过导出光纤传输至长周期光子晶体光纤光栅传感器测量系统设备。

3 弯曲长周期光子晶体光纤光栅传感器数值分析

图3的弯曲长周期光子晶体光纤光栅传感器系统中，敏感元件长周期光子晶体光纤光栅PCF如图1a所示，长周期光子晶体光纤中光栅如图1b所示。对于所设计长周期光子晶体光纤光栅传感器系统进行如下假设:(1)PCF长周期光栅折射率改变沿PCF纵向对称周期性分布;(2)在PCF横向结构中，折射率沿各个方向是均匀分布;(3)纤芯基模谐振耦合进LP11包层模;(4)PCF长周期光栅圆形弯曲，其结构如图2所示。根据上面的假设则弯曲PCF等价折射率分布可采用下式定义:

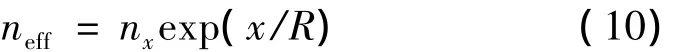
式中，nx表示光子晶体光纤光栅折射率横向分布，x表示光栅横向偏离中心处位置，R为长周期光子晶体光纤光栅弯曲半径。把(8)式代入(10)式可得:

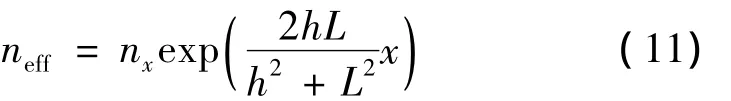
把(11)式代入(6)式可得长周期光子晶体光纤光栅在弯曲应变情况下谐振中心波长的漂移量表达式:

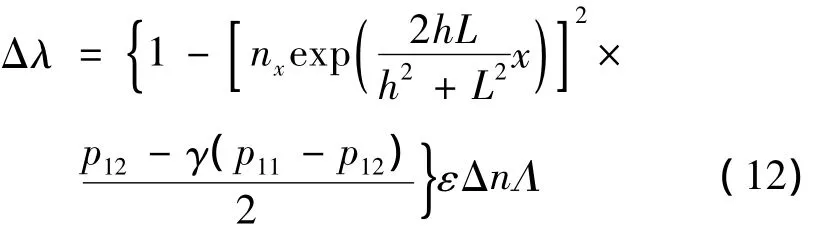
设光栅长度L=50mm，调节图3中作用轴使长周期光子晶体光纤光栅发生弯曲，其弯曲量h取值0mm～5mm，长周期光子晶体光纤光栅的曲率变化如图4所示。

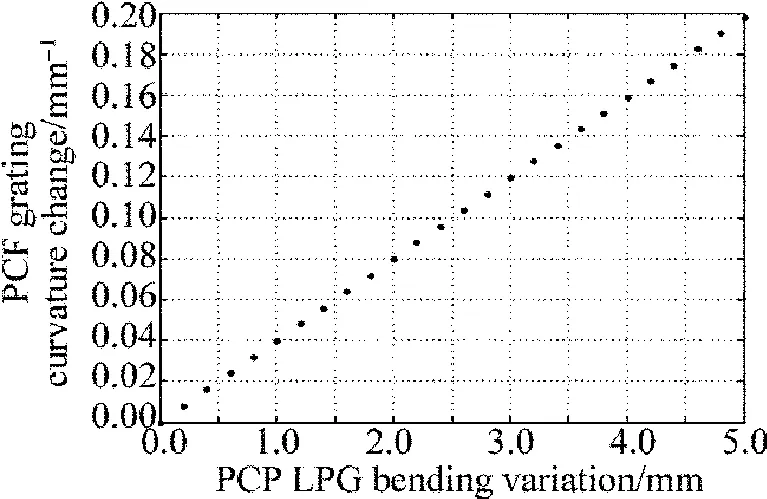
Fig.4 Relationship between curvature change and bending variation of long period photonic crystal fiber gratings

图4 表明，长周期光子晶体光纤光栅的曲率变化与弯曲h的变化关系近似线性关系，这个结果与(7)式的理论预期结果是一致的，在(7)式中，当h≪L时，曲率1/R与h可认为是线性的。

PCF纤芯折射率取值1.465，长周期光子晶体光纤光栅弯曲值从3mm至6mm，取PCF纤芯中心处为零点，可计算得到长周期光子晶体光纤光栅有效折射率横向分布与x的关系，结果如图5和图6所示。

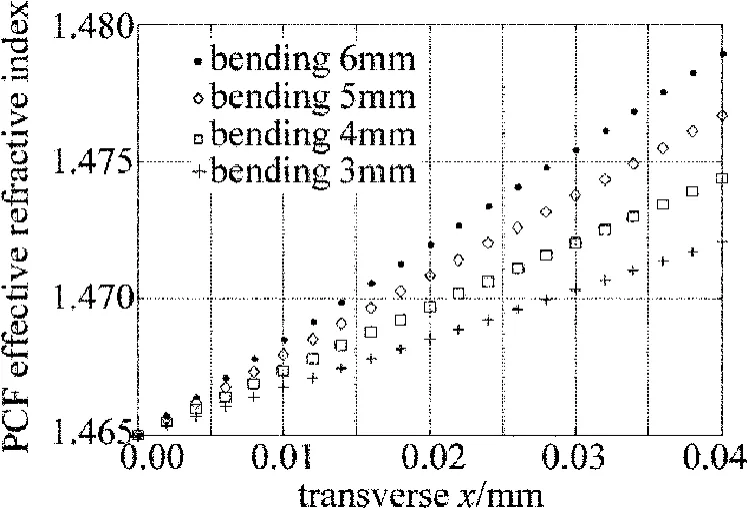
Fig.5 Relationship between the transverse distribution of effective refractive index and the transverse position x in the core of long period bending photonic crystal fiber grating

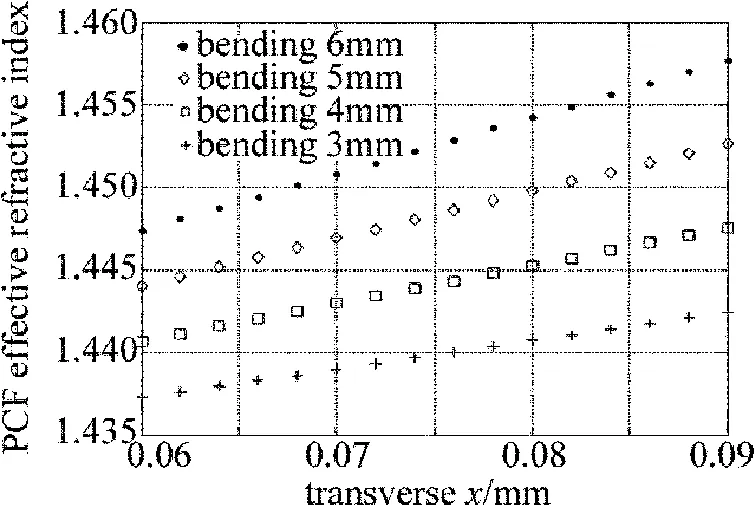
Fig.6 Relationship between the transverse distribution of effective refractive index and the transverse position x in the clad of long period bending photonic crystal fiber grating

图5 表示光栅纤芯处有效折射率与横向位置x的关系。纤芯是实芯，由纯硅构成。图5表明，光栅纤芯有效折射率随x的增加也会增加，在同一x处，有效折射率会随弯曲量的增加而增加，离中心处越远，这个增加量会变大。

图6表示包层的有效折射率随横向点x的变化关系。包层由空气孔和硅周期组成，其有效折射率会低于纤芯处。图6表明，当弯曲发生时，其对于同一弯曲程度，离中心越远，光栅有效折射率会越大，在同一位置处，有效折射率也会随弯曲程度的增加而增加。

在图3中，因为作用轴的作用，长周期光子晶体光纤光栅会发生弯曲，这个弯曲会使光栅的横向和纵向产生应变，因为应变，光栅的曲率会产生改变。其曲率改变量与应变的关系如图7和图8所示。

从图7可知，在弯曲程度相同情形下，随着长周期光子晶体光纤光栅横向应变的增加，光栅的弯曲半径也会增加，而在相同应变的情况下，随着光栅弯曲程度的增加，而光栅弯曲半径的增加量反而会减少。在图7中弯曲半径的增加量值是一个负值，这表明随着横向应变的增加，弯曲发生与作者所取的正方向相反。

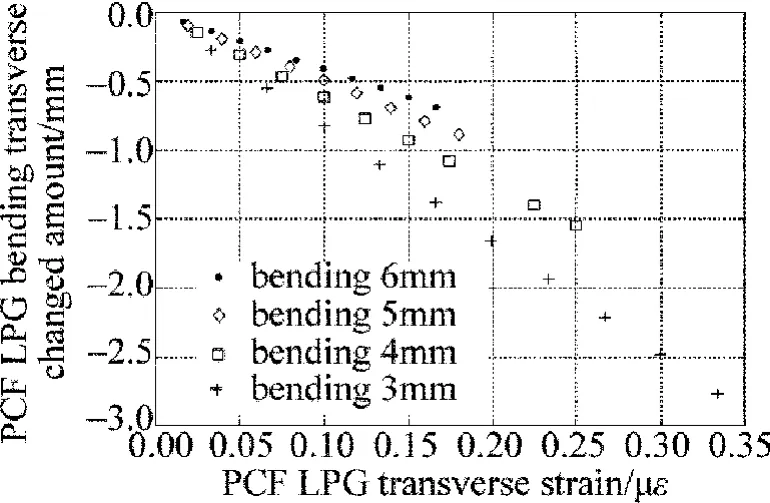
Fig.7 Relationship between the transverse strain change and the grating bending radius change in long period bending photonic crystal fiber gratings

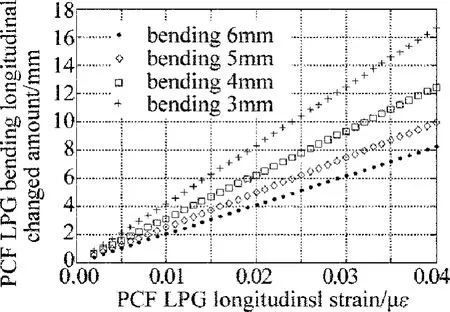
Fig.8 Relationship between the longitudinal strain change and the grating bending radius change in long period bending photonic crystal fiber gratings

图8 表示当长周期光子晶体光纤光栅产生纵向应变时，光栅弯曲半径变化量与纵向应变的关系。根据图8可知，当光栅的弯曲一定时，随着纵向应变的增加，弯曲半径也会增加，而在纵向应变相同时，弯曲程度越大，光栅弯曲半径的增加量会减少，也即光栅弯曲曲率会增加量会变得更大。

在(11)式中取值如下，PCF的弹光系数 p11=0．12，p12=0.27，PCF的 Poisson 系数 ν=0.17，纤芯处PCF折射率取值1.465，而包层有效折射率取值1.437，作出长周期光子晶体光纤光栅谐振波长的漂移量与光栅周期和光栅应变的关系如图9和图10所示。

在图9中，如果长周期光子晶体光纤光栅的周期

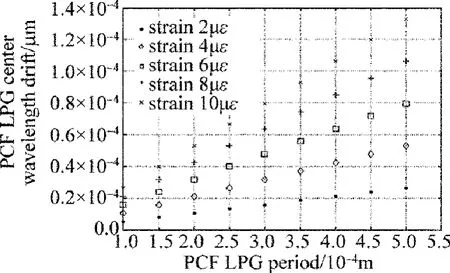
Fig.9 Relationship between the resonance wavelength drift and the grating period in long period bending photonic crystal fiber gratings

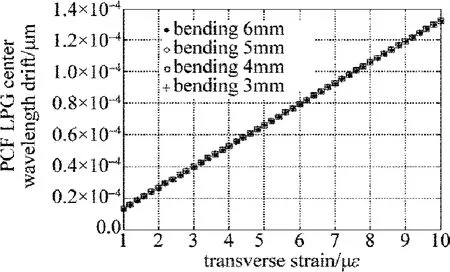
Fig.10 Relationship between the resonance wavelength drift and the grating strain in long period bending photonic crystal fiber gratings

不变，则随着光栅应变的增加谐振波长的漂移量会增加，应变每增加2με，中心波长漂移量增加大约0.01nm，而光栅如果应变保持相同值，则光栅谐振波长的漂移量会随着长周期光子晶体光纤光栅周期的增加而增加，光栅周期每增加50μm，中心波长漂移量增加大约0.005nm。

图10表征了当光栅发生弯曲时，长周期光子晶体光纤光栅谐振波长的漂移量与光栅应变的关系，在图10中，在相同应变情况下，光栅的弯曲程度对光栅谐振波长的漂移量影响非常小，而对于同一弯曲情形，光栅应变的增加对光栅谐振波长的漂移量影响较大，光栅每发生1με变化，光栅谐振波长的漂移量变化0.014nm。

4 结论

光子晶体光纤光栅是一种新型无源材料，具有许多独特的传光特性，在光纤通信和光纤传感中具有特殊应用，而弯曲长周期光子晶体光纤光栅在道路、桥梁及建筑健康检测中有非常重要的应用。根据本文中的分析，光栅的谐振波长漂移量与光栅的形变、长周期光子晶体光纤光栅材料的具体构建都相关联，长周期光子晶体光纤光栅弯曲会造成光栅折射率分布、横向和纵向应变发生变化，并最终导致长周期光子晶体光纤光栅的谐振波长漂移，通过检测谐振波长的漂移量就可以检测出长周期光子晶体光纤光栅的弯曲程度。

［1］ KUTZ J N，EGGLETON B J，STARK J B，et al.Nonlinear pulse propagation in long period fiber gratings:theory and experiment［J］.IEEE Journal of Selected Topics in Quantum Electronics，1997，3(5):1232-1244.

［2］ HE D D，LIU M，JIAN D，et al.Study on loss in hollow-core photonic bandgap fibers［J］.Laser Technology，2013，37(2):243-246(in Chinese).

［3］ LIU Z H，ZHENG Y.Experimental study about the cavity of Yb3+-doped photonic crystal fiber laser［J］.Laser Technology，2014，38(1):105-108(in Chinese).

［4］ YU X，SHUM P，REN G B.Highly sensitive photonic crystal fiberbased refractive index sensing using mechanical long-period grating［J］.IEEE Photonics Technology Letters，2008，20(17):1688-1690.

［5］ DENG M，SUN X K，WEI H F，et al.photonic crystal fiber-based modal interferometer for refractive index sensing［J］.IEEE Photonics Technology Letters，2014，26(6):531-534.

［6］ WEN K，PENG H，WANG J Y，et al．Finite element analysis of a novel weak-pressure sensor based on fiber Bragg grating in photonic crystal fibers［J］.Optical Engineering，2009，48(3):034402.

［7］ JIN L，JIN W，JU J.Directional bend sensing with a CO2-laser-inscribed long period grating in a photonic crystal fiber［J］.Journal of Lightwave Technology，2009，27(21):4884-4891.

［8］ WANG Y P，RAO Y J.A novel long period fiber grating sensor measuring curvature and determining bend-direction simultaneously［J］.IEEE Sensors Journal，2005，5(5):839-843.

［9］ SHAO L Y，XIONG L Y，CHEN Ch K，et al.Directional bend sensor based on re-grown tilted fiber Bragg grating［J］.Journal of Lightwave Technology，2010，28(18):2681-2687.