YAG激光晶体热致双折射的非线性分析

田　佳，胡　健，王　珂，王海林，朱长虹，朱广志，齐丽君，朱　晓*

(1.华中科技大学 光学与电子信息学院，武汉 430074; 2. 华中科技大学 激光加工国家工程研究中心，武汉 430074)

YAG激光晶体热致双折射的非线性分析

田佳1,2，胡健1,2，王珂1,2，王海林1,2，朱长虹1,2，朱广志1,2，齐丽君1,2，朱晓1,2*

(1.华中科技大学 光学与电子信息学院，武汉 430074; 2. 华中科技大学 激光加工国家工程研究中心，武汉 430074)

摘要：为了克服线性模型在描述高功率运转的激光晶体时，热焦距和热致双折射计算值与实测值不符的缺点，采用非线性热传导模型，计算了常用[111]切割方向Nd∶YAG激光晶体的热致双折射椭圆分布以及径向和切向热焦距。进行了平均热焦距数据测量和旋转线偏振光干涉实验，实验结果与理论分析吻合。结果表明，非线性模型对Nd∶YAG激光晶体在高功率运转时的描述更符合实际情况，普适性更强。这一结果对于设计高功率径向或切向偏振固体激光器是有帮助的。

关键词：非线性光学; 热致双折射; 旋转线偏振光干涉; Nd∶YAG激光晶体

文章编号：1001-3806(2015)04-0520-05

中图分类号：TN244

文献标志码：志码：A

doi:10.7510/jgjs.issn.1001-3806.2015.04.020

Abstract：To overcome the shortage of mismatch of the calculated value and the measured value of thermal induced birefringence and thermal focal length when applying linear heat conduction model to describe a laser crystal operating in high power, based on nonlinear heat conduction model analysis, the distribution of the thermal induced birefringence ellipse and the radial or tangential thermal focal length in a Nd∶YAG laser crystal of common [111]-cut were analyzed. The average thermal focal length data and rotated interference pattern of linearly polarized light were measured. The experimental results fit the theoretical analysis. The results show that nonlinear model provides more realistic and more general description for an Nd∶YAG laser crystal in [111]-cut. The result is helpful for the design of radial or tangential polarized high power solid-state lasers.

作者简介：田佳(1989-)，男，硕士研究生，现主要从事高功率固体激光器的研究。

收稿日期：2014-06-09；收到修改稿日期：2014-07-17

Nonlinear analysis of thermal induced birefringence of YAG laser crystal

TIANJia1,2,HUJian1,2,WANGKe1,2,WANGHailin1,2,ZHUChanghong1,2,

ZHUGuangzhi1,2,QILijun1,2,ZHUXiao1,2

(1.School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China; 2. National Engineering Research Center for Laser Processing, Huazhong University of Science and Technology, Wuhan 430074, China)

Key words:nonlinear optics; thermal induced birefringence; rotated interference of linearly polarized light; Nd∶YAG laser crystal

*通讯联系人。E-mail:zx@mail.hust.edu.cn

引言

固体激光器在高功率运行时，激光晶体内部会形成大温度梯度和热应力，热效应严重制约了激光晶体抽运功率密度的提高，降低了光束质量和输出功率，并导致产生热退偏效应[1-2]。近年来，径向和切向偏振激光器已获得广泛关注，并且在工业加工中有重要的应用潜力[3-4]，因此，对高功率Nd∶YAG激光晶体的热致双折射特性分析具有重要研究意义。

棒状Nd∶YAG激光晶体横截面内的传统稳态热传导模型(下面简称为线性模型)，导热率为定值κ0=13.6W/(m·K)。线性模型计算的热屈光度与抽运功率Pin呈线性关系，而热屈光度实测值与Pin的非线性关系已被大量的实验所证明[5-6]；另外，基于线性模型的晶体热破裂应力理论值也要高于实测值[7]。针对线性模型存在的不足，俄罗斯极地所ROZANOV[8]提出了非线性稳态热传导模型(下面简称为非线性模型)，并进行了热致折射率变化的研究以及热应力的计算，但对于Nd∶YAG激光晶体的热致双折射和偏振特性的分析尚未涉及。固体激光器在强抽运、高平均功率条件下运转时，热致双折射对径向和切向热焦距以及偏振特性有直接而重要的作用，而近年来针对热致双折射的分析仍基于线性模型[9-10]，因此作者针对常用[111]切割方向的Nd∶YAG激光晶体，在非线性模型基础上进行热致双折射和偏振特性的研究与分析。

1非线性模型分析

在非线性模型中，导热率κ(T)随温度的增大而减小，设横向均匀抽运且无纵向温差，柱坐标系下Nd∶YAG激光晶体横截面内稳态热传导方程为[8]：

式中，r为径向坐标，T为绝对温度，κ(T)=γ/T。室温为293K时，导热率的测量值κ0=13.6W/(m·K)，由此得出系数γ=3980W/m，Q=ηPin/(πr02L)表示单位体积的均匀发热量，Pin为抽运功率，η为发热效率，r0为激光晶体半径，L为激光晶体长度。对(1)式整理得：

(2)式在满足边界条件r=r0，T(r0)为激光晶体表面温度时，有精确的解析解：

精确解进行指数项展开，前两项即为基于线性模型计算得到的温度分布[11]。整理(3)式得：

其非线性不仅体现在包含r2的exp[-Qr2/(4γ)]项，还体现在仅与Pin相关的指数项exp[-Qr02/(4γ)]，非线性效应随Pin的增加呈指数增加。

1.1　热致双折射计算

常用[111]切割方向Nd∶YAG激光晶体，根据弹光理论，可以先由激光晶体横截面的温度分布得到应力或应变分布(柱坐标系下)，然后在统一的坐标系下，根据光弹矩阵张量计算得到径向和切向折射率变化量。目前较好的方法有两种，方法一[12]是将直角坐标系下激光晶体的光弹矩阵变换到柱坐标系下，再与应力或应变计算；方法二[9]是将应力或应变分布变换到直角坐标系下，与直角坐标系下激光晶体的光弹矩阵计算。非线性模型下的应力或应变表达式更为复杂，进行坐标变换繁琐，故选择方法一来计算垂直于激光晶体通光横截面的径向和切向的折射率差：

式中，nr和nφ分别为Nd∶YAG激光晶体径向、切向折射率，n0=1.82为Nd∶YAG激光晶体“冷”折射率，A=αEn03T(r0)/[2(1-ν)]，线膨胀系数α=7.8×10-6K-1，杨氏模量E=3.17×1011N/m2，泊松比ν=0.3，应力光弹π张量矩阵系数π11=0.30285×10-12m2·N-1,π12=+0.11158×10-12m2·N-1,π13=+0.17187×10-12m2·N-1。

分析(5)式、(6)式可以得到[111]切割方向激光晶体横截面内热致双折射率椭圆的分布示意图，如图1所示。将晶格方向[101]与极轴X重叠，晶格方向[121]Y轴，具体分布规律见下。

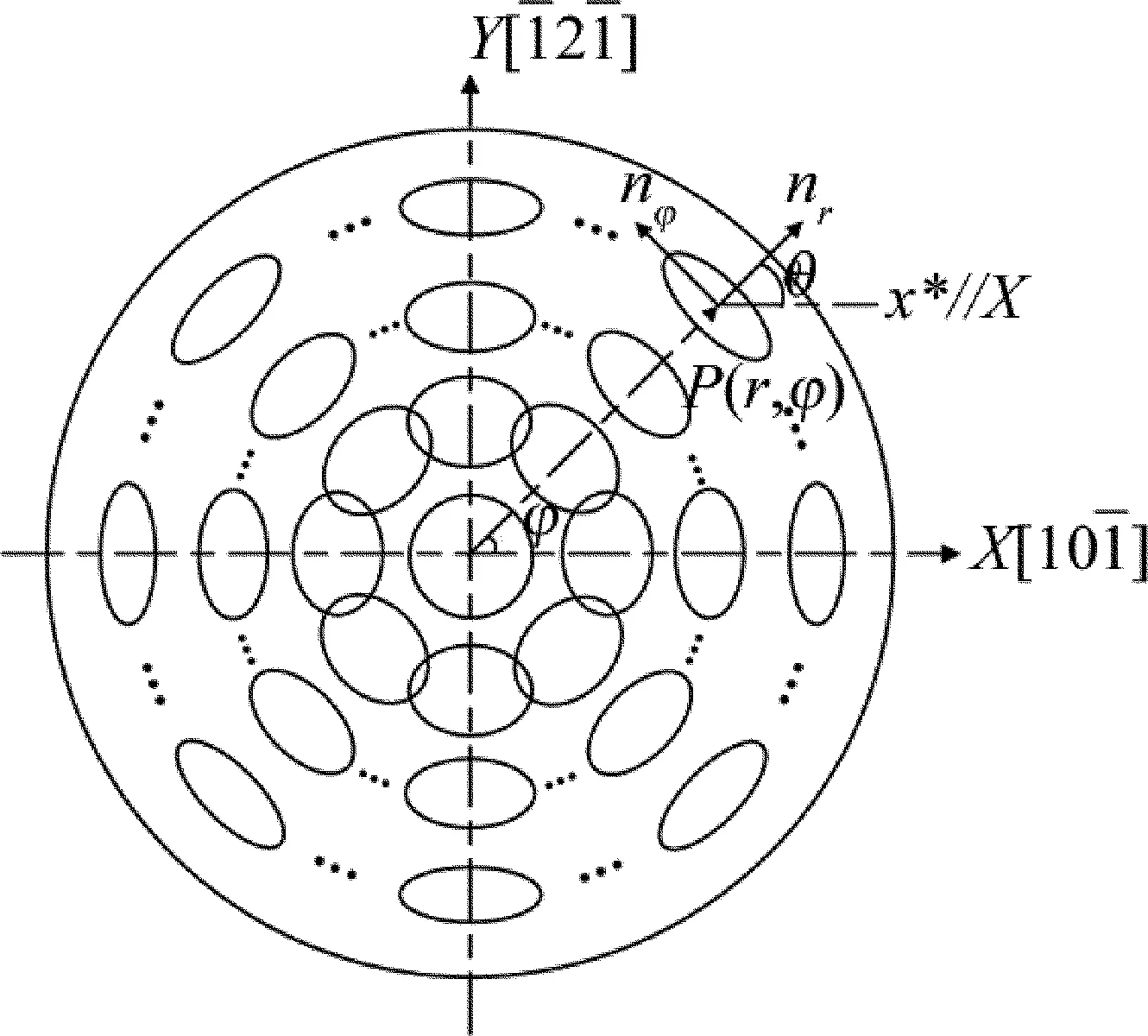
Fig.1DistributiondiagramofthermalinducedbirefringenceellipseinNd∶YAGlasercrystalcross-sectionof[111]-cut

(1)激光晶体横截面中，热致双折射率椭圆呈径向对称分布，与极坐标角度φ无关，任意一点P(r, φ)热致双折射率椭圆的主轴nr与X轴的夹角θ始终存在关系tan(2θ)=tan(2φ)[9,13]。

(2)激光晶体横截面内任意一点P(r,φ)热致双折射率椭圆的两主轴分别与该点径向和切向方向共线(长轴与切向方向共线、短轴与径向方向共线)，根据非线性模型计算长轴长度始终大于短轴长度(切向折射率始终大于径向折射率)。

光波电场径向和切向的相位差与径向和切向折射率差呈正比例关系δ∝(nr-nφ)，因此径向相对于切向产生相位延迟，中心相位差趋近于0。图1为光波电场径向和切向的相位差为旋转偏振光干涉实验提供了理论基础。

1.2　径向和切向热焦距计算

热焦距由热透镜效应引起，热透镜效应源自于折射率变化以及端面效应产生的形变，端面效应对热焦距贡献不超过6%，因此本文中忽略端面效应的影响。折射率变化包括激光晶体内部温度梯度导致的折射率差和热致双折射导致的折射率差，激光晶体内部非线性模型温度梯度导致的折射率差为：

式中，折射率温度系数dn/dT=7.3×10-6K-1。[111]切割方向Nd∶YAG激光晶体基于非线性模型的热焦距计算，首先将(5)式、(6)式和(7)式中仅与Pin相关的非线性项exp(Qr02/4γ)保留，再将指数项exp[-Qr2/(4γ)]进行类透镜近似[3]，展开至r2项：

式中，C2r=-π11+π22，C2φ=π11-π22，C3r=π12+π13，C3φ=π11+π13。因此[111]切割方向Nd∶YAG激光晶体的径向、切向热焦距为：

采用(5)式、(6)式中的相同参量计算切向与径向热焦距的比值为1.32，与实测值1.23~1.5[5]的均值1.365相近，精度高于线性模型的计算值1.2[11]，同时也证明热致双折射理论分析得到径向和切向折射率差关系Δnφ>Δnr>0，nφ>nr>n0的准确性，从而可确定热致双折射椭圆的径向主轴长度短于切向主轴长度。准确计算径向和切向热焦距的差异，是设计径向或切向线偏振激光器的基础[14]。

2实验结果分析

为验证非线性模型分析方法的正确性，进行了[111]切割方向Nd∶YAG激光晶体热焦距测量以及旋转偏振光干涉实验，实验中采用双氙灯抽运的Nd∶YAG激光晶体，尺寸为∅7mm×150mm。

2.1　热焦距测量实验

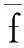
Fig.2Comparisonbetweenthecalculatedandmeasuredvalueofaveragethermaldiopter

2.2　旋转线偏振光干涉实验

从图1分析得出，在激光晶体横截面中热致双折射率椭圆呈径向对称分布，与极坐标角度φ无关，X-Y轴并不代表特殊方向，做旋转偏振光实验时，中心黑十字区域应该同步旋转，针对此设计思路设计Nd∶YAG晶体偏光干涉实验装置,如图3所示，在[111]切割方向激光晶体两端放置偏振方向相互正交的偏振片P1和P2，设实验室坐标系中水平方向为x轴，竖直方向为y轴，同时取x轴方向为激光晶体横截面所在极坐标系φ=0的极轴方向。使用He-Ne激光作为探测光源，经准直扩束后可以充满激光晶体截面。

激光晶体横截面内的角度示意图如图4所示，P(r, φ)为激光晶体横截面中任意一点，θ为热致双折射椭圆的主轴nr与x轴夹角，τ为入射偏振光E与x轴夹角，β为入射偏振光E与y轴夹角，τ+β=π/2。

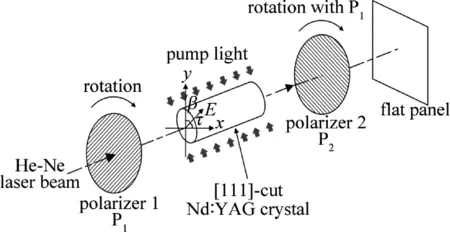
Fig.3Experimentalsetuptomeasuretherotatedinterferenceoflinearlypolarizedlight

Fig.4DistributiondiagramoftheangleinNd∶YAGlasercrystalcross-sectionof[111]-cut

He-Ne激光器发出的探测光束，通过P1成为线偏振光，再依次通过激光晶体和P2，若Nd∶YAG激光晶体没有抽运的情况下，立方晶系光率体为圆形，正交偏振片可以完全消光，接收屏上没有干涉图样产生；若激光晶体在抽运光作用下产生热致双折射，不在热致双折射椭圆主轴方向上的线偏振光其偏振态将发生变化，在接收屏上产生干涉条纹。同步转动P1和P2，使β在[0, 2π]内连续变化，干涉条纹以π/2为周期连续变化。设Nd∶YAG激光晶体的输入探测光光强为I0，输出干涉光强分布为[9]：

低抽运功率为6kW时，由于篇幅有限，取干涉条纹一个变化周期内的部分干涉图(如图5所示)进行分析：干涉图由黑色十字和明暗等差线圈组成，黑色十字是由两相互垂直的黑色区域组成，并伴随偏振片同步转动；此干涉图与负单轴晶偏振光干涉图样类似。

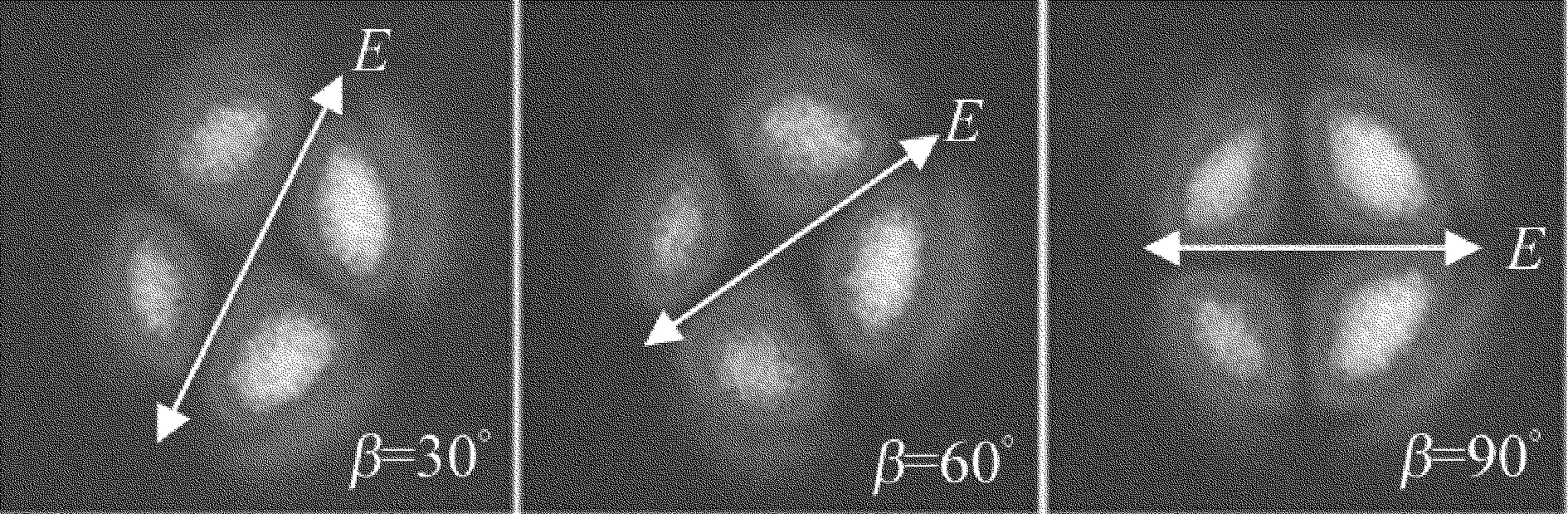
Fig.5Rotated interference patterns of linearly polarized light of a [111]-cut Nd∶YAG laser crystal in 6kW pump power

高抽运功率为12kW时，同样取干涉条纹一个变化周期内的部分干涉图(如图6所示)进行分析，干涉图与低抽运功率时的干涉图结构相近，唯一区别在于干涉条纹的旁瓣数增加，这是由于高抽运功率增强了热致双折射效应，激光晶体边缘处的热致双折射强于中心处，因此,较强的热退偏效应使边缘处的干涉条纹更加密集。

Fig.6Rotated interference patterns of linearly polarized light of [111]-cut Nd∶YAG laser crystal in 12kW pump power

对于[111]切割方向Nd∶YAG激光晶体，综合图1所示热致双折射椭圆分布图和图5、图6所示旋转偏振光干涉实验现象分析可得：(1)激光晶体横截面中心为各向同性区，光率体为圆，偏振方向正交的两偏振片可完全消光；(2)当任意方向(如图7中E方向)的线偏振光入射到激光晶体横截面，总可以找到折射率椭圆主轴与偏振光方向共线的两个方向(如图7中p1方向和p2方向，p1方向上E∥nr，p2方向上E∥nφ)，在这两个方向上热致双折射只会导致线偏振光的相位变化，不改变偏振状态，经过P2之后，在接收屏上形成黑色十字区域；(3)折射率椭圆主轴与偏振光方向非共线的任意方向(如图7中除p1和p2方向之外的所有方向)，每一点处的热致双折射椭圆主轴与偏振光方向存在夹角，线偏振光在两主轴上的分量有相位差δ，因此会改变偏振状态，经过P2后，在接收板上黑色十字区域之外形成干涉条纹；(4)当P1和P2同步旋转，即β在[0,2π]内连续变化时，会与对应的不同角度φ上热致双折射椭圆的主轴重合，黑色十字区域会伴随偏振片的旋转角度β而旋转，但干涉图结构并没有发生改变，仅以黑色十字的交叉点为对称中心进行旋转，也证明了[111]切割方向Nd∶YAG激光晶体横截面内的热致双折射椭圆呈径向对称分布，没有特殊方向。

Fig.7Formation diagram of black cross region in the rotated interference patterns of linearly polarized light (1/2 laser crystal cross-section)

参考文献若按照[11]中的描述，即如图8所示，在旋转偏振光实验中，P1和P2同步旋转角度时，无论β取值如何，干涉图中会有一个黑色十字固定出现在x轴、y轴所在的特殊方位，因为该区域光率体为圆，所以两偏振方向正交的偏振片可以完全消光。这一推论与实验结果中黑色十字同步旋转的现象相悖，因此图8不是[111]切割方向Nd∶YAG激光晶体横截面内热致双折射率椭圆的分布示意图，特别指出这一点，避免学术界和工程界的错误引用。

Fig.8　Schematic diagram of reference [11]

3结论

针对强抽运、高功率固体激光器，基于非线性模型，进行了[111]切割方向Nd∶YAG激光晶体热致双折射与偏振特性的研究。得出了[111]切割方向Nd∶YAG激光晶体纵向截面内热效应作用下的热致双折射椭圆分布图，通过偏振光干涉实验证明了[111]切割方向激光晶体内热致双折射椭球的分布仅与半径相关与角度无关的结论，并详细解释了实验中黑色十字区域旋转的原理。基于非线性模型重新分析了[111]切割方向Nd∶YAG激光晶体热焦距，理论值与实测值的吻合度较线性模型更高。研究结果对高功率径向或切向偏振棒状固体激光器的设计具有参考意义。

[1]TÜNERMANN H, PUNCKEN O, WEBLS P,etal. Linearly polarized single-mode Nd∶YAG oscillators using [100]- and [110]-cut crystals[J]. Optics Express, 2011, 19(14): 12992-12999.

[2]GAO J C, ZHU C H, LI Z J. Study on the thermal effect and the optical pump limit about solid state laser medium[J]. Laser Technology, 2004, 28(3): 271-274 (in Chinese).

[3]YU Z S, LIU J, LIU J,etal. Study of the distributed thermal lens of LD end pumped rectangular gain[J]. Optics Express, 2013, 21(20): 23197-23205.

[4]LUMER Y, MOSHE I. Radial and azimuthal beam parameters[J]. Optics Letters, 2009, 34(3):265-267.

[5]MAcHAVARIANI G, LUMER Y, MOSHE I,etal. Birefringence-induced bifocusing for selection of radially or azimuthally polarized laser modes[J]. Applied Optics, 2007, 46(16): 3304-3310.

[6]MOSHE I, JACKEL S. Influence of birefringence-induced bifocusing on optical beams[J]. Journal of the Optical Society of America,2005, B22(6): 1228-1235.

[7]ZVEREV G M. Materials for use in quantum electronics-yttrium-aluminum garnet, lithium niobate[J]. Akademiia Nauk SSSR Izvestiia Seriia Fizicheskaia, 1980, 44(1): 1614-1621.

[8]ROZANOV A G. Nonlinear model of thermal effects in YAG∶Nd laser crystals[J]. Soviet Journal of Quantum Electronics, 1991, 21(10): 1074-1076.

[9]PUNCKEN O, TÜNERMANN H, MOREHEAD J J,etal. Intrinsic reduction of the depolarization in Nd∶YAG crystals[J]. Optics Express, 2010, 18(19): 20461-20474.

[10]LUMER Y, MOSHE I, JACKEL S,etal. Depolarization induced by pump edge effects in high average power laser rods[J]. Journal of the Optical Society of America, 2010, B27(1): 38-44.

[11]KOECHNER W. Solid-state laser engineering[M].5th ed. Beijing: Science Press, 2002: 356-370 (in Chinese).

[12]LÜ Q, WITTROCK U, DONG S. Photoelastic effects in Nd∶YAG rod and slab lasers[J]. Optics & Laser Technology, 1995, 27(2): 95-101.

[13]SHOJI I, TAIRA T. Intrinsic reduction of the depolarization loss in solid-state lasers by use of a (110)-cut Y3Al5O12crystal[J]. Applied Physics Letters, 2002, 80(17): 3048-3050.

[14]LUMER Y, MOSHE I, HOROVITZ Z,etal. Thermally induced birefringence in nonsymmetrically pumped laser rods and its implications for attainment of good beam quality in high-power, radially polarized lasers[J]. Applied Optics, 2008, 47(21): 3886-3891.

[15]OU Q F, FENG G Y, LIU D P,etal. Simulation and experimental study on thermal effects of Nd∶YAG lasers[J]. Laser Technology, 2002, 26(1): 15-16 (in Chinese).