基于彩色数字全息的透镜焦距检测

王晓惠，刘 超，陆英仕，楼宇丽

(昆明理工大学理学院，昆明650500)

引 言

在光学无损检测领域中，全息技术是一种精密检测技术［1-5］。与传统全息相比，数字全息省去了底片处理的过程，大大节省了时间，由于缩短了曝光时间，从而降低了对振动的敏感性，可以定量地得到相位信息。数字全息的这些优点使它适合应用于物体3维形貌及微形变等物体量的测量［5-6］。实时数字全息检测研究中，测量物体表面微形变这一类物理量时，需要实时检测观测点不共面的3个位移矢量，通常使用3种不同波长的激光进行彩色数字全息检测。当被测量物体的投影尺寸与CCD面阵尺寸有较大差异时，为让CCD较好地接收物光场信息，采用光学系统对物光场进行变换是通常采取的措施。例如，让物光通过不同性质的透镜组成的显微镜或变焦系统［7-9］，将物体成像在CCD平面。然而，由于透镜的焦距是光波长的函数，当使用多种波长的光照射物体时，不同波长的光对应不同的像平面。因此，当光学系统给定后，准确确定不同波长光照射下物体的像平面，并通过数字全息重建不同色光的物体像，是应用研究中必须解决的问题。

当光学变换系统可以由四元素的光学矩阵描述时，将矩阵光学与衍射光学相结合，LI等人提出在像空间及物空间进行物光场重建的方法［7］。然而，当光学系统由多个光学元件组成时，必须准确知道每一光学元件的光学参量及构成光学系统时所在的准确位置。由于透镜是组成光学系统的主要元件，系统中所使用透镜的焦距值在重构图像时是一个重要参量，而透镜对不同波长的入射光有不同的焦距值，焦距值准确与否将直接影响到重构图像的质量好坏，因此透镜焦距的测量是很有必要的。虽然已有一些研究者进行过透镜焦距测量方面的工作［10-12］，但是均没有考虑焦距与入射光波长之间的关系。为此，作者提出简易可行的透镜焦距测量方法，对3种波长对应的焦距值进行了测定。给出了根据实测结果进行的彩色数字全息图像重建［13］的实例。

1 检测原理

实验原理如图1所示。

Fig.1 Diagram of interferometry

首先把从同一束激光分束，然后分别经过准直和扩束。其中通过待测透镜的透射光波为一球面波，该球面波与参考光波(也为一球面波)相遇后产生干涉，用CCD在干涉场中某一位置记录其干涉图像。通过对干涉条纹进行分析，测量出该位置的球面波波面半径d。d0为透镜到CCD间的距离，然后根据f=d0-d近似求出透镜焦距。以下给出CCD波面半径测量的理论分析。

干涉场强度为:

式中，λ为波长。令(x2+y2)=r2，则当相位差为时，出现干涉亮纹。

令n=m及m+1，对于两相亮纹，则由(2)式可得:

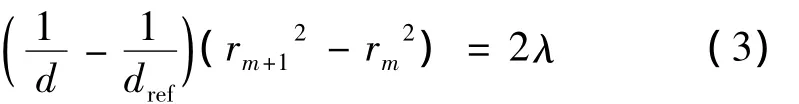
假设其中一个球面波的波面半径dref已知，则有:

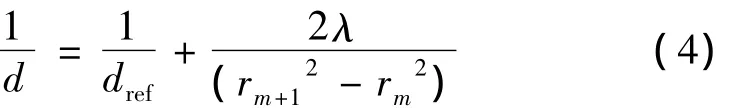
式中，rm+1和rm分别为相邻的第m+1级和第m级圆环的半径，和前面的处理一样，对上式进行整理，令Dm+1=2rm+1及Dm=2rm，得到下式:

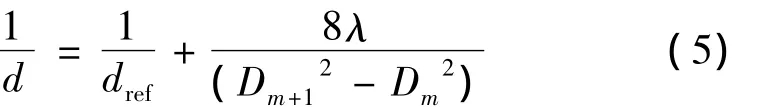
式中，dref可以直接测得。根据(4)式可以利用CCD测量的全息图上相邻两干涉环的直径来确定d。而d就是经待测透镜到达CCD接收面的球面波的波面半径，用(5)式多次测量的平均值为到达CCD的球面波的波面半径。则可计算出透镜焦距:f=d0-d，对于负透镜，f=d0-d为负值。

2 实验研究结果

2．1 数据处理

实验研究中，待测焦距的透镜是一个标称值为f0=-100mm的负透镜(该焦距的标称值是在587.6nm波长下测得)。本实验中用CCD记录了透镜后d0=385.0mm位置的透射光波与一球面参考波(波面半径dref=717.0mm)的干涉图像，该球面波的波面半径为每一位置分别采用了波长为0.0006328mm的红光、波长为0.000532mm的绿光及波长为0.000473mm的蓝光进行干涉实验。

Fig.2 Interference pattern under the irradiation of three wavelengthsa—red light interference pattern b—green light interference pattern c—blue light interference pattern

根据上面推导的(5)式编写程序，对实验中拍摄的3个干涉图进行处理后，求得到达CCD平面的3种色光的波面半径分别为:红光 dr=495.2mm，绿光dg=493.6mm，蓝光db=493.2mm。根据 f=d0-d，而d0=385.0mm，有:

2．2 透镜焦距的修正

从图1中可以看到，光束是经由一个分束镜才到达CCD平面进行干涉，分束镜的折射率与空气折射率间的差异，会对到达CCD平面的球面波波面半径的测量造成影响，为了准确测量透镜焦距，必须对直接由干涉图获取的波面半径进行修正。

根据光学理论，两点之间在距离不变情况下，若插入一折射率为n、厚度为t的透明介质，则光程的变化量为，实验中要据此进行修正。因为折射率与入射光的波长有关，所以要获取分束镜与各种色光对应的折射率。

对于本实验中使用的分束镜型号为DCL1010407(K9L)，材质为 H-K9L(517642)，厚度 t=25.4mm，其在587.6nm波长下的折射率为n=1．51680，根据插值公式 n2=a0+a1λ2+a2λ-2［9，14］，根据厂家提供的几种波长及对应折射率，由其中3种波长及对应折射率并利用n2=a0+a1λ2+a2λ-2就可计算出3个系数，分别为:a0=2．261，a1=1.459 ×10-2μm2，a2=-2.944 ×10-4μm4。对于每一种光波，就可据上式得到其对应的折射率。获得红光nr=1.51509，绿光ng=1.51947，蓝光nb=1.52336，很明显，折射率随光波长的增大而减小。

透镜的焦距与入射光的波长相关，根据参考文献［15］中的研究结果，不同色光照射下透镜焦距值间有关系式:

根据该式，如果知道透镜与某一光波对应的焦距值及折射率，只要知道与另一光波对应的折射率就可求出相应的焦距值。

已知透镜焦距标称值f0=-100mm(在587.6nm波长下测得，对应折射率为n=1.51680)为已知量，利用(7)式计算3种色光对应的焦距值。已知透镜材质为K9L系列玻璃，故利用前面的讨论，可知其对3种色光的折射率分别为:nr=1.51509，ng=1.51947，nb=1.52336。则3种色光干涉下对应的焦距值分别为:

由实验测得的结果与标称值间的相对误差均在1%左右;由实验测得的结果与理论获得的透镜焦距值相对误差虽然也在1%左右，但实验的结果与理论计算值均符合透镜焦距随入射光波长增大而增大的规律。

为进一步通过实验验证测量结果，在彩色数字全息波前重建实验中，分别将透镜焦距标称值和测量值作为参量代入，进行对比。

2．3 彩色数字全息波前重建实验

图3是记录数字全息图的简化光路。物体是105mm×75mm的泥塑彩绘猴王头像，在激光照射下，散射光通过凹透镜L0及分束镜Ms到达CCD形成物光，其与到达CCD的参考光进行干涉。分别用λ=0.0006328mm，λ =0.000532mm，λ =0.000473mm 3种色光进行干涉实验，拍摄全息图。

Fig.3 Simplified light path of digital hologram recording

实验中，由分束镜Ms上方引入的参考光是均匀球面波，通过实验调整参考光倾角，使得物体在像空间的快速傅里计变换重建像能与0级衍射光的干扰有效分离。相关的实验参量为:d0=220mm，d1=406mm，d2=25mm，d3=100mm。CCD面阵有效像素为1024×1024，物理宽度L=4.76mm。

基于参考文献［7］中提出的像空间重建的基本思想，将物体在像空间的像视为像空间进行波前重建的物体，将像到CCD的距离视为物距，先在像空间利用一次傅里叶变换重建方法重建物体的像，然后利用参考文献［16］中提出的FIMG4FFT波前重建技术，在一次傅里叶变换方法获得的像平面上截取需要重建的区域，进行了放大率为M=0.07的波前重建，分别得到3种色光的重建像，再由它们合成彩色图像。图4a和图4b中给出了分别使用透镜焦距标称值和测量值进行重建而获得的彩色图像。

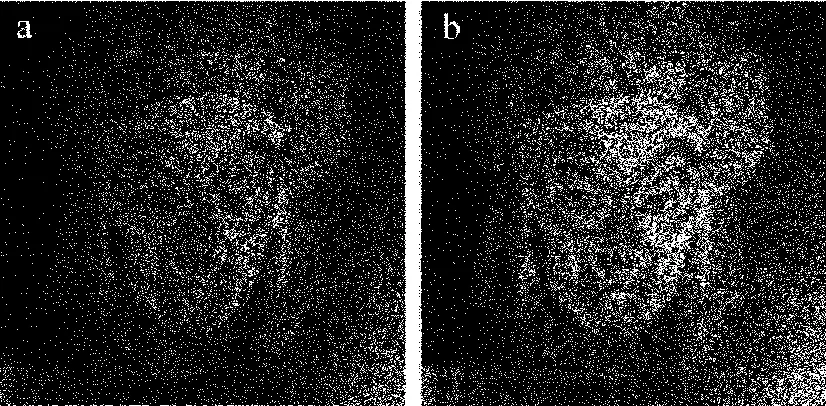
Fig.4 Comparison of color image synthesis before and after the correction of lens focal lengtha—before focus correction b—after focus correction

可以看出，如果不考虑色差，按照透镜焦距标称值f=-100mm进行彩色数字全息波前重建图像质量与用焦距测量值的重建图像质量相当。

3 结论

基于数字全息的透镜焦距测量方法，透镜的测量值与标称值相差1%左右。在数字全息检测研究中，由于获得高质量的重建图像是实现准确检测的前提，实验中所获得的3种色光下的透镜焦距值符合随波长增大而增大的规律，与理论计算相吻合。而且这一方法可以推广到任意透镜组合，检测透镜组合的等效焦距，其有着广泛的应用空间。在本实验中，实验原理易懂、光路搭建简便，利用CCD记录干涉条纹是一种非接触式测量方法，所以精确度高，很适合实验室的操作。期望本文中提出的方法能为彩色数字全息研究提供一个有益的参考。

［1］ HARIHARAN P.Optical holography:principles，techniques，and applications［M］.Cambridge，UK:Cambridge University Press，1996:181-210.

［2］ GOODWAN J W.Introduction to Fourier optics［M］.3rd ed.Beijing:Publishing House of Electronics Industry，2006:326-339(in Chinese).

［3］ YU M W.Optical holography and the application［M］.Beijing:Beijing University of Science and Technology Press，1996:17-29(in Chinese).

［4］ LI J Ch，XIIONG B H.Information optics theory and calculations［M］.Beijing:Science Press，2009:574-591(in Chinese).

［5］ YAMAGUCHI I，KATO J，OHTA S.Surface shape measurement by phase-shifting digta1 holography［J］.Optical Renew，2001，8(2):85-89.

［6］ WANG Y X，WANG D Y，ZHAO J，et al.Profile measurement for micro-optical component by using digital holographic microscopy［J］.Acta Optica Sinica，2011，31(4):109-114(in Chinese).

［7］ LI J Ch，PENG Z J，FU Y Ch.Research of digital holographic object wave field reconstruction in image and object space［J］.Chinese Physics Letters，2011，28(6):064201.

［8］ JIA F，FENG Z Y，ZHOU L B，et al.Three dimensional surface shape measurement of big objects by pre-imaging digital holography［J］.Acta Photonica Sinica，2008，37(11):2239-2243(in Chinese).

［9］ LOU Y L，LI J Ch，ZHANG Y A，et al.Optimization research for digital hologram recording system of big objects［J］.Proceedings of the SPIE，2010，7848:1-9.

［10］ ZHU X M.Using the spectrometer measuring concave lens focal length［J］.Physics Bulletin，2010，10(10):7-9(in Chinese).

［11］ YU T，GU J G，SHAO Z Q，et al.Exploration of measuring concave lens focal length of laser method［J］.University Physics Experiment，2010，23(5):49-51(in Chinese).

［12］ YANG G J.Determination of the focal length of concave lens reflection［J］.University Physics Experiment，2000，13(1):17-21(in Chinese).

［13］ YAO Q J.Optical tutorial［M］.Beijing:Higher Education Press，1990:424(in Chinese).

［14］ CUI H B，LI Y P，DUAN K M.Optics［M］.Beijing:Science Press，2008:224(in Chinese).

［15］ LI J Ch，PENG Z J，TANKAM P，et al.Digital holographic reconstruction of a local object field using an adjustable magnification［J］.Journal of the Optical Society of America，2011，28(6):1291-1296.

［16］ ZHANG J Q，ZHANG Y P，WU Sh，et al.Study on fast accomplishment of multiple-style reconstruction images of CGH［J］.Laser Technology，2013，37(1):40-43(in Chinese).