双曲余弦高斯光束在非Kolmogorov湍流中的湍流距离

汤明玥，李宾中

(川北医学院基础医学院，南充637000)

引 言

在激光理论中，湍流距离是用来定量描述湍流对光束扩展影响的物理量，定义为由于湍流导致光束横截面积扩展达湍流中该处横截面积10%时的距离。近年来，国内外科研工作者们利用湍流距离定量地研究了湍流对激光束扩展的影响［1-5］。2009年，ZHONG等人研究了环状光束在湍流中的扩展，并发现湍流距离随光束遮拦比ε的增大而增大，即ε越大湍流对光束扩展的影响就越小［4］。2011年，LIU等人求解出部分相干双曲余弦高斯列阵光束的湍流距离的半解析表达式，并研究了湍流距离随光束参量、湍流强度及光束叠加方式的变化情况［5］。然而，这些研究都是针对理想大气湍流，如常规Kolmogorov湍流，但近来实验测量结果与理想的Kolmogorov湍流模型有较大的偏差［6］。TOSELLI等人［7］通过引入湍流广义指数和广义振幅因子来描述非Kolmogorov湍流模型，所得理论研究结果与实验数据更为接近。基于该模型，国内外学者于近期对激光束在非Kolmogorov湍流中的传输特性开展了一些相关的研究［8-12］。

另一方面，余弦高斯光束是厄米正弦类高斯光束的一种特例，厄米正弦类高斯光束是傍轴近似下波动方程的新解，它代表了一大类光束［13-14］。余弦高斯光束是在传输过程中不能保持其形状不变的一类光束，选取一定的偏心参量能使其在空间某处得到近平顶分布的光束。1999年，WANG等人指出新型的CO2激光器的谐振腔具有特殊的机构，即在其中一块反射镜上带有相位台阶，从而提出余弦高斯光束［15］。基于余弦高斯光束在优化激光放大器的效率方面有一定实际应用价值，国内外科研工作者对此类光束展开了大量研究。

作者选用部分相干双曲余弦高斯光束作为激光模型，推导出了部分相干双曲余弦高斯光束在非Kolmogorov湍流中的湍流距离解析表达式，并研究了湍流参量和光束参量对湍流距离的影响，得到一些了有意义的结果。

1 理论模型

以部分相干双曲余弦高斯光束为理论模型，其在z=0处的交叉谱密度函数表示为［16］:

式中，w0和σ0分别为z=0处光束的束腰及相干长度，Ω0是与双曲余弦有关的光束参量［14］，x1′，x2′指z=0平面处，x轴坐标中的两点位置。

基于广义惠更斯-菲涅耳原理，光束通过湍流传输的平均光强表示为［17］:

式中，x指z≠0时x轴某点位置，λ为波长，k是波数(k=2π/λ)，ψ(x，x′)表示湍流介质特性决定的复相位函数，* 是共轭，〈〉m是系综平均，且其中，J0为0 阶 Bessel函数，Φ(κ，α)为湍流介质的折射率起伏空间谱密度函数。κ，α，ξ分别表示空间频率、湍流广义指数和传输路径参量。湍流模型采用非Kolmogorov统计，则Φ(κ，α)可表示为［7］:

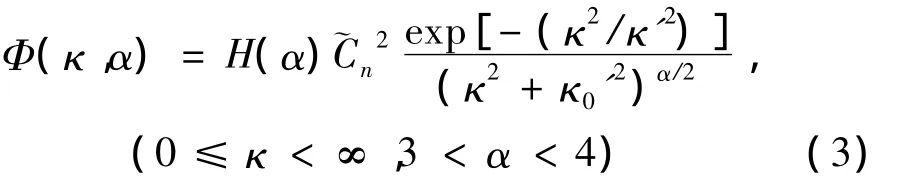
式中，l0和 L0分别为湍流的内尺度及外尺度，κ′=c(α)/l0，κ0=2π/L0，~Cn2为广义折射率结构函数(单位为m3-α)。另外，H(α)和 c(α)的表达式由参考文献［7］中给出。若 α =11/3，H(11/3)=0．033，C~n2=Cn

2，即简化为常规 Kolmogorov 功率谱［7］。

根据二阶矩束宽的定义［1］，并引入新的变量u=(x1′+x2′)/2，v=x1′-x2′。经过复杂的积分运算可得部分相干双曲余弦高斯光束在非Kolmogorov湍流中的二阶矩束宽为:

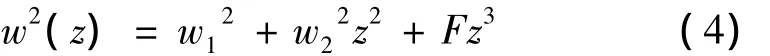
其中:

式中，β=σ0/w0为光束相干参量，δ=Ω0w0为光束离心参量［15］。

若F=0，(4)式化简为部分相干双曲余弦高斯光束在自由空间中的二阶矩束宽:

(4)式的前两项表示部分相干双曲余弦高斯光束通过自由空间传输的二阶矩束宽，它与光束参量(w0，λ，β，δ)相关;第3项为湍流导致的光束扩展，结合(3)式可知，其与湍流广义指数α、内尺度l0及外尺度L0相关。

湍流距离zt指光束扩展开始明显受到湍流影响的传输距离，是定量描述湍流对光束扩展影响的物理量，其定义为湍流导致光束扩展达10%的距离［1］，将(4)式和(8)式代入，得zt满足三次方程，即:

求解上式，zt有唯一实解，即:

其中，

(10)式为部分相干双曲余弦高斯光束传输于非Kolmogorov湍流的湍流距离zt解析式，光束参量(w0，λ，β，δ)与湍流参量(α，L0，l0)对 zt有一定影响。显然，zt表征湍流对光束扩展的影响，即zt越小，光束扩展受湍流的影响则越大。

2 数值计算与分析

Fig.1 ztversus Cn2

图1 中给出了常规Kolmogorov湍流中湍流距离zt随折射率结构常数Cn2的变化，其中计算参量λ=1.06μm，α =11/3，w0=0.05m，β =0．1，δ=2，L0=20m，l0=0.01m。

图2和图3为湍流距离zt对不同内尺度l0、外尺度L0随湍流广义指数α的变化情况，计算参量~Cn2=2×10-15m3-α，其余计算参量与图1一致。

Fig.2 ztversus α for different values of l0

Fig.3 ztversus α for different values of L0

由图2可知，zt随着Cn2的增大而减小，即湍流的增强使得湍流距离缩短，这也可从(10)式得到该结论。图2显示zt随α的增大而先减小后增大，且在α=3．11处时存在极小值，其物理原因:在(7)式中湍流项F是一个有关α的函数，F随α增大而先增大后减小，且在α=3．11处时取最大值，极大的湍流值将导致极小的湍流距离。另外，图2还说明，zt随l0的增大而增大，当α＞3．11时，随着α的增大，各条曲线之间的差别在逐渐缩小，即广义指数α越大，内尺度l0对于湍流距离的影响越小。

图3显示，当0＜α＜3．6时，各条曲线之间无差别;而当3．6＜α＜4时，zt随L0的增大而减小。

Fig.4 ztversus α for different values of β

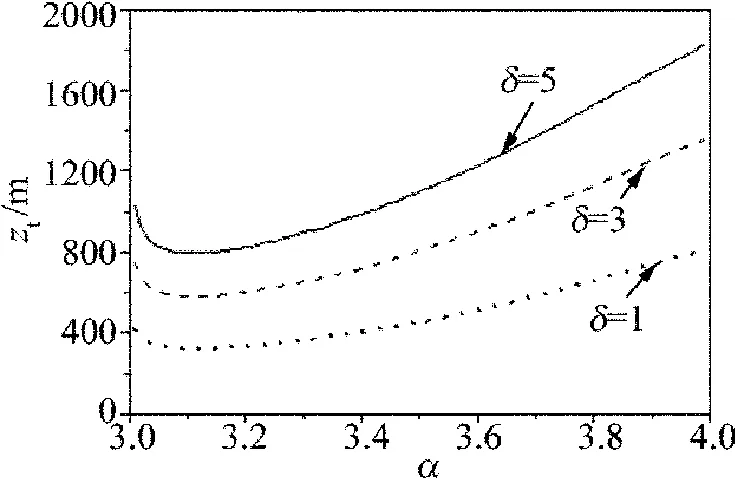
Fig.5 ztversus α for different values of δ

图4 、图5为湍流距离zt对不同光束参量(光束相干参量β、光束离心参量δ)随湍流广义指数α的变化情况。

由图4可以看出，zt随β的增加而逐渐减小，即相干性越差的光束湍流距离越大，光束受湍流的影响则越小;而当β取值较大(β=1)时，湍流距离zt随α的变化则不明显。

图5指出，zt随光束δ的增大而增大，即离心参量越大，湍流距离越大，光束扩展受湍流的影响越小。这与常规Kolmogorov湍流中的研究结果是一致的。

3 结论

基于广义惠更斯-菲涅耳原理，并采用非Kolmogorov湍流模型，推导出了部分相干双曲余弦高斯光束在非Kolmogorov湍流中的湍流距离，研究了湍流参量与光束参量对湍流距离的影响。研究发现:在常规Kolmogorov湍流中，湍流距离zt随着折射率结构常数Cn

2的增大而减小，即湍流的增强使得湍流距离缩短;在非Kolmogorov湍流中，湍流距离zt随湍流广义指数α的变化表现出非单调性，zt随α的增大而先减小后增大，且当α=3．11时存在极小值，即此刻湍流对光束扩展的影响最大。湍流距离zt随内尺度l0的增大而增大，且当α＞3．11时，α越大，l0对于zt的影响越小;zt随外尺度L0的增大而减小(仅当3．6＜α＜4时)，而在0＜α＜3．6时，L0的变化对湍流距离zt无影响。光束相干参量β越小和光束离心参量δ越大，湍流距离zt则越大，即β越小、δ越大，光束扩展受湍流的影响就越小。

本文中所得理论结果对部分相干双曲余弦高斯光束在湍流中扩展、方向性的控制及相关应用有实际意义。

［1］ GBUR G，WOLF E.Spreading of partially coherent beams in random media［J］.Journal of the Optical Society of America，2002，A19(8):1592-1598.

［2］ ZHU Zh W，SU Zh P.Spectral change of J0-correlated partially coherent flat-topped beam in turbulent atmosphere［J］.Laser Technology，2012，36(4):532-535(in Chinese).

［3］ JI X L，ZHANG E T，LÜ B D.Spreading of partially coherent flattened Gaussian beams propagating through turbulent media［J］.Journal of Modern Optics，2006，53(12):1753-1763.

［4］ ZHONG Y L，CUI Zh F，SHI J P，et al.Propagation properties of partially coherent flat-topped beam array in a turbulent atmosphere［J］.Laser Technology，2010，34(4):542-546(in Chinese).

［5］ LIU F，JI X L.Turbulence distance of partially coherent cos-Gaussian array beams［J］.Chinese Journal of Lasers，2011，38(7):0713001(in Chinese).

［6］ RAO C H，JIANG W H，LING N.Spatial and temporal characterization of phase fluctuations in non-Kolmogorov turbulence［J］.Journal of Modern Optics，2000，47(6):1111-1126.

［7］ TOSELLI I，ANDREWS L C，PHILLIPS R L，et al.Free space optical system performance for laser beam propagation through non Kolmogorov turbulence for uplink and downlink paths［J］.Proceedings of the SPIE，2007，6708:670803.

［8］ WU G H，GUO H，YU S，et al.Spreading and direction of Gaussian-

Schell model beam through a non-Kolmogorov turbulence ［J］.Optics Letters，2010，35(5):715-717.

［9］ XU H F，CUI Z F，QU J.Propagation of elegant Laguerre-Gaussian beam in non-Kolmogorov turbulence［J］.Optics Express，2011，19(22):21163-21173.

［10］ HE X M，LÜ B D.Propagation properties of partially coherent Hermite-Gaussian beams through non-Kolmogorov turbulence［J］.Chinese Physics，2011，B20(9):094210.

［11］ DENG J P，JI X L，LU L.Propagation of polychromatic partially coherent decentred laser beams propagating in non-Kolmogorov turbulence［J］.Acta Physica Sinica，2013，62(14):144211(in Chinese).

［12］ HUANG Y P，ZENG A P.Propagation properties of Hermite-Gaussian beams in non-Kolmogorov turbulence［J］.Acta Photonica Sinica，2012，41(7):818-823(in Chinese).

［13］ LIU L，HAO Zh Q.Propagation of sinh-Gaussian beams in gradientindex medium［J］.Laser Technology，2013，37(1):126-129(in Chinese).

［14］ LI P，KUANG A H.Propagation characteristics of non-paraxial partially coherent Hermite-cosine-Gaussian beams［J］.Laser Technology，2014，38(1):141-144(in Chinese).

［15］ WANG Sh M，LIN Q，JIANG X Q.Cosine-Gauss beam［J］.Acta Photonica Sinica，1999，28(4):367-390(in Chinese).

［16］ JI X L.Influence of turbulence on the Rayleigh range of partially coherent cosh-Gaussian beams［J］.Acta Physica Sinica，2011，60(6):064207(in Chinese).

［17］ ANDREWS L C，PHILLIPS R L.Lazer beam propagation through random media［M］.Washington DC，USA:SPIE Press，1998:17-29.