涉及公共值和公共值集的亚纯函数的正规族❋
李效敏, 王凯梅, 郎 涛
(中国海洋大学数学科学学院,山东 青岛 266100)
涉及公共值和公共值集的亚纯函数的正规族❋
李效敏, 王凯梅, 郎 涛
(中国海洋大学数学科学学院,山东 青岛 266100)
2007年刘晓俊与庞学诚首先研究了亚纯函数及其导函数分担1个具有3个元素的公共值集的正规族问题。 2011年刘晓毅与常建明推广了刘晓俊与庞学诚的相应结果。 本文将在刘晓毅与常建明的有关结果基础上, 进一步研究亚纯函数及其导函数分担公共值集的正规族问题。 本文结果进一步推广了刘晓俊与庞学诚以及刘晓毅与常建明的有关结果。
亚纯函数 ;公共值;公共值集 ; 正规族
0 引言及主要结果

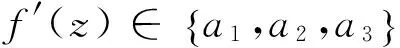
定理1 假设F是定义在区域D内的亚纯函数族,S1⊂C与S2⊂C是2个非空的有限集合。假 设f(z)∈S1并且z∈D,当且仅f′(z)∈S1并且z∈D。 如果下述条件之一成立, 那么F在区域D内正规:
(a) |S1|≥5; (b) |S1|≥3, 并且 |S2|≥3 ;(c) |S2|≥10。
本文将推广上述定理1,证明下述3个定理。
定理2 假设F是定义在区域D内的亚纯函数族,S1⊂C与S2⊂C是2个非空的有限集合。假设f(z)∈S1并且z∈D, 当且仅f(k)(z)∈S1并且z∈D, 其中k≥2, 并且对任意a1∈S1,f-a1的每个零点重数≥k。如果|S1|≥4,那么F在区域D内正规。定理3 假设F是定义在区域D内的亚纯函数族,S1⊂C与S2⊂C是2个非空的有限集合。假设f(z)∈S1并且z∈D, 当且仅f(k)(z)∈S1并且z∈D, 其中k≥2, 并且对任意a1∈S1,f-a1的每个零点重数≥k。如果|S1|=3和|S2|≥3,那么F在区域D内正规。定理4 假设F是定义在区域D内的亚纯函数族,S1⊂C与S2⊂C是2个非空的有限集合。假设f(z)∈S1并且z∈D, 当且仅f(k)(z)∈S1并且z∈D,k≥2, 并且对任意a1∈S1,f-a1的每个零点重数≥k。如果|S2|≥10, 那么F在区域D内正规。
1 几个引理
本节将给出证明本文主要结果所需要的一些引理。假设f是复平面内的1个非常数的亚纯函数。 并假定读者熟悉Nevanlinna理论的基本概念和记号[3-4],例如


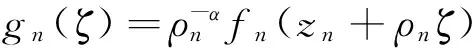
下述引理是著名的Nevanlinna第二基本定理[3-4]:
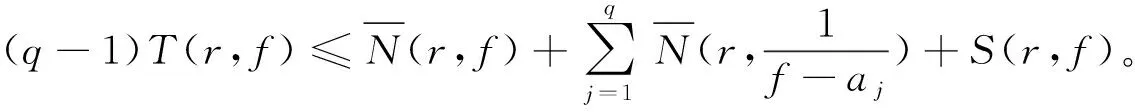
引理3 假设F是区域D内的1个亚纯函数族,k≥2是1个正整数, 再设S⊂C是1个有限复数集,且满足|S|≥4。若对任意f∈F,当f∈S时有|f(k)(z)|≤M, 其中M是1个正常数,并且对任意a∈S,f(z)=a在D上的每个解(如果存在)的重数≥k,那么F在区域D内正规。


注意到ζ0作为g(ζ0)=0的解的重数≥k≥2, 于是ζ0作为g(ζ0)=0的解的重数≥k+1≥3。假设a1,a2,a3,a4是S中4个判别的元素, 则由引理2可得:
即T(r,g)=S(r,g), 这与g为非常数的亚纯函数矛盾。引理3获证。
引理4 假设R是1个 非常数的有理函数,S是1个有穷复数集合。如果R(z)=0当且仅当R(k)(z)∈S, 这里k≥1是1 个正整数,那么R是1个次数≥k的多项式, 并且|S|≤k+1。
证明 由该引理条件可知,S是1个 有限集。

(1)
为一个多项式。注意到
(2)
其中c1,c2,…cq是复常数,于是(1)改写为
(3)
再由(3)和条件R(z)=0当且仅当R(k)(z)∈S可知,R也是多形式, 且不恒为常数, 于是
R(z)=czp(1+o(1)),z→∞
(4)
其中:c≠0是常数;p是某个正整数。由于R(k)(z)不恒为常数,所以p≥k+1,于是由(1)可知A不恒等于零,而且A不恒等于常数。 事实上,若A=b1,其中b1为非零常数,则由(1)可得
RR(k+1)=b1(R(k)-a1)(R(k)-a2)…(R(k)-aq)
(5)
由(4), 比较(5)两边的次数可得
p+(p-k-1)=q(p-k),
即:
(q-2)p=qk-k-1
(6)
再由(6),p≥k+1和假设q≥k+2 可得矛盾,所以A是非常数的多项式。再由(3),(4)以及对数导数引理,经计算可知, 当z→∞有
(7)
其中b2≠0为常数。 由(1),(4)和(7)可得
A(z)=cb2zp-1(1+o(1)),z→∞
(8)
另一方面,注意到R(z)=czp(1+o(1)),由(4)可知, 当z→∞时, 有
R(k)(z)=cp(p-1)…(p-k+1)zp-k(1+o(1))
(9)
和
R(k+1)(z)=cp(p-1)…(p-k+1)
(p-k)zp-k-1(1+o(1))
(10)
将(4),(9)和(10)代入(1)得
A(z)=b3zq(k-p)+2p-k-1(1+o(1)),z→∞
(11)
其中b3≠0是某个常数。最后比较(8)和(11)可得p-1=q(k-p)+2p-k-1,由此得p=k,这与前面得到的结论p≥k+1矛盾。引理4获证。
下述引理是由Hayman-Miles[6]得出的重要结果, 对本文主要结果的证明起重要作用:
引理5[6]假设f是1个复平面上的超越亚纯函数,K>1是1个给定的正常数, 则存在1个仅与K有关的子集M(K)⊂(0,+∞), 其上对数密度不超过δ(K)=min{(2eK-1-1)-1,(1+e(K-1))exp(e(1-K))},使得对每一个正整数k, 有:
2 定理的证明
定理2的证明 假设 |S1|≥4。


gn(ζ)=fn(zn+ρnζ)-a1→g(ζ)
(12)
相应地
(13)
和
fn(zn+ρnζ)-a3=gn(ζ)+a1-a3→g(ζ)+a1-a3
(14)
证明 0是g,g+a1-a2和g+a1-a3的Picard例外值, 从而由引理2可知,g退化为常数,这与前面得到的g为非常数的亚纯函数矛盾。首先证明0是g的Picard例外值。事实上,假设存在一点ζ0∈C,使得
这里
(15)
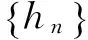
hn(ζ)→h(ζ)
(16)
或者
hn(ζ)→∞
(17)
其中h(ζ)是复平面C上的非常数的亚纯函数,并且不恒等于∞。注意到g不恒为常数,由Huiwitz定理知,存在点列ζn使得gn(ζn)=0并且ζn→ζ0, 于是
(18)
由(18)可知,(16)成立,但(17)不成立。


下面证明下述2个断言: (i)G在复平面C上的零点个数是有限的;(ii)G(ζ)=0当且仅当G(k)(ζ)∈S2。
断言(i)的证明 假设ζ0是g的m0≥1重零点,那么G在 复平面C上的零点个数不超过m0。事实上,假设G在复平面C上有m0+1个判别的零点ξ1,ξ2,…,ξm0,ξm0+1,那么由Huiwitz定理知,存在点列ξnj→ξj(1≤j≤m0+1)使得对充分大的正正整数n,有Gn(ξnj)=0,结合(19)可知gn(ζn+ηnξnj)=0。注意ζn+ηnξnj→ζ0,1≤j≤m0+1,再由(19)和Huiwitz定理可知,ζ0作为g的零点的重数≥m0+1, 这与前面假设矛盾。断言(i)获证。
断言(ii)的证明 假设G(ξ0)=0,ξ0∈C。注意到G不恒为常数,由Huiwitz定理可知,存在点列ζn的某个子序列, 不妨设它本身, 使得ζn→ξ0并且Gn(ξn)=0,即
gn(ζ)=fn(zn+ρn(ζn+ηnξn))-a1=0,
由定理3的条件可知

(20)
再证
(21)
事实上,假设G(k)(ξ0)=b1∈S2,ξ0∈C。首先G(k)不恒等于b1, 否则G(k)=b1, 当b1=0时,G是次数≤k-1的多项式, 这与G是非常数的亚纯函数,并且G的每个零点重数≥k矛盾;当b1=0时,G是次数等于k的多项式, 即
(22)
其中τ0是某个有穷复数。
由(22)可得
(23)
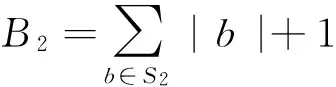
由此结合定理3的条件可得
fn(zn+ρn(ζn+ηnξn))=s1∈S1,
其中s1是S1中的某个元素。若s1≠a1, 则由前面得到的结论:按球距
gn(ζ)=fn(zn+ρnζ)-a1→g(ζ),
可知
(24)
另一方面
a1∈S1
(25)
由(24)和(25)可得矛盾。
若s1=a1, 类似于(24)可得G(ξ0)=0,于是(21)得证。
最后由(20) 和(21)可得断言(ii)。由上面的断言(i)和(ii)完成定理3的证明, 为此分以下2种情形讨论:

T(r,G(k))+S(r,G(k)),
即
(|S2|-2)T(r,G(k))≤S(r,G(k))
(26)
由(26)和条件|S2|≥3可得T(r,G(k))=S(r,G(k)), 这与G(k)为非常数的亚纯函数矛盾。
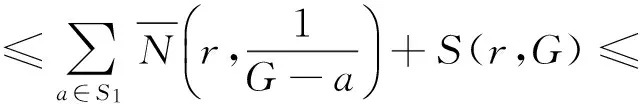
T(r.G)+S(r,G),
由此得T(r,G)=S(r,G), 于是G退化为常数, 这是不可能的。
综上所述,0是g的Picard例外值。同理可证:
0也是g+a1-a2和g+a1-a3的Picard例外值。于是由引理2可知g退化为常数,这是不可能的。
定理3证毕。
定理4的证明 若|S1|≥3, 由定理2和定理3可知,定理4的结论成立。以下假设1≤|S1|≤2,取a1∈S1。 并假设F在D内不正规,从而在某点z0∈D不正规。 不妨设z0=0,F在|z|<1内不正规。 类似于定理3 的证明,由引理1可得 (12)和(15)。于是任意ζ∈C,有
(27)
以及
(28)
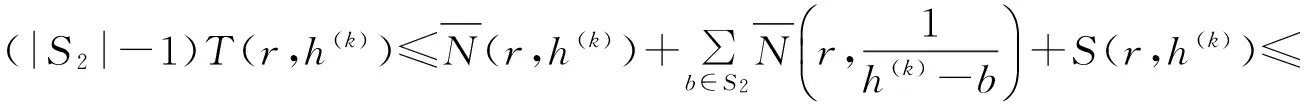
(29)
其中ε为任意给定的正数。由(29)可得3|S2|≤4+(9e+9eε),这与|S2|≥10的假设矛盾。定理4证毕。
[1] 刘晓俊, 庞学诚. 分担值与正规族 [J]. 数学学报, 2007, 50(2): 409-412.
[2] 刘晓毅, 常建明. 分担集合的亚纯函数正规族 [J]. 数学学报 2011, 54(6): 1049-1056.
[3] Yang L. Value Distribution Theory [M]. Berlin: Springer-Verlag, 1993.
[4] Hayman W K. Meromorphic functions [M]. Oxford:The Claredon, 1964.
[5] Schwick W. Sharing values and normality [J]. Arch Math J, 1992, 59: 50-54
[6] Hayman W K, Miles J. On the growth of a meromorphic function and its derivatives [J]. Complex Variables, 1989, 12: 245-260.
[7] Pang X C, Zalcman L. Normal families and shared values [J]. Bull London Math Soc, 2000, 32: 325-331.
AMS Subject Classifications: 30D35; 30D30
责任编辑 陈呈超
Normal Families of Meromorphic Functions Concerning Shared Values and Shared Sets
LI Xiao-Min, WANG Kai-Mei, LANG Tao
(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China )
Liu Xiaojun and Pang Xuecheng firstly study the question of normal families of meromorphic functions sharing a set consisting of three finite values with their derivatives in 2007. In 2011, Liu Xiaoyi and Chang Jianming extended the corresponding results by Liu Xiaojun and Pang Xuecheng. Based upon the corresponding results by Liu Xiaoyi and Chang Jianming, we deeply studied the question of normal families of meromorphic functions sharing sets with their derivatives in the present paper. Moreover, the results in this paper extend the corresponding results given by Liu Xiaojun and Pang Xuecheng and by Liu Xiaoyi and Chang Jianming.
meromorphic functions; shared values ; shared sets; normal families
国家自然科学基金项目 (11171184; 40776006);山东省自然科学基金项目 (Z2008A01; ZR2009AM008;ZR2014AM011)资助
2013-07-16;
2014-05-20
李效敏(1967-), 男, 副教授。 E-mail : xmli01267@gmail.com
O174.52
A
1672-5174(2015)02-138-05
10.16441/j.cnki.hdxb.20130220

