CMIP5气候模式对北半球夏季阻塞的评估❋

吴 静， 刁一娜， 庄绪宗

(1. 中国海洋大学物理海洋实验室，山东 青岛 266100；2. 海军东海舰队海洋水文气象中心，浙江 宁波 315100)



CMIP5气候模式对北半球夏季阻塞的评估❋

吴 静1,2， 刁一娜1❋❋， 庄绪宗2

(1. 中国海洋大学物理海洋实验室，山东 青岛 266100；2. 海军东海舰队海洋水文气象中心，浙江 宁波 315100)

利用美国国家环境预报中心和美国大气科学研究中心(NCEP/NCAR)的逐日再分析资料，评估了耦合模式比较计划第五阶段(The fifth Phase of the Coupled Model Intercomparison Project，简称CMIP5)17个气候模式对于20世纪北半球夏季气候态阻塞频数和振幅的模拟能力，从线性趋势和年际变化2方面评估了欧亚3个关键区(欧洲区、乌拉尔山区和鄂霍次克海区)夏季阻塞频数的模拟能力。结果表明：(1)尽管模式对北半球夏季阻塞频数和振幅的模拟结果存在偏差，但大部分模式可以很好模拟出气候态特征，模式对频数的模拟结果略优于振幅；无论频数或者振幅，CanESM2均为17个气候模式中模拟效果最好的，CMCC-CESM和MIROC-ESM为模拟效果最差的，多模式集成的结果优于大部分单一模式。(2)大多数模式可以较好的模拟出欧亚3个关键区夏季平均阻塞频数和标准差，但对阻塞频数线性趋势和年际变化特征的模拟能力有限。

CMIP5； 夏季阻塞； 模式评估

阻塞系统因其对于中高纬度天气尺度系统影响的重要性，自二十世纪初就受到学者的关注[1]。阻高的建立与崩溃常常决定着短期和中期天气预报的准确性。近年来，越来越多的学者开始关注夏季阻高系统与极端天气现象之间的联系。例如：陶诗言等[2]认为1954和1998年夏季中国长江中下游出现暴雨是亚洲双阻型所提供的大尺度环流条件结果；另外，2010年夏季阻高长期占据欧洲中部地区，导致欧洲中部和东部多地区气温都超出了历史记录[3]，这说明对阻塞系统的研究不但是大气科学理论上需要解决的问题，更是关乎到国计民生的重大课题。在理论研究方面，学者们从能量及波动等动力学角度对阻塞生命循环加以解释。Berggren等[4]最早提出了斜压不稳定天气尺度的扰动会有助于阻塞系统的建立。随后Austin[5]利用非线性共振过程解释了在整个纬圈上激发出的波数为四的阻塞波。罗德海等[6]建立了阻塞与天气尺度波相互作用的模型，提出了瞬变涡动强迫的包络罗斯贝孤立子理论。为了进一步研究阻塞的时空特征，不同的阻塞指数也从不同角度得到定义。Charney[7]，Dole和Gordon[8]，Lejenäs和Økland[9]利用逐日资料定义了持续性异常的阻塞指数。Tibaldi和Molteni[10]为了反应出大气环流中西风的异常状态，在Lejenäs和Økland阻塞指数的基础上添加了约束条件。Pelly等[11]利用PV面上经向位温θ的异常来建立新的阻塞指数。Diao[12]提出的负指数通过跟踪负指数场在特定区域内由正到负再到正的演变过程描述阻塞系统的演变过程。以上这些成果虽有重要的研究意义，但目前天气预报和气候预测对于阻塞系统的考虑仍然是以数值模式手段为主。近些年随着数值模式的不断完善，模式对于阻塞的模拟能力不断提高。Pelly和Hoskins[13]指出，欧洲中心(ECMWF)集成预报系统可以在一周时间尺度之前成功的预报阻塞的出现及消亡。TIGGE中期数值预报模式也被证实具有预报阻塞系统的能力[14]。但需要指出的是，数值模式的模拟结果并非完美。D’Andrea等[15]指出，AMIP模式在中纬度的阻塞的模拟存在偏差，而这一偏差至今在CMIP3耦合模式中仍无法避免[15]。

耦合模式比较计划第五阶段(The fifth phase of the Coupled Model Intercomparison Project，以下简称CMIP5)是世界气象组织气候研究计划(The World Climate Research Program,简称WCRP)的全球耦合模式工作组(Working Group on Coupled Modelling,简称WGCM)利用全球气候模式为IPCC第五次评估报告(the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 简称IPCC AR5)提供的数值模拟实验[17]。其目的是评估各模式对历史气候的反演能力，并从近期和长期2个时间尺度预测未来气候变化并了解一些因素对预测结果的差异，尤其是云和碳循环对模拟结果的反馈。CMIP5中共包括了60个模式实验，由于各个模式间参数化过程、初始场、分辨率以及气候强迫存在差异，因此气候态及气候变率包括气候趋势必然存在差异[18]。对于阻塞系统的评估，Mastato等[19]使用了Pelly等[11]建立在PV面上的阻塞指数，从20世纪和21世纪(碳循环RCP8.5情景试验)2个时间阶段评估了12个CMIP5多模式对冬夏2个季节阻塞频数的模拟能力，结果为：对于夏季阻塞频数，模式在大洋上模拟出的结果多于观测场，在欧亚地区则低于观测场。

本文利用Diao等[12]于2006年提出的负指数，目的是将CMIP5中的17个历史(Historical)气候模式与美国国家环境预报中心和美国大气科学研究中心(NCEP/NCAR)再分析数据结果作对比，评估各模式对1951—2005年北半球夏季气候平均态阻塞的频数与振幅模拟能力。不同于以往学者们研究阻塞系统时将北半球分为太平洋与大西洋-欧洲2个区域的形式[20-21]，本文所关注的是对东亚地区影响较大的欧亚大陆的3个关键区(欧洲区、乌拉尔山区和鄂霍次克海区)。并试图从线性趋势和年际变化两方面评估模式对关键区夏季阻塞频数的模拟能力。

1 资料和方法

1.1 资料

本文采用的是17个耦合模式比较计划(CMIP5)历史(Historical)气候模式试验的1951年1月1日～2005年12月31日逐日高度场资料，北半球夏季选择的是6、7、8三个月。模式资料的基本信息如表1所示。再分析资料采用的是美国国家环境预报中心和美国大气科学研究中心(NCAR/NCEP)提供的水平分辨率为2.5(°)×2.5(°)，时间范围同样为1951年1月1日～2005年12月31日的逐日再分析高度场的再分析数据，以便对模式结果进行评估。

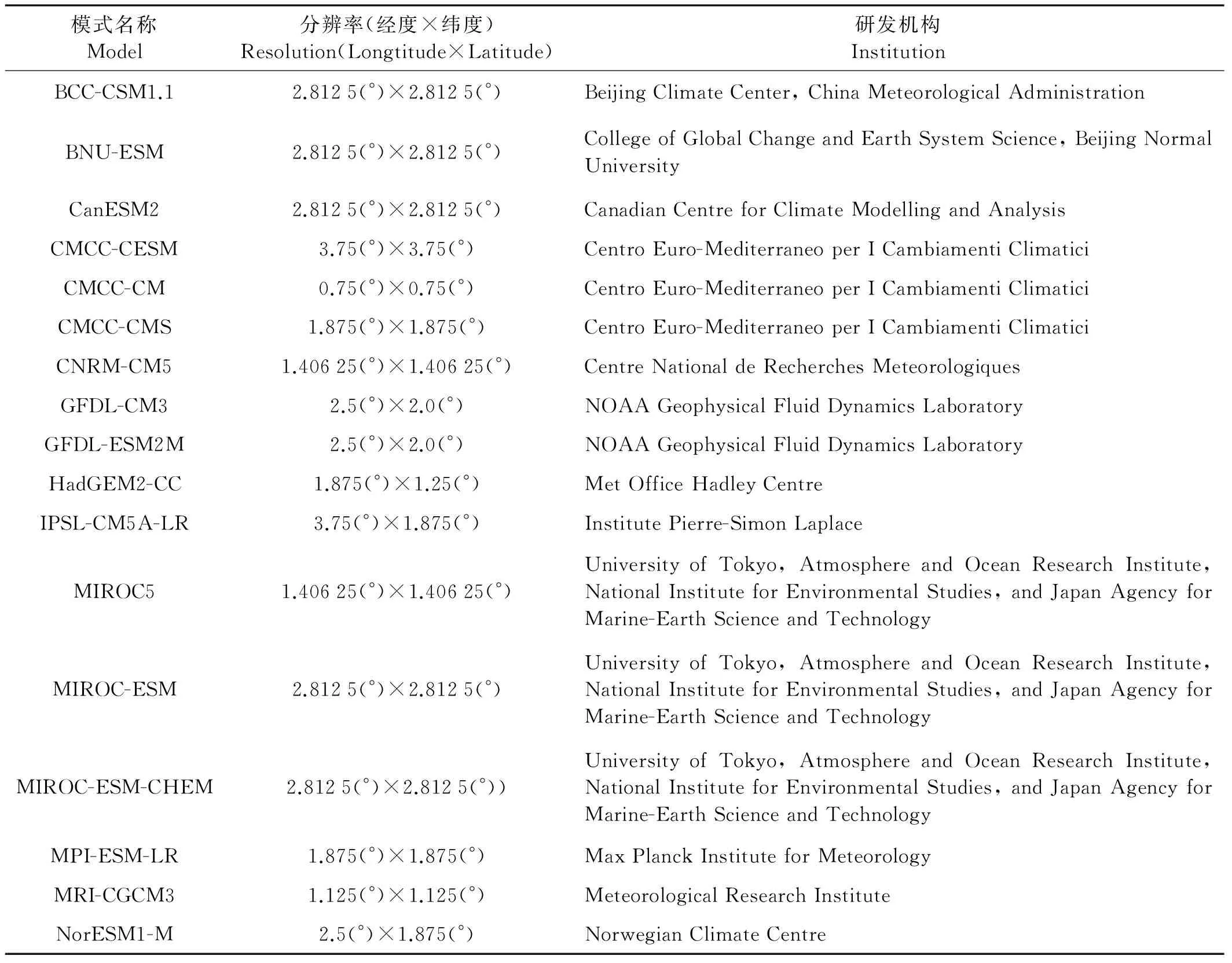
表1 本文采用的17个气候模式的基本信息Table 1 The information of 17 climate models used in current study

1.2 方法

1.2.1 双线性插值 空间差值是将一种分辨率格点上的数值重新分配到另一种分辨率格点上的过程。为了保证模式数据的准确性，本文采用的方法为：在计算单个模式结果的过程中先不进行差值，只在最后模式间比较以及考察模式集成结果的时候才采用双线性差值，即将所有的模式和集成结果统一到2.5(°)×2.5(°)的水平分辨率格点上，这样做的目的是最大程度的减小累计误差。

1.2.2 空间相关系数 相关系数是用来反映变量之间相关关系密切程度的统计指标[22]。本文通过计算每个模式与观测场夏季阻塞的气候态特征的相关系数，对模式的模拟能力进行评估。具体过程采用的是皮尔逊积差相关系数，其定义为2个变量协方差除以2个变量的标准差。2个空间场越相似，相关系数越趋近于1。

1.2.3 阻塞指数 本文采用的阻塞指数是Diao等[12]定义的负指数。负指数的优点在于其增加了指数的自由度，能够反映等压面上的二维信息，它既不同于Dole和Gordon[8]的基于点的指数，也不同于通过抽取几个纬度的信息来反映阻塞的特征；它可以通过跟踪区域来直接反映阻塞的空间和时间上的真实过程，而不是通过间接的途径去反映。这一阻塞指数定义如下：

NI=h(λ,φs)-h(λ,φ),
90°N≥φ≥φs，360°≥λ≥0° 。

其中:h(λ,φ)是500hPa位势高度;φs是发生经向环流等压面下降最大时30°N～40°N之间的某个特定纬度，同时也代表经向环流向南伸出的切断低压或低压槽的位置。负指数是这个特定纬度的等压面高度和所有这个纬度以北的等压面高度的差值。夏季由于受到副热带高压系统的影响，φs取为40°N。

在根据负指数挑选阻塞事件的时，认为当T时刻出现负指数且绝对值不低于50gpm时，作为当此阻塞事件的开始。在连续性方面，认为如果在该格点T+1时刻也出现负指数绝对值不低于50gpm或者在T+1时刻距离上一个时刻发生阻塞事件地点的相对距离少于10个经度，则可认为是一个连续的阻塞过程。当这样的持续事件在某个T+N时刻的阻塞指数小于50gpm，则认为该次阻塞事件结束。其中规定N不小于5d为发生整个阻塞过程的累计持续天数或称为持续时间。整个阻塞过程中出现的最大负指数绝对值为该次事件的振幅。由于阻塞的生命过程伴随着负指数振幅的演变，而两者的演变过程是一致的，因此可用负指数的振幅可以作为阻塞强度的指标。

2 CMIP5模式对夏季北半球阻塞的评估

对于阻塞系统，频数与振幅的分布分别可以反映出活动中心和强度显著区域。为了评估模式对北半球夏季阻塞系统的模拟能力，这里将17个模式夏季气候平均态阻塞频数和振幅空间分布与观测结果做比较，了解模式对北半球夏季阻塞的总体模拟能力和与再分析结果存在的偏差，同时考察多模式集合的模拟效果。

2.1 阻塞频数的模拟能力评估

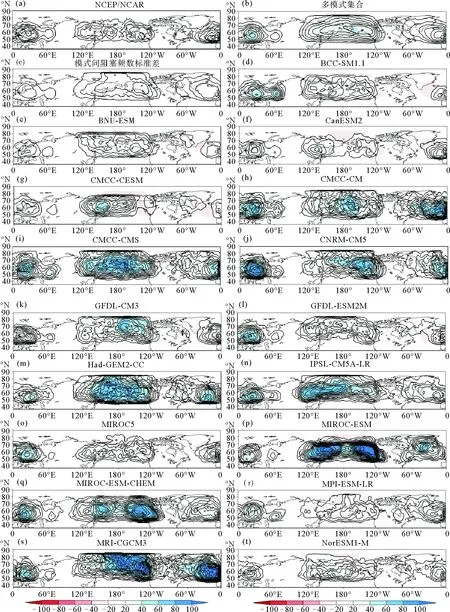
根据负指数的定义，通过17个模式逐日的500hPa高度场可以求出逐年夏季阻塞发生的频数。统计北半球40°N以北每一个格点上夏季阻塞发生的次数，对55年结果累计求出气候态平均场，将得到的数据与NCEP/NCAR资料相减，即得到图1(d-t)各模式的夏季平均阻塞频数的等值线分布与各模式与观测场之间误差的阴影分布。图1(a)(b)(c)分别为NCEP/NCAR和多模式平均的阻塞频数分布，以及多模式之间的标准差分布。由图1(a)可见，夏季阻塞的活动中心共有5个，分别为大西洋和欧洲大陆的2个区，中心在20°W和30°E；乌拉尔山区中心在65°E，鄂霍茨克海区中心位于140°E以及中心在130°W的东太平洋区。这与Diao[12]等的结果吻合。由图1(b)可见，17个多模式集合的模拟结果优于大部分单一模式，这与图3(a)空间相关系数的结果一致，说明多模式集合能够很好的模拟出夏季气候态的阻塞频数。模式集成显示：模式在大西洋和太平洋北部模拟的结果高于观测场，而在欧亚地区低于观测场，此结果与Masato等[19]利用建立在PV面上的阻塞指数所模拟出的结果一致。通过图1和图3(a)分析可知，17个模式中只有3个模式与观测场之间的空间相关系数在0.7以下：BNU-ESM未能模拟出乌拉尔山区活动中心，却在60°W模拟出不真实阻塞频发区；CMCC-CESM模拟出的乌拉尔山活动中心向东偏移至90°E；CMCC-CESM和MIROC-ESM模拟出的活动中心在北大西洋中部而非东北部。

NCEP/NCAR再分析场所表现的5个活动中心里，欧洲大陆区与鄂霍茨克海区为阻塞高频区域，平均每年夏季阻塞频数都在12次以上，其它3个区域频数则相对较少。通过图1中17个模式的阴影分布对比可知，CanESM2、CMCC-CMS、GFDL-ESM2M和MIROC5等4个模式能够较好的模拟出这一特征，并且与NCEP/NCAR结果相比每个格点的误差均在6次之内，CanESM2的模拟结果最优，与再分析数据结果的相似系数达到0.9257，CMCC-CM次之，空间相似系数为0.9130。BCC-CSM1.1、BNU-ESM、CMCC-CM、GFDL-CM3、MPI-ESM-LR、MRI-CGFM3和NorESM1-M等7个模式模拟出的平均阻塞频数偏少，而CMCC-CESM、CNRM-CM5、HadGEM2-CC、IPSL-CM5A-LR、MIROC-ESM、MIROC-ESM-CHEM等6个模式模拟出的平均阻塞频数偏多。其中MIROC-ESM误差最大，与NCEP/NCAR相差最多的格点达35次。17个模式中，CMCC-CESM和MIROC-ESM的模拟效果最差，与再分析数据结果的空间相似系数仅为0.5155和0.6057。为了寻找17个气候模式之间北半球夏季平均态阻塞频数的差异分布特征，将经过双线性差值处理后的气候平均态上的每一个格点的阻塞频数进行模式之间的标准差计算，即得图1(c)所示的17个模式之间北半球夏季阻塞频数的标准差分布。与频数本身情况不同，标准差中心只有2个，1个同样是在欧洲大陆30°E附近，另1个则出现在北美洲西海岸(120°W)，说明以上两个地区模式之间频数的差异最大。大西洋东部和乌拉尔山区由于自身夏季阻塞频数就较少，因此模式间模拟的差异较小。而鄂霍茨克海区虽然是夏季阻塞高频区，但模式间标准差值在此处较小，说明各个模式都能比较好的模拟出此地区夏季阻塞频数。

((a:NCEP/NCAR； b:多模式集合；c:多模式间频数标准差；d-t:CMIP5各模式)，等值线代表阻塞频数，阴影部分代表各模式(多模式集合)与再分析数据的差值，等值线与阴影间隔均为2(次)。 (a) NCEP/NCAR during 1951—2005 ; (b) the ensemble mean; (c) the inter-model frequency standard deviation and (d-t):each CMIP5 models. The color shading represents the differences between the models (multi-model-ensemble included) and NCEP/NCAR reanalysis in frequency. Contour and shading intervals are both 2(2,4,6,…).)

图1 1951—2005年北半球夏季平均阻塞频数分布
Fig.1 Spatial distribution of summer mean frequency of blocking

2.2 阻塞振幅的模拟能力评估

与阻塞频数相似，通过累计17个模式1951—2005年夏季北半球40°N以北每一个格点上每一次阻塞过程的振幅，通过累积结果求出气候平均场，再将得到的数据与再分析资料相减，即得到图2(d～t)各模式的夏季平均阻塞振幅的等值线分布与各模式与观测场之间误差的阴影分布。图2(a)(b)(c)分别为NCEP/NCAR和多模式集合的阻塞振幅分布，以及多模式之间的标准差分布。由图2(a)可见，夏季北半球阻塞强度最强的4个区域为欧洲区(30°E)、鄂霍茨克海区(130°E)太平洋东北部(150°W)和大西洋东北部(10°W)。乌拉尔山区虽同样为阻塞频发区域，但强度却偏较。另外，对比图3(a)和(b)可知，17个CMIP5模式对于北半球夏季气候态阻塞振幅的模拟结果稍弱于频数。且由图2(b)可知，与频数的模拟情况相似，对于阻塞振幅，多模式集合的模拟结果同样优于大部分单一模式，与NCEP/NCAR再分析空间相关系数为0.8011(见图3)，通过了95%的显著性检验，能够很好的模拟夏季气候态北半球阻塞系统的振幅分布。与阻塞频数相似，将经过双线性差值处理后的气候平均态上每一个格点的阻塞振幅进行模式之间的标准差计算，得到图2(c)所示的17个模式之间北半球夏季阻塞振幅的标准差分布。由图可见，17个模式之间的模拟结果也存在有较大差异，主要表现在东北太平洋和东北大西洋这2个区域模式之间的标准差最大，说明这2个区域阻塞振幅模拟结果的差异是模式之间的主要区别所在。17个模式中，只有一个模式——CMCC-CESM对于太平洋东北部和大西洋东北地区的模拟结果都明显小于观测值，而它与NCEP/NCAR所对应的空间相关系数只有0.5408，为17个模式中的最低值。而MIROC-ESM在东北太平洋区域的振幅结果高于观测场达到140位势米，整体所模拟出的相关系数也仅为0.5820。相比而言，CanESM2和MIROC5对阻塞振幅的模拟结果最好，与NCEP/NCAR的相关系数达到0.9027和0.8776，且每个格点的振幅与观测值相减后绝对值都不超过60位势米，能够很好的模拟夏季平均阻塞振幅的空间分布的主要特征。

值得注意的是，CanESM2、CMCC-CM、MIROC5和MPI-ESM-LR等4个模式无论频数或者振幅都是17个CMIP5气候模式中模拟效果最好的，此4个模式集成的阻塞频数和振幅的空间分布与NCEP/NCAR再分析资料的空间相似系数分别为0.9407与0.9108。从动力学角度分析可知，阻塞过程对应局地的大气环流由纬向型转为经向的斜压过程，且阻塞事件通常发生在中纬度急流的出口处，因此急流的平均位置与强度对于阻塞模拟至关重要[11]。另外，风暴轴和定常波分别作为天气尺度涡动带和地形等强迫出的准定常行星波，与大气阻塞在空间上和时间场也存在密切联系[23]。图4为对于阻塞振幅和频次平均态模拟效果最好的4个模式——CanESM2、CMCC-CM、MIORC5和MPI-ESM-LR和2个最差的模式CMCC-CESM和MIROC-ESM对于北半球夏季西风急流、风暴轴和定常波平均态的多模式集成。4个最好的模式集成的空间分布与再分析场的空间相似系数分别为0.9527、0.9693和0.9113，两个最差的模式对应的相关系数为0.8566、0.8416和0.6796，说明西风急流、风暴轴和定常波是控制阻塞系统的重要因素，只有提高以上3个因素空间位置和强度的模拟能力，才可将阻塞的活动中心和强度显著区域做到成功模拟。

3 CMIP5模式对北半球夏季欧亚地区阻塞频数线性趋势和年际变化特征的评估

由以上分析可知，对于北半球夏季气候气候态阻塞系统的模拟能力而言，大多数CMIP5气候模式可以较好的模拟出大气阻塞的活动中心与强度显著区域。但从气候预测角度来讲，模式对气候要素的年际变率的模拟更为关键，只有掌握气候要素的年际和年代际变化才可以加强预报的准确性[24]。中国地处东亚，夏季鄂霍茨克海地区的阻高形势的维持是梅雨发生的大气环流背景，乌拉尔山区的异常频繁的阻塞事件是引发1998年长江洪水的重要原因[25]，因此掌握东亚上、下游地区的阻塞特征显得尤为关键。根据再分析资料阻塞特征的统计分布，将欧亚阻塞关键区域分为以下3个：欧洲区(0°～50°E,40°N～70°N)、乌拉尔山区(50°E～90°E,40°N～70°N)和鄂霍次克海区(110°E～160°E,40°N～70°N)。图5所示为1951—2005年17个CMIP5气候模式、多模式平均与再分析数据下3个关键区夏季平均阻塞频数的年际变化特征。17个CMIP5模式与再分析资料下的阻塞频数的年际变化存在不同程度的偏差，说明模式对于欧亚阻塞频数的模拟能力有限。下面将通过进一步考察这55年期间，17个模式对每个关键区平均的阻塞频数进行线性趋势的模拟，以及夏季平均阻塞频数和年际之间的标准差分布，并试图通过功率谱分析找出主周期，模拟17个CMIP5模式自上世纪中叶以来55年阻塞频数的变化特点。

((a):NCEP/NCAR； (b):多模式集合；(c):多模式间频数标准差；(d～t):CMIP5各模式)；等值线代表阻塞振幅，阴影部分代表各模式(多模式集合)与再分析数据的差值，等值线与阴影间隔均为10(gmp)。(a) NCEP/NCAR during 1951—2005 ; (b) The ensemble mean; (c) The inter-model amplitude standard deviation； (d-t)Each CMIP5 models. The color shading represents the differences between the models (multi-model-ensemble included) and NCEP/NCAR reanalysis in amplitude. Contour and shading intervals are both 10(10,20,30,…)gmp.)

图2 北半球夏季阻塞振幅分布
Fig.2 Spatial distribution of summer mean amplitude of blocking

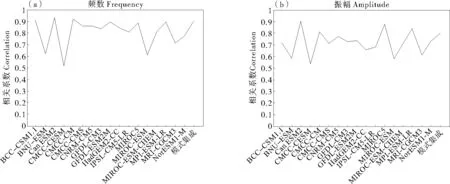
图3 CMIP5模式(包括多模式集合)1951—2005年夏季气候平均态阻塞频数和振幅与NCEP/NCAR的空间相关系数Fig.3 Spatial correlation coefficients between summer mean frequency and amplitude of blocking from CMIP5 models (multi-model-ensemble included) and NCEP/NCAR reanalysis during 1951—2005

((a)、(b)、(c):西风急流, 等值线间隔为5 m/s；(d)、(e)、(f):风暴轴，等值线间隔为10 m2s-2；(g)、(h)、(i):定常波, 等值线间隔为10gmp。(a),(b),(c) Westly jet, contour interval is 5 m/s. (d),(e),(f) Storm tracks, contour interval is 10 m2s-2. (g),(h),(i) Stationary waves, contour interval is 10 gmp.)

图4 NCEP/NCAR对于夏季气候平均态阻塞频数和振幅模拟最好的4个多模式集合和2个最差的模式对北半球1951—2005年夏季平均西风急流、风暴轴以及定常波分布
Fig.4 Distribution of mean state of westly jet,storm tracks and stationary waves from NCEP/NCAR, multi-model-ensemble (MME) of best four and worst two models in stimulating summer frequency and amptitude over North Hemisphere (time series:1951—2005)

3.1 线性趋势分析

对于欧洲区(见图6)，NCEP/NCAR表现出的近55年阻塞频数的线性趋势是下降的，斜率为-0.0461，即平均每年夏季阻塞频数减少0.0461次。与再分析资料相比，9个模式呈线性下降趋势，其中CMCC-CESM和IPSL-CM5A-LR能很好的与NCEP/NCAR结果吻合。8个模式则相反呈现上升趋势，没能模拟出欧洲区夏季阻塞频数随时间的变化趋势。与欧洲区相同，再分析数据对于乌拉尔山区表现出的线性趋势同样是下降的，斜率为-0.0518。17个模式中有9个斜率为负，其中CMCC-CMS模式模拟出了最接近于再分析数据的结果，但两者斜率之差仍然相差较大，为-0.0287。其余模式均不能模拟出乌拉尔山区夏季阻塞的线性趋势。与前两个关键区不同，鄂霍茨克海区夏季阻塞频数是逐年增加的，平均每年增加0.0665次。通过比较可知，MIROC-ESM-CHEM和MIROC-ESM模式最接近于NCEP再分析数据的斜率。但从图8也可见，这两个模式虽然线性趋势与再分析一致，但每年的频数均多于观测值，这一结论与图2(p～q)的模拟结果一致。

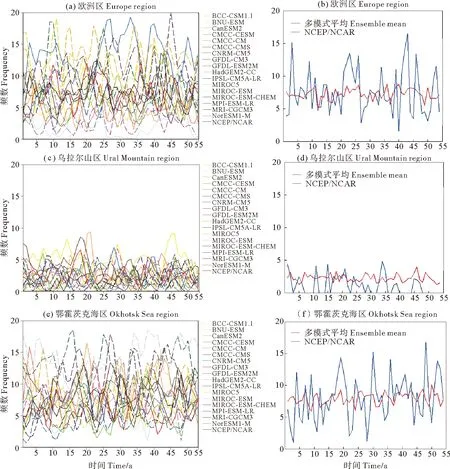
图5 CMIP5模式、多模式集合及NCEP/NCAR对欧亚三个关键区1951—2005年夏季平均阻塞频数年际变化分布Fig.5 Distribution of interannual variability of frequency from CMIP5 models, multi-model-ensemble (MME) and NCEP/NCAR over different regions (time series:1951—2005)

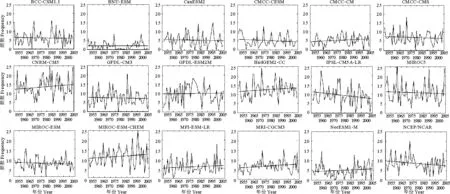
(曲线代表频数；直线代表线性趋势。Curve lines represent frequency; Straight line represent linear tendency.)图6 CMIP5模式与NCEP/NCAR对欧洲区1951—2005年夏季阻塞频数线性趋势模拟分布Fig.6 Distribution of linear tendency of blocking frequency over Euro region in summer ( time series:1951—2005)

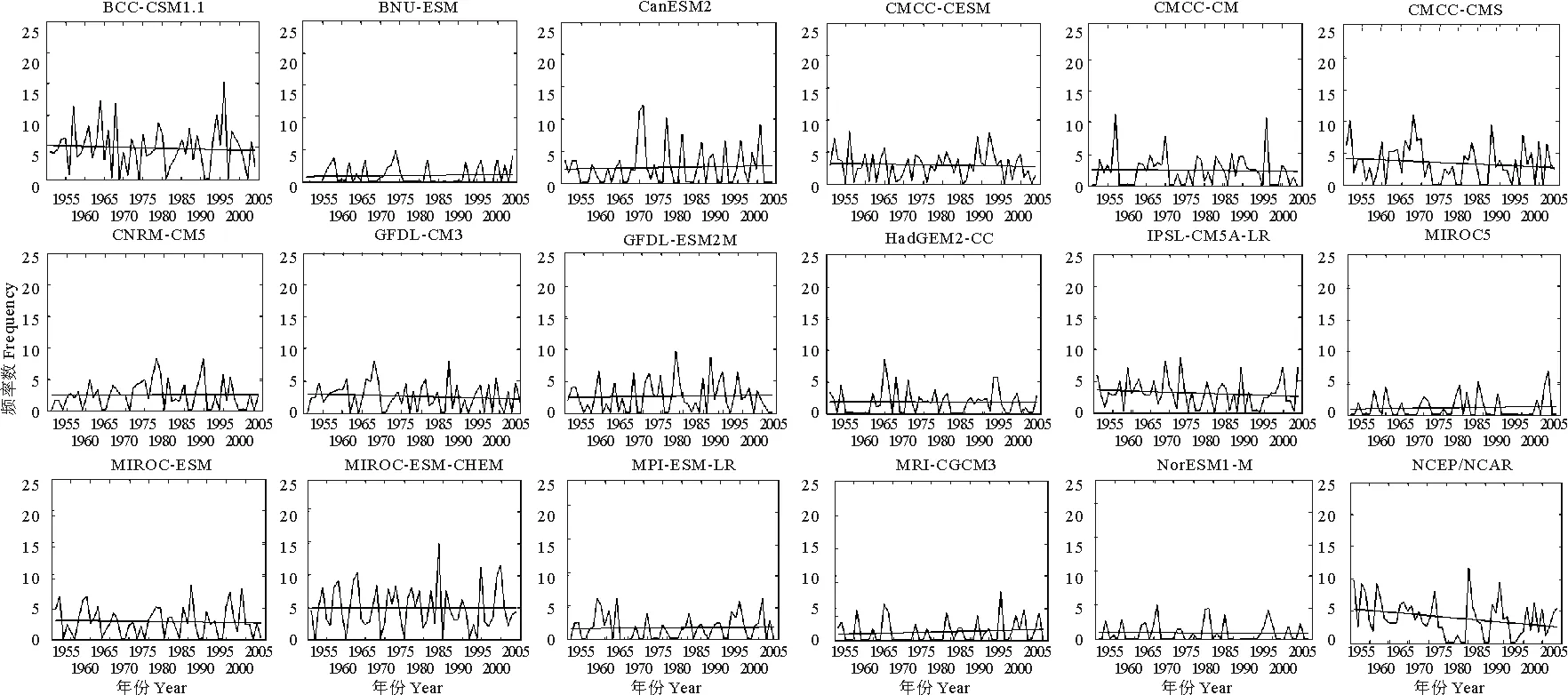
图7 同图6，但为乌拉尔山区Fig.7 Same as Fig. 6, but for Ural Mountain region

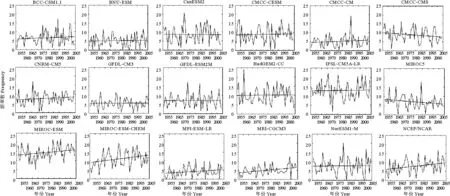
图8 同图6，但为鄂霍茨克海区Fig.8 Same as Fig. 6, but for Okhotsk Sea region

3.2 平均频数与标准差

图9给出了3个阻塞关键区各模式和NCEP/NCAR再分析数据的夏季平均的阻塞频数与55年际之间标准差分布。由图9(a)可以看出，对于欧洲区频数的模拟，17个模式中与再分析数据频数差值的绝对值大于3的只有1个，为CMCC-CMS，它模拟出的欧洲区夏季平均阻塞频数较再分析结果多3.415次。其余模式结果与再分析数据相比绝对值均不超过1.5次。就欧洲区55年阻塞频数的标准差而言，NCEP/NCAR再分析结果为8.5452；17个CMIP5模式中，只有6个模式模拟出的标准差高于再分析数据，说明其他11个模式模拟出的阻塞频数逐年变化都比再分析数据更加稳定。而由图2可知，相比于欧洲区，乌拉尔山区由于本身夏季阻塞发生的次数就比较少，因此在多模式比较中，无论频数还是标准差，17个模式的模拟结果与观测场相比都十分相似。

与前两个区域相比，鄂霍茨克海区夏季阻塞发生的次数明显偏多，6个模式的模拟结果与再分析相减的结果绝对值大于3(次)，其中IPSL-CM5A-LR和MIROC-ESM模拟出的年平均阻塞次数偏多，BNU-ESM、CMCC-CM、MPI-ESM-LR、MRI-CGCM3等4个结果偏小。这与图2的北半球阻塞频数气候平均态分部相一致。除此，由图9(c)仍可知，除MPI-CGCM3，其余16个模式均能很好的模拟鄂霍茨克海区1951—2005年夏季阻塞频数标准差。

3.3 功率谱分析

通过比较功率谱图上各个谐波方差的大小，可对欧亚3个关键区夏季阻塞频数变化的周期进行提取。由图10可见，NCEP/NCAR的欧洲区方差峰值对应的周期为3.37年，但此峰值并没有通过置信度为95%的显著性检验，因此再分析数据的结果为：1951—2005年欧洲区夏季平均阻塞频数并不存在包含在时间函数中的主要周期。反观模式结果，17个模式中有CanES M2、GFDL-ESM2M、IPSL-CM5A-LR、CNRM-CM5等4个模式同样不存在主周期，剩余的13个模式均存在这2～5年的主周期，4个不存在主周期的模式谐波方差图上均可以找到2～5年的峰值。对于乌拉尔山区(见图11)，NCEP/NCAR表现出包含在时间函数中的主要周期有3个：T1=8.31年、T2=7.71年和T3=2.16年。这说明乌拉尔山区夏季阻塞频数存在有显著的8年左右的周期，并且有2年左右的周期振荡。CMIP5各模式中，能模拟出8年左右周期的模式只有2个，为CMCC-CESM和MPI-ESM-LR；能模拟出2年左右的模式有8个，没有任何一个模式同时模拟出这2个主周期，其余模式均无法正确模拟出乌拉尔山区夏季阻塞频数的变化。同样，图12表明鄂霍茨克海区夏季阻塞的存在约5.5年的周期，表现出这一特点的模式有MRI-CGCM3、BCC-CSM1.1、HadGEM2-CC、GFDL-ESM2M和BNU-ESM等5个。

图9 CMIP5模式与NCEP/NCAR对欧亚3个关键区1951—2005年夏季平均阻塞频数与标准差分布Fig.9 Distribution of summer mean blocking frequency and standard deviation from CMIP5 models and NCEP/NCAR over different regions (time series:1951—2005)

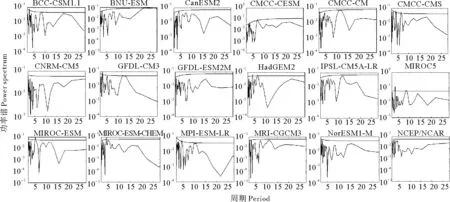
(虚线为功率谱对应各谐波的F检验值。Dashed line donates the corresponding value of F test.)图10 CMIP5模式与NCEP/NCAR对欧洲区1951—2005年夏季阻塞频数的功率谱分析Fig.10 Power spectrum analysis of summer blocking frequency from CMIP5 models and NCEP/NCAR over Euro regions (time series:1951—2005)

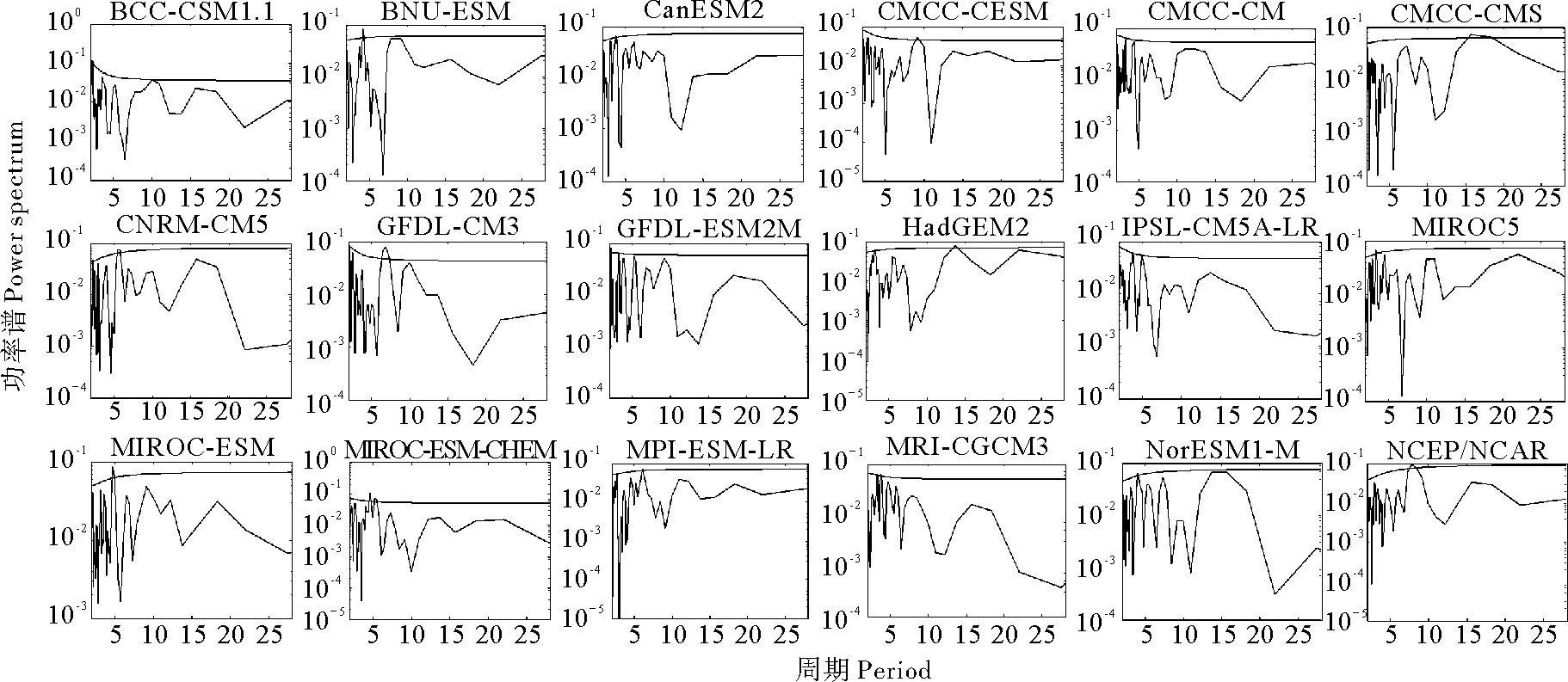
图11 同图10，但为乌拉尔山区Fig.11 Same as Fig. 10, but for Ural Mountain region

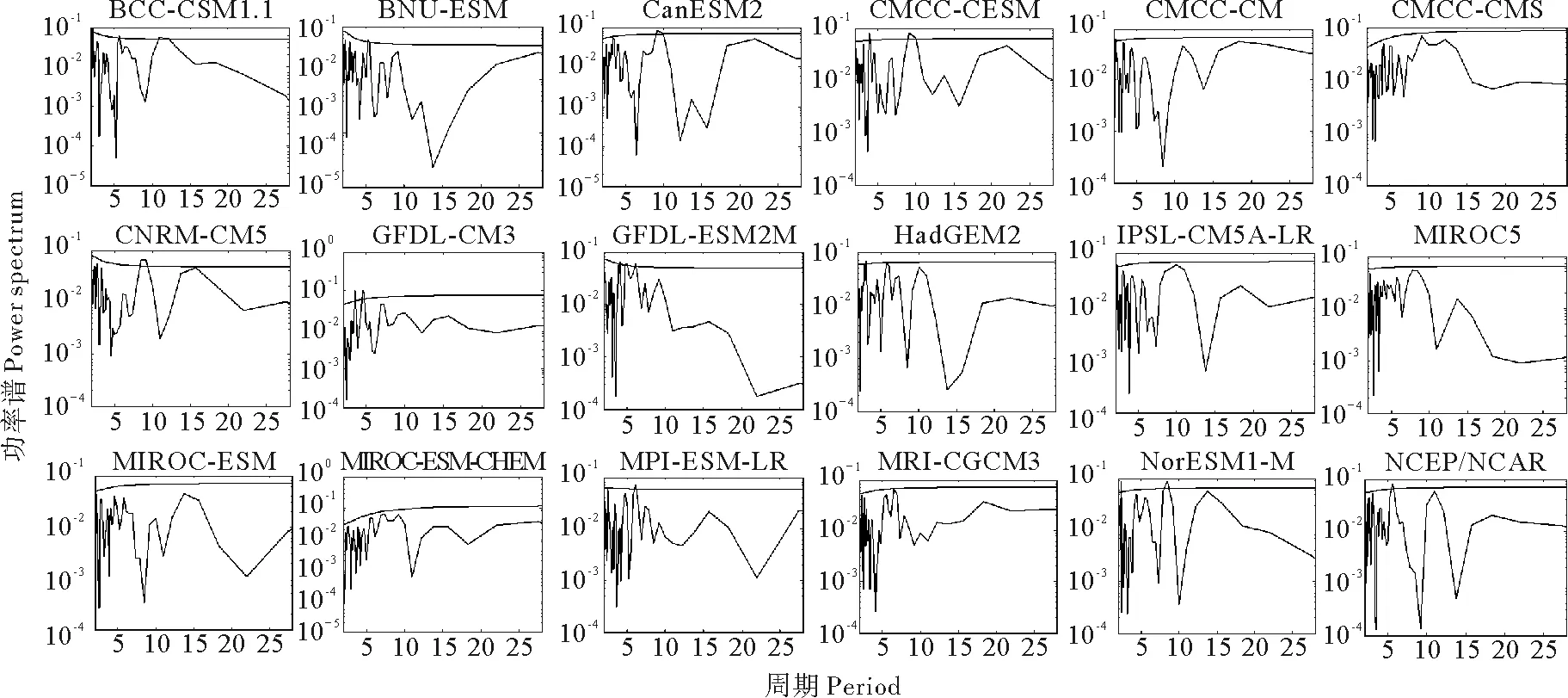
图12 同图10，但为鄂霍茨克海区Fig.12 Same as Fig. 10, but for Okhotsk Sea region

4 结论

本文使用了Diao等[12]于2006年提出的负指数作为阻塞指数，同时利用NCEP/NCAR再分析资料，对17个CMIP5气候模式对北半球夏季阻塞的频数与振幅的模拟能力进行评估。需要指出的是，不同于以往的研究结果，本文不仅模拟了CMIP5多模式对于夏季气候态阻塞频数的模拟能力，同时也对指示阻塞事件显著性的指标——阻塞振幅的模拟能力也进行了考察。通过空间相关系数比较了各个模式和多模式集合对再分析资料的反演能力。通过线性趋势分析与功率谱分析，评估了各模式对影响中国夏季气候的欧亚地区3个关键区域(欧洲区、乌拉尔山区和鄂霍次克海区)的夏季阻塞频数的线性趋势和年际变化的模拟能力。得到以下结论：

(1)17个CMIP5气候模式对北半球夏季阻塞频数气候态的模拟存在不同程度的偏差，但与再分析场的相关系数均达到了0.5以上，总体而言各模式均能较好的模拟出夏季北半球气候态阻塞的空间分布，CanESM2的模拟结果最优，与再分析场的空间相关系数达到0.9257；CMCC-CESM和MIROC-ESM的模拟效果最差，空间相似系数仅为0.5155和0.6057；多模式集成的结果优于大多数单一模式，与NCEP/NCAR的相似程度达到0.8982。通过模式之间标准差分布可知，欧洲大陆30°E附近和北美洲西海岸(120°W)是模式间主要差异所在。

(2)与频数相比，CMIP5气候模式对于北半球夏季阻塞振幅的平均态的模拟能力稍弱。17个模式中，CanESM2同样可以最好的模拟出阻塞振幅的平均态特征，与再分析场的空间相关系数达到0.9027；同样是CMCC-CESM和MIROC-ESM的模拟效果最差，空间相似系数仅为0.5408和0.5820；多模式集合的结果为0.8011，仍然优于大多数单一模式的模拟能力。东北太平洋和东北大西洋这2个区域模式之间振幅的标准差最大，即这2个区域阻塞振幅模拟结果的差异是模式之间的主要区别所在。由动力学角度分析可知，西风急流、风暴轴和定常波是控制阻塞系统的重要因素，只有提高以上3个因素空间位置和强度的模拟能力，才可将阻塞的活动中心和强度显著区域做到成功模拟。

(3)没有任何一个模式可以同时正确的模拟出欧亚3个关键区1951—2005年的线性趋势。这说明对于夏季阻塞频数年际变化趋势的模拟，CMIP5气候模式的能力有限。

(4)大多数模式可以正确的模拟出欧亚3个关键区夏季平均阻塞频数和年际之间的标准差，其中乌拉尔山区由于本身夏季阻塞发生次数较少，因而模式之间的差异最小，且与观测场之间的偏差也最小。

(5)由NCEP/NCAR再分析场可见，1951—2005年欧洲区不存在夏季阻塞频数的主周期，乌拉尔山区存在有8年左右的主周期和2年左右的周期振荡，鄂霍茨克海区的周期为5.5年。17个CMIP5模式中，没有任何一个模式可以同时正确的模拟出欧亚3个关键区的主周期，这说明对于夏季阻塞频数的周期变化，模式的模拟能力同样有限。

综上所述，尽管CMIP5模式对北半球夏季阻塞频数和振幅的模拟存在偏差，但大部分模式可以很好模拟出气候平均态特征，且模式对频数的模拟结果稍优于振幅。无论频数或者振幅，CanESM2均为17个气候模式中模拟效果最好的，CMCC-CESM和MIROC-ESM的模拟效果最差，多模式集成的结果优于大部分单一模式。目前，已有研究发现：数值模式对于阻塞系统模拟能力依赖于模式本身的分辨率[14]，过低的水平分辨率有可能导致瞬变涡旋在阻塞发生发展过程中的作用无法体现[20]。由表1和模式模拟结果对比可知，一些高分辨率模式对夏季气候态阻塞频数(如CMCC-CM和MIROC5)和振幅(如MIROC5)的反演结果确实较好，但CMCC-CESM和IPSL-CM5A-LR虽然分辨率较低，却能较好的模拟出欧洲区阻塞的线性趋势。这或许说明提高数值模式对于阻塞的模拟能力，不仅仅依赖于提高模式的分辨率，还存在有更多的途径。

阻塞系统是北半球夏季中高纬度环流的重要组成部分。本文的结果为CMIP5模式对夏季气候平均态阻塞的频数和振幅模拟能力提供依据，同时为认识欧亚大陆3个关键区(欧洲区、乌拉尔山区和鄂霍次克海区)阻塞频数的线性趋势和年际变化特征提供参考。由于北半球夏季阻塞对中国的天气、气候存在重要影响，因此本文的研究对认识我国夏季气候的年际变化特征存在参考意义。

[1] Garriott E B. Long-range weather forecasts [M]. Washington, D. C: Government Printing Office, 1904.

[2] 陶诗言, 倪允琪, 赵思雄, 等. 1998年夏季中国暴雨的形成机理与预报研究 [M]. 北京: 气象出版社, 2001.

[3] Grumm R H. The central European and Russian heat event of July-August 2010 [J]. Bull Amer Meteor Soc, 2011, 92: 1285-1296.

[4] Berggren R, B Bolin, Rossby C G. An aerological study of zonal motion, its perturbations and break-down[J]. Tellus, 1949, 2: 14-37.

[5] Austins J F. The blocking of middle latitude westerly winds by planetary waves [J]. Quart J Roy Meteor Soc, 1980, 106: 327-350.

[6] 罗德海. 大气中大尺度包络孤立子理论与阻塞环流[M]. 北京: 气象出版社, 1999.

[7] Charney J G, Shukla J, Mo K C. Comparison of a barotropic blocking theory with observation [J]. J Atmos Sci, 1981, 38: 762-779.

[8] Dole R M, Gordon N D. Persistent anomalies of the extra-tropical Northern Hemisphere wintertime circulation: Geographical distribution and regional persistence characteristics [J]. Mon Wea Rev, 1983, 111(8): 1567-1586.

[9] Lejenäs H, Økland H. Characteristics of Northern Hemisphere blocking as determined from a long time series of observational data [J]. Tellus, 1983, 35A: 350-362.

[10] Tibaldi S, Molteni F. On the operational predictability of blocking [J]. Tellus, 1990, 42A: 343-365.

[11] Pelly J L, Hoskins B J. A new perspective on blocking [J]. J Atmos Sci, 2003, 60: 743-755.

[12] Diao Y, Li J, Luo D. A new blocking index and it s application: Blocking action in the Northern Hemisphere [J]. J Climate, 2006, 19: 4819-4827.

[13] Pelly J L, Hoskins B J. How well does the ECMWAF Ensemble Prediction System predict blocking? [J]. Quart J Royal Met Soc, 2003, 129: 1683-1702.

[14] Matsueda M. Blocking Predictability in operational medium-range ensemble forecast [J]. SOLA, 2009, 5: 113-116.

[15] D’Andrea F, Tibaldi S, Blackburn M, et al. Northern Hemisphere atmospheric blocking as simulated by 15 atmospheric general circulation models in the period 1979-1988 [J]. Climate Dyn, 1998, 14: 385-407.

[16] Barnes E A, Slingo J, Woolings T. A methodololgy for the comparison of blocking climatologies indices, models and climate scenarios [J]. Climate Dyn, 2012, 38: 2467-2481.

[17] Taylor K E, Stouffer R J, Meehl G A. An Overview of CMIP5 and the experiment design [J]. Bull Amer Meteor Soc, 2012, 93: 485-498.

[18] 余锦华, 唐盛, 吴立广, 等. IPCC AR4模式对热带气旋热力控制因子的模拟能力评估 [J]. 海洋学报, 2011, 33(6): 39-54.

[19] Masato G, Hoskins B, Woollings T. Winter and Summer Northern Hemisphere blocking in CMIP5 models [J]. J Climate, 2013, 26(18): 7044-7059.

[20] Ringer M A, Martin G M, Greeves C Z. The physical properties of the atmosphere in the new Hadley Centre Global Environmengt Model(HadGEM1). PartⅡ: Aspects of variability and regional climate [J]. J Climate, 2006, 19(7): 1302-1326.

[21] Lejenäs H. Long term variation of atmospheric blocking in the Northern Hemisphere [J]. J Meteor Soc Japan, 1995, 73: 79-89.

[22] 马丽娟, 罗勇, 秦大河, 等. CMIP3模式对未来50a欧亚大陆雪水当量的预估 [J]. 冰川冻土, 2011, 33(6): 707-720.

[23] 刁一娜, 李建平, 罗德海. 阻塞流场与瞬变涡动相互作用的动力学研究 [J]. 大气科学, 2004, 28(6): 901-924.

[24] 郭岩, 陈海山, 张宏芳, 等. CMIP3气候模式对东亚冬季大气环流模拟能力的评估 [J]. 气象与减灾研究, 2012, 35(1): 7-16.

[25] Li S, Ji L, Lin W, et al. The Maintenance of the Blocking over the Ural Mountains during the Second Meiyu Period in the Summer of 1998 [J]. Advances in Atmosheric Science, 2001, 18(1): 87-105.

责任编辑 庞 旻

Assessments on Simulation of Summer Northern Hemisphere Blocking in CMIP5 Climate Models

WU Jing1,2, DIAO Yi-Na1, ZHUANG Xu-Zong2

(1. Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China; 2. Ocean Hydrometeorology Institute, Navy Donghai-Armada, Ningbo 315100, China)

Based on the National Centers for Environmental Prediction/National Center for Atmospheric Research(NCEP/NCAR) gridded reanalysis data during 1951-2005 and model outputs from 20thCentury Climate Simulation experiment by 17 coupled models of the fifth phase of the Coupled Model Intercomparison Project (CMIP5), the capabilities of the climate models in simulating summer Northern Hemisphere blocking have been evaluated. In addition, the abilities of the models to simulate the linear tendency and interannual variability of summer frequency in the three key regions of Eurasia (Euro region, Ural Mountain region and Okhotsk region) are evaluated. Results show that : (1) Despite bias exists in 17 model results, the basic spatial patterns of the climatology of frequency and amplitude are well simulated. On the whole, the simulation of frequency is better than that of amplitude and the multi-model-ensemble (MME) shows better skill than most of single model. For both frequency and amplitude, CanESM2 is best and CMCC-CESM and MIROC-ESM are worst. (2) Most models can basically reproduce the climatology frequency and standard deviation in the three key regions of Eurasia, however, they fail to capture the linear tendency and interannual variability.

CMIP5； summer blocking； model evaluation

国家自然科学基金青年基金项目(40905030)；国家重点基础发展规划项目(2012CB417403)资助

2013-05-14；

2013-10-29

吴 静(1986-)，女，硕士生。E-mail：303120111@qq.com

❋❋ 通讯作者： E-mail:diaoyh@ouc.edu.cn

P462.4

A

1672-5174(2015)02-018-13

10.16441/j.cnki.hdxb.20130225