RV 针摆传动齿面接触强度非线性分析

吴素珍，何卫东

(1．大连交通大学 机械工程学院，辽宁 大连116028;2．河南工程学院 机械工程学院，河南 郑州451191)

0 引言

RV 减速器是一种两级行星减速传动机构，主要由第1 级渐开线行星传动和第2 级摆线针轮行星传动组成［1］，第2 级摆线轮与针轮的啮合工作性能，直接影响到整个减速器的工作精度．国内学者大部分是对直齿轮或斜齿轮的接触分析［2-5］，对摆线针轮啮合接触分析研究比较少，即使有一些相关的研究，但做了相当多的简化，如重庆大学的陈兵奎进行了摆线包络行星传动接触有限元分析及系统开发，其简化了摆线轮的内部结构［6］;大连交通大学的关天民进行了FA 型针摆传动齿面接触状态的有限元计算，其把针摆啮合简化成了二维模型［7］． 笔者考虑摆线轮修形量、轮齿接触变形等的影响，进行了针轮和摆线轮接触非线性应力应变分析．

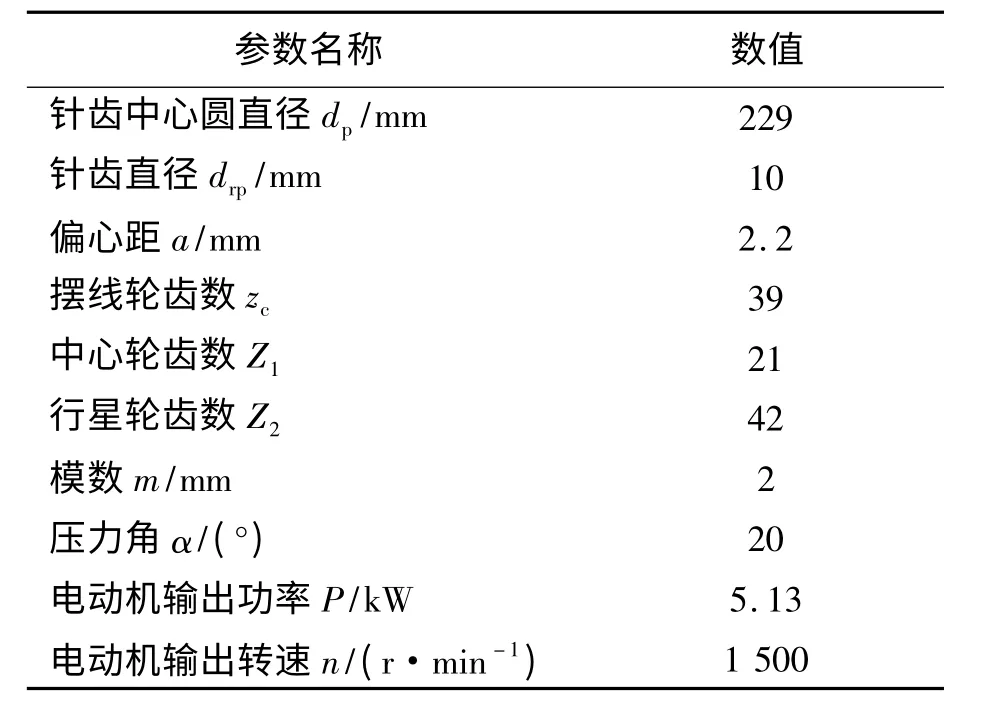
表1 RV－250 机型的相关参数Tab．1 Associated parameters of RV－250

1 摆线轮齿面数学模型

1．1 相关参数

笔者以RV-250 为例进行摆线轮针轮齿面接触状态的接触应力计算及有限元分析，其相关参数如表1 所示［8］．

1．2 摆线轮齿形方程

根据摆线针轮传动的啮合原理，以摆线轮的几何中心为原点，通过原点并与摆线轮对称轴重合的轴线为xc轴，考虑修形量的摆线轮齿形方程式为［9］:

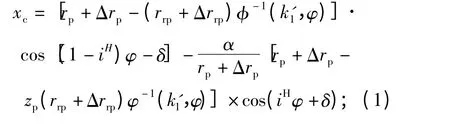
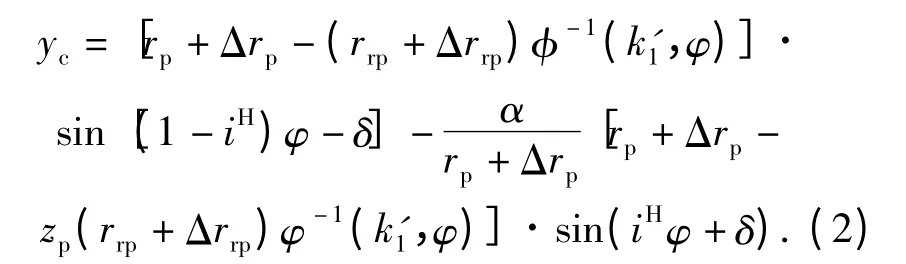
式中:k'1为有移距时齿形的短幅系数，iH为摆线轮和针轮的相对传动比，iH=zp/zc;其他参数见表1．

2 理论计算

2．1 针齿与摆线轮的作用力计算

标准齿廓时，针齿的接触力与该齿的变形成正比． 但在实际计算中，由于必须先克服初始间隙，此时针齿的接触力Fi应与变形和初始间隙之差(δi-Δ(φi))成线性正比关系，按照此关系，同时啮合传力的第i 个齿受力Fi可用式(3)表示．Fi=CiωPii=Ci［δi-Δ(φi)］Pi． (3)式中:Fi为各接触点φi处的针齿接触力;Ci，Pi为计算系数;δi为摆线轮各啮合点在公法线方向的总变形;Δ(φi)为初始法向啮合侧隙．

设摆线轮上的扭矩TC由i =m1～m2个齿传递，它应与针齿上各针齿给摆线轮作用力所产生的力矩平衡，由此可得:

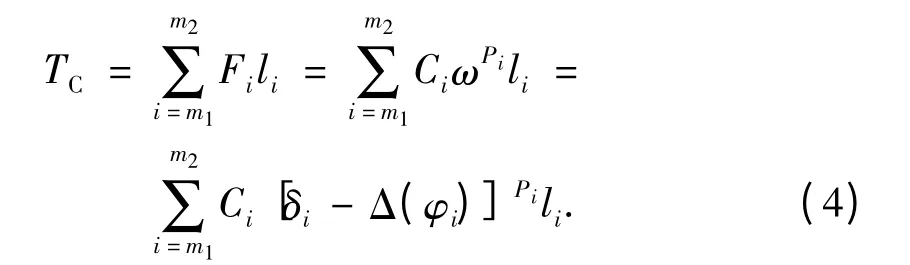
通过计算机搜寻可求解出在转矩TC作用下的同时啮合的齿数m1～m2，以及各接触齿上的作用力Fi，计算结果如表2 所示［8］．

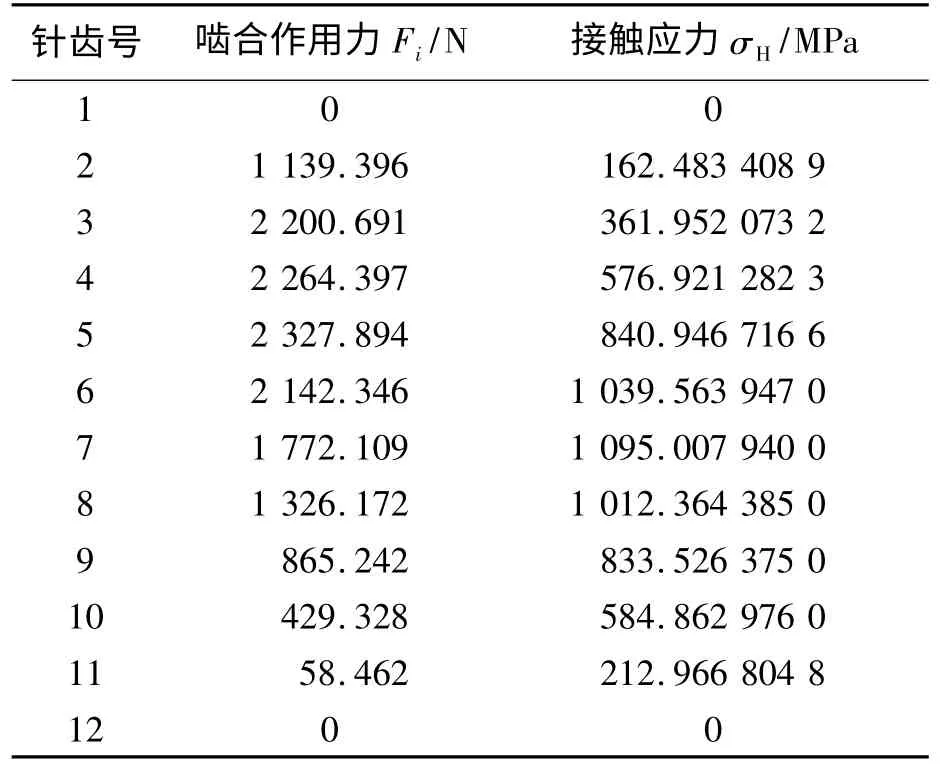
表2 摆线针轮啮合作用力、接触应力Tab．2 Acting force and contact stress chart of cycloid pin gear messing

2．2 摆线轮与针齿接触应力计算

根据赫兹公式，摆线针轮齿面接触应力为［8］:

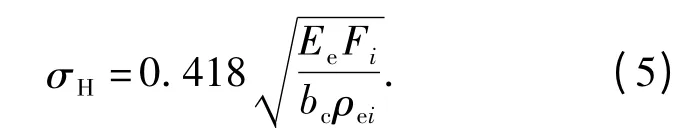
式中:Fi为针齿与摆线轮齿在某一位置啮合的作用力，N;Ee为当量弹性模型，MPa，Ee=2．06 ×105MPa;bc为摆线轮的宽度，mm;ρei为当量曲率半径，mm;ρi为摆线轮在某啮合点的曲率半径，mm．

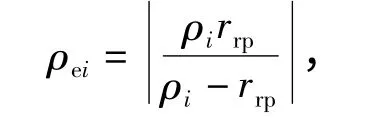
摆线针轮接触应力计算结果，如表2 所示．

3 模型建立

3．1 几何模型建立

RV 针摆减速器是精密传动减速器，对建模精度要求比较高，因此建模曲线误差在0．1 μm以下．摆线轮的结构在圆周上是每120°对称的，因此对120°范围内的13 个齿的啮合位置进行了计算．另外，针摆传动中，针齿是半埋在针齿壳的针齿销孔内，其弹性变形主要是接触变形，同时两片摆线轮与针齿的啮合完全一样，所以建模时简化了针齿壳且只保留了一片摆线轮，另外使针齿长度和一片摆线宽度相等，所建模型如图1 所示．

图1 摆线针轮传动模型Fig．1 Cycloid pin gear transmission model

3．2 有限元模型建立

摆线针轮传动是多齿接触受力的问题，实际工况中针齿与针齿壳之间的接触对摆线针轮接触分析结果影响比较小，所以把针齿壳和针齿看成了一个整体．建立有限元模型时另一关键的是单元类型的选择，这些单元类型有不同的拓扑结构和属性．在不同的单元类型中，实体单元能够模拟的结构最多，而且该小块材料的几何形状、节点数等可以有多种选择，并可在任何节点上与其它单元连接，因此几乎能承受任意载荷，所以在针摆有限元分析中选择了“solid185”单元，solid185 单元适用于构造三维固体结构，有8 个节点，每个节点有3 个沿着XYZ 方向平移的自由度，具有超弹性，蠕变，大变形和大应变能力．针齿和摆线轮材料均为GCr15，即定义的弹性模量为2． 06E5 MPa，泊松比为0．3，密度为7．8E12 kg/mm3．

摆线轮齿廓是一种精度极高的特殊曲线，所以摆线轮齿廓处和针齿啮合部分选用了较小的网格为0．6 mm，网格类型为混合四面体六面体．划分后的有限元模型如图2 所示，摆线轮针齿细密处网格如图3 所示． 本模型共形成965 314 个节点，880 512 个单元．

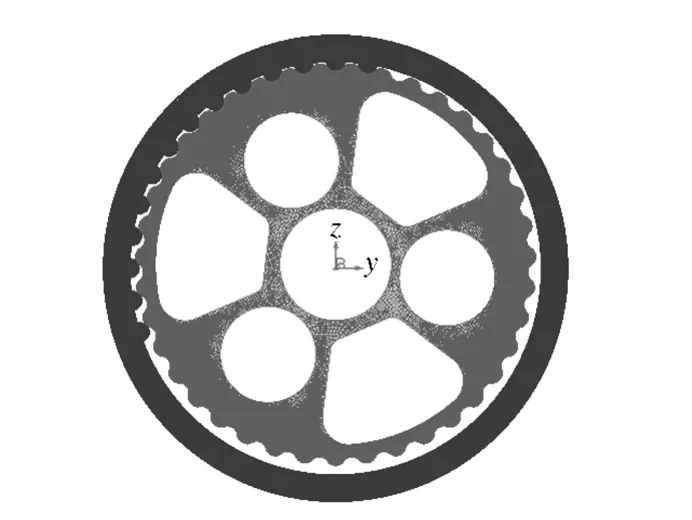
图2 摆线针轮啮合有限元模型Fig．2 Meshing FEM of cycloid pin gear

图3 摆线轮针齿细密处网格Fig．3 Close FEM meshes of cycloid and pin gear tooth

3．3 针轮与摆线轮接触对的定义

理论分析结果显示，经过修形的摆线轮与针齿在啮合受力前是1 个齿啮合，受力后摆线轮针齿为10 个齿啮合．为了有限元计算方便，需摆针轮有限元模型中有可能接触的齿需提前处于啮合状态，即需在此10 个齿间建立接触对．

摆线轮和针齿的材料相同，定义为柔体对柔体的面面接触．创建接触对时一般选择凸面为接触面，凹面为目标面．RV 针摆传动中针轮接触面为凸面，定义其为接触面，接触单元为CONTA173，摆线轮的接触面为凹面，定义其为目标面，目标单元为TARGE170，定义接触对时设置k5=1，忽略接触对的初始间隙，k9=1，忽略接触对的初始穿透，k10=2，允许ANSYS 自动更新接触刚度，k2=1，采用完全计分法计算，所建立的接触对局部放大图如图4 所示．

图4 摆线针轮接触对局部放大图Fig．4 Magnification of cycloid pin gear contact parts

4 边界条件和载荷的施加

研究摆线轮针齿传动某一瞬间齿面的接触状态，在瞬间，针轮和针齿壳是静止的，摆线轮公转相对速度很小，可以看成摆线轮只做绕偏心轴的自转．

在设置边界条件时，根据摆线针轮接触的实际工况，设置约束和加载条件．针齿壳刚性很大，并固定不动，即针齿壳施加完全约束;摆线轮带动行星架输出，采用3 个相连的刚性梁模拟行星架输出机构;刚性元模拟偏心轴曲柄，铰链链接技术模拟曲柄相对摆线轮轴承孔的转动，对轴承孔的约束模拟轴承和轴承孔的实际接触情况，对摆线轮偏心轴中心约束5 个自由度，只留一个绕偏心轴转动的自由度，模拟摆线轮绕偏心轴的转动，摆线针轮传动的约束边界条件如图5 所示．

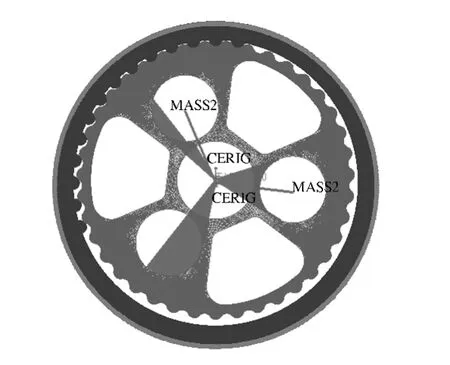
图5 边界条件的施加Fig．5 Applied boundary conditions

RV-250 的传动转矩T =2 450 N·m，由于制造误差，传递两个摆线轮的转矩是不相等的，一片摆线轮传递的扭矩一般取TC=0．55T =1 347．5 N·m．本模型施加的转矩为1 347．5 N·m．

5 结果分析

图6 所示为放大150 倍后的摆线轮接触应力云图，图7 为摆线轮各齿面的接触应力分布云图．有限元法计算的结果显示，摆线轮共10 个齿接触变形，最大接触应力出现在第7 个齿． 从图6 可以看出，摆线轮变形主要出现在接触区，并且轴承孔和梯形孔上方的齿出现了下沉变形，轮辐上方的齿出现了外凸变形． 原因是轮辐的结构比较单薄，摆线轮在齿面啮合力作用下产生变形，在啮合区域部分的变形比较明显，特别是梯形孔和轴承孔的部位由于齿缘很薄，刚度较小容易产生向内的下沉变形．而位于轮辐径向支承板近处齿的部分刚度较大，在摆线轮对针齿的作用力的作用下易产生外突的变形，如图7 中轮辐上方的3 个齿，通常受力最大;最大接触应力点在摆线轮齿面的内侧，说明有些边缘效应．

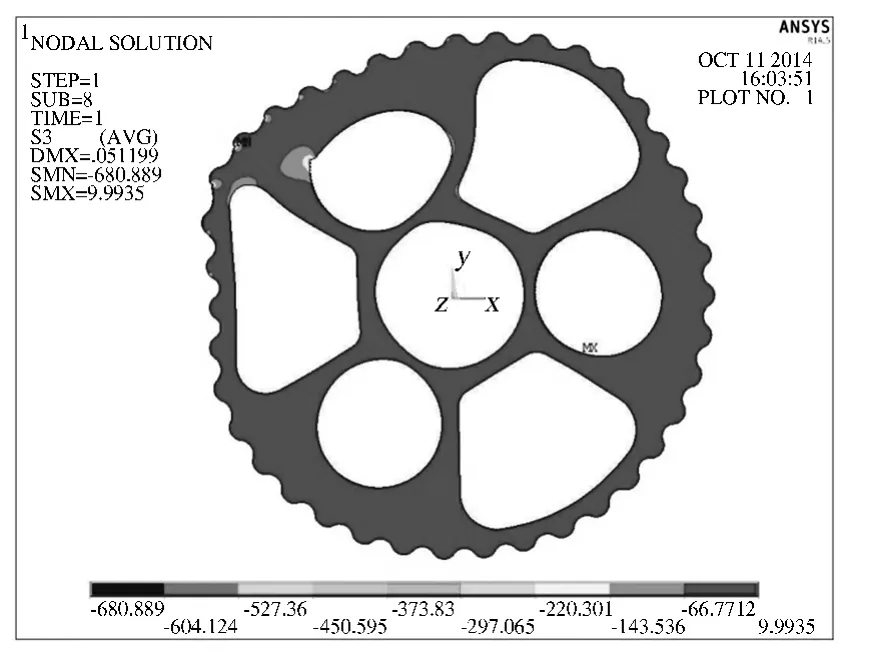
图6 摆线轮接触应力云图(放大150 倍)Fig．6 Stress contour of cycloid gear contact parts(magnified 150 times)

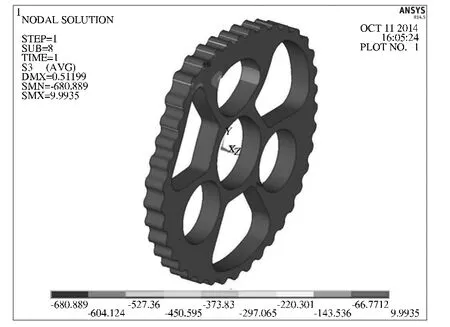
图7 摆线轮接触压应力云图Fig．7 Compressive stress contour of cycloid gear contact parts

图8 为摆线针轮接触状态图，从图中可以看出，接触的每对齿都接触良好，并且齿向未出现偏载．

图9 为两种计算方法的接触应力对比． 有限元计算的最大齿面接触应力为-680．889 MPa，主要有3 个齿承受较大的载荷，都分布在刚性较大的部位，赫兹理论计算的最大接触应力为1 095．007 94 MPa，两者相差比较大的原因为赫兹理论未考虑非线性因素及摆线轮内部轴承孔和梯形孔的影响，但总体分布规律一致，与实际接触应力是相符的．

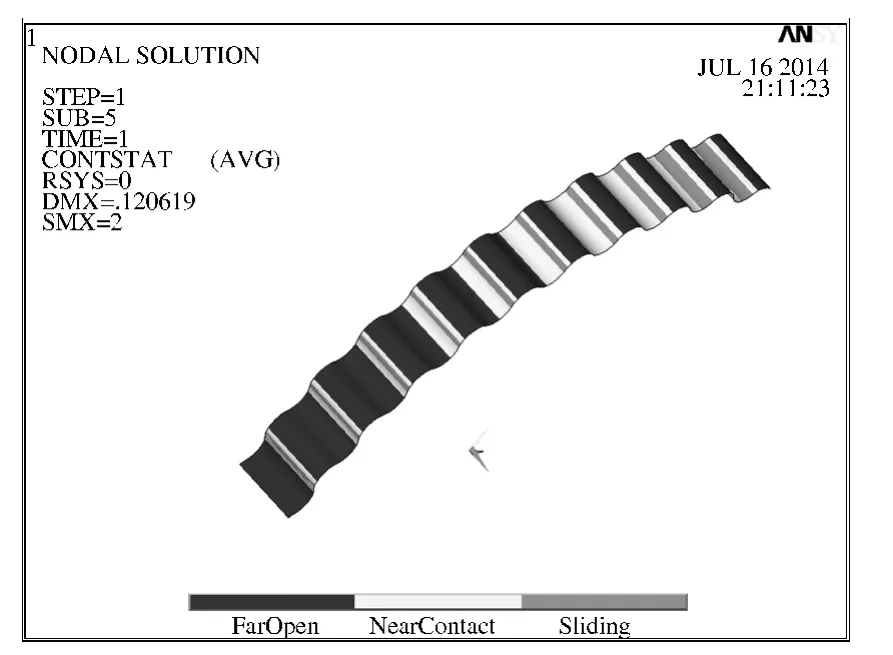
图8 摆线针轮接触状态图Fig．8 Statechart diagram of cycloid gear contact parts

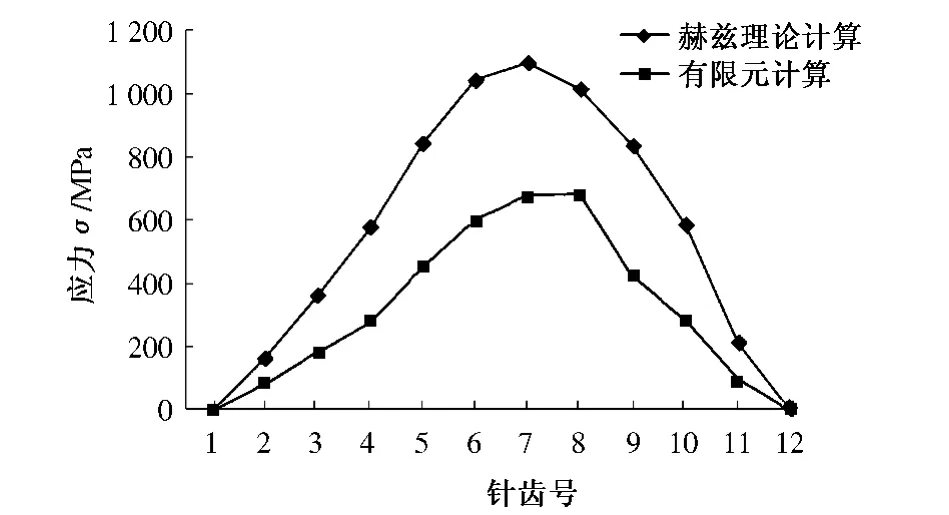
图9 两种分析计算结果比较Fig．9 The result analysis of the two motheds

6 结论

(1)赫兹理论和有限元法计算结果都有10个齿啮合，最大接触应力都发生在7 号齿，并且总体接触应力趋势是一致的，从而验证了所建有限元模型的正确性，为摆线轮的强度性能分析与评估提供可靠的数值依据．

(2)轮齿的接触状态和接触应力大小与变形情况有密切关系． 在梯形孔上方和轴承孔上方的齿的轮齿容易变形，承受的载荷较小，在刚性区辐板上方的齿承受的载荷较大．

(3)由于赫兹理论未考虑非线性因素及摆线轮内部轴承孔和梯形孔的影响，两种方法计算的接触应力存在一定的误差，但总体分布规律一致，与实际接触应力是相符的．

［1］ 何卫东，李欣，李力行．高承载能力高传动效率新型针摆行星传动研究［J］． 中国机械工程，2005，16(7):54 -57．

［2］ 唐进元，陈兴明，罗才旺．考虑齿向修形与安装误差的圆柱齿轮接触分析［J］．中南大学学报:自然科学版，2012，43(5):1703 -1709．

［3］ 王丹，路瑞成． 航空发动机齿轮接触分析与修形研究［J］．东北大学学报:自然科学版，2013，34(8):83-87．

［4］ 魏冰阳，陈金瑞． 小轮双鼓修形的面齿轮接触分析及试验［J］． 河南科技大学学报，2013，34(4):16-20．

［5］ 庞洪臣，廖红宜，杨杰华，等．联合收割机变速器齿轮接触分析［J］． 中国农机化学报，2013，34(3):30-35．

［6］ 陈兵奎，谭磊，钟晖，等．摆线包络行星传动接触有限元分析及系统开发［J］机械强度，2013，35(3):366 -371．

［7］ 关天民． FA 型摆线针轮行星传动齿形优化方法与相关理论的研究［D］． 大连:大连交通大学机械工程学院，2005．

［8］ 朱孝录．机械传动设计手册［M］．北京:电子工业出版社，2007:66 -72．

［9］ 何卫东．机器人用高精度RV 传动的研究［D］．哈尔滨:哈尔滨工业大学机电工程学院，1998．