交通荷载下斜坡加筋路堤动力特性研究

罗烈日，郑俊杰

(1．北京城建勘测设计研究院有限责任公司，北京100101;2．华中科技大学 土木工程与力学学院，湖北武汉430074)

0 引言

高速公路运营过程中，主要承受交通荷载作用，使道路产生沉降和不均匀沉降［1-3］．而目前对交通荷载的研究，主要将其模拟成静荷载，而交通荷载作为一种动荷载，其作用形式与作用效果与静荷载显著不同［4］．为真实反映交通荷载作用下路基受力和变形特性，近年来国内外一些学者开始将交通荷载作为动荷载进行针对性研究． 陈剑等［5］采用拟静力法分析动态数值问题，分别将交通荷载模拟为静荷载、移动恒定荷载和正弦波荷载，分析了交通荷载作用下路基土动力特性;刘少文等［6］采用数值模拟方法，研究了未加筋、加格栅和加EPS 板3 种工况下非对称路堤动力特性，刘飞禹等［7］通过建立桩承式加筋路堤三维动力模型，分析了桩间距、路堤高度、桩体模量等重要参数对路面沉降和路基孔隙水压力的影响;魏星等［8］基于试验变形监测结果，提出了一种描述交通荷载作用下软土残余变形发展经验模型，并以日本Saga 机场公路为例，证明了该公路软土路基沉降简化计算方法的有效性．但是，目前针对交通荷载的研究较少且缺乏系统性，尚未有交通荷载作用下斜坡加筋路堤的研究的报道．因此，为揭示交通荷载作用下斜坡加筋路堤动力特性，笔者采用数值模拟方法，在路堤顶面施加均布循环荷载，分析交通荷载作用下路堤变形的动力响应．

1 工程概况与数值模拟

以岢临(岢岚—临县)高速公路ZK115 +693断面斜坡路堤作为分析对象，路堤填方高度为39 m．采用阶梯形路堤边坡形式，当H ＜19 m 时，边坡比为1 ∶2;当H = 19 ～31 m 时，边坡比为1∶1．75;当H=31 ～39 m 时，边坡比为1∶1．5． 距路基顶面20 m 范围“满铺”10 层土工格栅以增加路堤整体稳定性，每层格栅间距2． 0 m． 采用FLAC3D 建立数值分析模型，模型左边界离路堤坡脚处40 m，右边界离路堤路肩处20 m，以减弱边界效应，地基8 m 深度处为基岩，物理力学参数见表1，数值模型几何尺寸如图1 所示．

表1 物理力学参数Tab．1 Physical and mechanical parameters

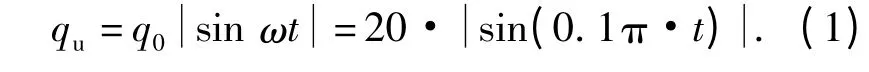
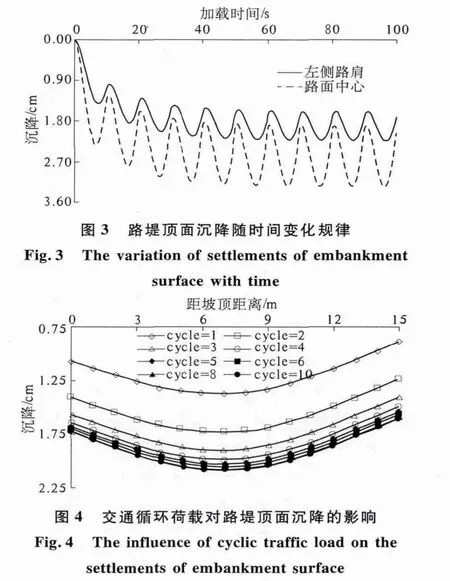
如图2 所示，采用半正弦波模拟路堤顶面交通荷载qu，qu均布作用在路堤顶面宽12 m 的路面范围内，其频率f 为0．1 Hz，振幅q0为20 kPa，t 为荷载作用的时间，qu的表达式见(1)式． 采用填筑完毕后的斜坡加筋路堤模型，将分级加载产生的速度场和位移场清零，忽略路面结构并考虑路面结构对交通荷载的均化作用，在路堤顶面施加动力均布荷载qu．至1．73 cm，增幅为0．35 cm;第8 次循环结束后路面最大沉降较第6 次循环仅增加了0．01 cm;当循环次数超过8 之后，路堤顶面沉降曲线几乎保持不变．图3 为前10 个循环周期路堤左侧路肩以及路面中心的沉降随加载时间的变化规律．从总体上看，在循环荷载qu作用下，沉降随加载时间大致呈半正弦波增加且逐渐趋于稳定． 在荷载作用初期(t＜T/2，T 为循环荷载周期)，沉降急剧增大，且t=T/2 时qu最大，左侧路肩及路面中心的沉降分别增大至1．16 cm 和2．10 cm;当T/2 ＜t ＜T 时，qu逐渐减小，沉降发生回弹，第一个荷载周期完成时，左侧路肩及路面中心沉降分别减小至1． 00 cm 和1．25 cm． 随着循环次数的增加，左侧路肩及路面中心沉降逐渐增大，但沉降增长的幅度逐渐减小．

图4 为不同循环次数时路堤顶面沉降曲线．由图可知，路堤顶面沉降呈先增大后减小的抛物线型变化，最大沉降出现在距坡顶6 ～7 m 处，且随着循环次数的增加，路堤顶面沉降逐渐增加，沉降曲线沿竖向坐标轴向下平移，但其增加的幅度逐渐减小．第1 次循环结束时，路堤顶面最大沉降约为1．38 cm;第2 次循环结束后，最大沉降增大

综上所述，交通循环荷载作用下，路堤顶面沉降随着荷载循环次数增加非线性增大，且沉降增加的幅度越来越小，当荷载循环次数超过某一定值之后，沉降趋于稳定．对于本例而言，当半正弦波交通荷载的频率f =0．1 Hz、振幅q0=20 kPa时，可认为循环次数达到8 次时路堤顶面沉降已达到稳定．

2 数值建模分析

2．1 交通循环荷载振幅的影响

改变荷载振幅大小，考虑q0分别为10，20，30 kPa 3 种工况下，交通循环荷载对斜坡路堤工作性状的影响，荷载频率f 为0．1 Hz．

图5 描述了q0对路面中心沉降变化的影响．由图5 可知，不同q0条件下，荷载作用时间t =8T时，路面中心的沉降基本趋于稳定;路面中心的沉降随着的q0增加逐渐增大，且q0越大，其变化幅度也越大．当q0分别为10，20 及30 kPa 时，t=T/2时路面中心的沉降分别为1．04，2．07 及3．11 cm，t=T 时路面中心的沉降分别为0．69，1．37及2．06 cm，路面中心沉降发生回弹的幅度分别为0．35，0．70 及1．05 cm，比较第1 次循环荷载作用下路面中心的沉降变化规律可知，路面沉降及回弹随q0增加大致呈线性增长．

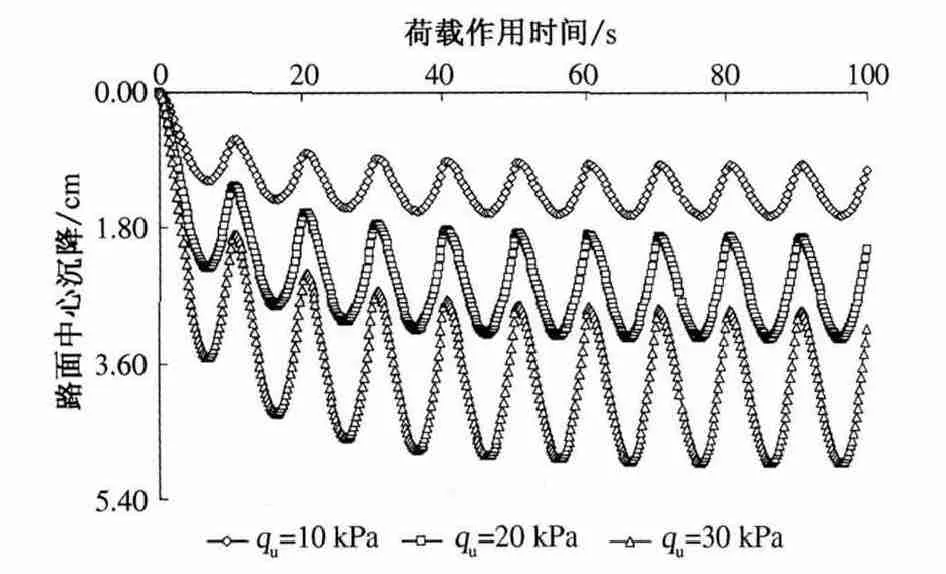
图5 交通循环荷载振幅对路面中心沉降的影响Fig．5 The influence of cyclic traffic load amplitude on the settlements of embankment surface center

2．2 交通循环荷载频率的影响

改变荷载频率，考虑f 分别为0．1，0．2 以及0．4 Hz 情况下，交通循环荷载对斜坡加筋路堤工作性状的影响，荷载振幅q0为20 kPa．

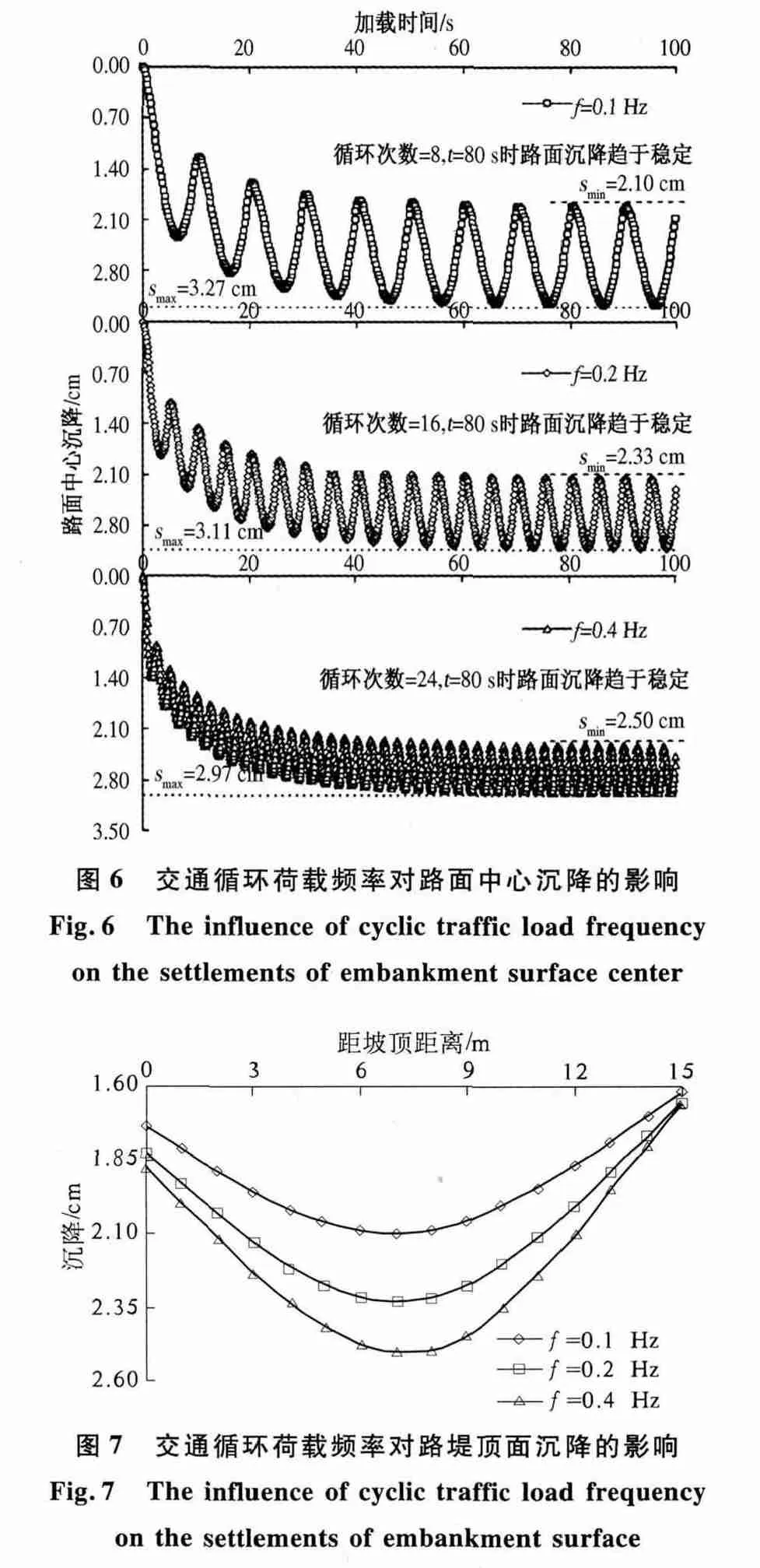
图6 描述了加载时间t =100 s 时，不同f 条件下，路面中心沉降随加载时间的变化规律．由图可知，随着f 的增大，荷载周期T 逐渐减小，交通荷载作用下路面中心最大沉降减小，且发生回弹的幅度降低．当f=0．1 Hz，T =10 s 时，循环次数达到8 次后，路面中心沉降变化基本趋于稳定，达到稳定状态后荷载循环过程中路面沉降的最小值为2．10 cm，最大值为3．27 cm，弹性变形为1．17 cm;当f=0．2，T=5 s 时，交通荷载循环次数达到16 次时，路面中心沉降变化基本稳定，沉降趋于稳定所需的加载时间仍为80 s，沉降趋于稳定后路面中心沉降的最小值和最大值分别为2．33 cm和3．11 cm，弹性变形为0．78 cm;当f =0．4 Hz，T=2．5 s 时，交通荷载循环加载24 次路面中心的沉降变化趋于稳定，达到稳定状态所需的加载时间t 为80 s，达到稳定状态后路面中心沉降的最小值为2．50 cm，最大值为2．97 cm，弹性变形为0．49 cm．因此，不同f 条件下振幅相同、交通循环荷载作用时，路面中心沉降趋于稳定时所需的循环次数随着f 呈倍数增加，但所需的加载时间t 基本保持不变，对于本例而言，t 约为80 s;当f 由0．1 Hz 增大到0．4 Hz 时，路面中心沉降变化达到稳定后，其最大值逐渐减小，最小值逐渐增大，弹性变形由1．17 cm 减小至0．49 cm．

图7 描述了t=300 s 时，交通循环荷载频率f对路面沉降的影响． 由图可知，不同f 条件下，路堤顶面沉降呈先增大后减小的抛物线型变化，在距坡顶7 m 处沉降最大，且随着f 的增加，沉降逐渐变大．当f=0．1 Hz 时，路堤顶面沉降的最大值和最小值分别为2．10 及1．62 cm，其变化幅度为0．48 cm;当f =0．2 Hz 时，路堤顶面最大沉降为2．33 cm，较前者增加了约0．23 cm，最小沉降为1．66 cm，沉降的变化幅度为0．67 cm;当f 增大至0．4 Hz 时，路堤顶面最大沉降增加了约0．17 cm，最小沉降几乎保持不变，沉降变化的范围由0．67 cm 增大至0．84 cm．因此，路堤顶面沉降随着f 的增大而逐渐变大，且其变化幅度也越来越明显．

2．3 交通循环荷载行车间隔的影响

假设车辆通过路堤横断面的时间为1 s，车辆荷载以半正弦波的形式均布作用在宽度为12 m的路堤顶面范围内，其振幅为20 kPa，假设连续两辆车通过同一断面的行车间隔为Δt，则循环荷载的周期T 为(1 +Δt)s，考虑T 分别10，20 和30 s，即Δt 分别为9，19 和29 s 3 种工况下斜坡路堤的工作性状，交通荷载qu随加载时间t 的变化规律如式(2)及图8 所示．

图9 为T=10 s，Δt =9 s 时，路面中心的沉降随加载时间的变化规律．由图可知，当nT≤t≤nT+1(n=0，1，2…)时，交通荷载呈半正弦波变化，路面中心的沉降随t 先增大后减小，且当qu=20 kPa 时，沉降最大;当nT+1≤t≤(n +1)T(n =0，1，2…)时，qu=0 kPa，路面中心沉降继续减小，但减小的幅度逐渐降低，沉降趋于稳定;随着交通荷载循环次数的增加，路面中心沉降逐渐增大，但增加的幅度越来越小，沉降逐渐趋于稳定．

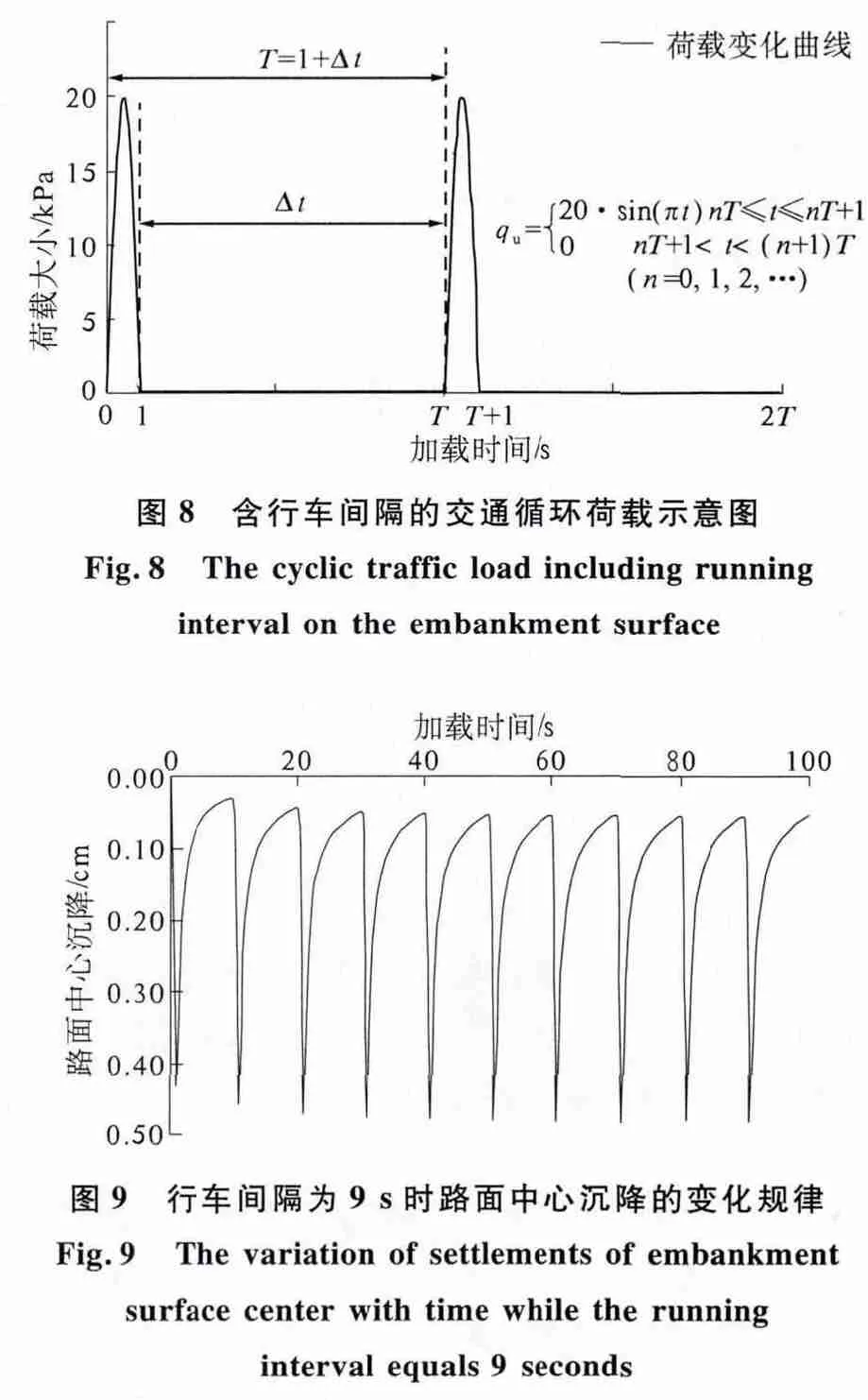
表2 不同行车间隔时沉降与循环次数的关系Tab．2 The relationship between settlements and cycle number under different running interval cm

表2 为不同行车间隔时，沉降与循环次数的关系．由表2 可知，Δt 越大，路面中心沉降达到稳定状态所需的循环次数越少，且达到稳定状态时的沉降越小．当Δt 分别为9，19 及29 s 时，路面中心沉降变化趋于稳定所需的循环次数分别为9 次、4 次及2 次．图10 为第20 次循环时不同行车间隔下路面中心沉降变化规律．由图10 可知，当Δt=9 s 时，路面中心沉降变化达到稳定时其最大值和最小值分别为0．48 cm 及0．05 cm，其弹性变形为0．43 cm;当Δt=19 s 时，路面中心沉降的最大值和最小值分别减小了0．04 cm，弹性变形仍为0．43 cm;随着Δt 的继续增大，循环荷载作用下路面中心沉降继续减小，但路面中心的弹性变形保持不变．因此，Δt 不同、振幅和频率相等的交通循环荷载引起路面中心的弹性变形约为0．43 cm，其塑性变形即最终沉降随着Δt 的增大而减小．

图11 为不同Δt 条件下，交通循环荷载作用20 个周期之后路堤顶面的沉降变化曲线．由图11可知，随着Δt 的增大，路面沉降逐渐减小，且其变化越来越均匀．当Δt=9 s 时，路面沉降随着距左侧路肩距离的增加呈先增大后减小变化，其最大值和最小值分别为0．54 mm 和0．50 mm，其变化幅度为0．04 mm，而Δt 增大到29 s 时，路面沉降基本保持在0．07 mm．

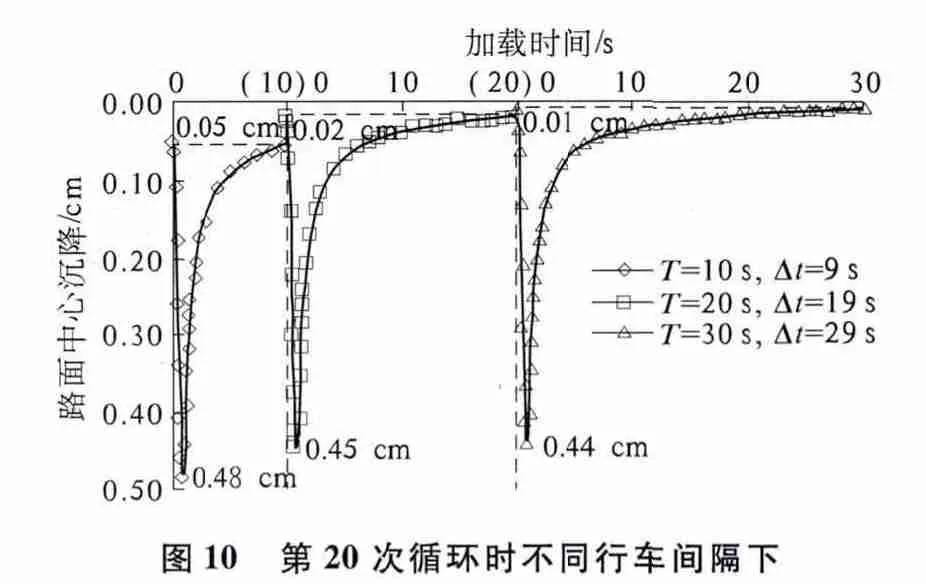
图10 第20 次循环时不同行车间隔下路面中心沉降变化规律Fig．10 The variation of settlements of embankment surface center under different running interval while cycle number is 20

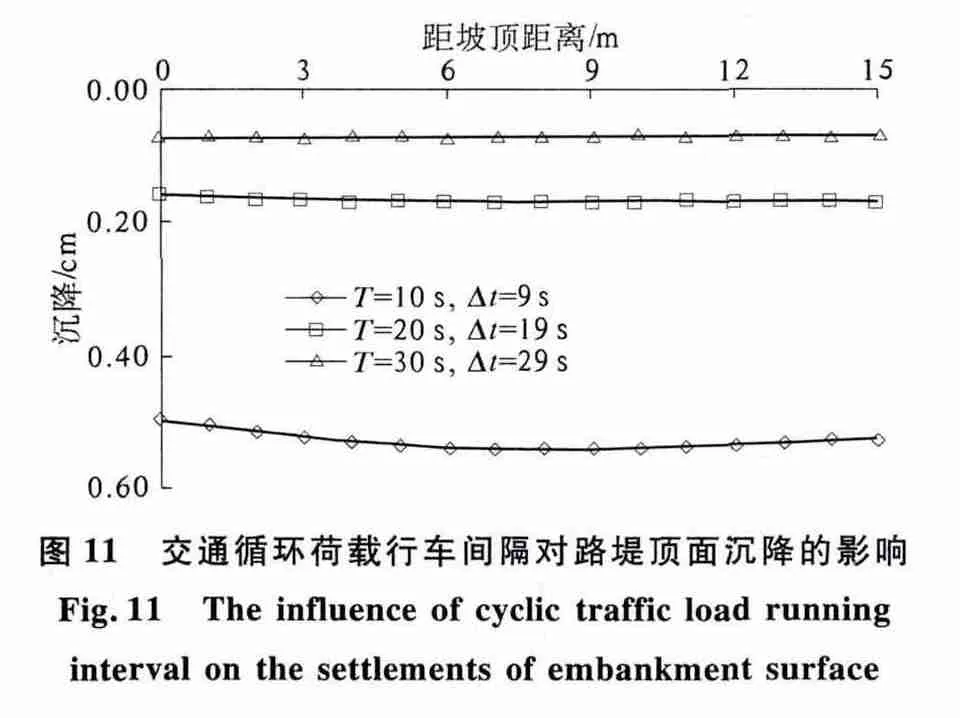
图11 交通循环荷载行车间隔对路堤顶面沉降的影响Fig．11 The influence of cyclic traffic load runninginterval on the settlements of embankment surface

3 结论

采用有限差分软件FLAC3D，建立了斜坡加筋路堤动力模型，在路堤顶面12 m 宽的范围内施加动力均布荷载，比较了荷载大小、荷载振幅和频率以及行车间隔对路面工作性状的影响，分析认为:

(1)半正弦波交通循环荷载作用下，路堤顶面沉降及水平位移变化较均匀． 随着循环次数的增加，路堤顶面沉降逐渐变大，直至趋于稳定，且达到稳定状态所需的加载时间基本不变．

(2)路堤变形稳定后，交通循环荷载振幅及频率越大，路堤顶面沉降变化越明显．

(3)考虑动力荷载行车间隔时，交通循环荷载引起斜坡加筋路堤的沉降很小．

［1］ SAKAI A，SAMANG L，MIURA N． Partially-drained cyclic behavior and its application to the settlement of a low embankment road on silty-clay ［J］． Soils and Foundations，2003，43(1):33 -46．

［2］ 刘飞禹，蔡袁强，徐长节，等． 移动荷载作用下加筋道路系统的动力响应［J］． 浙江大学学报:工学版，2007，41(1):57 -64．

［3］ 李进军，黄茂松，王育德． 交通荷载作用下软土地基累积塑性变形分析［J］． 中国公路学报，2006，19(1):1 -5．

［4］ 董忠红，吕彭民． 交通荷载下沥青路面结构动力响应理论研究［J］． 郑州大学学报:工学版，2007，28(4):88 -91．

［5］ 陈剑，苏跃宏． 交通荷载作用下公路路基动力特性的数值模拟研究［J］． 公路交通科技，2011，28(5):44 -48．

［6］ 刘少文，张军，孙玲． 交通荷载下非对称加筋路堤动力特性研究［J］． 郑州大学学报:工学版，2014，35(2):41 -45．

［7］ 刘飞禹，张乐，余炜，等． 交通荷载作用下桩承式加筋路堤性能分析［J］． 土木工程学报，2011，44(S2):50 -54．

［8］ 魏星，黄茂松． 交通荷载作用下公路软土地基长期沉降的计算［J］． 岩土力学，2009，30(11):3342 -3346．