传统压痕法识别陶瓷材料断裂韧性的有效性研究
王家梁,马德军,白盟亮,黄 勇,孙 亮
(1 装甲兵工程学院 机械工程系,北京 100072;2 总装备部西安军事代表局,西安 710065)
传统压痕法识别陶瓷材料断裂韧性的有效性研究
王家梁1,马德军1,白盟亮2,黄 勇1,孙 亮1
(1 装甲兵工程学院 机械工程系,北京 100072;2 总装备部西安军事代表局,西安 710065)
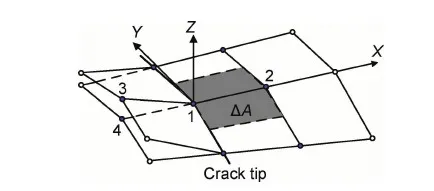
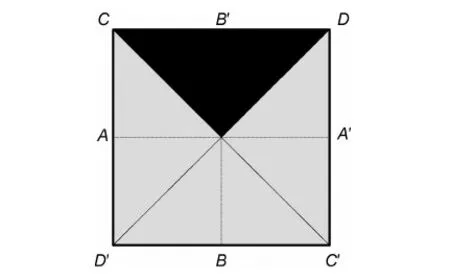
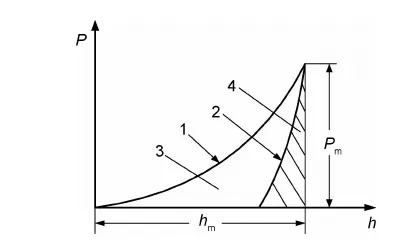
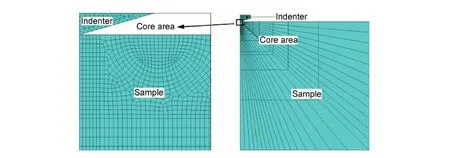
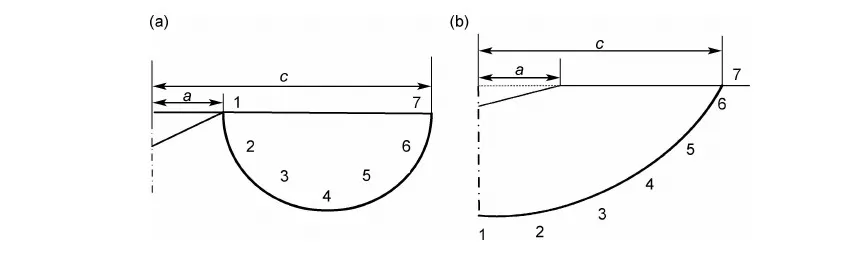
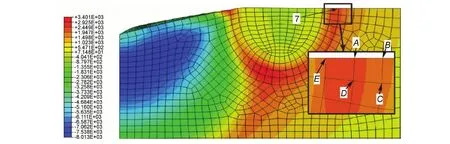
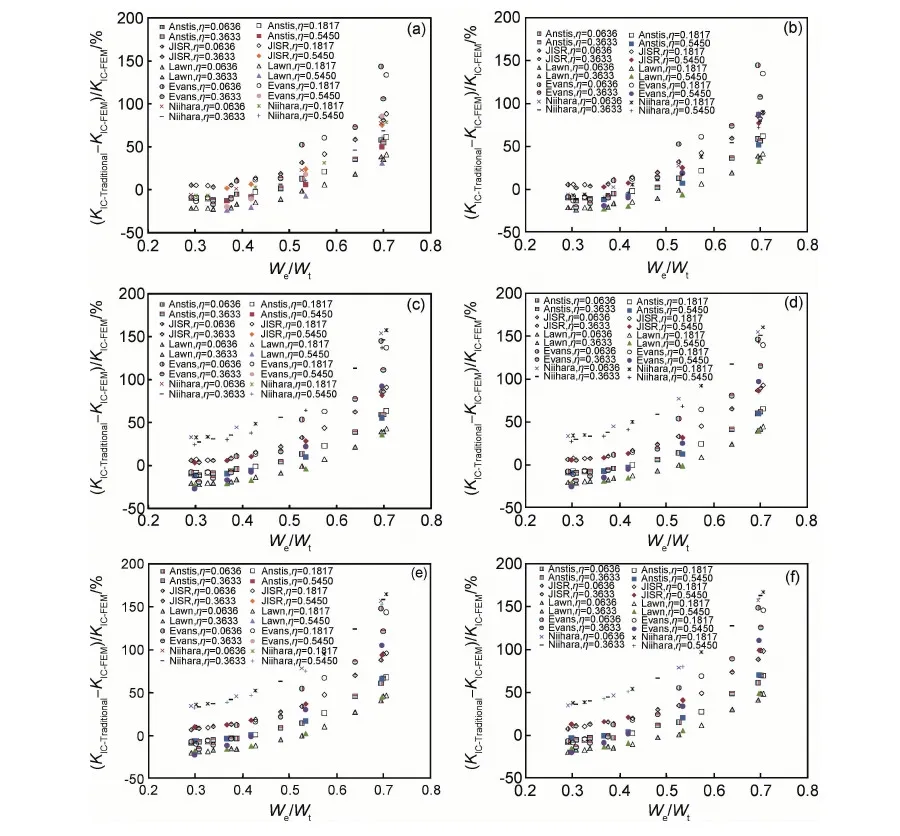
基于虚拟裂纹闭合法对传统压痕法测试陶瓷材料断裂韧性的数值模型进行计算,以此为基础,分析比较传统压痕法的几种典型公式识别陶瓷材料断裂韧性的测试误差和所测材料的适用范围。结果表明:传统压痕法的Anstis公式较Evans公式,Lawn公式,JISR公式和Niihara公式,在材料比功0.3≤We/Wt≤0.45时所测断裂韧性值与理论计算值较为接近,其最大误差为12.9%,测试结果相对准确;当0.45 传统压痕法;陶瓷材料;断裂韧性;虚拟裂纹闭合法;比功 对于陶瓷材料,其固有的脆性一直是制约其广泛应用的主要因素。作为衡量陶瓷脆性或韧性的重要力学性能指标——陶瓷材料断裂韧性KIC的准确测量一直是国内外研究人员广泛关注的核心和热点。目前,测试陶瓷材料断裂韧性的方法主要有表面裂纹弯曲法(Surface Crack in Flexure,SCF)[1,2]、山形切口梁法(Chevron-Notched Beam,CNB)[3,4]、单边预裂纹梁法(Single Edge Precracked Beam, SEPB)[5,6]、单边切口梁法(Single Edge Notched Beam, SENB)[7,8]和传统压痕法(Indentation Method, IM)[9-15]。考虑到应用的便捷性、效率、对试样尺度的要求等因素,IM法较SCF法、CNB法、SEPB法、SENB法具有明显优势,因而获得广泛应用。然而,由于传统压痕法的理论基础和公式建立系基于半解析与半经验方法的联合,因此,基于不同的实验结果所建立的经验公式可以因人和因实验而异,而已有的实验结果并不具有真值的特性。目前,常用的经验公式至少有五种之多,其他公式更是多达几十种,选择何种经验公式也是因人而异的。因此,传统压痕法存在诸多影响测试精度和应用方面的问题。 本工作基于虚拟裂纹闭合法[16]对传统压痕法测试陶瓷材料断裂韧性的有限元模型进行数值计算,从而得到不同材料的断裂韧性理论真值。以此为基础,分析比较传统压痕法的几种典型公式(Evans公式[9]、Lawn公式[10]、Anstis公式[11]、JISR公式[12]、Niihara公式[13])测试陶瓷材料断裂韧性的测试误差和所测材料的适用范围。从而为合理使用传统压痕法测试陶瓷材料断裂韧性以及建立测试精度高、适用范围广的断裂韧性测试新方法提供理论依据和技术基础。 1.1 虚拟裂纹闭合法的计算原理 虚拟裂纹闭合法(Virtual Crack Closure Technique,VCCT),由Rybicki和Kanninen于1977年提出,用于研究二维裂纹问题[16]。之后, Shivakumar等[17]把该方法延伸到面状裂纹问题。美国航天局兰利研究中心的Raju[18]首次对虚拟裂纹闭合法作出数学上的解释。近些年,Alan[19]、Xie等[20-22]和Qian等[23]对虚拟裂纹闭合法做了大量的研究工作。目前,在有限元分析断裂力学问题中被广泛用于计算材料的能量释放率G[24]。该方法的基本假设是虚拟裂纹尖端后侧的张开位移和实际裂纹尖端后侧的张开位移近似相等。因此,由虚拟裂纹闭合法的基本原理[25]可知,计算裂纹尖端处某一点的能量释放率,需要获取的有限元计算数据有裂纹尖端处的节点力FZ,裂纹尖端处后侧的节点位移w,裂纹尖端前侧的网格单元面积ΔA。8节点线性单元C3D8R示意图如图1所示。 图1 8节点单元的虚拟裂纹闭合法示意图Fig.1 Schematic diagram of virtual crack closure technique for 8 nodes element 3节点和4节点位于1节点的后侧,则Ⅰ型裂纹的应变能释放率GI可表示为 (1) 式中:FZ1为节点1沿Z轴的节点力;Δw3,4为节点3和节点4之间的相对位移。 1.2 有限元模型的建立 本工作通过仪器化压入仪[26,27]对陶瓷材料断裂韧性进行传统压痕法测试。因此,运用商用有限元软件ABAQUS建立基于Vickers压头的陶瓷材料断裂韧性仪器化压入有限元模型。考虑到标准的Vickers压头是面角为136°的正四棱锥,根据对称性取Vickers压头的1/4建模,同时被压材料也取与压头相对应的1/4模型,如图2所示。 图2 1/4对称的Vickers压头示意图Fig.2 Schematic diagram of the Vickers indenter 1/4 symmetry 假设被测材料为均匀、各向同性的率无关固体,且遵循Von Mises屈服准则及纯各向同性强化准则,同时材料的应力-应变关系由线弹性与Hollomon幂硬化函数组成,即 (2) 式中:E为弹性模量;σ为真实应力;ε为真实应变;εy为屈服应变;n为应变硬化指数;σy为屈服强度。仪器化压入加卸载曲线及加卸载功示意图如图3所示,纵轴表示压入载荷P,横轴表示压入深度h,加载曲线为1,卸载曲线为2,加载功Wt区域为3,卸载功We区域为4。其中,仪器化压入所设定的某一最大压入载荷为Pm,与之相对应的最大压入深度为hm。进一步定义仪器化压入加载功Wt和卸载功We分别为实施仪器化压入时金刚石Vickers压头在加载阶段和卸载阶段所做的功,其值分别等于加载曲线和卸载曲线与仪器化压入载荷-位移曲线横坐标所围面积。仪器化压入比功We/Wt为卸载功We与加载功Wt的比值[28]。 图3 仪器化压入加卸载曲线及加卸载功示意图Fig.3 Schematic diagram of the instrumented indentation loading-unloading curve and loading-unloading work 定义被压材料与金刚石Vickers压头的平面应变弹性模量之比η=[E/(1-0.22)]/[1141/(1-0.072)],被压材料的弹性模量E分别为70,200,400,600GPa,相应地η分别为0.0635,0.1817,0.3634,0.5451。考虑到绝大多数陶瓷材料比功We/Wt处于0.3到0.7之间,根据此比功We/Wt范围取相应的屈服强度值σy=1.4~30GPa。陶瓷为低硬化水平材料,应变硬化指数取n=0,泊松比取v=0.2,压头与被压材料间的摩擦因数取定值0.15。运用三维实体单元C3D4和C3D8R进行网格划分,采用减缩积分算法求解。在靠近压头尖端的区域(核心区)网格划分精细,远离压头的区域(非核心区)采用尺寸逐渐增大的网格单元,最终对压头划分了12000个C3D4单元,对被压材料划分了4500个C3D4单元和12000个C3D8R单元,网格划分后如图4所示。 图4 有限元模型的网格划分Fig.4 The mesh division of FEM 整个有限元分析过程分三步进行:第一步,压头压入的最大压入深度为hm;第二步,压头卸载至初始加载位置;第三步,被压材料沿压头对角线方向开裂,即裂纹面形成。对于被压材料沿压头对角线方向裂纹面的建模,可通过定义被压材料沿压头对角线截面的对称性实现,即裂纹面不按对称面设置,以刚性面限制其沿压头对角线截面法线方向的正位移,未开裂面仍按对称面设置。由于传统压痕法测试陶瓷材料KIC时,裂纹尖端处的KIC值均达到裂纹失稳扩展的临界值,假设被测陶瓷材料为均匀、各向同性的率无关固体,则裂纹尖端各处的KIC值均应相等。考虑到压痕法测试陶瓷材料断裂韧性过程中,被压材料将产生两种裂纹开裂形式,即径向裂纹开裂(Radial Crack,RC)和半硬币裂纹开裂(Half Penny Crack,HPC)[29,30]。因此,在有限元分析时使用接近实际开裂的等KIC值半椭圆形面(或1/4椭圆形面)作为裂纹开裂面,如图5所示,c为裂纹开裂半长。定义名义压痕对角线半长a为压头达到最大压入深度hm时对应的理论压痕对角线长度的一半。由Vickers压头的几何特征可知,a=3.5hm。建立裂纹开裂半长c与名义压痕对角线半长a之比c/a分别为1.25,1.5,2.25,3,4.5,6的六种模型。经研究发现,当c/a=1.25,1.5,2.25时,裂纹为RC开裂形式;当c/a=3,4.5,6时,裂纹为HPC开裂形式。 为了实现裂纹尖端等KIC值的要求,其基本步骤为:首先,假设Vickers压痕对角线方向的裂纹开裂面几何形状为半椭圆形,并在开裂面椭圆曲线上等距取5~7个节点作为参考节点(图5),分别计算其KIC值。 图5 传统压痕法测试陶瓷材料断裂韧性的两种裂纹开裂形式示意图 (a)RC开裂;(b)HPC开裂Fig.5 Schematic diagrams of traditional indentation method to determining the fracture toughness of ceramic materials (a)RC crack;(b)HPC crack 以RC裂纹开裂形式中“7”点为例(图6),获取A节点垂直裂纹面方向的节点力FZ1,E节点垂直裂纹面方向的张开位移Δw3,4,裂纹尖端前侧单元四边形ABCD面积的一半ΔA。 图6 RC裂纹开裂形式的有限元模型应力云图(垂直裂纹面的正应力)Fig.6 Stress contours of FEM for RC crack form (normal stress of vertical crack surface) 由式(1)计算得到“7”点处裂纹尖端的临界能量释放率GIC。平面应变状态下临界能量释放率GIC和断裂韧性KIC的关系式[31]: (3) 其次,根据各参考节点KIC值的大小对其位置进行调整,并通过样条曲线光滑连接调整后的参考节点形成新的裂纹开裂面几何形状。最后,计算调整后的参考节点KIC值,并重复上述过程直至各参考节点的KIC值相差不超过±5%,最终实现裂纹尖端的等KIC值要求。 (Anstis公式) (JISR公式) (Lawn公式) (Evans公式) (1.25≤c/a′≤3.5) (Niihara公式) (Niihara公式) 如果用KIC-Traditional表示基于上述5种经验公式计算所得断裂韧性结果,则传统压痕法计算KIC的理论误差为(KIC-Traditional-KIC-FEM)/KIC-FEM。图7(a)~(f)分别示出不同c/a及η下的基于传统压痕法计算KIC的理论误差(KIC-Traditional-KIC-FEM)/KIC-FEM与比功We/Wt的关系图。 图7 c/a=1.25~6时不同η下的 (KIC-Traditional-KIC-FEM)/KIC-FEM-We/Wt关系图 (a)c/a=1.25;(b)c/a=1.5;(c)c/a=2.25;(d)c/a=3;(e)c/a=4.5;(f)c/a=6Fig.7 Relationship between (KIC-Traditional-KIC-FEM)/KIC-FEM and We/Wt for c/a=1.25-6 and different η (a)c/a=1.25;(b)c/a=1.5;(c)c/a=2.25;(d)c/a=3;(e)c/a=4.5;(f)c/a=6 由图7的五种经验公式在材料比功0.3≤We/Wt≤0.45时的误差可知,当We/Wt=0.3~0.45时,Anstis公式,Evans公式,Lawn公式,JISR公式和Niihara公式所测断裂韧性值与理论计算值的最大误差分别为12.9%,27.2%,23.8%,20.8%和50.6%,其误差变化较为稳定。此时,传统压痕法的Anstis公式较Evans公式,Lawn公式,JISR公式和Niihara公式所测断裂韧性值相对准确。当0.45 实验选用的被压陶瓷材料为按照GB/T 21838.1-2008[34]要求制备的氮化硅(Si3N4)、氧化锆(ZrO2)、氧化锆增韧氧化铝 (ZTA)、氧化铝(Al2O3)以及熔融硅(fused silica)压入标准试样块。其中,Si3N4,ZrO2,ZTA,Al2O3试样由中国建筑材料科学研究总院陶瓷科学研究院制备,采用高纯超细粉料通过等静压成型方法制得,试样密度分别为3.21,6.02,4.28,3.95g/cm3,弹性模量分别为310,251,419,314GPa。fused silica试样为纳米压入仪用标准样品(GSB03-2496-2008),原料纯度≥99.9%,密度为2.20g/cm3,弹性模量为72GPa。应用先期获得国家发明专利授权的高精度仪器化压入仪[27]和金刚石Vickers压头对上述五种陶瓷材料进行仪器化压入实验,加载阶段和卸载阶段速率均为0.5N/s,保载时间为30s。考虑到不同压入载荷对被压材料压痕形貌的影响,对Si3N4,ZrO2,ZTA以及Al2O3试样,选用的最大压入载荷均为100N,而对于fused silica试样,选用的最大压入载荷为2N。为保证测试结果的准确性,每种材料实验重复进行10次,图8(a)~(e)分别为上述五种陶瓷材料的Vickers压痕及裂纹形貌图。 图8 五种陶瓷材料的Vickers压痕及裂纹形貌图 (a)Si3N4-100N;(b)ZrO2-100N;(c)ZTA-100N;(d)Al2O3-100N;(e)fused silica-2NFig.8 Topographies of Vickers indentation impression and crack morphologies for 5 kinds of ceramic materials (a)Si3N4-100N;(b)ZrO2-100N;(c)ZTA-100N;(d)Al2O3-100N;(e)fused silica-2N 对已进行了仪器化压入测试的试样,利用光学显微镜分别量取Vickers压痕实际对角线半长a′=(a1+a2)/2和Vickers压痕对角线方向上的裂纹开裂半长c=(c1+c2+c3+c4)/4,如图9所示,从而可以获得所压材料的仪器化压入测试结果,如表1所示。然后,根据传统压痕法测试陶瓷材料断裂韧性KIC的计算公式计算上述五种材料的断裂韧性值,结果列于表2。 从表2可以看出,除fused silica外,其余四种陶瓷材料的断裂韧性理论计算值KIC-FEM与Anstis公式测试值KIC-Anstis均较为接近,其原因可由图7(b)~(d)中(KIC-Traditional-KIC-FEM)/KIC-FEM-We/Wt的关系予以解释,当We/Wt≈0.4且c/a=2~3时,(KIC-Traditional-KIC-FEM)/KIC-FEM≈0,此时Anstis公式的计算精度最高,因此KIC-Anstis与KIC-FEM值最为接近, 其他公式计算结果与理论计算值差别相对较大;而对于fused silica材料,由于We/Wt=0.69,则同样从图7(a)中(KIC-Traditional-KIC-FEM)/KIC-FEM-We/Wt的关系可以看出,此时传统压痕法的断裂韧性计算结果均较有限元数值分析结果偏高约40%~140%,由此导致传统压痕法的断裂韧性计算结果(KIC-Anstis,KIC-Lawn,KIC-JISR,KIC-Evans及KIC-Niihara)较KIC-FEM值偏高约40%~140%。根据文献[35]所测silica材料的断裂韧性KIC值为0.798MPa·m1/2,与本文有限元模型利用虚拟裂纹闭合法计算得到的断裂韧性测试结果KIC-FEM=0.77 MPa·m1/2极为相近,而与传统压痕法所测结果KIC=1.08~1.87MPa·m1/2差别较大,从而验证了本文的结论,即传统压痕法对于比功We/Wt>0.45的陶瓷材料,断裂韧性测试值与理论计算值差别较大。同时,也进一步验证了本工作采用虚拟裂纹闭合法计算传统压痕法测试陶瓷材料断裂韧性模型结果的准确性。 图9 Vickers压痕及裂纹开裂半长示意图Fig.9 Schematic diagram of the Vickers indentation impression and crack half-length 表1 五种陶瓷材料的仪器化压入测试结果 表2 传统压痕法对五种陶瓷材料断裂韧性测试结果的比较(MPa·m1/2) (1)传统压痕法的Anstis公式较Evans公式,Lawn公式,JISR公式和Niihara公式在材料比功0.3≤We/Wt≤0.45时所测断裂韧性值与理论计算值较为接近,其最大误差为12.9%,测试结果相对准确可靠。 (2)当材料比功0.45 (3)虚拟裂纹闭合法对陶瓷材料断裂韧性的计算简洁、有效,该方法为下一步探索建立测试精度高、适用范围广的断裂韧性测试新方法提供了理论依据和技术基础。 [1] ASTM-C1421.Standard test methods for determination of fracture toughness of advanced ceramics at ambient temperature[S]. [2] ISO18756-2003.Fine ceramics (advanced ceramics, advanced technical ceramics) -determination of fracture toughness of monolithic ceramics at room temperature by the surface crack in flexure (SCF) method[S]. [3] ISO24370-2005.Fine ceramics (advanced ceramics, advanced technical ceramics) - test method for fracture toughness of monolithic ceramics at room temperature by chevron-notched beam (CNB) method[S]. [4] MUNZ D,BUBSEY R T,SHANNON J L. Fracture toughness determination of Al2O3using four-point-bend specimens with straight-through and chevron notches[J].J Am Ceram Soc,1979,63(5-6):300-305. [5] ISO15732-2003. Fine ceramics (advanced ceramics, advanced technical ceramics) -test method for fracture toughness of monolithic ceramics at room temperature by single edge precracked beam (SEPB) method[S]. [6] GB/T 23806-2009.精细陶瓷断裂韧性试验方法——单边预裂纹梁(SEPB)法[S]. [7] MA J, QI Q, BAYLEY J, et al. Development of SENB toughness measurement for thermoset resins[J].Polym Test,2007,26(4):445-450. [8] DAMANI R, GSTREIN R, DANZER R. Critical notch-root radius effect in SENB-S fracture toughness testing[J].J Euro Ceram Soc,1996,16(7):695-702. [9] EVANS A G, CHARLES E A. Fracture toughness determination by indentation[J]. J Am Ceram Soc,1976,59(7-8):371-376. [10] LAWN B R, EVANS A G, MARSHALL D B. Elastic/plastic indentation damage in ceramics: the median/radial crack system[J]. J Am Ceram Soc,1980,63(9-10):574-581. [11] ANSTIS G R, CHANTIKUL P, LAWN B R, et al. A critical evaluation of indentation techniques for measuring fracture toughness: I, direct crack measurements [J]. J Am Ceram Soc,1981,64(9):533-538. [12] JISR1607-1995. Testing methods for fracture toughness of high performance ceramics[S]. [13] NIIHARA K, MORENA R, HASSELMAN D P H. Evaluation ofKICof brittle solids by the indentation method with low crack-to-indent ratios[J]. J Mater Sci Lett,1982,1(1):13-16. [14] LANKFORD J. Indentation microfracture in the Palmqvist crack regime: implications for fracture toughness evaluation by the indentation method[J]. J Mater Sci Lett,1982,1(8):493-495. [15] LAUGIER M T. New formula for indentation toughness in ceramics[J]. J Mater Sci Lett,1987,6(3):355-356. [16] RYBICKI E F, KANNINEN M F.A finite element calculation of stress intensity factors by a modified crack closure integral[J]. Eng Fract Mech,1977,9(4):931-938. [17] SHIVAKUMAR K N, TAN P W, NEWMAN J C.A virtual crack-closure technique for calculating stress intensity factors for cracked three dimensional bodies[J]. Int J Fracture,1988,36(3):R43-R45. [18] RAJU I S. Calculation of strain-energy release rates with high-order and singular finite-elements[J]. Eng Fract Mech,1987,28(3):251-274. [19] ALAN T Z. Lecture notes on fracture mechanics[D].Ithaca,USA:Cornell University,2006. [20] XIE D, BIGGERS S B Jr.Strain energy release rate calculation for a moving delamination front of arbitrary shape based on the virtual crack closure technique, part I:formulation and validation[J]. Eng Fract Mech,2006,73(6):771-785. [21] XIE D, BIGGERS S B Jr.Strain energy release rate calculation for a moving delamination front of arbitrary shape based on the virtual crack closure technique, part II: sensitivity study on modeling details[J]. Eng Fract Mech,2006,73(6):786-801. [22] XIE D, BIGGERS S B Jr. Progressive crack growth analysis using interface element based on the virtual crack closure technique[J]. Finite Elem Anal Des,2006,42(11):977-984. [23] QIAN Q, XIE D. Analysis of mixed-mode dynamic crack propagation by interface element based on virtual crack closure technique[J]. Eng Fract Mech,2007,74(5):807-814. [24] KRUEGER R. Virtual crack closure technique: history, approach, and applications[J]. Appl Mech Rev,2004,57(2):109-143. [25] 解德,钱勤,李长安.断裂力学中的数值计算方法及工程应用[M].北京:科学出版社,2009. [26] 宋仲康.高精度压入仪设计与材料力学性能测试方法研究[D]. 北京:装甲兵工程学院,2010. [27] 马德军,宋仲康,郭俊宏,等.一种高精度压入仪及金刚石压头压入试样深度的计算方法[P].中国专利:102288500A,2011-12-21. [28] 马德军.材料力学性能仪器化压入测试原理[M]. 北京:国防工业出版社,2010. [29] PALMQVIST S. A method to determine the fracture toughness brittle materials, especially hard metals[J]. Jenkontorets Ann,1957,141(1):303-307. [30] TANG Y, YONEZU A, OGASAWARA N, et al. On radial crack and half-penny crack induced by Vickers indentation[J]. Proc R Soc A,2008,464(2099):2967-2984. [31] 赵建生.断裂力学及断裂物理[M].武汉:华中科技大学出版社,2003. [32] BOUZAKIS K D, MICHAILIDIS N, SKORDARIS G. Hardness determination by means of a FEM-supported simulation of nanoindentation and applications in thin hard coatings[J]. Surf Coat Technol,2005,200(1-4):867-871. [33] BOUZAKIS K D, MICHAILIDIS N. Indenter surface area and hardness determination by means of a FEM-supported simulation of nanoindentation[J]. Thin Solid Films,2006,494(1-2):155-160. [34] GB/T 21838.1-2008.金属材料硬度和材料参数的仪器化压痕试验第1部分:试验方法[S]. [35] WIEDERHORN S M. Fracture surface energy of glass[J]. J Am Ceram Soc,1969,52(2):99-105. Validity of Traditional Indentation Method for Evaluating Fracture Toughness of Ceramic Materials WANG Jia-liang1,MA De-jun1,BAI Meng-liang2,HUANG Yong1,SUN Liang1 (1 Department of Mechanical Engineering,Academy of Armored Force Engineering,Beijing 100072,China;2 Xi’an Military Representative Bureau,General Armament Ministry,Xi’an 710065,China) The numerical model of evaluating ceramics’ fracture toughness by traditional indentation method was calculated with the application of virtual crack closure technique, based on which, the measurement errors and application scope of several typical formulas employed in traditional indentation method to evaluate the fracture toughness of ceramic materials were analyzed. The results show that, compared with Evans formula, Lawn formula, JISR formula and Niihara formula of traditional indentation method, the value of fracture toughness measured by using Anstis formula is closer to the theoretical value, enjoying relatively accurate testing results with a maximum error of 12.9%, when the material’s ratio of unloading work to total loading work fell 0.3≤We/Wt≤0.45. When the material’s ratio of unloading work to total loading work ranged 0.45 traditional indentation method;ceramic material;fracture toughness;virtual crack closure technique;ratio of unloading work to total loading work 10.11868/j.issn.1001-4381.2015.12.014 TQ174.75 A 1001-4381(2015)12-0081-08 军内科研计划资助项目(2013ZBJ03) 2014-11-26; 2015-04-26 马德军(1964—),男,教授,主要从事材料力学性能仪器化压入测试方法的研究,联系地址:北京市丰台区长辛店杜家坎21号装甲兵工程学院机械工程系(100072),E-mail:dejunma@yahoo.com1 数值计算
2 结果分析
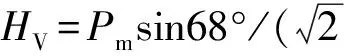
3 实验验证

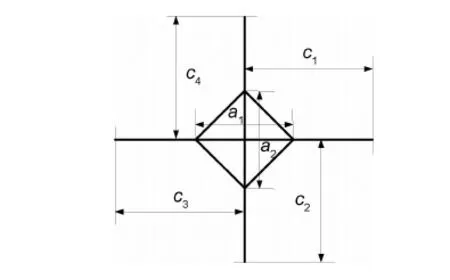

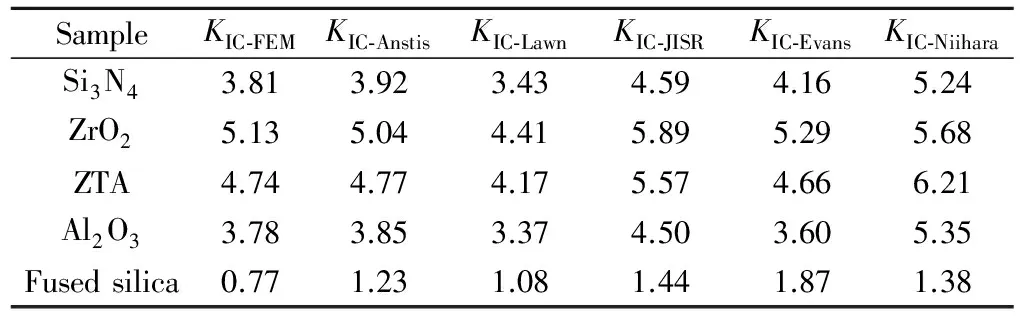
4 结论

