抛物线内接直角三角形一个性质的研究及其应用

☉湖北省武汉第三寄宿中学桂文通 袁俊峰

抛物线内接直角三角形一个性质的研究及其应用

☉湖北省武汉第三寄宿中学桂文通 袁俊峰

·武汉市桂文通名师工作室·

若一个三角形的三个顶点都在抛物线上，我们称这样的三角形为抛物线的内接三角形.本文就抛物线内接直角三角形的一个性质做一点研究和应用.

一、抛物线y=x2的内接直角三角形

命题1：如图1，已知直线AB交抛物线y=x2于A、B两点，若∠AOB=90°，则直线AB过定点.

这个命题的证明可以从三种不同的角度进行思考.

方法1：运用一元二次方程的根与系数的关系.

设点A（m，m2）、B（n，n2），直线AB的解析式为：y=kx+ b.

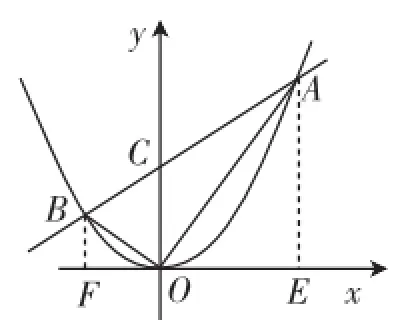
图1

联立y=kx+b和y=x2，

消元得x2-kx-b=0.

由根与系数的关系，得m+n=k，mn=-b.

作BF⊥x轴，垂足为F；作AE⊥x轴，垂足为E.

OC·（m-n）.化简得OC=-mn.

由方法1得mn=-1.

则OC=1为固定值.

故直线AB恒过其与y轴的交点C（0，1）.

由此可知：不论k为何值，直线AB恒过点（0，1）.方法2：运用面积法.

设点A（m，m2）、B（n，n2），直线AB与y轴的交点为C.作BF⊥x轴，垂足为F；作AE⊥x轴，垂足为E.

根据S△AOB=S梯形ABFE-S△AOE-S△BOF=S△AOC+S△BOC，可得

设点A（m，m2）、B（n，n2）.

OA2=m2+m4，OB2=n2+n4，AB2=（m-n）2+（m2-n2）2.

由OA2+OB2=AB2，得：（m2+m4）+（n2+n4）=（m-n）2+（m2-n2）2.化简得mn=-1.

从以上证明可知：若抛物线y=x2的内接直角三角形的顶点为（0，0），则斜边AB一定过定点（0，1）.

现在我们思考命题1的逆命题.

命题2：如图2，直线AB：y= kx+1交抛物线y=x2于A、B两点，抛物线上总存在一点D，使∠ADB=90°.

证明：设点A（m，m2）、B（n，n2）、D（t，t2），过点D作x轴的平行线EF，分别过点A、B作y轴的平行线，与EF交于点E、F.

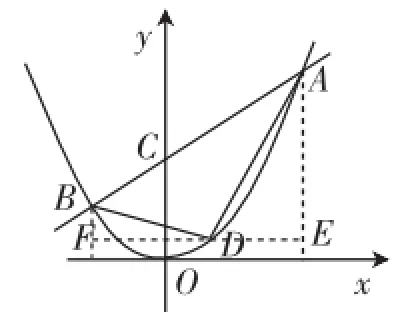
图2

则AE·BF=DF·DE.

即（m2-t2）（n2-t2）=（t-n）（m-t）.

化简得mn+（m+n）t+t2+1=0.

由命题1知m+n=k，mn=-1.

则kt+t2=0.

由点D的坐标与k无关，得t=0.即D（0，0）.

比较命题1、2，我们可以得到结论1.

结论1：对于抛物线y=x2的内接直角三角形，若斜边过定点（0，1），则直角顶点一定过定点（0，0）.反之亦然！

二、抛物线y=ax2的内接直角三角形

根据命题1、2的研究很容易得到结论2.

结论2：对于抛物线y=ax2的内接直角三角形，若斜边过定点，则直角顶点一定过定点（0，0）.反之亦然！

此时，我们自然思考如下两个问题.

（1）对于抛物线y=ax2的内接直角三角形，若直角顶点任意给定，那么它的斜边是否一定过定点？

（2）对于抛物线y=ax2的内接直角三角形，若斜边过一定点，那么直角顶点是否一定过一定点？

下面给出一般性探讨.

如图2，设直线AB过定点（p，q），则其解析式为y-q= k（x-p），与抛物线y=ax2联立，消元得ax2-kx+kp-q=0.

设点A（m，am2）、B（n，an2）、D（t，at2）.过点D作x轴的平行线，分别过点A、B作y轴的平行线，与直线EF交于点E、F.

化简得mn+（m+n）t+t2+

则（ap+at）k=-1+aq-a2t（※）.

（1）已知p、q，对于任意k，存在t，使（※）式成立，则（ap+at）k=0，且-1+aq-a2t2=0，解得t=-p，q=ap2

（2）已知t，对于任意k，存在p、q，使（※）式成立，则（ap+at）k=0，且-1+aq-a2t2=0，解得p=-t，q=at2+

结论3：对于抛物线y=ax2的内接直角三角形，斜边只有经过定点直角顶点才一定过定点（-p， ap2）.

结论4：对于抛物线y=ax2的内接直角三角形，若直角顶点任意给定（t，at2），则它的斜边一定过定点

对于抛物线y=ax2+bx+c的内接直角三角形问题，只需借助抛物线的平移，转化为抛物线y=ax2的内接直角三角形问题即可解决.

三、性质的应用

根据上面的结论，我们很易解决几道中考试题.

应用1：（2011年株洲市中考）孔明是一个喜欢探究钻研的同学，他在研究抛物线的性质时，如图3，将一把直角三角板的直角顶点置于平面直角坐标系的原点O，两直角边与该抛物线交于A、B两点，孔明将三角板绕点O旋转任意角度时惊奇地发现，交点A、B的连线段总经过一个固定的点，试说明理由并求出该点的坐标.

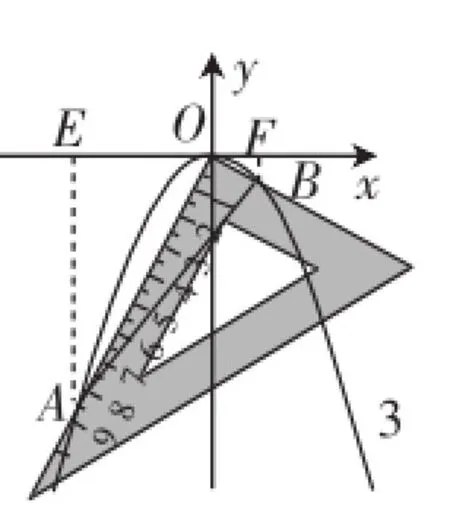
图3

运用结论3，易知AB过定点（0，-2）.

应用2：（2013年武汉市中考）如图4，点P是直线l：y=-2x-2上的点，过点P的另一条直线m交抛物线y=x2于A、B两点.

（1）和（2）略；

（3）设直线l交y轴于点C，若△AOB的外心在边AB上，且∠BPC=∠OCP，求点P的坐标.

分析与解：△AOB的外心在边AB上，即∠AOB=90°，由结论1知D（0，1），再根据∠BPC=∠OCP，得到CD=PD，可求得点P

应用3：（2014年武汉市中考）如图5，已知直线AB： y=kx+2k+4与抛物线交于A、B两点.

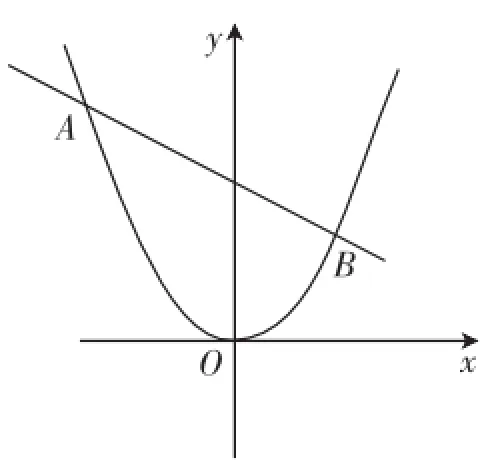
图5

图4

（1）直线AB总经过一个定点C，请直接写出点C的坐标；

（2）在抛物线上总存在点D，使∠ADB=90°，求点D到直线AB的最大距离.

（2）根据结论2，可得D点的坐标为（-2，2）.当CD⊥ AB时，点D到直线AB的距离最大，为

分析与解：直接运用结论4，可得点D（2，5）.

1.何银峰.代数方法解几何，数学问题不难做［J］.中学数学（下），2013（12）.

2.王兴富.立足学情教情追求正确导向——一道中考压轴题的命制历程及感悟［J］.中学数学（下），2014（12）.Z