新概念新情境新创意
☉江苏省如东县茗海中学 陈曙光
新概念新情境新创意
☉江苏省如东县茗海中学 陈曙光
为了给不同的学生提供公平的竞争环境,为了检测学生的发展潜能,一类““提供新材料、创设新情景、提出新问题”的题目应运而生,年年都有新面孔,年年都有新创意.它们立意考查学生的阅读、接受、分析、仿练、归纳、内化及应变等综合能力,在解决它们的过程中又可产生许多新方法、新观念,增强了学生的创新意识.此类试题新颖别致,夺人耳目.本文以2015年有关“代数”的考题为例,窥探其发展走势,用以指导教学.
一、定义一种新“数”
“数”是数学的重要成员,形式多姿多彩,都有自己的个性,蕴藏着许多奇妙的性质,在我们了解的数之外,设置相对陌生的一种“数”,需要我们现学现用,重在考查基本的数学素养.
例1(2015年重庆市A)如果把一个自然数各数位上的数字从最高位到个位依次排出一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数叫做“和谐数”.例如:自然数64746从最高位到个位排出的一串数字是:6、4、7、4、6,从个位到最高位排出的一串数字也是:6、4、7、4、6,所64746是“和谐数”.再如:33、181、212、4664、…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”,猜想任意一个四位“和谐数”能否被11整除,并说明理由;
(2)已知一个能被11整除的三位“和谐数”,设个位上的数字为x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的函数关系式.
解:(1)四位“和谐数”:1111、2222、3443、1221等.
任意一个四位“和谐数”都能被11整数,理由如下.
设四位“和谐数”是abcd,则:个位到最高位的排列为d、c、b、a,最高位到个位的排列为a、b、c、d.
由题意知两组数据相同,则a=d,b=c.
(2)设能被11整除的三位“和谐数”为zyx,则:个位到最高位的排列为x、y、z,最高位到个位的排列为z、y、x.
由题意知两组数据相同,则x=z.
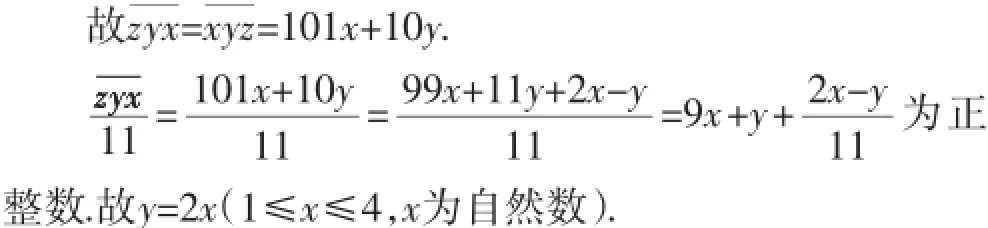
评析:本题首先给出了“和谐数”的内涵,接着用例子将抽象的概念具体化,然后从正、反两个反面考查和谐数概念的应用,还关注了试验、分析、判断及自学能力.
二、定义一种新“式”
从“数”到“式”是一种飞跃,形式同样多姿多彩,并超越于数具有了一般性的特征,蕴藏着更多奇妙的性质.若在我们已经认识的式之外,设置相对陌生的一种“式”,把学生认识的式的现实融入(负载新的内涵),使得考查更具现实性和挑战性,有助于创新意识的涵育.
例2(2015年自贡市)观察下表.
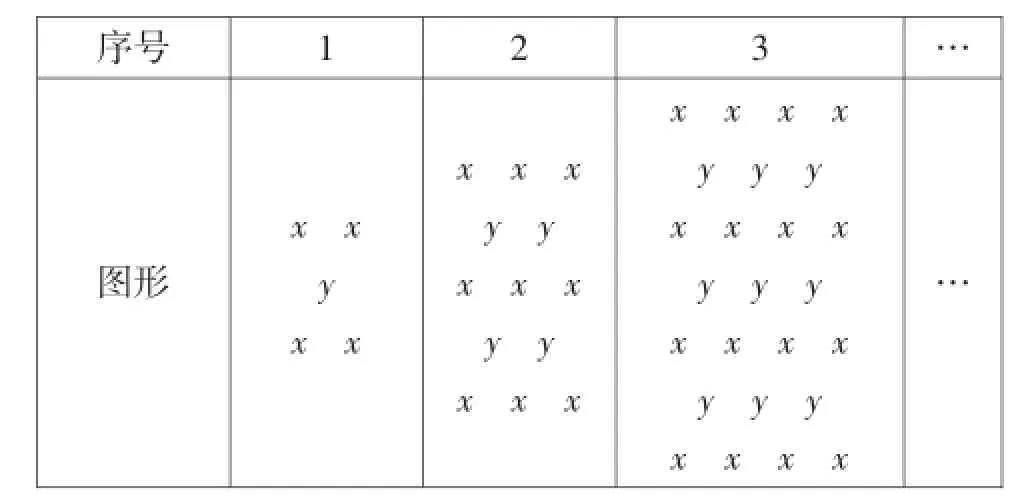
序号1 2 3…图形x x y x x x x x y y x x x y y x x x x x x x y y y x x x x y y y x x x x y y y x x x x…
我们把某格中字母和所得的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题.
(1)第3格的“特征多项式”为______,第4格的“特征

- 中学数学杂志的其它文章
- 别让“小智慧”从指间溜走*
- 抛物线内接直角三角形一个性质的研究及其应用

