别让“小智慧”从指间溜走*

☉湖南省常德市芷兰实验学校初中部 陈金红 罗先文☉湖南省常德市安乡县芦林铺中学 郭作华

别让“小智慧”从指间溜走*

☉湖南省常德市芷兰实验学校初中部 陈金红 罗先文
☉湖南省常德市安乡县芦林铺中学 郭作华

借用“勿以善小而不为”、“不扫小屋何以扫天下”、“不积小溪何以成江河”等名言，取其中的“小”，在数学中即小题目、小方法、小念头、小归纳等均是基本经验“小智慧”量的积累，虽算不上“高大上”，但却是解决大问题必须夯实的基本之策！看几个例子

例1有如图1和图2所示的两种广告牌，其中图1是由两个等腰直角三角形构成的，图2是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种大小关系用含字母a、b的不等式表示为_________．b2）、S2=ab，再比较大小；思路一：比差法，

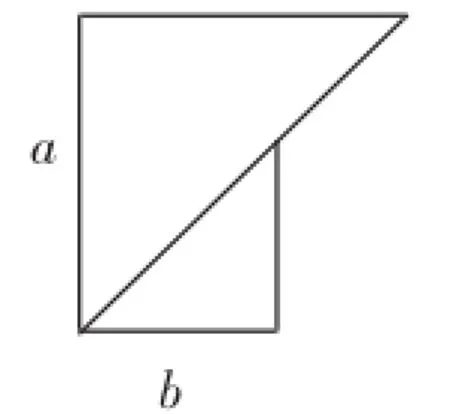
图1

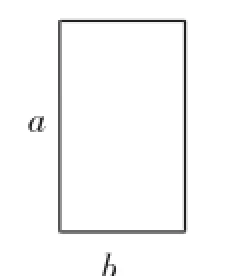
图2

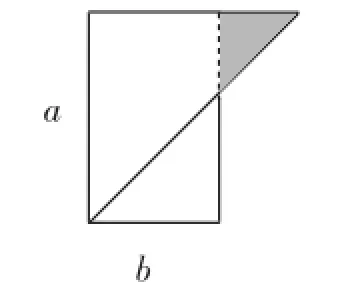
图3

若把此题简单地作为一个面积比较知识题，则其内在的教学价值黯然失色；不妨延伸设计：当边长a或b如何变化时，一般代数结论？此乃均值不等式的基本雏形的“亮相”！再可出示应用拓展作为向高中数学靠拢的压轴题型！

（1）猜想并写出第n个等式；

（2）证明你写出的等式的正确性

沿用从左证到右，但又要改进之亦可如何？观察不可少！从要证的等式发现，右边保留了左边第二个因式于是可以把左边第一个因式n改写为［（n+1）-1］，即左边=［（n+1）-1］n（运用乘法对加法的分配律）=右边，显然所用的基本知识，少之又少，可谓一个“小动作”带来何等兴奋的“智慧”之举！有想法即有“灵感”，再平常也不放过！

例3（七年级下册教材第157页第六章习题8）已知x1、x2、x3、x4、x5的平均数是x，方差是s2，a是任一常数.

（1）求x1+a、x2+a、x3+a、x4+a、x5+a的平均数与方差；

（2）求ax1、ax2、ax3、ax4、ax5的平均数与方差.

教学点评：关于数据组同加、同乘一个数后与原数据组的平均数、方差间的关系，运用定义不难推出：（1）平均数是x+a、方差仍是s2；（2）平均数是ax、方差变为a2s2！接着老师们一定会举出具体例子来巩固强化或一般推广！但常常是常规的变形，如“已知x1、x2、x3、x4、x5的平均数是5，方差是1，求x1+3、x2+3、x3+3、x4+3、x5+3的平均数与方差”.亦可不规则变形，比如“已知x1、x2、x3、x4、x5的平均数是5，求x1+1、x2+2、x3+3、x4+4、x5+5的平均数”.一般思维品质的做法：运用平均数公式去算的，以为不能运用上面的公式！优秀思维品质的做法：数据组可以规则化，具体即原数据组后面加的数1、2、3、4、5的平均数是3，故可看作求x1+3、x2+3、x3+3、x4+3、x5+3的平均数，于是利用上面的规律结论，它的平均数是5+3=8，于是x1+1、x2+2、x3+3、x4+4、x5+5的平均数为8.但是求方差却不可以如上使用！从而从根本上认识此方法的通性与局限性！

总之，如果不这样处理，那本习题的教学价值就没有从根本上挖掘与充分利用！学生可能的失误就会就此埋下了种子！对比，由“规则→不规则→规则”小技巧的习题变式使用，不可小视，也是一个“小智慧”呢！

例4（2012年泰安中考题）如图4，在△ABC中，∠ABC=45°，CD⊥AB、BE⊥AC，垂足分别为D、E，F为BC的中点，BE与DF、DC分别交于点G、H，∠ABE=∠CBE.

（1）线段BH与AC相等吗？若相等，请给予证明；若不相等，请说明理由.

（2）求证BG2-GE2=EA2.

教学点评：有位老师直接就用原题，貌似讲得有力，听得有味，学得充实，但是其后让学生单独再练习，结果令人大失所望！学生的真实想法：条件是依据但是谁的依据，又如何有效利用，不知如何下手？我的做法顺序呈现为：①如图5，在△ABC中，H为垂心，BH=AC，求∠ABC的度数（设计意图：考查垂心的定义、图示及辅助线、三角形全等的判定、等腰直角三角形的性质等）；②如图5，在△ABC中，H为垂心，∠ABC=45°，求证BH= AC（设计意图：知识点同上，方法点即认识逆命题造题法）；③在②的基础上，再添加条件F是BC的中点，连接DF交BE于点G，如图6，求证BG2-GE2=CE2（设计意图：除以上知识点外还考查了等腰三角形“三线合一”定理、勾股定理等）；④在③的基础上，再添加条件∠ABE=∠CBE，求证BG2-GE2=EA2.（设计意图：除以上考点外，继续分散目标对象，加大难度，考查转化思想方法；还考查：可运用平方差公式改证（BG+GE）（BG-GE）=AE2，也即证BE×（BG-GE）=AE2，呈现射影定理模型，于是可通过延长BE到点O，使BG=GO，于是即证BE×OE=AE2，显然由FG为△BCO的中位线、DF⊥BC，可得∠BCO=90°，即有Rt△BCO中CE是斜边BO上的高，运用射影定理立马可得要证的结论！让代数、几何的融合，知识的拓展、模型的挖掘、辅助线的合理运用有了现实平台）

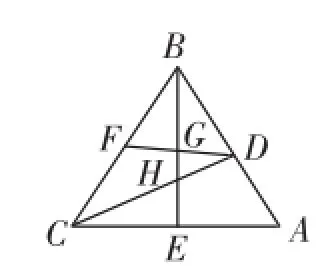
图4

图5

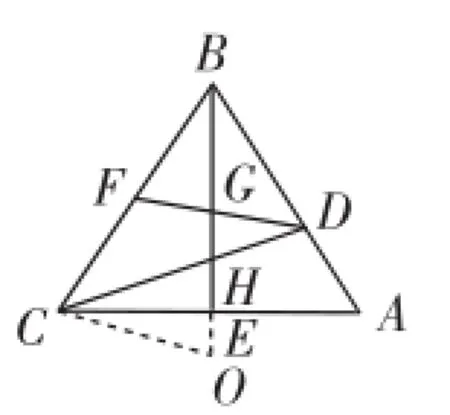
图6

先改编为一系列的小题目，让学生作为铺垫题自我练习，再交流讨论条件在问题中的地位和作用，课堂表现，兴趣浓、积极性高、各个层次的学生都学有所获；接下来的环节：综合这些小题目，即出示原题即2012年泰安中考题，由于有上面对条件的一些基本认识和经验积累，很快大部分的同学得出了完整解法，并感叹综合题实质是一系列小题目的“混合体”，其他同学也或多或少的有些思路和步骤，只要时间再宽裕点，也能写出个一二三！效果大不一样！关于几何推理能力的培养是一个常谈常新的教学课题，看来“给点时间，常下位（试验、合作、取样）看看”，不难得到都知晓但不一定常用的举措：先分解为“基本典型的小题目系列”，再综合这些小题目，让条件混杂在一起，不再有针对性，从而使条件被集中、被选择的空间增大，自然加大了坡度，其实施源于对小题目细致分析布局所致，让学生深深体会出“由小变大、由大变小，拆与拼”，实乃组合与分解的有机融合过程而已，有效解题的关键是弄明白条件在目标中的作用、地位和价值！

无需再例，静下来的习惯、突破常规的意识、挑战已有经验和定势、不断创新与时俱进的信念、有机整合串联的方法巩固行动，对平常不放过、小处着眼等，这些好的方式方法是来自于平时“小智慧”的不断积累与创造使用后升华的结晶，由此我们呼吁：别让“小智慧”从我们指间溜走！

1.义务教育课程标准实验教科书·数学（初中）［M］.长沙：湖南教育出版社，2014.

2.陈金红.“典例导题·问题驱动”案例片段［J］.中学数学（下），2013（1）.

3．陈金红.在“自然拓展”中拔高案例解读［J］.中学数学（下），2013（4）.

4.陈金红.你真的看过教材吗？［J］.中小学数学（初中），2015（1-2）.

5．陈金红，郭作华.常见，但有时不可视而不见［J］.教育科学论坛，2015（8）.H

全国教育科学“十二五”规划2013年度教育部规划课题FHB130512《生命课堂视野下的教学案例研究》阶段性成果之一.