抛物线准线、焦点考题的教学导向之思——从2015年江苏宿迁中考第26题说起

☉江苏省海门市东洲国际学校 许玉萍

抛物线准线、焦点考题的教学导向之思
——从2015年江苏宿迁中考第26题说起

☉江苏省海门市东洲国际学校 许玉萍

自从2010年江苏某市在中考最后一题引入抛物线的准线、焦点问题结构以来，每年全国各地都有一些地区在最后一道题上设计与之结构相近的把关题.对于这类考题，如果复习备考期间有意识地准备的话，考生在考场上将获得居高临下的结构洞察，从而与那些没有补充过类似性质的考生造成解题效率上的差距，这也是另一种意义上的不公平现象.本文从2015年江苏宿迁中考把关题说起，列举另外两道相关的中考题，最后就这类考题的教学导向做一些反思，供研讨.

一、从一道中考题的求解说起

考题1：（2015年江苏宿迁中考卷，第26题）如图1，在平面直角坐标系中，正方形ABCD和正方形DEFG的边长分别为2a和2b，点A、D、G在y轴上，坐标原点O为AD的中点，抛物线y=mx2过C、F两点，连接FD并延长交抛物线于点M.

（1）若a=1，求m和b的值；

（3）判断以FM为直径的圆与AB所在直线的位置关系，并说明理由.

图1

思路简述：（1）由a=1，根据正方形的性质及已知条件得出C（2，1）.将C点的坐标代入y=mx2，求出m=，则抛物线的解析式为.再将点F（2b，2b+1）代入y=即可求出

（2）由正方形ABCD的边长为2a，坐标原点O为AD的中点，得出C（2a，a）.将C点的坐标代入y=mx2，求出m=则抛物线的解析式为再将点F的坐标（2b， 2b+a）代入y=整理得b2-2ab-a2=0.把a看作常数，利用求根公式得出b=a（负值舍去），那么

（3）先利用待定系数法求出直线FD的解析式为y=x+ a.将y=x+a代入值舍去），则M点的坐标为（又点F，利用中点坐标公式得到以FM为直径的圆的圆心O′的坐标为（2a，3a）.再求出O′到直线AB（y=-a）的距离d=3a-（-a）=4a，则以FM为直径的圆的半径为：

“结构”反思：现在我们来反思第三问的深层结构.首先把高中数学中提及的抛物线的准线、焦点的相关定义简述如下：平面内与一个定点F和一条直线l的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点，直线l叫做抛物线的准线.比如抛物线y=ax2+bx+c的焦点为.不妨验证一下，“考题1”中，点D（0，a）是抛物线y=mx2的焦点吧！它的准线为y=-a，即直线AB.于是，“考题1”的深层结构如图2所示.

图2

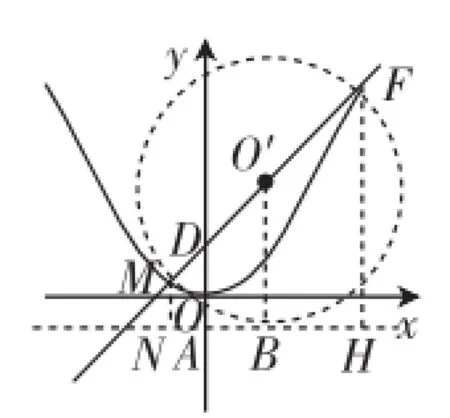
图3

在图2中，以MF为直径的圆O′与直线AB相切于B点，点O′、C、B在同一直线上；再把无关线段排除、删减得出图3，过M、F、O′分别向直线AB作垂线段MN、FH、O′B，由上面提及的准线、焦点的性质，易知MN=MD，FH=FD，而梯形MNHF中，O′B是中位线，所以以MF为直径的圆O′与直线AB相切也就是在这个“结构”之下的必然.

二、抛物线的准线、焦点相关考题列举

考题2：（2015年四川资阳，第24题）已知直线y=kx+b（k≠0）过点F（0，1），与抛物线相交于B、C两点.

（1）、（2）略.（限于篇幅，与本文无多大关联，略去不引）

（3）如图4，设B（m，n）（m<0），过点E（0，-1）的直线l∥x轴，BR⊥l于R，CS⊥l于S，连接FR、FS.试判断△RFS的形状，并说明理由.

图4

图5

因为点B在抛物线上，所以m2=4n.在Rt△BTF中，BF=∠BFC=90°，所以△RFS是直角三角形.

三、关于教学导向的思考

1.简单下放高中知识点的考查方式值得商榷

由于抛物线的准线、焦点的性质是高中学段的内容，所以在中考试卷中出现以此为结构的考题应视为“超标”考题.然而像上面提及的两道考题都属于“擦边球”类型，它们并没有直接考查相关知识点，然而如果备考师生补充过类似的知识，则对不同考生来说可能会造成一种不公平现象，他们在惜时如金的中考考场上耗时费力最后获得他人早就熟知的性质.顺便指出，像考题1中的思路突破时，如果熟悉“中点公式”也有助于快速突破思路，而这也是高中阶段的一个知识点.

2.解题教学中引入“准线、焦点”是可行的

虽然笔者对中考题中出现“准线、焦点”现象持批判态度，但这并不表示初中解题教学中就需要严守课标规定，恰恰相反，如著名特级教师李庾南老师所指出的“课标只是底线，需要人人达到的，面对课标，我们的态度是‘下要保底，上不封顶’”.这样看来，平时教学过程中，恰时恰点地引入所谓高中知识，让优秀学生能挑战更为广阔、深刻的数学性质，是非常值得尝试的，经常开展这样的教学，也可以让优秀学生避免大量“空转现象”.顺便提及，最新的人教版九年级教材在二次函数“数学活动”中就曾安排与抛物线相关的作图与探究活动，有效渗透了抛物线的准线、焦点的有关性质，值得关注.

四、结束语

中考命题使命光荣、责任在肩，首先不能出现科学性错误，又要确保应有区分度，利于选拔学生，同时还要兼顾考题所带来的教学导向，毕竟对于广大基层一线教师来说，本地区的考试是更为现实的教学引领.期待着中考卷在把关题的设置上精心构思，既体现课标精神，导向教学，又能反映数学追求简约、深刻的特征.

1.章建跃.发挥数学的内在力量，为学生谋取长期利益［J］.数学通报，2013（2）.

2.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

3.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

4.刘东升.经历问题生成，深刻理解教材——人教八上“每日一题”的命题实践与思考［J］.中学数学（下），2014（4）.Z