中考复习，如何培养学生的批判性思维——从两道中考模拟考试压轴题说起

☉广东省广州市玉岩中学 吴光潮

中考复习，如何培养学生的批判性思维
——从两道中考模拟考试压轴题说起

☉广东省广州市玉岩中学 吴光潮

中考数学试题，尤其是压轴题，不仅要求考生具有扎实的数学基础知识，还要求考生具有良好的思维品质.许多考生经历几轮中考复习，形成了唯师、唯书、唯权威的共同弱点，缺乏对知识信息、解题思路怀疑的勇气和筛选的能力，缺乏批判精神和创新意识，在一定程度上强化了思维定势的负效应，影响了创造性思维的发展.中考综合复习，必须重视培养学生的批判性思维.下面笔者从两道中考模拟考试压轴题说起，谈谈个人的一些认识，旨在和同行探讨交流.

一、试题再现

例1（2015年广州市萝岗区一模考试第22题）如图1，正方形AEFG的边长为1，正方形ABCD的边长为3，且点F在AD上.

（1）求S△DBF；

（2）把正方形AEFG绕点A按逆时针方向旋转45°得图2，求图2中的S△DBF；

（3）把正方形AEFG绕点A旋转一周，在旋转的过程中，S△DBF存在最大值与最小值，请直接写出最大值_______，最小值_______.

图2

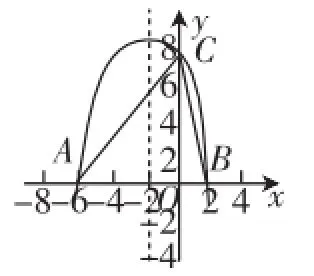
图3

例2 （2015年广州市萝岗区一模考试第23题）已知抛物线y=ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，OB=2，OC=8，抛物线的对称轴是直线x=-2.

（1）求此抛物线的表达式；

（2）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF//AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

（3）在（2）的基础上说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由.

二、解题思路及考生思路受阻成因分析

1.考生缺乏批判性思维中质疑的勇气和习惯

心理学家认为：“疑，最容易引起定向———探究反射.”学生解题不能“疑”，就没有了这种反射，思维就不会应运而生；没有更深层的“疑”，就不会有各种更开阔的解题思路，不会有各种奇妙的创新性解法.事实上，本题正是考生缺乏批判性思维中质疑的勇气和习惯，学生思维僵化、不会变通、不会质疑和筛选解题思路造成解题困境.

通常，任何问题基本上可以从正面直接进攻——直接法，也可以迂回进攻——间接法，正难则反.

求面积问题如果直接用面积公式受阻，是否还有其他间接的解法？

学生如果经过如上质疑、批判性思维，不难得到如下解法而顺利求解：

第（1）问，间接求解——割补法中的“切割法”——S△DBF=S△ADB-S△ABF.

第（2）问，间接求解——另解1（割补法中的“切割法”）：设BF与AD交于点M，则S△DBF=S△MDF+S△MDB=，而AM在△BFG中用相似即可求出.

另解2（“割补法”）：S△DBF=S梯形FGAD+S△ADB-S△FGB.

由上可知，教师在教学中要培养学生的这种探索性质疑、否定性质疑的精神.

2.考生缺乏独立批判性思维的时间和空间

学生在平时训练时不但要“疑”，还要“善疑”.培养批判性思维的前提是学生要有批判性思维独立的时间和空间.在平时训练中，如果学生缺少独立的时间和空间，其理性和独立思考能力就较差，这一状况就决定了他们难以追求对事物真相或本质的认识.

比如，例1第（2）问，直接公式法和间接分割法求面积是常规求法.还有没有其他解法？——另解3（面积转化法）：连接AF，由题意易知AF∥BD，所以

x+8.第（2）问，学生面临同例1第（2）问一样的思维受阻点.本问中面积S的求法：

利用相似性质，易知hF∶OC=BF∶BC=BE∶BA（AC//EF）.

从而hF∶8=（8-m）∶8，所以hF=8-m.

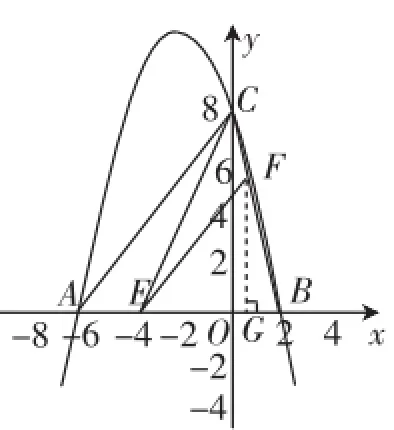
图4

由上可以看出，例1第（2）问的“另解3（面积转化法）”与例2第（2）的问“思路2（割补法转化）”是相对较优的解法.但学生受阻的根本原因在于“问题转化”包含较大的思维容量，对初中学生的创新思维、批判性思维要求较高，学生平时批判性思维训练的时间和空间如果得不到保障，他们难以追求对事物真相或本质的认识，思维质量远达不到考试要求.独立的时间和空间给学生带来的是思考、反省和改正不足的机会，让学生乐于自主学习、自觉实践，不断拓展思维视域、提升思维境界，批判性思维能力就越强；没有独立的思维就不可能具有探索精神，也不可能具有创新思维的发生和发展.

3.考生缺乏批判性思维中信息筛选的能力

批判性思维本质上就是打破传统固有的另一种思考，不仅进行探究性质疑，也可以是否定性质疑：否定就意味着需要自己重新再来，不迷信.所以更要培养学生信息筛选的能力，而考生缺乏批判性思维中的筛选能力，导致解题受阻.

实际上，上述过程就是“最值问题”中“建立目标函数，求函数最值”的常见思路.在初三复习中，“最值问题”是一类典型的综合问题，中考题经常考.平时训练，教师也反复给学生建立了“目标函数法”的基本思路和解题步骤.学生也基本熟悉这种套路.

但正是因为这种“常见的”、“熟悉的”思路，给考生在处理例1的第（3）问时，带进了误区：

例1的第（3）问，很多考生一看题目要求“S△DBF存在最大值与最小值”，立马陷入思维定势：“目标函数法”求最值.实际上，“目标函数法”求最值只是从代数角度思考的一种解法，那么从几何角度有没有求最值的方法？本题到底是该从几何角度还是代数角度去思考？

考生需要有批判性思维，更要有良好的信息筛选能力.当考生如果尝试从代数的角度用目标函数求解时，会发现本题要想建立S△DBF的目标函数，是十分困难的事情：因为本题随着正方形AEFG的旋转，S△DBF如果用直接公式法，除了DB不变外，其余的边及其对应的高都在变，而且不易用代数式表示（即使是表示DB边上的高，也不易），如图5；如果用割补法，同样面临很大阻力.

良好的筛选能力，会帮助我们敏锐地感觉：打破思维定势，用几何法去思考将迎刃而解.

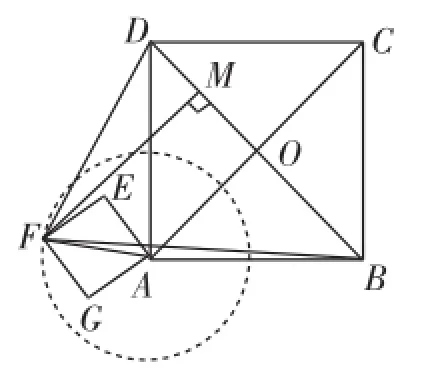
图6

由此看来，很多时候，我们的思维受阻，不一定是知识不到位，而是我们思考的角度不对，这就要求我们思维要有较强的灵活性.批判性思维的培养显得尤为重要.

三、几点感悟——如何培养学生的批判性思维

1.教师要注意总结开展批判性思维的教学途径和教学方法

教师在备课时，要经常“下水”动手做题，多反思，充分估计学生会犯的错误及其思维受阻的节点，反思应该如何进一步挖掘在教学时给学生批判性思维训练的教学机会.教师寻找批判性思维的教学方法，为学生提供发现数学问题、思考数学问题的机会，引出学生的不同观点，并使之理解.

教师要在数学概念教学中、在例题和习题的教学中等积极开展批判性思维的教学，并且将批判性思维贯穿整个数学课教学活动始终.教学时，通过探究学习培养学生的批判性思维；通过多种活动，如利用错解辨析开展批判性教学，通过辨析求异等培养学生的批判性思维.

2.教师教学时，要培养学生独立批判性思维的时间和空间

独立的时间和空间是培养批判性思维的前提.我们教师在中考综合复习时，既要落实好常规题型的“通性通法”的教学，让学生初步形成各种题型模式化的解题策略，重视发挥定势思维的积极作用；又要积极引导学生开展独立批判性思维的训练，提供足够的时空，使学生形成批判性思维的习惯，促进创新性思维的发展，同时注意利用批判性思维打破思维定式，防止思维定势的负面影响，让思维更具有灵活性.

3.教师教学时，要培养学生批判性思维的质疑精神和筛选能力

教师讲题教学，要注意引导学生从常规思路与非常规思路、正向与逆向、直接与间接、代数角度与几何角度等去思考问题，鼓励探究性质疑和否定性质疑.注意一题多解、多题一解，多反思，多比较，多筛选，优化解题思路，优化解题思维，提升创新性思维.

总之，要提升学生的思维品质，提升学生思维的广阔性、深刻性、灵活性和创新性，培养学生的批判性思维就显得十分重要.教师要注意教法，积极开展对学生批判性思维的培养，并且贯穿整个教学过程.

1.管宏斌.论批判性思维在数学教学中的建构［J］.教学与管理，2006（1）.

2.马灿宏.培养学生的创新思维［J］.中学数学（下），2005（1）.H