一种无乘法器的DLMS导航抗干扰算法设计
黄 超,李朝海
(电子科技大学 电子工程学院,四川 成都611731)
0 引言
卫星导航系统是最近半个世纪发展起来的通过卫星作为通信平台的无线电通信导航系统,该系统能提供全天候连续高精度的位置、速度和精密时间信息[1],现在已成为军事大国在战争中获得军事优势的重要手段之一,所以具备抗干扰能力、能够抵抗来自不同敌对力量的各种干扰的导航接收机在未来的军事应用中具有重要的意义。
1 抗干扰方案
目前,在导航系统中应用比较多的是空域自适应算法和空时联合自适应算法。空域自适应算法实现简单,耗资源少,但由于其只能在空域上进行滤波,所以对于宽带干扰的抑制能力有限,容易形成零陷点扩散和偏移;而空时联合自适应算法可以利用每个天线阵元后面的延时抽头来增加自适应算法的频率响应,从而提高算法对宽带干扰的抗干扰能力。空时自适应算法的结构如图 1所示[2]。
本文采用功率倒置算法来实现自适应抗干扰,该算法是基于线性约束最小方差(LCMV)准则的,算法使自适应阵列的输出功率最小[3]。对于导航信号和干扰,功率倒置算法均对其进行抑制,输入阵列信号能量越大,算法零陷深度就越深,由于干扰信号通常情况下为压制式干扰,其能量远远大于负信噪比的导航信号。所以功率倒置算法适合卫星导航抗干扰。图2为空时二维功率倒置算法结构框图。

图1 空时自适应算法结构框图
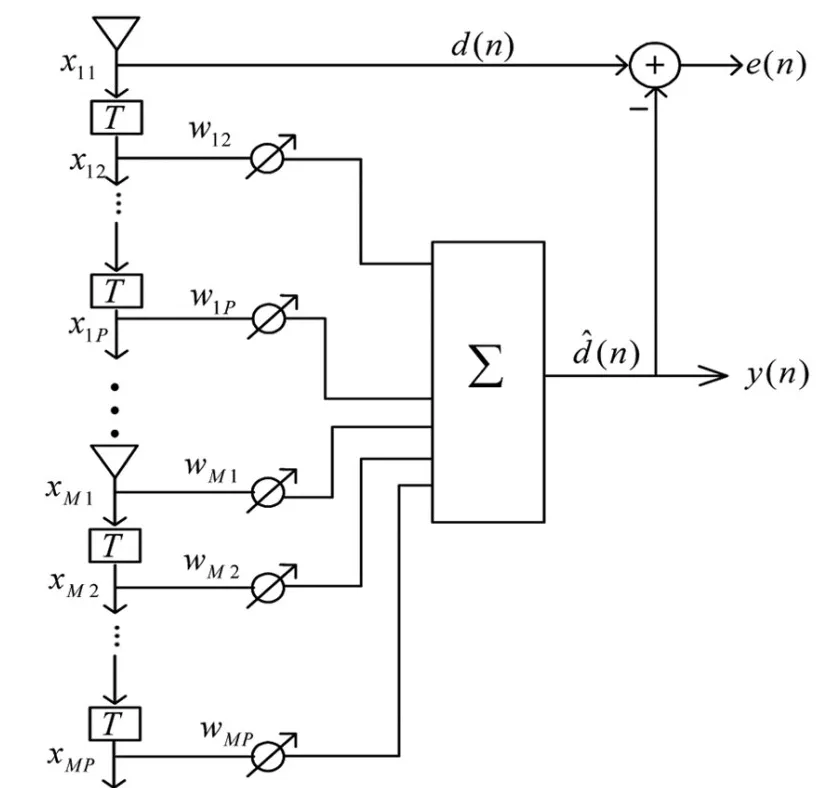
图2 空时二维功率倒置算法结构框图
将LMS算法应用于功率倒置算法,即将第一路天线接收到的信号作为参考信号,其他支路信号通过LMS算法加权求和逼近第一路天线信号,相减输出,从而使得输出信号功率尽量小。
2 一种无乘法器的DLMS算法设计
在实际工程中对LMS算法进行硬件实现,如FPGA实现等,受限于硬件处理速度,无法在较高的采样率的一个快拍中完成迭代运算,需要引入DLMS(延时最小均方)算法[4]。DLMS算法是在权值更新和误差计算中的乘法和加减法运算中引入延时单元D,当前DLMS算法的权值更新是用经过延时D以后的误差信号和输入信号来完成的,加入延时信息后的DLMS算法公式如下。
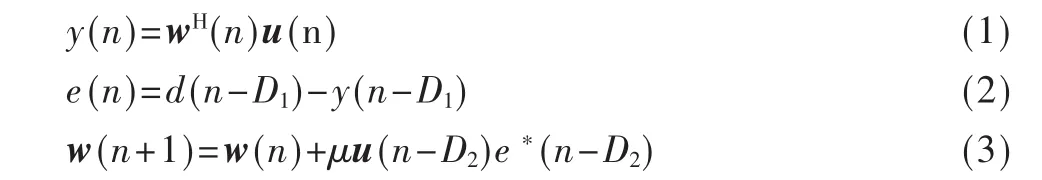
当延迟小于系统阶数时,误差梯度:

此时延迟后的数据不降低收敛速度。由于采用空时二维自适应算法,所以系统阶数较空域自适应算法大,更适用于流水线设计。
在FPGA中,乘法器资源非常宝贵,一般较为昂贵的FPGA中才有较多的乘法器核。设计使用CORDIC算法实现乘法运算,不过其缺点是如果要得到较高的运算精度,则运算需要多级,会引入较大的延迟。若是将其使用在空域DLMS算法中,并要求较高的计算精度,则带来的延迟会引起梯度估计的较大误差,同时还会影响收敛速度;空时二维自适应算法具有较大的系统阶数,所以CORDIC算法引入的延迟不会对梯度估计造成较大的误差,同时对DLMS算法的收敛速度也没有影响。所以本设计使用CORDIC算法来实现DLMS算法中的乘法运算,并结合设计要求对相关参数设计进行了介绍。
2.1 基于CORDIC算法的乘法器设计
CORDIC(Coordinate Rotation Digital Computer)算法具有圆周和向量两种模式,在两种模式下能够计算正弦余弦、反正切、平方根、双曲余弦正弦、乘除法等运算[5]。在CORDIC算法的圆周模式下能够完成乘法运算,其迭代方程如式(5)~式(7)所示。

但是传统的CORDIC乘法运算只有满足|z0|<2的情况下,计算结果才是正确的,表1为CORDIC算法的MATLAB仿真结果,可以看出确实|z0|>2时计算结果错误。

表1 传统CORDIC乘法运算结果
考虑到FPGA中的运算都是整数的运算,所以对传统 CORDIC乘法运算进行修改,将式(5)、式(6)中的 2-i改为2i,并且迭代以变量i的降序来进行。假设系统的AD采样位数为16位,所以为保证乘法运算精度,设计16级CORDIC迭代,即是变量i从16开始降序迭代。修改后的CORDIC运算迭代结构示意图如图3所示。运算的最终输出为result=y0+x0z0。表 2为修改后的 CORDIC乘法运算的结果。从表2中可以看出,在16位位宽下修改后的CORDIC算法能保证整数运算的正确。
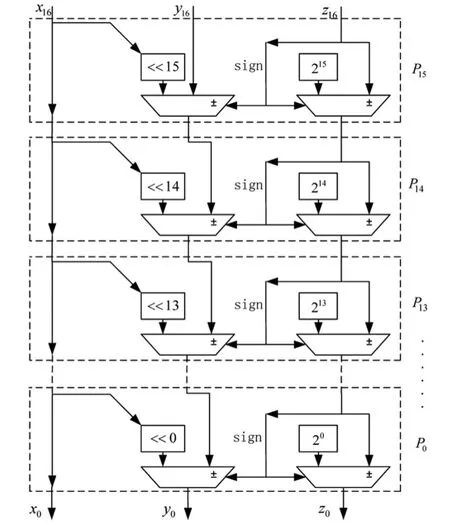
图3 修改后的CORDIC运算结构示意图

表2 修改后的CORDIC乘法运算结果
CORDIC算法容易实现流水线设计,在每一级迭代之间(P15、P14、P13……)均可引入流水线,从而提高设计的速度。本设计使用CORDIC乘法单元代替DLMS算法中的乘法运算,并在CORDIC乘法单元中引入适当的流水寄存器,从而提高CORDIC乘法单元的运行速度。
2.2 空时二维DLMS算法的时域抽头数设计
空时二维DLMS算法的参数设计关键在于确定天线阵列后的抽头数。抽头数决定了空时二维自适应算法的阶数,同时决定了算法中能引入流水线的上限和对宽带干扰的抗干扰能力。分析干扰信号被抑制的程度,采用求解未抗干扰前干扰信号+噪声的功率和抗干扰后干扰信号+噪声功率的比值作为标准。用式(8)表示,INR称为干扰抑制比:

使用宽带干扰建模进行仿真,得到干扰抑制比结果如表3所示。从表3中可以看出,延迟抽头数P增加会使DLMS算法的干扰抑制比增加,不过同时会增加自相关矩阵R的条件数,使R病态,导致DLMS算法收敛性能降低。当P过大时反而会降低干扰抑制比,同时会增加硬件实现的资源消耗。所以系统综合选取抽头数P=5。

表3 实测宽带数据的延迟抽头数性能分析
2.3 空时二维DLMS算法的simulink实现
本文采用Simulink完成算法设计的仿真,图4为使用CORDIC乘法单元实现的复数乘法器,其中CORDIC乘法单元的结构如图3所示。复数乘法器的表达式为:
x+yj=(a+bj)(c+dj)=(ac-bd)+(ad+bc)j (9)
设计使用CORDIC乘法单元完成式(9)中的4个乘法运算,再结合一次加法运算和一次减法运算从而完成复数乘法器。CORDIC乘法单元中具有16级迭代单元,设计插入流水线以增加硬件的运算速度。由于抽头数选择为5,则系统阶数为5×4-1=19,考虑不影响梯度的估计,这里设计在16级迭代单元中插入8级流水,使得梯度估计延迟数为11个延迟单位,小于系统阶数,不会影响DLMS算法的收敛性能。图5为四天线、抽头数为5、步长取μ=2-4的DLMS抗干扰算法的第一路天线后端的4路抽头的迭代模块的结构示意图。

图4 使用CORDIC乘法单元实现的复数乘法器
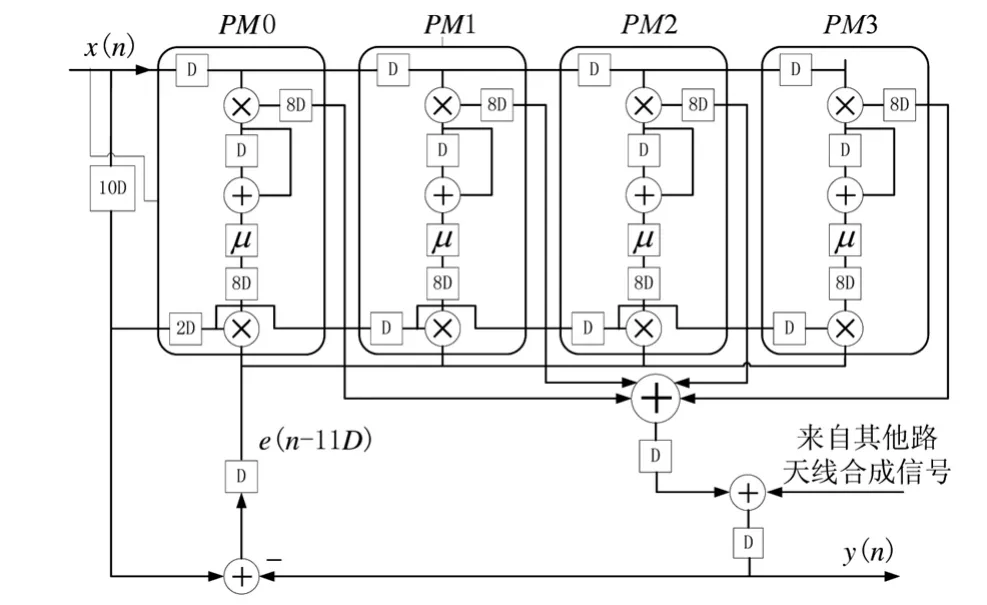
图5 第一路天线后4个抽头信号迭代运算Simulink建模图
设计中需要考虑的一个问题是要保证流水线后的数据同步地进行处理。设计中CORDIC乘法器引入了8个单位的延迟,再加上4路天线后时域抽头输出的yi(n)(i=1,2,3,…,19)相加过程中引入两级加法树延迟,所以y(n)的延迟是10个单位的延迟,需要将参考信号d(n)也延迟10个单位后保持与y(n)的同步,同时参考信号 d(n)与 y(n)相减的减法器后再加入一级延迟,使得e(n)的延迟数为11个单位,所以需要将输入信号u(n)延迟11个单位后与e(n)相乘得到梯度估计,如图5所示。
3 测试结果及分析
利用Simulink对实测采集数据进行算法的仿真,其中采集数据的参数为4路天线数据,中频信号频率为46.52 MHz,带宽为 20.46 MHz,采样率为 65.28 MHz。实验中给系统添加了一个50 dB干信比的1 268.52 MHz的单频干扰信号和一个65 dB干信比的宽带QPSK信号,信号中心频率为1 268.52 MHz,带宽为 20 MHz,其信号频谱如图6所示。仿真输出结果如图7和图8所示。其中图7为基于CORDIC算法的DLMS抗干扰算法的输出信号e(n)的频谱,从结果中可以看出,在数字中频18.76±10.23 MHz频段,e(n)输出的频率分量与输入信号频谱相比较,加入的单频和宽带干扰被有效地抑制了,带内功率谱密度降低为-80 dBm/Hz,提高了输出的信干噪比。图8为普通DLMS算法与基于CORDIC算法的DLMS算法的权向量ω11的收敛曲线的比较。从结果中可以看到,基于CORDIC算法的DLMS算法没有影响算法的收敛性能以及最终的最佳权向量。

图6 输入DLMS算法的干扰加信号频谱图
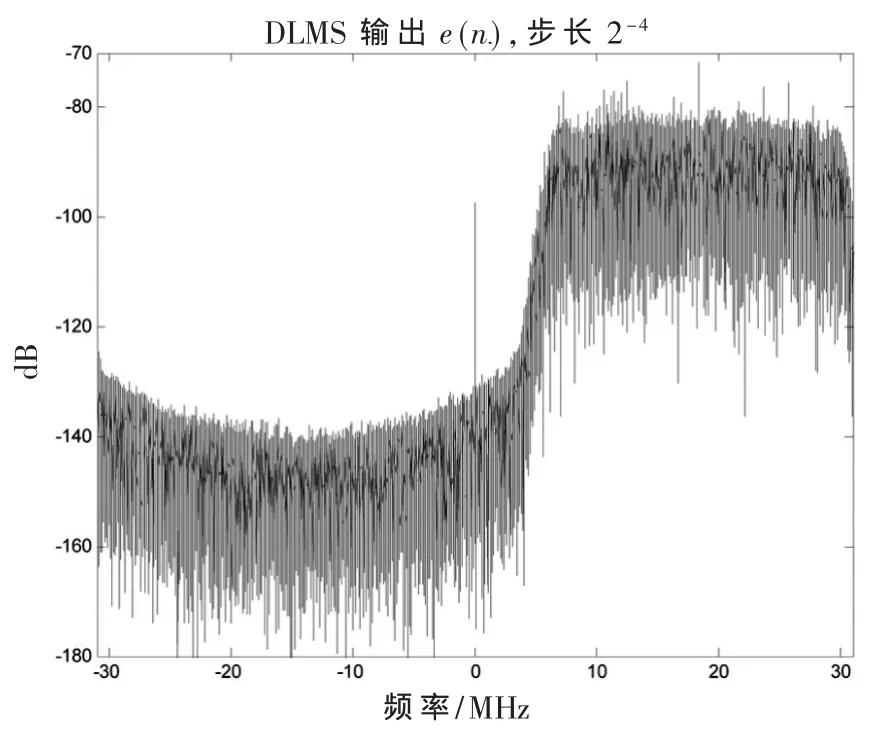
图7 基于CORDIC算法的DLMS抗干扰算法的输出信号的频谱
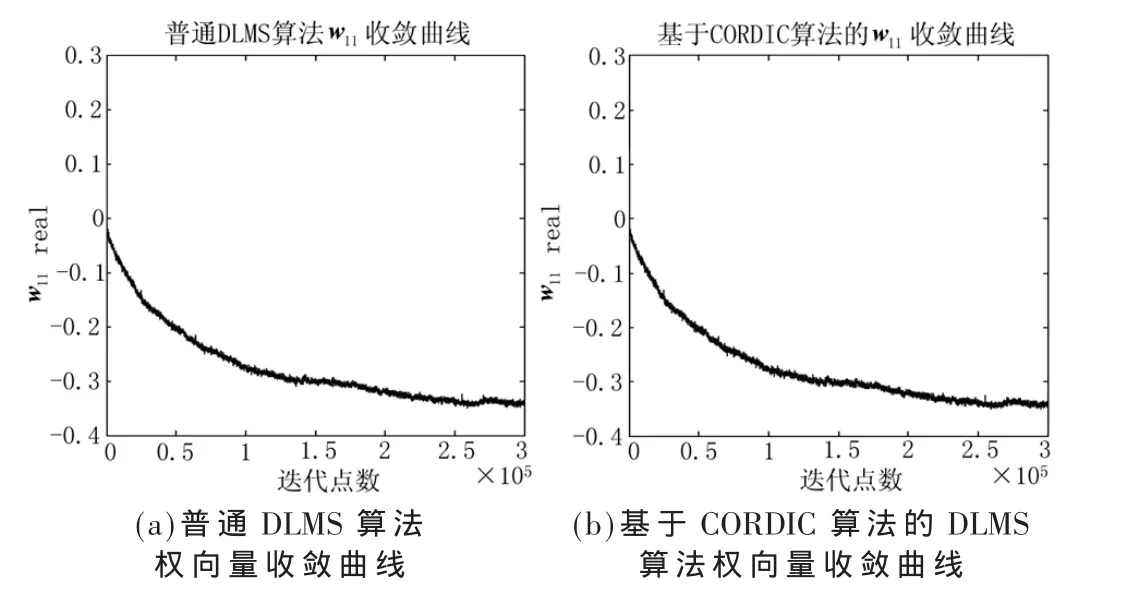
图8 普通DLMS算法和基于CORDIC算法的DLMS算法的权向量收敛曲线
4 结束语
本文研究了一种基于CORDIC算法的无乘法器的DLMS抗干扰算法设计,结合实测数据仿真,分析了算法中关键参数的选取,重点阐述了在Simulink环境下,基于CORDIC算法的乘法器及相关的DLMS算法的结构与实现。最后完成了对算法的仿真及验证,从仿真结果可以看出本算法设计不影响DLMS算法的特性,同时节约了乘法器资源,在CORDIC算法中引入流水线,能有效地提高算法的速度。
[1]童铠.中国导航定位卫星系统的进展[J].中国航天,2002(8):3-10.
[2]郭艺.GPS接收机空时抗干扰理论与实现关键技术研究[D].长沙:国防科学技术大学,2007.
[3]龚耀寰.自适应滤波[M].第2版,北京:电子工业出版社,2003.
[4]Lok-Kee Ting,Roger Woods.Virtex FPGA implementation of a pipelined adaptive LMS predictor for electronic support measures receivers[J].IEEE Transactions on Verylarge Scale Integration(VLSI)Systems,2005(1).
[5]MEHER P K,VALLS J,Tso-Bing Juang,et al.50 years of CORDIC:algorithms,architectures,and applications[J].IEEE Transactions on Circuits and Systems,2009,56(9).

