Phase2软件在隧洞开挖围岩支护时机中的应用

何 欣,曹怀园,刘永智,刘洁玉

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

文章编号：1006—2610(2015)03—0049—05

Phase2软件在隧洞开挖围岩支护时机中的应用

何 欣,曹怀园,刘永智,刘洁玉

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

新奥法支护理论允许围岩变形，“适时”支护，能够保证围岩稳定的前提下，减少支护措施。文章利用phase2软件，引入应力释放法和弹性模量折减法解决“适时”的问题，将新奥法理论应用于德尔西水电站工程引水隧洞支护结构设计中，采用量化、清晰易懂的方式证明了合理地选择支护时机可以优化支护结构、减少工程投资，对隧洞工程支护结构设计具有实际意义。

隧洞；支护时机；新奥法；位移；Phase2;德尔西水电站

0 前 言

地下洞室工程广泛地应用于水利水电工程中，其中围岩稳定问题是地下洞室最突出的工程问题。人们开始探索地下洞室的支护设计理论，早在19世纪初，学者认为只有衬砌作为受力结构，承受上部围岩荷载，衬砌厚度设计偏大。20世纪60年代，新奥法作为新兴的隧道设计方法得到关注，新奥法理论[1-2]是“合理”支护时机最初的理论基础，最佳支护时机的确定，使我们在确保围岩稳定和节约支护材料的工作中充满自信。然而如何确定支护时机成为工程中的难点。

在德尔西水电站引水隧洞围岩稳定计算中，我们应用了Phase2软件提供的2种确定支护时机的方法，并对比其与及时支护时3种不同情况下围岩变形和喷锚支护结构受力情况，为地下洞室开挖围岩稳定分析提供参考和建议。

1 支护时机确定的相关理论

1.1 “允许位移量”的确定

新奥法的基本观点：把岩体视为连续介质，根据岩体具有的黏性、弹性、塑性的物理性质，并利用洞室开挖后围岩应力重分布而产生的变形到松动破坏有一个时间效应的动态特点，“适时”地采用薄壁柔性支护结构(以锚喷为主要手段)，与围岩紧密贴合起来共同工作，从而调动并充分利用了天然围岩的自身承载能力，以达到洞室围岩稳定的目的。

目前，人们正在进行各种努力以寻求一种具体量的表示方法来清楚地表达“适时”这个概念。研究发现通过围岩“允许变形量”可以确定支护时机，但是，洞室的位移受到多种因素的影响。就某一工程而言，当地质条件、洞室形状与尺寸、施工方法等确定时，主要受到2个因素的影响：

(1) “空间效应”，即掌子面约束作用所产生的影响。距掌子面越近，影响越大，距掌子面越远，影响越小，到达某种距离后影响基本上可以消除。

(2) “时间效应”，通常指掌子面约束作用解除后，变形随时间而增大的这一现象。

以上2个因素对一般岩体来说，前者占90%以上，后者占不到10%，所以人们开始探索允许释放位移量和掌子面进尺之间的关系。 随后经过很多学者探索，2003年，Unlu and Gercek[3]通过大量实验提出了能准确反映围岩塑性、而且塑性区影响的隧道位移随开挖面(掌子面)的变化曲线——LDP曲线，公式如下：

(1)

(2)

(3)

(4)

式中：RP为隧洞中心到塑性区最外边缘的距离，m；u0为掌子面的径向位移，m；Rt为隧洞半径，m；X为开挖断面到掌子面的距离，m；umax为最大径向位移，m。

1.2 应力释放法和弹性模量折减法理论

岩体在开挖过程中，开挖荷载是隧洞施工期的主要荷载。实际的岩体开挖过程是开挖岩体部分的应力释放过程，对于开挖的模拟可以简单地假定为在边界上施加保持围岩单元位移不变的外力荷载的反作用力，即工程所谓的“反转作用力”[4]，亦即在开挖边界上作用与原有支撑力相反的荷载来模拟开挖。各次开挖后地应力释放产生的等效结点荷载为：

(5)

式中：σj为第j-1次开挖引起地应力重分布后的应力场；[Bi]为开挖单元i的几何矩阵；a为地应力释放系数。

根据文献[5]的研究成果，在对隧道开挖二维模拟过程中，弹塑性力学特征参数(变形模量E、泊松比μ，内粘结力c、内摩擦角φ等)对洞室位移变化影响的灵敏度分析显示，变形模量对位移的影响是占绝对优势的，因而在二维仿真模拟分析过程中，将应力释放的综合因素可以通过变形模量的变化近似地体现出来，即弹性模量折减法。

2 分析思路

本文基本分析思路如下：

(1) 针对德尔西水电站引水隧洞Ⅲ(D)类围岩通过式(4)计算出位移随掌子面的变化曲线——LDP曲线，进而计算出“允许变形量”，即最佳支护时机，亦即围岩在达到“允许变形量”之前无需支护，是通过“允许变形量”来控制支护时机；

(2) 通过应力释放和弹性模量折减方法模拟隧洞开挖、洞周位移缓慢变形的过程，求出随应力释放以及弹性模量折减位移变化过程曲线，根据计算出的“允许变形量”寻找对应的应力释放系数和折减弹性模量，此为“适时”的支护时机，即在此时，施加锚喷支护；

(3) 对比及时支护和适时支护围岩变形和喷锚支护结构受力情况。

3 工程应用

德尔西水电站主要由首部枢纽、引水系统、发电系统和输变电系统组成。引水系统主要建筑物包括进水口、引水隧洞、调压井和压力管道。引水隧洞直径为4.1～4.9 m，全长约8 553.5 m。

引水隧洞岩体工程质量类别为Ⅱ类(A+B)、Ⅲ类(C+D)和Ⅳ类(E),本文选取具有代表性的Ⅲ(D)类围岩进行分析。围岩参数见表1，支护材料参数见表2。

表1 围岩计算选取参数表

表2 支护材料力学参数表

3.1 模型建立

本文采用Phase2软件进行计算，Phase2软件是 Rocscience 公司开发的专门模拟地下岩体开挖工程应力及应变的二维有限元软件，其分析步骤分3个阶段，即前处理、求解和后处理。同其它有限元软件相比，该软件具有建模简单、网格划分容易和后期处理功能强大等特点，尤其在模拟地下洞室开挖时有突出优势，可以模拟隧洞开挖及开挖后对围岩和支护结构的影响。

由于引水隧洞布置在左岸雄厚的山体中，一般隧洞埋深100～500 m，取平均埋深为300 m，根据海姆假说[6]，如果岩体是理想的塑性体，而且埋深较大，岩体就处于近似静水压力状态，应力的大小等于其上覆岩体的自重，而且岩体中各个方向的应力均相等。所以，围岩初始地应力场为σ1=σ2=σ3=γh=8MPa

模型模拟范围取5倍洞径，模型边界为全约束位移边界条件(见图1)。模型计算采用Mohr-coulomb准则。

图1 计算模型图

3.2 最佳支护时机确定

(1) 应力折减法

首先采用20个计算阶段进行应力折减计算，通过不同的计算阶段进行应力折减，从而实现隧洞应力逐步释放，最终得出位移随应力释放的变化曲线。计算模型如图2。

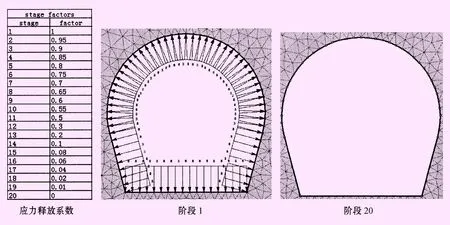
图2 应力折减法计算模型图

此处计算阶段是人为定义的，计算阶段主要是为了表示隧洞应力释放过程。定义的计算阶段越多，则应力释放过程模拟越细致。本文定义20个计算阶段来实现隧洞开挖后围岩的应力释放过程，其中阶段1表示围岩应力没有释放，即图2中应力释放系数为1；中间阶段应力释放系数逐渐递减，直到最后一个阶段，本文中阶段20表示隧洞应力释放完成，即图2中应力释放系数为0。

通过计算得知，最大位移发生在底拱，计算出底拱最大径向位移umax=5.16 mm和隧洞中心到塑性区最外边缘的距离RP=3.478 m，如图3和图4。

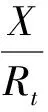
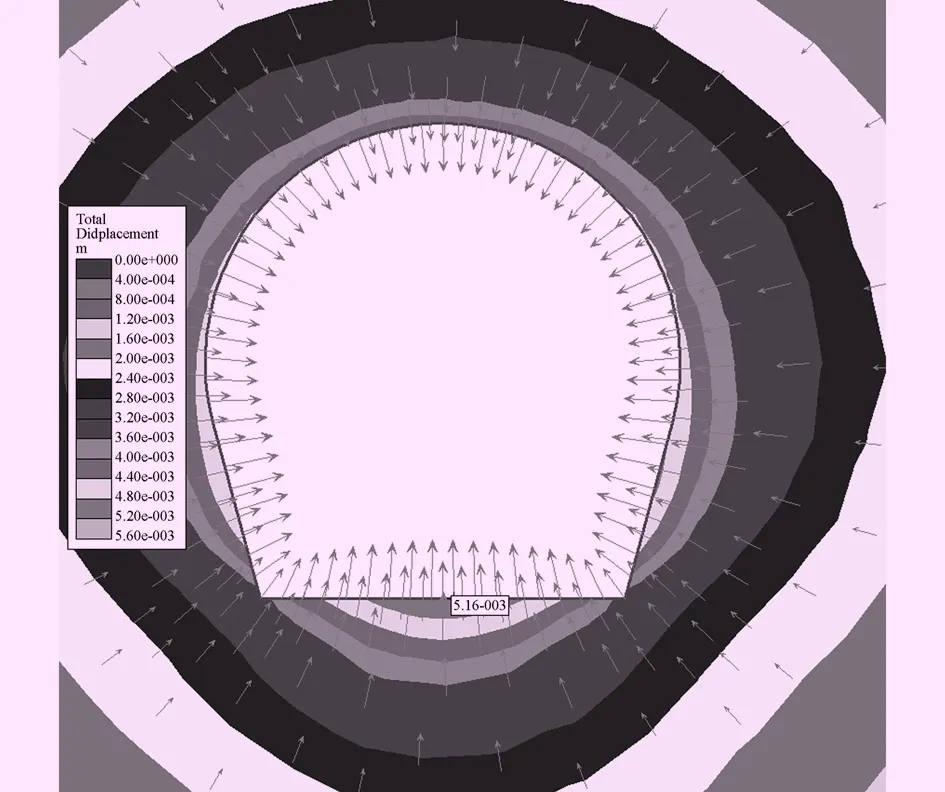
图3 围岩位移图

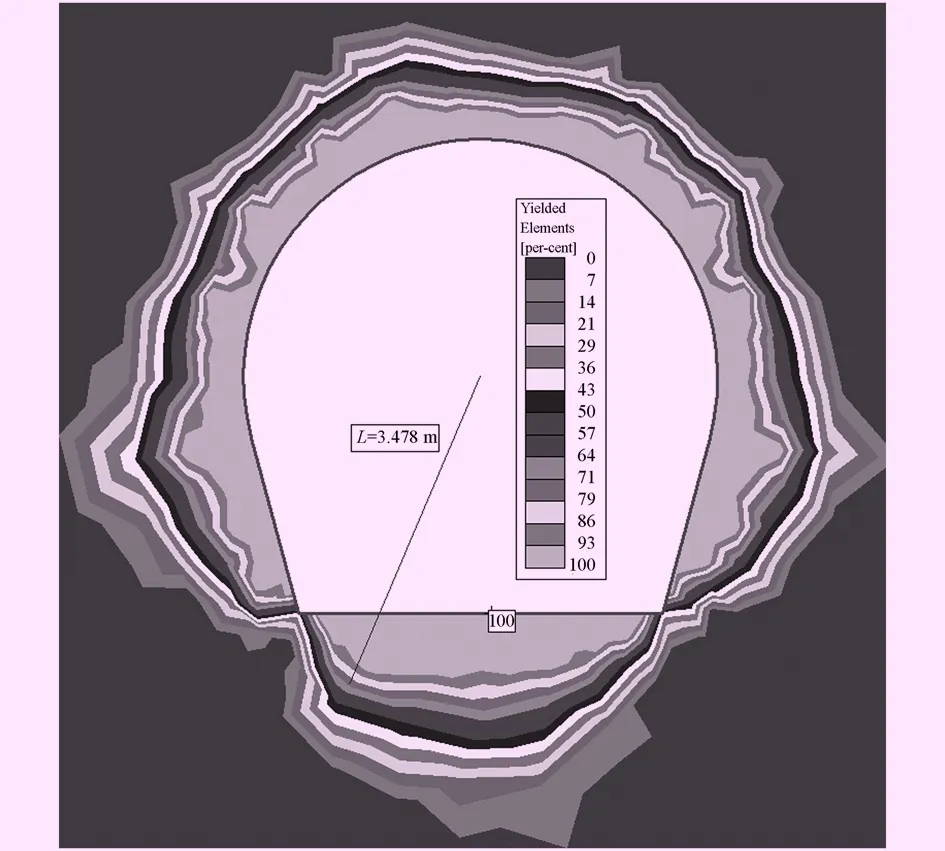
图4 围岩塑性区图

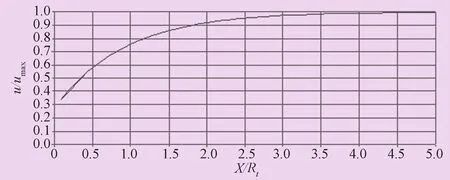
图5 LDP曲线图

由LDP曲线可见，开挖断面到掌子面的距离越大，隧洞变形越小，通过这一方法可评估距掌子面一定距离处洞壁位移的收敛情况、应力释放程度及所需的支护力，借此来控制围岩变形和支护压力。

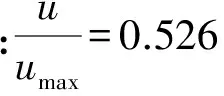
由底拱最大位移随应力释放阶段变化(见图6)可以看出，在应力释放11～12阶段之间，接近12阶段，隧洞底拱径向位移接近允许释放位移2.72 mm，即应力折减系数取0.3～0.5时，为最佳支护时机。

图6 不同阶段的底拱最大位移变化曲线(应力折减)

对应力折减系数进行0.3～0.5之间的细化，得出底拱最大位移随计算阶段的变化曲线，见图7，找到最佳支护阶段为14～15，应力释放系数最终确定为0.31。

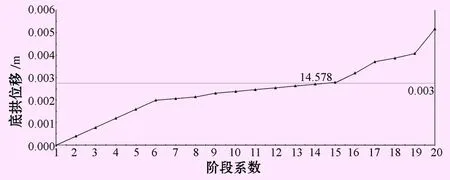
图7 不同阶段的底拱最大位移变化曲线(应力细化后)

(2) 弹性模量折减法

允许释放位移和前面计算方法一样，同样可以得出允许释放位移为2.72 mm。

上节应力折减系数为0.31，锁定开挖部分围岩弹性模量折减系数接近0.31，所以对弹性模量进行3 000～2 000 MPa之间的细化计算，模型如图8。

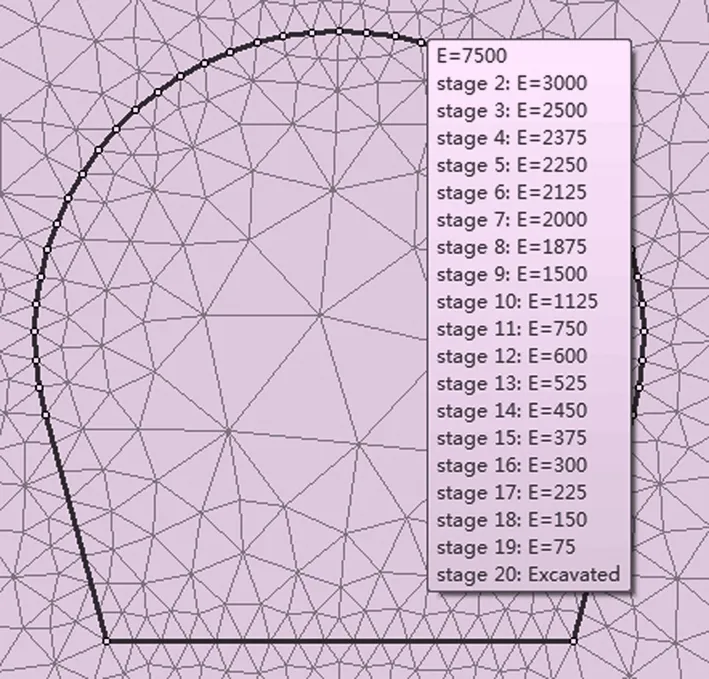
图8 弹性模量折减模型图

采用图8中弹性模量折减方式，底拱最大位移随阶段变化曲线(如图9)，找到最佳支护阶段为2～3，接近第3阶段，最终确定开挖部分围岩的弹性模量折减为2 600 MPa。

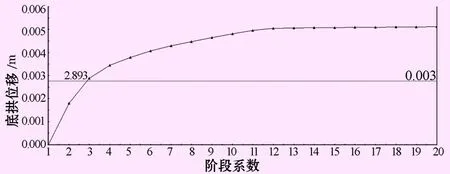
图9不同阶段的底拱最大位移变化曲线(弹性模量折减)

4 不同支护时机特性对比

(1) 特性对比

通过计算，分别得出应力折减法和弹性模量折减法的围岩支护时机，与及时支护相比，围岩的位移、塑性区分布以及支护结构的受力情况，总结如下：

1) 位移情况。开挖释放后，洞周位移向洞内变形，且位移呈现环状分布趋势，从内向外逐渐减小，位移范围在0～5 mm之间，由于顶拱是拱形，受力条件较好，同时顶拱施作锚杆支护，最大位移位于底拱，不同支护时机的底拱位移最大值见表3。

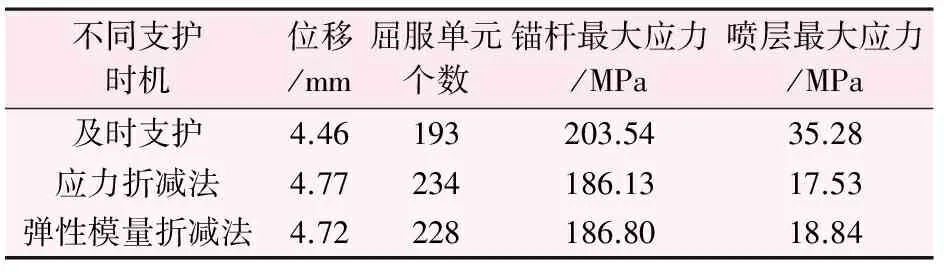
表3 不同支护时机结果对比图表

2) 塑性区情况。开挖释放后，洞周塑性区呈现环状分布，但是由于顶拱是拱形，受力条件较好，同时顶拱施作锚杆支护，下部边墙和底拱塑性区厚度大于顶拱塑性区厚度，塑性区厚度在0～0.7 m之间，不同支护时机的塑性屈服单元个数见表3。

3) 支护结构的受力情况。施作锚喷支护后，锚杆应力从洞周向外均匀递减，锚杆受力范围20～204 MPa，锚杆受力最大部位位于洞周顶拱；喷层轴力沿着洞周分布比较均匀，轴力范围在0.5～3 MN之间，喷层弯矩图分布情况为顶拱弯矩较小，边墙下部弯矩大，弯矩范围在-0.03～0.02 MN.m，喷层最大应力部位位于边墙下部。不同支护时机锚杆应力和喷层应力最值见表3。

(2) 优化结论

1) 及时支护能够及时阻止围岩开挖后的变形和塑性区的扩展，其位移和屈服单元数相对于其他2种支护时机的较小，但是适时支护的位移和塑性区增大范围较小，不会引起围岩的破坏；

2) 及时支护情况下支护结构承担了围岩开挖后所有荷载，所以其支护结构受力明显大于其他2种支护时机，而且喷层的受力超过了喷层的抗压强度21 MPa，需要采用加厚喷层等支护措施；其他2种支护时机的支护结构受力较小，满足锚杆和喷层的受力要求，因此采用适时支护可以优化支护结构；

3) 应力释放法和弹性模量折减法的围岩位移及支护结构受力基本相当，证明了采取任意一种方法进行合理支护时机模拟都可以达到优化支护结构的目的。

5 结 语

最佳支护时间点在工程上是节约工程材料降低工程造价的理想点，这一时刻可以保证工程材料最省和工程造价最低。本文通过德尔西水电站Ⅲ(D)类围岩段隧洞开挖围岩稳定性数值模拟，采用量化、清晰易懂方式向咨询工程师解释了引水隧洞围岩支护时机的问题，并证明了合理地选择支护时机可以优化支护结构，弥补了以往围岩最佳支护时机的不确定性、不准确性和经验性的缺点，使洞室开挖支护的优化设计和安全性评价成为可能。

[1] 韩瑞庚.地下工程新奥法[M].北京：科学出版社,1987.

[2] 刘长武.煤矿软岩巷道的锚喷支护同新奥法的关系[J].中国矿业,2000，1(1)：61-64.

[3] Hoek,E.,Carranza-Torres,C.,Diederichs,M.S.and Corkum.Integration of geothechical and structural design in tunnelling[C]//Proceedings University of Minnesota 56th Annual Geotechnial Engineering Conference.Minneapoils,29 February 2008,1-53.

[4] 王伟.狮子坪水电站不良地质隧洞开挖方式与支护参数优化研究[D].武汉:武汉理工大学,2007.

[5] 陈方方.地下洞室弹塑性仿真反分析研究[D].西安:西安理工大学,2004.

[6] 王树洪.高地应力高外水压隧洞围岩稳定和支护结构研究及应用[D].南京：河海大学,2004.

[7] R. K. Goel,Bhawani Singh， Rock mass classification[M].ELsevier Science Ltd., 1999.

Application of Phase 2 Software in Support Time of Surrounding Rock in Tunneling

HE Xin, CAO Huai-yuan, LIU Yong-zhi, LIU Jie-yu

(POWERCHINA Xibei Engineering Corporation Limited, Xi'an 710065,China)

New Austrian tunneling method allows deformation of surrounding rock, support is provided at Proper Time. Under the precondition of securing stability of surrounding rock, support measures is decreased. In this paper, Proper Time is determined by application of stress release method and elastic module reduction method through Phase 2 software. Accordingly, theory of new Austrian tunneling method is applied in design of support structure of the headrace tunnel of Delsi Hydropower Project. By application of quantitive, clear and simple means, it verifies that the proper support time allows to optimize support structure and reduce investment as well. This is practical for the design of support structure of tunneling works.

tunnel; support time; new Austrian tunneling method (NATM); displacement; Phase 2; Delsi Hydropower Project

2015-04-15

何欣(1987- )，女，陕西省户县人，助理工程师，主要从事水工和岩土设计工作.

TV222.2;TV554

A

10.3969/j.issn.1006-2610.2015.03.014