后掠展长组合变形飞行器动力学建模

王志刚, 徐聘，周嘉星， 李娜英

(1.西北工业大学 航天学院, 陕西 西安 710072;2.航天飞行动力学技术国家重点实验室, 陕西 西安 710072;3.北京机电工程研究所 先进制导控制技术国防重点实验室， 北京 100074)

后掠展长组合变形飞行器动力学建模

王志刚1,2, 徐聘3，周嘉星1,2， 李娜英3

(1.西北工业大学 航天学院, 陕西 西安 710072;2.航天飞行动力学技术国家重点实验室, 陕西 西安 710072;3.北京机电工程研究所 先进制导控制技术国防重点实验室， 北京 100074)

为了分析变形飞行器的动态响应特性,针对后掠展长组合变形飞行器建立了动力学模型。将变形飞行器看作一个完整的多刚体系统,建立变形飞行器组合变形方程,采用多刚体理论建立了能完整描述飞行器变形过程的动力学模型。该动力学模型适用于普遍情况下的后掠展长变形飞行器。

变形飞行器; 动力学建模; 多刚体系统

0 引言

传统飞行器的固定构型决定了其空气动力特性,而空气动力特性又是影响飞行性能的重要因素,因此固定构型约束了飞行器的性能。变形飞行器能够在飞行中主动改变构型以适应宽广变化的飞行环境,不仅能够提高飞行器的飞行性能,还可以减少飞行器的研发数量、降低研发支出。基于上述优点,国内外学者对变形飞行器的动力学建模、仿真、控制及飞行试验等进行了理论及应用研究。

Seigler等[1-3]研究了变形飞行器的建模与控制问题,分别基于质点系、多刚体系统和刚体-质点系统物理模型建立了3种变形飞行器的动力学方程;分析了飞机变形过程中的动力学响应[3]。An等[4]研究了变后掠飞机变形过程中的动态响应,建立了飞机的动力学方程,分别分析了无控情况下的变后掠、有自动驾驶仪的变后掠、加速与减速过程中的变后掠的动态响应过程,以及静态力变化和非定常气动力对变后掠动态响应过程的影响。金鼎等[5]针对一种飞翼布局折叠机翼变体飞机方案,建立了相应的研究模型。张公平等[6-7]基于集中质量假设,利用动量定理及动量矩定理,构建了变翼导弹的多体动力学模型。徐孝武等[8]研究了多刚体系统动力学理论应用于折叠机翼变体飞机动力学建模方法,考虑变体飞机为一个完整的多刚体系统,采用牛顿-欧拉方法建立了能够完整描述变形过程的动力学模型。上述研究均针对单一变形方式,没有考虑多种变形同时存在的情况。

本文针对后掠展长组合变形飞行器,根据后掠展长变形特点建立组合变形方程,并基于多刚体动力学理论中的牛顿-欧拉法开展动力学建模研究。

1 多刚体系统模型

本文研究的变形飞行器如图1所示,该飞行器具备在飞行过程中改变机翼后掠角和展长的能力。飞行器由机体和机翼组成,每一侧的机翼分为内外两段:内段翼通过圆柱铰与机体相连,可以在机翼平面内转动改变后掠角;外段翼通过滑移铰与内段翼相连,可以沿内段翼滑动改变机翼的展长。基于多刚体系统假设,可以将变形飞行器抽象为由5个刚体组成的多刚体系统,如图2所示。图中:Oi为各刚体Bi的质心;Ji为连接各刚体的铰链。

图1 变形飞行器结构示意图Fig.1 Structural sketch of morphing aircraft

图2 变形飞行器多刚体模型Fig.2 Multi-rigid-body model of morphing aircraft

为了方便描述变形飞行器的结构,首先对变形飞行器的各个刚体进行编号。规定代表机体的刚体为B1,从刚体B1出发有两条通路分别通往左右机翼。沿着通路,系统内与刚体Bi直接相连且靠近B1一侧的刚体称为Bi的内接刚体,将Bi与其内接刚体连起来的铰称为内接铰;通往与Bi连通的外侧刚体的铰称为外接铰。令每个刚体与其内接铰有相同的序号以及每个刚体的序号大于其内接刚体的序号,如图2所示:刚体B2为右侧机翼内段;B3为外段;刚体B4为左侧机翼的内段;B5为外段。

由Bi的质心Oi指向与Bi关联的任意铰Jj的矢量称为体铰矢量,记作cij：c12为由B1的质心O1指向铰链J2的体铰矢量;c22为由B2的质心O2指向铰链J2的体铰矢量。从刚体Bi的内接铰出发指向Bi外接铰的矢量称为通路矢量,记作dij;刚体Bi的质心相对于机体质心O1的矢量用ρci表示;zi为滑移铰Ji的相对滑移矢量。根据以上定义可知dij=-cii+cij,如d23=-c22+c23。

2 组合变形规律方程

2.1 坐标系定义

(1)机体坐标系O1x1y1z1:原点O1为飞行器机体B1质心;O1x1轴与飞行器纵轴重合,指向头部为正;O1y1轴在与飞行器纵向对称的平面内,垂直于O1x1,向上为正;O1z1轴垂直于x1O1y1平面,方向按右手定则确定。

(2)机翼固连坐标系Oixiyizi:以机翼段Bi的质心Oi为坐标原点;Oiyi轴与机翼平面垂直,向上为正;Oizi轴保持与机翼前缘平行,指向外侧为正;Oixi轴按右手定则确定。

2.2 变形规律方程

后掠展长变形飞行器的变形规律方程为:

(1)

式中:Λr为右侧机翼的后掠角;Λrd为期望的右侧机翼后掠角;下标“r”对应右侧机翼,“l”对应左侧机翼,下标“d”对应期望值;Λl为左侧机翼的后掠角;Λld为期望的左侧机翼后掠角;z3为右侧机翼的展长伸缩量;z3d为期望的右侧机翼展长伸缩量;z5为左侧机翼的展长伸缩量;z5d为期望的左侧机翼展长伸缩量;t为时间。

机翼变形主要影响机翼质心相对于机体质心的矢量ρci。ρci在机体坐标系下的坐标列阵为:

(2)

3 变形飞行器多刚体动力学建模

3.1 基本假设

为简化动力学建模过程,本文作如下假设:

(1)机翼上反角为零;

(2)机翼无安装角;

(3)机翼质量分布均匀;

(4)飞行器存在纵向对称面,且其变形为对称变形。

3.2 受力分析

(1)飞行器整体受力分析

在飞行过程中,如果把飞行器看作一个整体,那么作用在飞行器上的外力主要有空气动力、空气动力矩、发动机推力和重力。

(2)飞行器部件受力分析

对于机体B1,在铰链J2处受到铰链的约束力F2及驱动力矩MG2的作用，在铰链J4处受到铰链的约束力F4及驱动力矩MG4的作用。在飞行器飞行过程中,B1始终暴露在空气中,因此要受到空气动力F1的作用。此外,B1还受到发动机推力T以及自身重力m1g的作用。

对于右侧机翼内段B2,在J2处受到该铰链的约束力及驱动力矩的作用,该约束力和驱动力矩与B1所受的约束力和驱动力矩大小相等方向相反,即B2受到的约束力为-FG2,驱动力矩为-MG2。在铰链J3处B2受到铰链的约束力FG3及驱动力QG3作用。此外,B2同样受到空气动力F2和自身重力m2g的作用。

对于右侧机翼外段B3,在铰链J3处受到铰链的约束力和驱动力的作用,这两个力与B2所受到的约束力和驱动力大小相等方向相反,即B3受到的约束力为-FG3,驱动力为-QG3。此外,B3也受到空气动力F3和自身重力m3g的作用。

对于左侧机翼内段B4、外端B5,由于左右翼对称,其受力分析与右侧机翼类似,不再赘述。

3.3 牛顿-欧拉法动力学建模

对变形飞行器每个刚体Bi(i=1,…,n)建立牛顿-欧拉动力学方程为:

miai=Fai+Fci(i=1,…,n)

(3)

(i=1,…,n)

(4)

式中:ai,Fai,Fci为Bi的加速度、主动力、约束反力;Ii,ωi,Lai,Lci为Bi的中心惯量张量、角速度、主动力对质心的主矢、约束反力对质心的主矢。将以上两式在机体坐标系中投影,得到矩阵形式的动力学方程:

(Fai+Fci)/mi

(5)

Lai+Lci

(6)

将各刚体的动力学方程相加后,可消去各刚体之间的约束力和约束力矩,得到机体坐标系下标量形式的3个力方程和力矩方程如下:

(7)

(8)

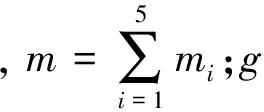
4 结束语

本文将后掠展长组合变形飞行器视为多刚体系统,建立变形规律方程,基于牛顿-欧拉方法建立组合变形飞行器的动力学模型。本文建立的动力学模型适用于普遍情况下的后掠展长组合变形飞行器,为该类型变形飞行器动态响应分析奠定了基础。

[1] Seigler T M.Dynamics and control of modeling aircraft [D].Virginia:Virginia Polytechnic Institute and State University,2005.

[2] Seigler T M,Neal D A,Bae J S,et al.Modeling and flight control of large-scale morphing aircraft[J].Journal of Aircraft,2007,44(4):1077-1087.

[3] Seigler T M,Neal D A,Inman D J.Dynamic modeling of large-scale morphing aircraft[R].AIAA-2006-1893,2006.

[4] An Jiguang,Yan Ming,Zhou Wenbo,et al.The dynamic response of a variable sweep aircraft in the course of changing geometry[R].AIAA-86-2234,1986.

[5] 金鼎,张炜,艾俊强.折叠机翼变体飞机纵向操纵性与稳定性研究[J].飞行力学,2011,29(1):5-12.

[6] 张公平,廖志忠,段朝阳,等.可变形翼战术导弹飞行动力学联合仿真研究[J].航空科学技术,2011(3):71-74.

[7] 张公平,廖志忠,段朝阳,等.可变形翼战术导弹多体动力学特性[J].弹箭与制导学报,2011,31(6):149-151.

[8] 徐孝武,张炜.折叠机翼变体飞机的动力学建模与分析[J].西北工业大学学报,2012,30(5):681-688.

(编辑：李怡)

Dynamic modeling of aircraft with sweep and span combined morphing

WANG Zhi-gang1,2, XU Cheng3, ZHOU Jia-xing1,2,LI Na-ying3

(1.School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2.National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China;3.Key Laboratory of Advanced Guidance and Control Technology, Beijing Electro-mechanical Engineering Institute, Beijing 100074, China)

In order to study the response characteristics of morphing aircraft, dynamic model of aircraft with sweep and span combined morphing was established. Considering a morphing aircraft which can change its wing sweep and span as a complete multi-body system, multi-body theory was used to establish the morphing aircraft’s dynamic model. The dynamic model can be widely used in the analysis of aircraft with sweep and span combined morphing.

morphing aircraft; dynamics modeling; multi-body systems

2014-12-10;

2015-03-23;

时间:2015-06-24 15:03

王志刚(1968-)，男，陕西渭南人，教授，博士生导师，研究方向为飞行动力学与控制; 徐骋(1980-)，男，江苏江阴人，高级工程师，博士，研究方向为导航、制导与控制; 周嘉星(1989-)，男，福建厦门人，博士研究生，研究方向为飞行动力学与控制。

V212.1

A

1002-0853(2015)05-0407-04