剪切式变后掠翼气动特性分析
彭金京,董彦非,2,陈元恺
(1.南昌航空大学 飞行器工程学院,江西 南昌330063;2.西安航空学院 飞行器学院,陕西 西安710077)
0 引言
现代飞机的发明源于人类对鸟类飞行的认识,然而用于产生升力的飞机机翼却无法像鸟类的翅膀那样自由地伸展和舞动,所以也不能像鸟一样适应各种飞行状态。早在1901年,德国的航空先驱古斯塔夫˙韦斯科普夫设计的“秃鹰21”采用单翼面布局,翼面结构设计源于蝙蝠,设计出了可折叠仿生翼型[1]。若干年来,人类从仿生学出发,在智能可变形飞行器领域进行了不懈的探索[2-3]。然而由于受到多学科的技术限制,可变形飞行器的研究一度陷入低潮。近些年来,随着空天领域对多功能、高效能飞行器需求的增强[4]和仿生飞行与智能材料结构研究的发展[5-6],以及材料、传感、计算机、气动、控制等科学技术的高速发展,现代变形飞机的研究又迅速成为空天技术创新领域的热点。现代变形飞机采用智能变形技术,可以解决不同设计点气动布局的矛盾,改善多功能性,针对飞行各阶段的不同要求改变机翼的形状,随马赫数、迎角、大气扰动和机动飞行等飞行条件的改变而自动通过机翼内部的联动机构改变机翼后掠角、翼展和机翼翼型,并采用智能蒙皮组件以保持翼面变化的光滑连续性,使之适应不同的飞行状态,达到实时最优性能。
研究“变后掠”的具体变形方式对气动特性的影响,有利于现代变形飞机的概念设计。传统变后掠翼飞机的变后掠技术采用“旋转变后掠”方式,机翼通过翼根处转轴旋转而改变后掠角。然而这种方式在变后掠过程中机翼的翼型发生变化,且翼尖并非沿流向。一般而言,机翼设计方法是在某一特定飞行状态下优化出的机翼形状,因此翼型的改变对飞机飞行气动特性的改善不利,并且为了其气动特性,甚至须使用类似气囊的部件来补充机翼小后掠角时后缘缺失的部分。因此,本文采用一种新的变后掠方式——“剪切式变后掠”[7]为研究对象,通过数值模拟其在飞行包线内的流场,计算出气动数据,从而分析其在宽广速域内的气动特性,为实现飞机在不同飞行状态下保持最优性能奠定基础[8-9]。
1 飞机外翼段剪切式变后掠设计
“剪切式变后掠”的方式与传统的“旋转变后掠”方式不同,飞机在飞行过程中,若改变飞行任务状态,机翼则自适应改变机翼后掠角,将机翼各展向位置的翼剖面进行线性规律的流向平移,越靠近翼尖平移量越大,类似于材料力学中的“剪切变形”,可实现后掠角的变化,并且翼尖沿流向,扰流场结构影响小;机翼内部的智能材料驱动肋板中植入智能驱动元件来改变机翼剖面,从而适应不同飞行任务状态下的气动特性。图1给出了“剪切式变后掠”方式示意图。
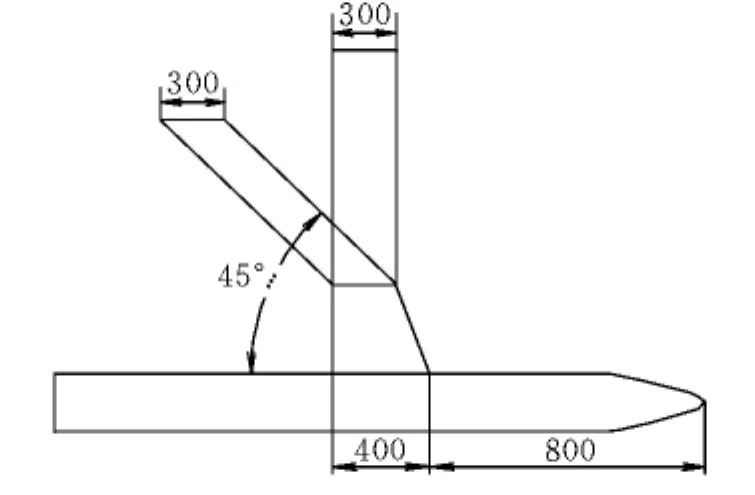
图1 剪切式变后掠方式示意图Fig.1 Schematic diagram of shearing variable-sweep airfoil mode
为了减少因机翼后掠带来的气动中心改变而产生的气动中心移动导致的负面作用,试验模型机翼采用内外翼两段式结构,内翼约为机翼半展长的30%,与机身固定,外翼绕内翼剪切变后掠,从而获得较好的性能[8-9]。
根据总体需求分析可知,地面最大后掠角为60°,飞行过程中外翼段后掠角从0°改变为45°;内翼段翼型采用NACA64-215,外翼段翼型采用NACA64-110,内翼段前缘后掠角固定为 12°[10]。
2 飞机变后掠机翼准定常扰流数值模拟方法
本文采用三角函数规律的变后掠方式:
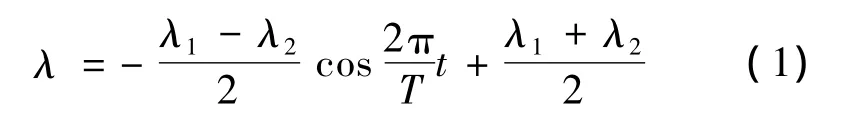
式中:λ为t时刻的后掠角;λ1为最小后掠角;λ2为最大后掠角;T为运动周期。
模拟计算中采用可压缩流动 Reynolds平均Navier-Stokes方程[10-11]:
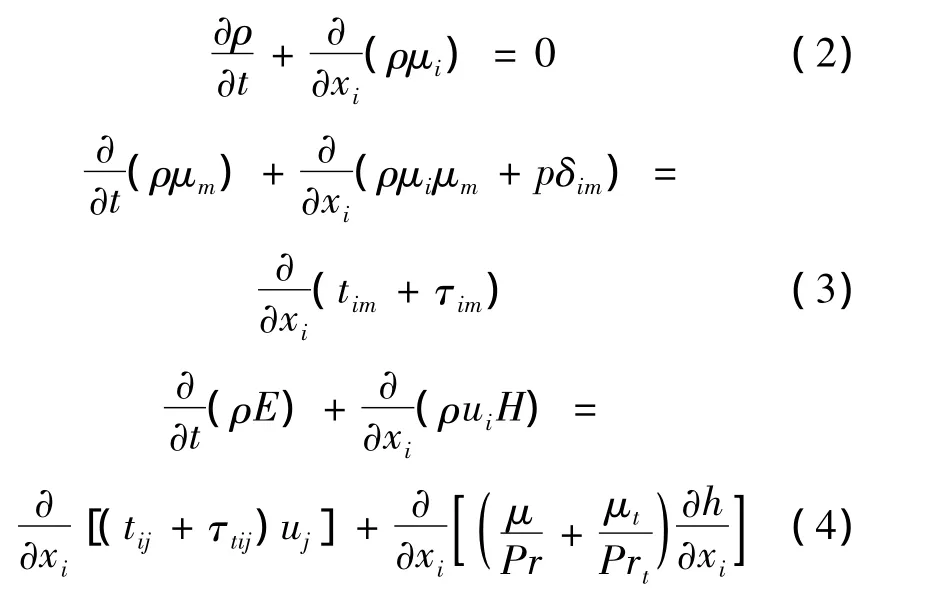
式中:τtij为雷诺应力;μt为涡粘性系数。
本文模型在近壁处采用Wilcox k-ω模型,边界层边缘和自由剪切层采用k-ε模型(k-ω形式),其间通过一个混合函数来过渡。k-ω湍流模型主要求解湍动能k及其比耗散率ω的对流输运方程,对于SST k-ω双方程模型,其湍动能输运方程为[12]:
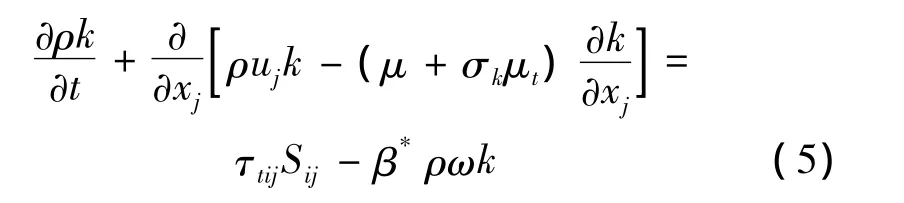
式中:ρ为平均流密度;k为湍动能;β*为模型常数,取0.09;ω为湍流比耗散率。
湍流比耗散率方程为:
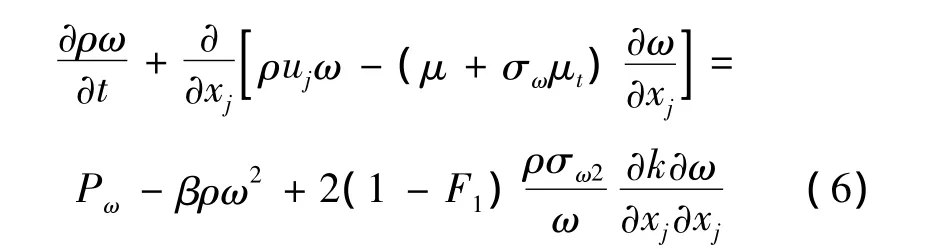
式中:Pω为生成项。
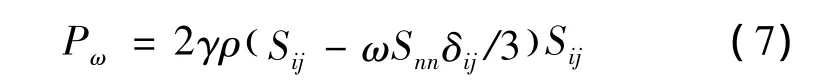
雷诺应力的涡粘性τtij模型为:
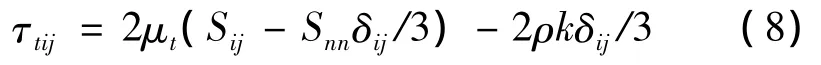
式中:Sij为平均速度应变率张量;δij为克罗内尔算子。
湍流比耗散率ω与湍动能k及平均流密度ρ一起,可通过下式得到涡粘性系数:
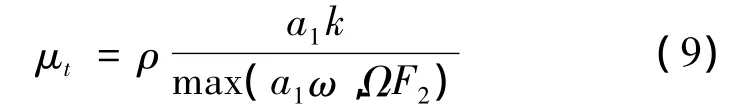
式(5)和式(6)由近壁处的Wilcox k-ω模型输运方程及边界层边缘和自由剪切层的k-ε模型输运方程混合而成,这个混合函数关系式为:
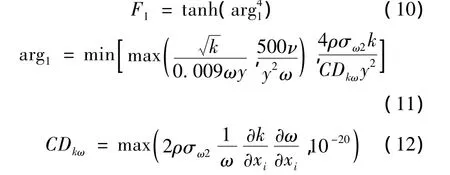
式(9)中还包含以下混合函数关系:
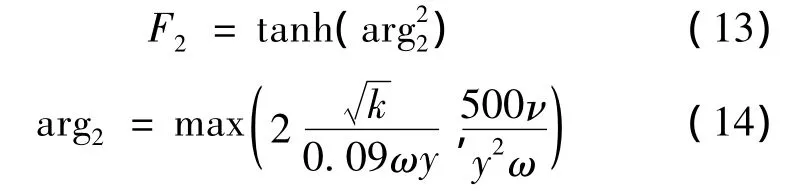
3 ANSYS数值仿真气动特性分析
本文针对图1所示的“剪切式变后掠”方式进行计算,对于机翼准定常变后掠的情形,可以直接计算若干固定后掠角布局的气动特性。4种后掠角布局如图2所示。
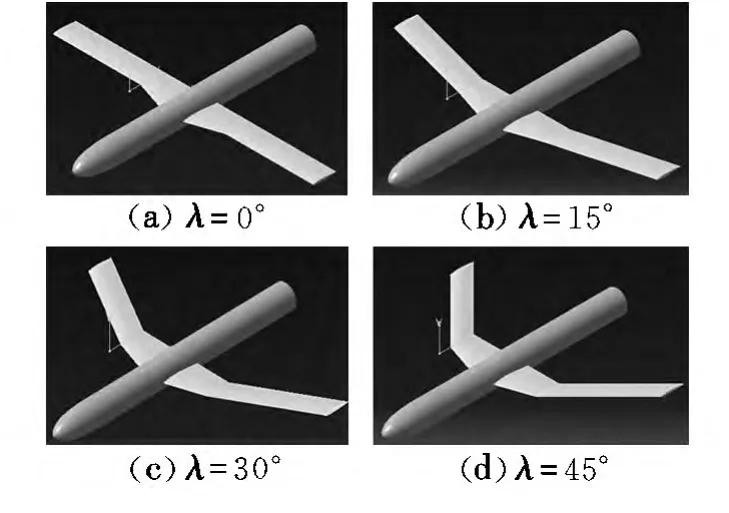
图2 后掠角布局Fig.2 Sweepback layout
在ANSYS数值仿真分析时,自由来流马赫数范围设定为0.4~1.2;内边界采用无滑移壁面条件,外边界采用自由流边界条件;计算网格为结构与非结构混合网格,近壁区域采用三棱柱网格,其余区域为四面体网格,并且对局部网格进行了加密处理,网格单元数为70万左右。图3给出了Ma分别为0.4,0.8和1.2时,4种布局方式下迎角对升阻比的影响。
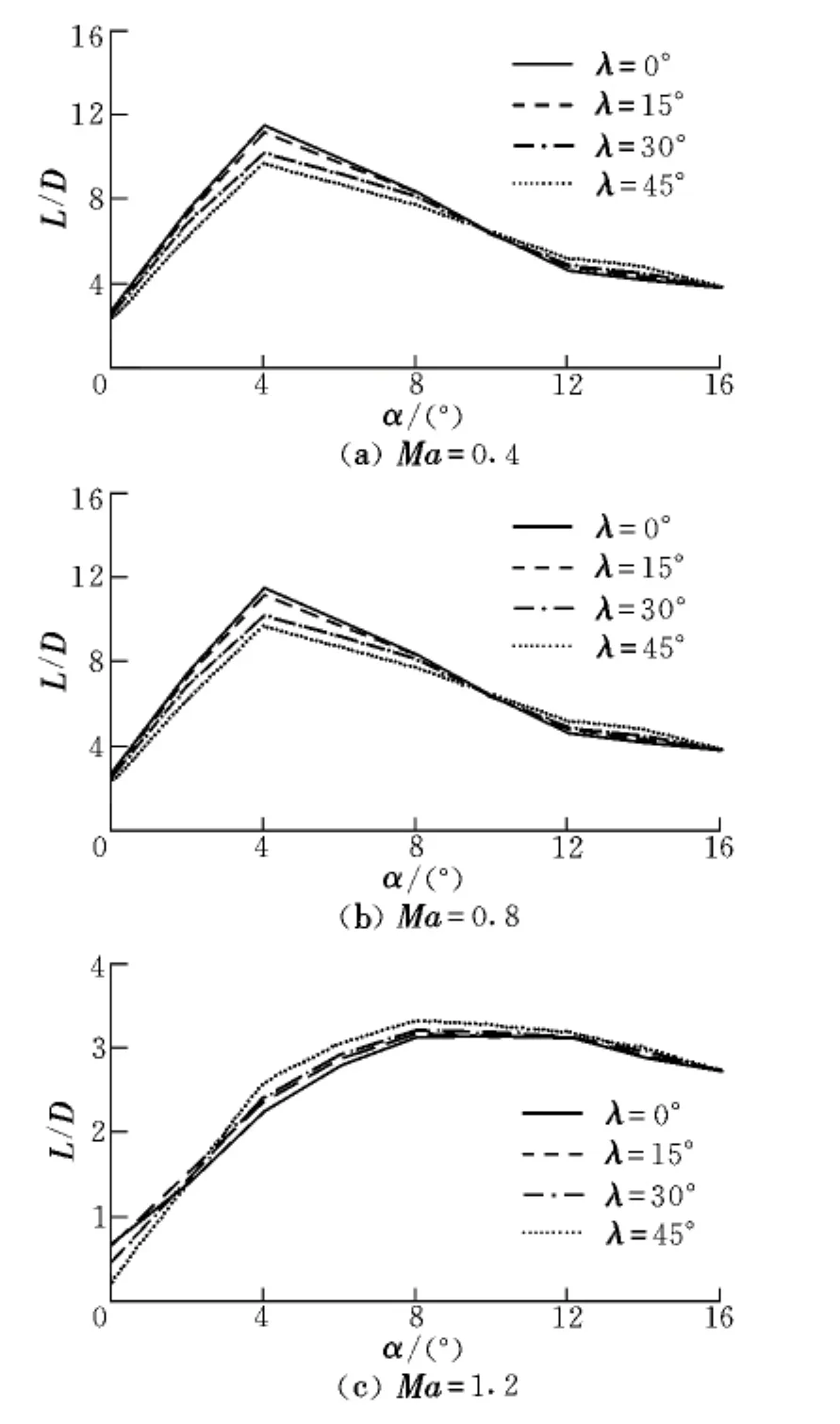
图3 迎角对升阻比的影响Fig.3 Influence of angle of attack on lift-to-drag ratio
从图3中可以看出,对于4种不同后掠角布局,在低马赫数时后掠角为0°和15°的升阻比较大,气动特性更好;而在跨声速和超声速时,后掠角较大的30°和45°升阻比在多数迎角范围内较大,气动特性更好。可见在跨声速和超声速时大后掠角有益于飞机的气动特性,这对于高速巡航的飞行器而言,是一种优势。
分析飞行器不同后掠角布局的气动特性还需要分析其跨声速域飞行的情形。图4给出了4°迎角时4种不同后掠角布局在不同马赫数下的气动特性。由图4可知,大后掠角的翼身组合体在宽广速域内优于小后掠角的翼身组合体,既体现在升阻比,也体现在阻力系数。对于小后掠角(λ≤30°)布局,在亚声速(Ma≤0.7)时,有着比大后掠角(λ=45°)更优的升阻比,对应的升力系数也更优。这种气动特性对可变后掠飞行器具有一定意义:低速起飞和着陆时,飞行器采用0°后掠角布局,此时有着较大的升力特性和较大的升阻比;而在低亚声速时,后掠角以准定常方式增大;在跨声速和超声速机动飞行时,飞行器采用“剪切变后掠”45°后掠角布局,此时不但有着高的气动效率,而且还有低阻力特性。这种现象产生的原因主要是飞机在跨声速和超声速阶段飞行时产生的激波阻力急剧上升,而大后掠角有效地延迟了激波的生成,并且“剪切变后掠”方式的翼尖沿流向,相对于“旋转变后掠”有效地减少了翼尖涡和扰流,对于提高升力和减少阻力是极为有利的。因此,根据本文分析计算,并考虑实际机翼设计中的工程问题,得出机翼最优后掠角变化规律如图5所示。
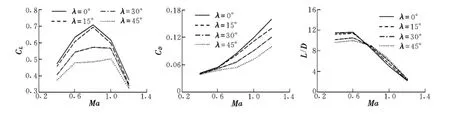
图4 不同马赫数下的气动特性(α=4°)Fig.4 Aerodynamic characteristics at different Mach numbers(α =4°)
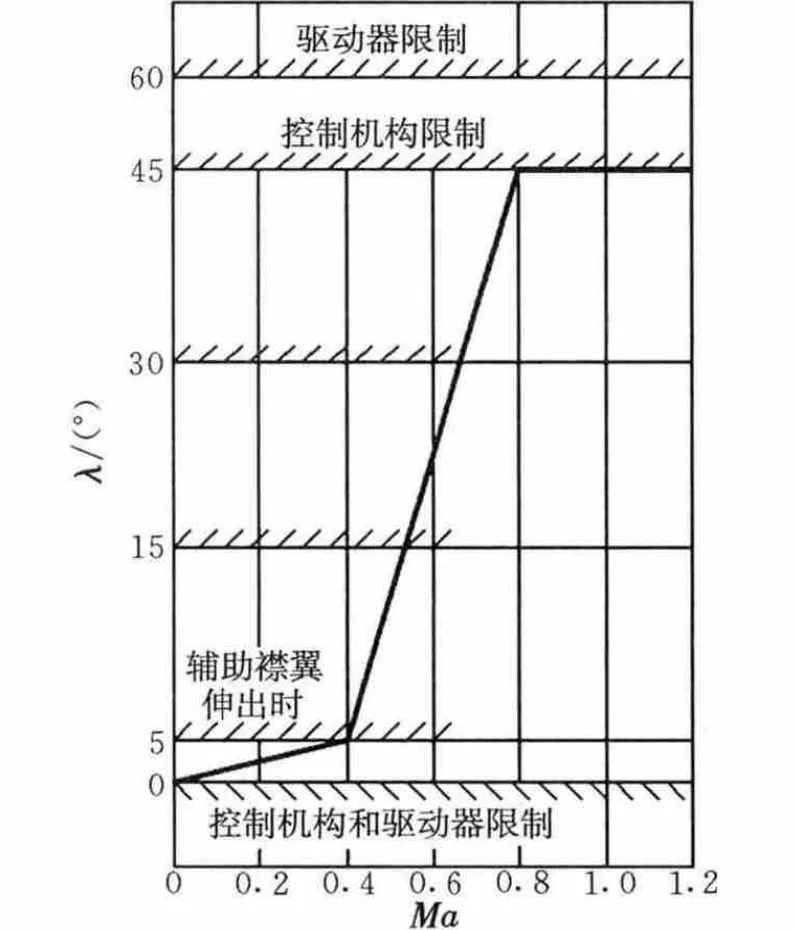
图5 机翼后掠角变化规律Fig.5 Changing rules of wing sweepback
4 结论
总结本文对“剪切式变后掠”方式的气动特性的研究分析,得到以下结论:
(1)“剪切式变后掠”方式可以有效地兼顾飞行器不同飞行状态下较优的气动特性,而采用分段式机翼可以有效地减小变后掠带来的气动中心后移的负面影响。
(2)在亚声速阶段,4种不同布局的阻力系数增加缓慢;而在跨声速阶段,由于产生了局部激波,阻力系数剧增,此时大后掠角有效地延缓激波的产生。相对于小后掠角布局的翼身组合体,大后掠角布局翼身组合体的阻力系数增加较为缓慢,从而使得升阻比更优,这对需要高亚声速和超声速飞行的飞行器而言,有一定的工程应用价值。
(3)与传统的“旋转变后掠”方式相比,“剪切变后掠”方式翼尖方向沿流向,对流动分离和翼尖涡的产生有着积极的影响。
(4)“剪切变后掠”方式对飞机变后掠部件的结构、蒙皮、驱动、控制方面提出了较高的要求和较大挑战,因此,在后续的研究中需要对飞机变后掠机构的应力进行详细的分析,使得“剪切变后掠”方式更具有研究和实践意义。
本文研究结论是基于指定高度下的数值仿真结果得到的,未来有待通过风洞试验和飞行实践验证;同时,需要进一步研究飞行高度的影响,以得到更全面的结论。
[1] 李邦.他比莱特兄弟飞的早[J].航空知识,2014(7):60-61.
[2] Bowman J,Sanders B,Cannon B,et al.Development of next generation morphing aircraft structures[R].AIAA-2007-1730,2007.
[3] Gandhi N,Cooper J,Ward D,et al.A hardware demonstration of an integrated adaptive wing shape and flight control law for morphing aircraft[R].AIAA-2009-5890,2009.
[4] Seigler T M,Neal D A,Bae Jae-Sung,et al.Modeling and flight control of large-scale morphing aircraft[J].Journal of Aircraft,2007,44(4):1077-1087.
[5] Hedenstrom A,Johansson L C,Wolf M,et al.Bat flight generates complex aerodynamic tracks[J].Science,2007,316(5826):894-897.
[6] Muijres F T,Johansson L C,Bareld R,et al.Leding-edge vortex improves lift in slow-flying bats [J].Science,2008,319(5867):1250-1253.
[7] 陈钱,白鹏,尹维龙,等.飞机外翼段大尺度剪切式变后掠设计与分析[J].空气动力学学报,2012,31(1):40-46.
[8] 董彦非,陈元恺,彭金京.可变后掠翼技术发展与展望[J].飞行力学,2014,32(2):97-100.
[9] 陈元恺,董彦非,彭金京.变后掠翼身组合体阻力特性分析[J].飞行力学,2014,32(4):308-311.
[10]顾诵芬,解思适.飞机总体设计[M].北京:北京航空航天大学出版社,2001:27-41.
[11]丁祖荣.流体力学[M].北京:高等教育出版社,2003:91-93.
[12] 周俊波,刘洋.FLUENT6.3流场分析从入门到精通[M].北京:机械工业出版社,2012:11-12.

