基于ARMA/ROM的颤振边界模拟和快速预测
马艳峰,贺尔铭,李俊杰,曾宪昂,唐长红
(1.西北工业大学 航空学院,陕西 西安710072;2.西安飞机设计研究所 强度设计研究所,陕西 西安710089;3.西安飞机设计研究所 总师办,陕西 西安710089)
0 引言
使用CFD技术对气动弹性进行分析能够显著提升计算精度和应用范围。CFD技术在时空维上对气体流动的刻画愈细致,则非定常气动力系统的维数就愈高,直接导致了气动弹性研究计算量大、分析周期长的结果。因此,发展非定常流降阶模型(ROM)已成为一个较为活跃的研究领域,基于CFD技术的非定常气动力降阶模型,可以快速求解系统对任意输入的响应,不必重新运行CFD代码[1]。
依据非定常CFD解的动态线性化假设,目前已经发展了很多的降阶建模技术。其中包括:本征正交分解(POD)[2-3]、Volterra 级数方法[4-6]、神经网格模型、自回归滑动平均(ARMA)模型方法[7]。ARMA模型作为系统辨识的一种通用模型结构,多用于辨识MIMO系统。ARMA模型形式简洁,可准确地描述非线性系统,鉴于应用的准确性和便捷性,气动力的ARMA/ROM在气动弹性分析方面得到了较多的应用。Cowan等[8]利用 ARMA模型结构基于一组CFD的非定常数值解拟合了线性系统的系数。Gupta等[9]将ARMA/ROM应用于高超声速飞行器复杂系统的颤振分析,体现了该方法在工程应用方面的潜力。国内方面,张伟伟等[10]进行了基于ARMA气动力辨识的高效高精度颤振计算研究。
本文系统地给出气动力ARMA/ROM的实现过程,并将之应用于AGARD445.6机翼的跨声速颤振研究。非定常气动力方面,采用位移输入作为训练输入,分别使用Euler和Euler/附面层耦合的方法完成ROM训练过程并获得训练输出,基于Matlab编程实现ARMA模型的参数估计,并进行气动力模型的验证[11-12]。上述气动力ROM的建立过程简便可靠,一定程度上体现了工程应用的特点。
1 ARMA模型降阶方法
基于动态线性化假设,以颤振为代表的气动弹性稳定性问题中,非定常气动力子系统可视为线性时不变系统。因此,可以将气动弹性计算中的非定常CFD求解器视为一个待辨识的动力系统,以结构的模态位移作为输入,广义气动力作为输出。
1.1 过滤脉冲信号
使用脉冲信号激励对系统的动态特性进行充分激励,选择了物理上易于实现的多正弦叠加信号。全阶计算的气动弹性方法用于计算脉冲信号激励后的训练数据。信号的表达式为:
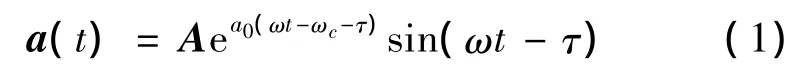
对于AGARD445.6来说,脉冲信号的参数选择为:α0= -0.1,ωc=3.05,τi=0。
使用Euler/BL全阶气动弹性方法,通过上述的多正弦叠加信号,逐级激励前四阶结构模态。AGARD445.6机翼(Ma=0.901)的前四阶滤波脉冲输入信号和系统的广义气动力的响应如图1和图2所示。由图可见,ARMA/ROM的各阶仿真输入、输出和CFD直接模拟结果吻合良好。这表明,对于涉及复杂振型的三维机翼,气动力ARMA/ROM的精度仍然较高。需要说明的是,本文中对广义气动力和广义位移的各变量及过程变量,均进行了无量纲化处理。
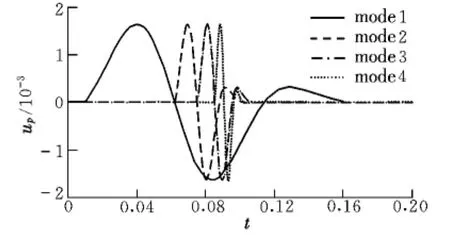
图1 滤波脉冲信号输入Fig.1 Staggered sequence of FIM input signals
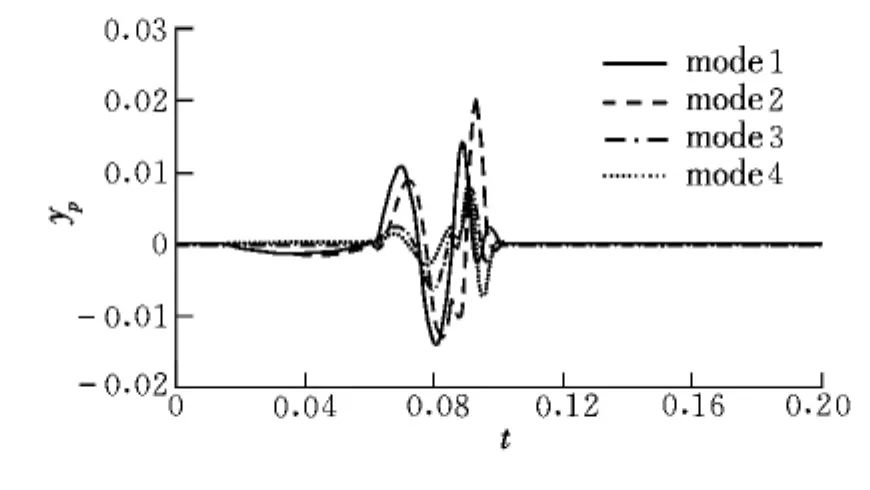
图2 广义气动力响应Fig.2 General aerodynamic force responses
1.2 非定常气动力降阶模型
以颤振为代表的气动弹性问题中,非定常气动力模型可表示为离散的线性状态空间,其差分方程表达式为:
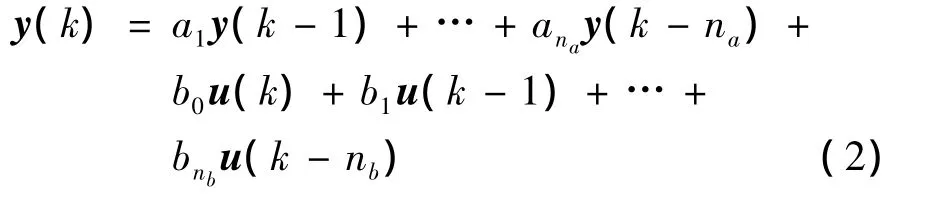
在非定常流体动力学中,广义位移作为系统输入,广义气动力作为系统输出。对于结构的N阶模态,结构的运动可表示为:
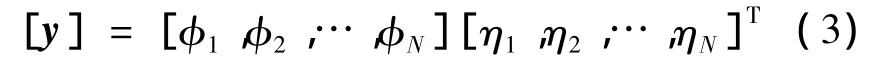
式中:φ为模态向量;η为模态位移。由式(2)和式(3)可得:

式中:q=1,…,N;yp,up分别为广义气动力和广义位移[1]。
1.3 状态空间模型
1.3.1 ARMA矩阵和变换
使用Hankel矩阵法将ARMA模型转换得到一个不可约的状态空间表达式[13]。式(4)可以用以下的向量写成矩阵形式:

则:
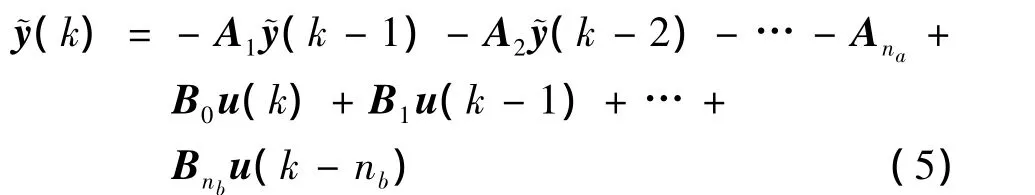
其中:

将式(5)进行z变换可得:

1.3.2 Markov参数表达式
任何的线性动力系统采样数据都可以写成Markov参数表达式的形式。因此,式(6)可以等效写为:
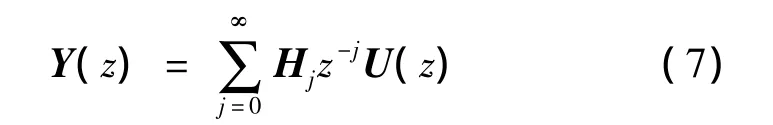
式中:Hj为 Markov 参数,Hj∈RN×N。
由式(6)和式(7)可得[12]:
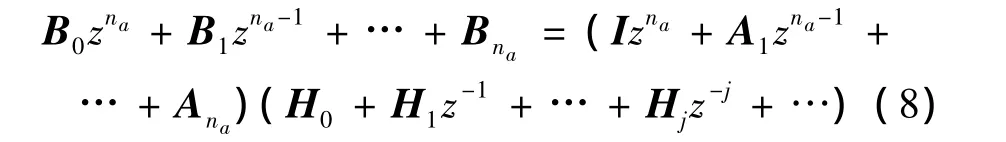
可得Markov参数的计算表达式:
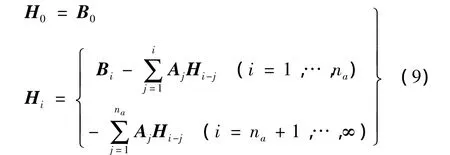
1.3.3 连续时间的状态空间实现
对于ARMA模型和Markov参数模型的状态空间实现并不是唯一的,通过Hankel矩阵得到状态空间的不可约状态[13]:
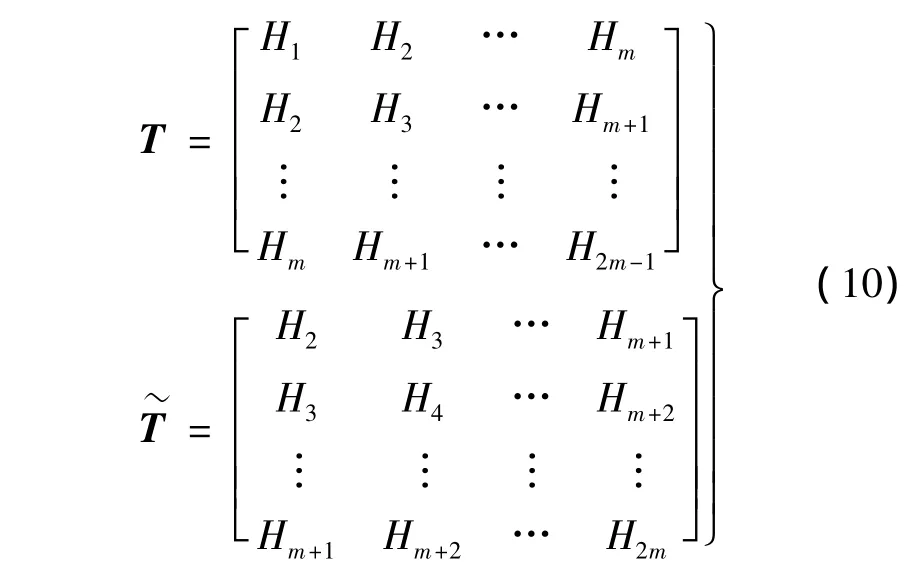
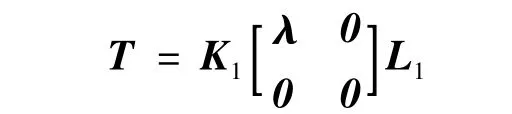
其中:
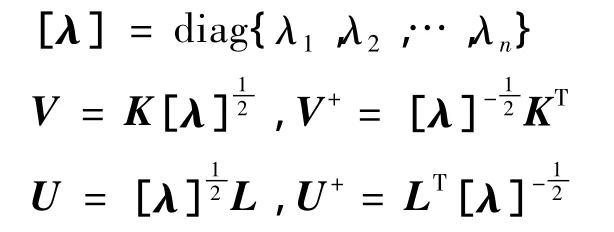
将Hankel矩阵T进行奇异值分解,得到:
据此得到一个不可约的离散状态空间:
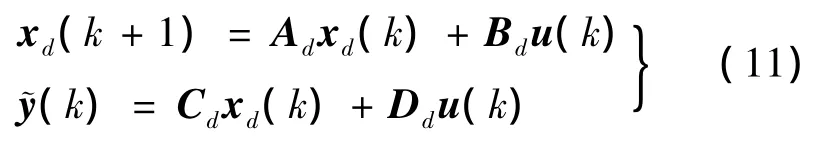
其中,输入和输出的矩阵表达式为:
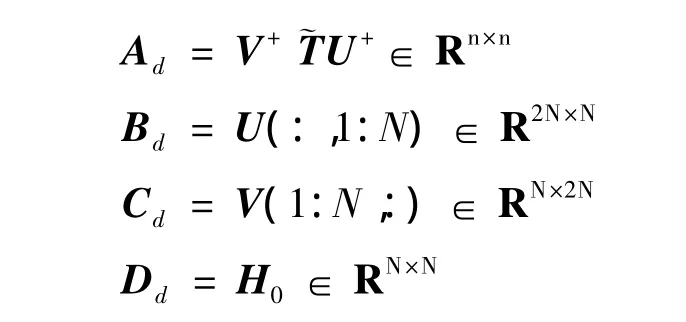
得到气动力对模态位移的响应离散状态空间模型式(11)后,通过Laplace微分算子进行z变换,可以很方便地获得等效的连续时间状态空间模型。

其中,输入输出矩阵表达式为[12]:
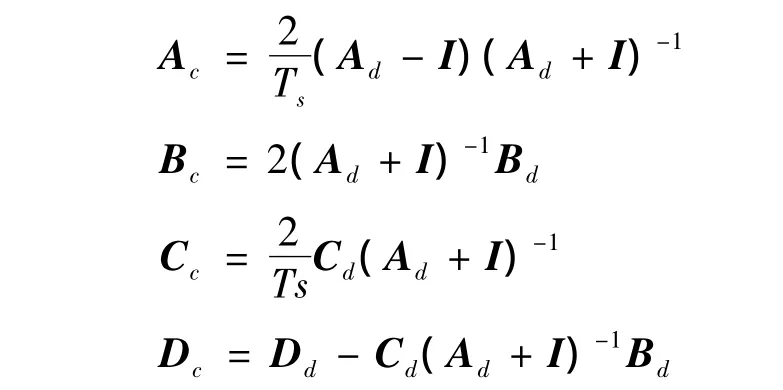
1.4 线性颤振闭环分析
控制方程采用结构动力学方程如下:
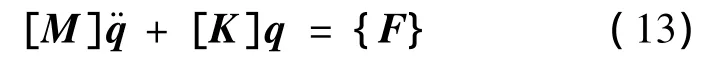
为了便于时域求解式(13)给出的结构动力学方程,引入状态变量,则式(13)可写成状态空间的形式:
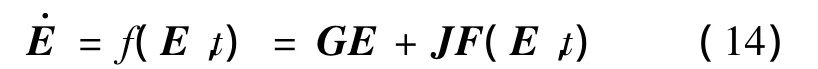
其中:
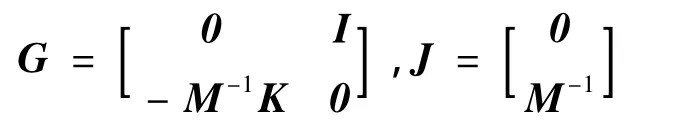
式中:M,K分别为结构广义质量和刚度矩阵;E,F分别为广义坐标向量和广义气动力向量。
使用非定常气动力的状态空间式(12),该ARMA/ROM取代CFD求解器与结构动力学状态空间(14)进行耦合,进行高精度的气动弹性分析,采用四阶龙格-库塔方法求解微分方程组。
2 算例与分析
本文使用AGARD445.6机翼进行了颤振计算。颤振分析主要取其前四阶模态,即一阶弯曲(mode1,9.57 Hz)、一阶扭转(mode2,38.17 Hz)、二阶弯曲(mode3,48.35 Hz)和二阶扭转(mode4,91.55 Hz)。
Euler方程可以较准确地模拟跨声速气动力,对网格和计算资源的要求也相对适中;Euler/BL方法是以Euler方程为控制方程,通过边界层方程计算边界层特性[14-15]求解无粘流场。Euler/BL方程很好地补足了Euler方程无法考虑流体粘性的缺点,不论是定常还是非定常计算都具有很高的精度[14-15]。因此,文中的CFD直接模拟和ROM训练过程均分别使用以Euler和Euler/BL方程为控制方程进行计算和辨识。
分别采用ARMA/ROM和CFD全阶模拟方法对AGARD445.6机翼的颤振特性进行分析,图3给出了Ma=0.901工况的Euler/BL辨识结果。对降阶和全阶计算结果与风洞试验值之间的比较如图4和图5所示。
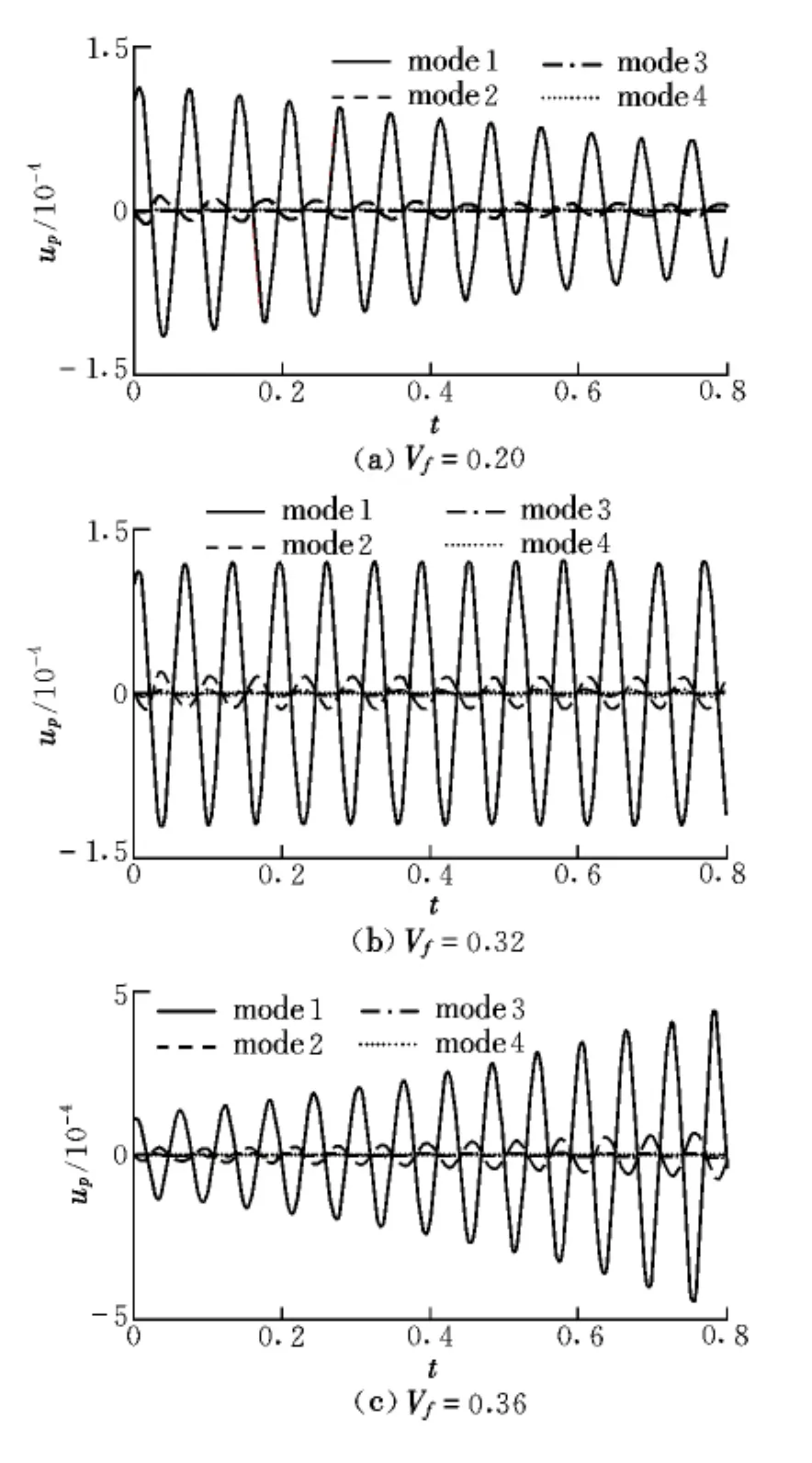
图3 ARMA/ROM辨识结果Fig.3 Identification results of ARMA/ROM
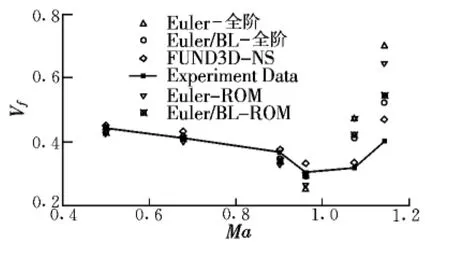
图4 全阶与降阶系统颤振速度比较Fig.4 Comparison for flutter speeds of full-order and reduced-order systems
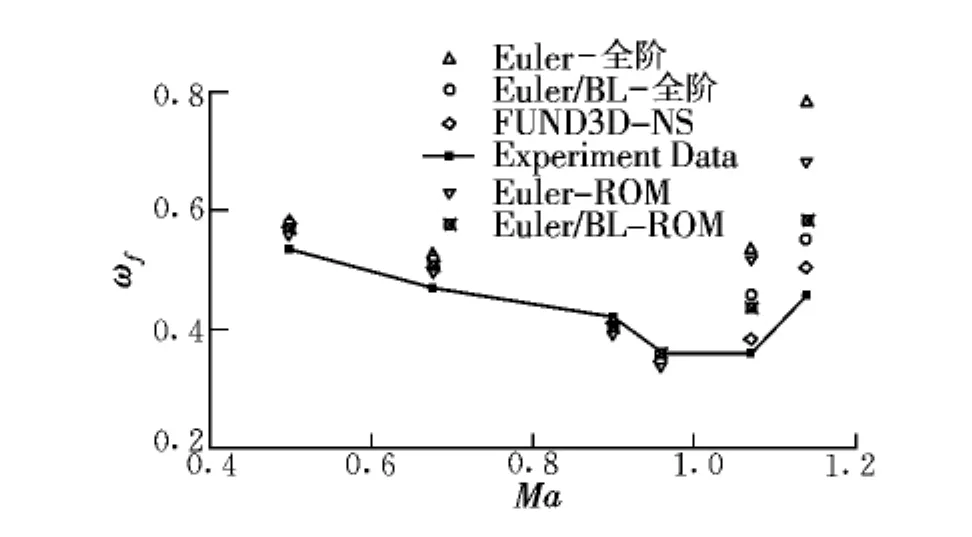
图5 全阶与降阶系统颤振频率比较Fig.5 Comparison for flutter frequencies of full-order and reduced-order systems
对于亚声速、跨声速和超声速三种工况,ARMA/ROM方法所得到的机翼颤振特性和CFD全阶模拟差别均较小。两种方法的精度相当,这也体现了气动力ROM技术在复杂气动弹性问题中的应用潜力。
通过比较全阶气动弹性计算方法和气动力辨识法对AGARD445.6机翼的颤振分析结果,得出如下结论:
(1)两种方法计算结果的趋势一致,AGARD445.6机翼颤振“凹坑点”大约在 Ma=0.954附近;
(2)气动力辨识法和全阶气动弹性的计算结果基本一致,但在计算效率上气动力辨识法能提高3~4倍;
(3)从两种方法与试验值的比较来看,在“凹坑点”之前,本文采用Euler/BL方程辨识计算结果与试验值符合性比N-S方程计算结果更好一些;在“凹坑点”之后N-S方程计算结果更接近于试验结果。总体而言,二者的计算精度相差不大,但Euler/BL方程的辨识计算效率比N-S方程要高,这也正是本文采用Euler/BL方程作为流场控制方程的主因。
3 结束语
本文以状态空间方程的形式提供了一种低维的流体模型,通过ARMA/ROM技术识别流体模态,采用系统实现理论基于Markov参数获得模态系数相对应的状态空间模型。结果表明,基于ARMA的降阶模型能高效准确地模拟全阶气动弹性模型的特征,准确地预测流体系统的动态行为;相对于全阶系统而言,自由度数量以及计算时间都大幅缩减,为下一步进行三维机翼的工程应用计算奠定了基础。
[1] 杨超,刘晓燕,吴志刚.基于POD-Observer技术的非定常气动力建模方法[J].中国科学:技术科学,2010,40(8):861-866.
[2] Hall K C,Thomas JP,Dowell E H.Reduced-order modeling of unsteady small-disturbance flows using afrequencydomain proper orthogonal decomposition technique[R].AIAA-99-0655,1999.
[3] Hall K C,Thomas JP,Dowell E H.Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows[J].AIAA Journal,2000,38(2):1853-1862.
[4] Silva W A,Raveh D E.Development of unsteady aerodynamic state-space models from CFD-based pulse responses[R].AIAA-2001-1213,2001.
[5] 徐敏,李勇,曾宪昂,等.基于Volterra级数的非定常气动力降阶模型[J].强度与环境,2007,34(5):22-28.
[6] 陈刚,徐敏,陈士橹.基于Volterra级数的非线性非定常气动力降阶模型[J].宇航学报,2004,25(5):492-495.
[7] 崔鹏.基于CFD/CSD的机翼气动弹性计算研究[D].南京:南京航空航天大学,2011.
[8] Cowan T J,Arena A S.Development of a discrete-time aerodynamic model for CFD-based aeroelastic analysis[R].AIAA-99-765,1999.
[9] Gupta K K,Voelker L S.CFD-based aeroelastic analysis of the X-43 hypersonic flight vehicle[R].AIAA-2001-0712,2001.
[10]张伟伟,叶正寅.基于气动力降阶模型的跨音速气动弹性稳定性分析[J].计算力学学报,2007,24(6):768-772.
[11] Lai K L,Tsai H M.Flutter simulation and prediction with CFD-based reduced-order model[R].AIAA-2007-731,2007.
[12] Lai K L,Lum K Y.Flutter-boundary prediction using system identification-based reduced-order aeroelasticity analysis[R].AIAA-2012-1710,2012.
[13]刘党辉.系统辨识方法及应用[M].北京:国防工业出版社,2010:90-94.
[14] Gao C,Luo S,Liu F,et al.Calculation of airfoil flutter by an Euler method with approximate boundary conditions[R].AIAA-2003-3830,2003.
[15]马艳峰,贺尔铭,李俊杰,等.大展弦比机翼的静气动弹性研究[J].航空计算技术,2014,44(3):53-57.

