线性离散时滞系统的指数稳定性❋
李云璐, 高存臣
(中国海洋大学数学科学学院,山东 青岛 266100)
线性离散时滞系统的指数稳定性❋
李云璐, 高存臣
(中国海洋大学数学科学学院,山东 青岛 266100)
本文研究了一类线性离散时滞系统的指数稳定问题。通过构造适当的Lyapunov-Krasovskii泛函,利用矩阵不等式技术,给出了线性离散时滞系统与时滞相关的指数稳定的充分条件。应用本文的结果,得到了不确定离散时滞系统与时滞相关的鲁棒指数稳定的新判据,并用数值算例说明了本文结果的可行性与有效性。
时滞相关; 指数稳定; 线性矩阵不等式; 线性离散系统; 时滞
在生物、物理等实际过程的控制系统中都存在着时滞现象,通常时滞会使系统性质变差,例如,会引起系统的震荡、不稳定[1],分析和研究时滞系统的稳定性条件已成为系统控制和设计中很重要的一个课题,因而引起若干学者的广泛关注[2-8]。离散时滞系统的稳定性在理论和实际应用中有着不可替代的位置,然而,相对于对连续时滞系统的稳定性和应用的关注[9-12],人们对离散时滞系统稳定性和应用的研究相对较少[13-17]。而实际中又需要离散时滞系统稳定性,如在生产库存系统中,货物的库存量x(k+1)往往与上个月的库存量x(k)以及前面几个月的库存量x(k-h)有关,还与产量u(k)与销售量S(k)有关,表现在数学模型上就是如下形式的离散时滞系统:
文献[13]研究的是一类不确定离散时滞系统,改进了系统为渐近稳定的充分条件;文献[10,12]研究的是一类带有时滞的线性连续系统的指数稳定性问题,并将结果应用到了不确定线性系统指数稳定的判据上,文献[10]中的时滞在给定的区间内连续,不一定可微,文献[12]中的时滞是个恒定的常数。
基于此,本文将文献[10,12-13]的研究方法有机地结合起来,考虑了一类带有常时滞的线性离散系统的指数稳定问题。通过构造合适的Lyapunov-Krasovskii泛函,利用矩阵不等式技术,给出了该系统与时滞相关的指数稳定的判定条件,同时也得出了不确定离散时滞系统为指数稳定的新判据,在文章最后给出了相应系统的仿真算例。
1 预备知识
考虑如下的线性离散时滞系统
(1)
其中:x(k)∈n是状态向量;A,A1是有适当维数的常数矩阵;n是初始函数序列;范数定义为φ(k);h∈+是系统的常时滞。
定义1.1[9]对于任意给定的常数0<α<1,如果存在常数c>0,使得x(k)≤cφhαk,∀k∈对所有的初始函数序列都成立,那么系统(1)称为α-指数稳定的。
引理1.1[17]对于给定具有适当维数的矩阵Q=QT,E,H,则Q+HFE+(HFE)T<0对所有满足F(t)T·F(t)≤I的矩阵F(t)都成立的充要条件是存在一个正数ε>0使得下式成立
Q+εHHT+ε-1ETE<0。
引理1.2 (Schur补引理)[17]对给定的对称矩阵

(1)S<0;
2 主要结果
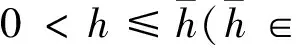
这里,
证明 构造Lyapunov泛函
V(k)=V1(k)+V2(k)+V3(k),
(3)

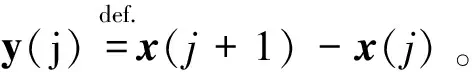
从而有如下关系式成立:
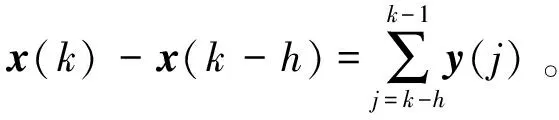
令(3)式沿系统(1)求差分,得
x(k+1)TPx(k+1)-x(k)TPx(k)-
2x(k)TY[x(k)-x(k-h)]+
2x(k-h)TW[x(k)-x(k-h)];
x(k)TQx(k)-α2(h-1)x(k-h)TQx(k-h)+
(1-α-2)V2(k+1)+α-2x(k)TQx(k)-
α2(h-1)x(k-h)TQx(k-h);
(1-α-2)V3(k+1)+hα-2y(k)TRy(k)-
经过整理,可得到
(4)
这里:
Ω1def.=

因此,ΔV(k)-(1-α-2)V(k+1)<0,
从而有
ΔV(k)<(1-α-2)V(k+1)≤0,(0<α<1),
V(k+1)<α2V(k),(0<α<1)∀k∈。
(5)
由(5)式可以推出:
V(k)<α2V(k-1)<…<α2kV(0),
在这里,引入记号
从而有

所以,
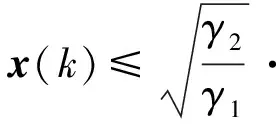
这说明线性离散时滞系统(1)是指数稳定的。证毕。
基于定理3.1,可推出不确定线性离散时滞系统的鲁棒指数稳定性判据。
考虑如下系统:
(6)
这里:A(k)=A+ΔA(k);A1(k)=A1+ΔA1(k);ΔA(k),ΔA1(k)是具有适当维数的不确定参数矩阵,且满足如下形式:
ΔA(k)=DF(k)E1,ΔA1(k)=DF(k)E2,
其中:D,E1,E2是具有适当维数的常数矩阵;F(k)是一个未知的时变矩阵函数,且满足
F(k)T·F(k)≤I,∀k∈。


证明 构造与定理3.1证明中相同的Lyapunov泛函,并把定理3.1中Ω表达式中的A,A1,分别用A+DF(k)E1,A1+DF(k)E2代替,经过整理,得到
(8)
再结合引理1,(8)式成立的充要条件是存在一个正数ε>0,使得下式成立:
(9)
对(9)式利用Schur补引理,即可得到定理3.2中的(7)式成立。证毕。
注 令本文定理3.2中的α=1,可得到系统(6)渐近稳定的判定条件,与文献[13]中的定理1,结论类似。
3 数值例子
例3.1 考虑系统(1),其中



例3.2 考虑系统(6),其中
D=A1;F(k)=diag{sink,sink};E1=E2=I。
令ε=0.5,利用MATLAB中的LMI工具箱可知,当α=0.6时,定理2.2中的线性矩阵不等式(7)是可行的,相应的可行解为




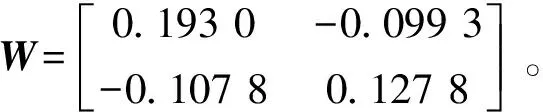
表1 不同的指数稳定度α对应不同的最大的时滞Table 1 Maximum time delays on different exponential decay rates α

指数稳定度①αExponentialdecayratesα最大的时滞②hMaximumtimedelaysh0.6050.6350.6660.6970.7270.7590.78100.81120.84150.87180.9025
4 结语
本文主要研究了一类带有常时滞的线性离散系统的指数稳定问题。通过构造合适的Lyapunov-Krasovskii泛函,利用矩阵不等式技术,给出了上述系统与时滞相关的指数稳定的判定准则,然后将本文的结论应用到了不确定离散时滞系统,得出了不确定离散时滞系统为指数稳定的新判据。最后,用2个数值算例说明了本文结果的可行性与有效性。
利用本文的方法,还可以研究带有变时滞的线性离散系统的指数稳定性问题,限于篇幅,在这里就不赘述了。
[1] Hale J K, Verduyn Lunel S M. Introduction to functional differential equations[M]. New York : Springer-Verlag, 1993.
[2] Niculescu S I. Delay effects on stability: A robust control approach [M]. Lecture Notes in Control and Information Sciences, London: Springer-Verlag, 2001.
[3] Gu K, Kharitonov V L, Chen J. Stability of time delay systems [M]. Boston: Brikhauser, 2003.
[4] Han Q L. A descriptor system approach to robust stability of uncertain neutral systems with discrete and distributed delays [J]. Automatica, 2004, 40: 1791-1796.
[5] He Y, Wu M, She J H, et al. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays [J]. System and Control Letters, 2004, 51: 57-65.
[6] Jiang X, Han Q L. OnH∞controlforlinearsystemswithintervaltime-varingdelay[J].Automatic, 2005, 41: 2099-2106.
[7]XuS,LamJ.Improveddelay-dependentstabilitycriteriafortime-delaysystems[J].IEEETransactionsonAutomaticControl, 2005, 50: 384-387.
[8]HeY,WangQG,XieL,etal.Furtherimprovementoffree-weightingmatricestechniqueforsystemswithtime-varyingdelay[J].IEEETransactionsonAutomaticControl, 2007, 52: 293-299.
[9]ZhuS,LiZ,ZhangC.Exponentialstabilityanalysisforpositivesystemswithdelays[J].IETControlTheoryApplication, 2012, 6(6): 761-767.
[10]PhatVN,KhongthamY,RatchagitK.LMIapproachtoexponentialstabilityoflinearsystemswithintervaltime-varyingdelays[J].LinearAlgebraanditsApplications, 2012, 436: 243-251.
[11]KharitonovV,MondieS,ColladoJ.Exponentialestimatesforneutraltimedelaysystems:anLMIapproach[J].IEEETransactionsonAutomaticControl, 2005, 50(5): 666-670.
[12]CaoJW.Improveddelay-dependentexponentialstabilitycriteriafortime-delaysystem[J].JournaloftheFranklinInstitute, 2013, 350: 790-801.
[13]XuSY,LamJ,ZouY.Improvedconditionsfordelay-dependentrobuststabilityandstabilizationofuncertaindiscretetime-delaysystems[J].AsianJournalofControl, 2005, 7(3): 344-348.
[14]ZhangY.Robustexponentialstabilityofdiscrete-timedelayimpulsivesystemswithparametricuncertainties[J].AsianJournalofControl, 2013, 15(1): 310-315.
[15]GaoH,ChenT.Newresultsonstabilityofdiscrete-timesystemswithtime-varyingstatedelay[J].IEEETransactionsonAutomaticControl, 2005, 78: 235-246.
[16]PhanTN.Exponentialstabilitycriterionfortime-delaysystemswithnonlinearuncertainties[J].AppliedMathematicsandComputation, 2009, 214: 374-380.
[17]TangXM,YuJS.Stabilityanalysisofdiscrete-timesystemswithadditivetime-varyingdelays[J].InternationalJournalofAutomationandComputing, 2010, 7(2): 219-223.
责任编辑 陈呈超
Exponential Stability of Linear Discrete Time Systems with Delays
LI Yun-Lu, GAO Cun-Chen
(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China)
This paper investigates the exponential stability problem for a class of linear discrete-time systems with time delays. Firstly, by constructing appropriate Lyapunov-Krasovskii functional and linear matrix inequalities (LMIs) technique, a delay-dependent sufficient condition of exponential stability is derived for the linear discrete-time systems with time delays. Secondly, the result is applied to uncertain discrete time delay systems and a new criterion of the robust exponential stability is also proposed.Lastly, numerical example is given to show the effectiveness and feasibility of the obtained result.
delay-dependent; exponential stability; linear matrix inequalities (LMIs); linear discrete-time system; time delay
国家自然科学基金项目(60974032)资助
2013-09-28;
2014-05-30
李云璐(1990-),女,硕士生。E-mail:qufuliyunlu90@163.com
TP13
A
1672-5174(2015)09-136-05
10.16441/j.cnki.hdxb.20130367

