一种永磁电机空载气隙磁场解析计算方法*

潘元璋 赵龙龙

(91388部队93分队 湛江 524000)



一种永磁电机空载气隙磁场解析计算方法*

潘元璋 赵龙龙

(91388部队93分队 湛江 524000)

论文以气隙中一对载流线圈产生的磁场为基础,利用等效面电流法推导出了平行充磁永磁电机空载时的气隙磁密的解析计算公式。在考虑定子开槽的情况下,利用许-克变换构造了气隙相对比磁导函数,给出了定子开槽时空载气隙磁密分布的解析计算方法。并对比了永磁电机气隙磁场的解析计算结果与二维有限元法的计算结果,对比结果显示两者的波形和大小吻合很好,证明了解析计算方法是准确可靠的,同时,解析据算法在计算机上容易实现,该方法为永磁电机的优化设计和性能分析提供了基本的分析手段。

永磁电机; 气隙磁场; 面电流法; 解析计算

Class Number TM341

1 引言

永磁电机相对传统感应电机,以其结构简单、重量体积小、效率高、振动噪声低等优点,得到了越来越广泛的应用,特别是随着舰艇,UUV、鱼雷等水下武器装备的迅猛发展,对电机的振动噪声和功质比(功率质量比)等方面提出了非常苛刻的要求,而永磁电机所表现出来的明显优势必将成为电机行业的佼佼者。准确的计算永磁电机气隙内的磁场分布是对其进行优化设计以及性能分析工作的先决条件,国内外许多学者对永磁电机,特别是对磁场分布计算的各种方法进行了较深的研究[1～5]。

有限元数值计算方法可以准确计算出电机气隙磁场的分布,具有通用性强、适用媒质多样的特点[6]。但因其对使用者有较高的专业技术要求且前处理过程繁杂、计算时间偏长而不易采用。解析计算法能够较为准确地计算电机气隙磁场分布的同时又可以直观反映电机气隙磁场分布与其本体结构尺寸之间的关系[7～8],故该方法的工程实用价值较大。本文以表面贴磁式永磁电机为研究对象,首先考虑定子无槽情况下,推导得出其气隙磁场的解析计算公式;而后考虑定子开槽情况,构造气隙相对比磁导函数来拟合因开槽对气隙磁场的影响;最后用二维有限元法验证了解析方法是正确可靠的。为永磁电机的优化设计和性能分析提供了基本的分析手段。

2 定子表面光滑时气隙磁场计算

考虑垂直于电机轴的平行平面场,此时电流密度以及矢量磁位只在z轴方向有分量。稳态情况下,平面场域Ω上的电磁场问题就转化到了二维空间,可以用直角坐标系描述,其矢量磁位满足泊松方程[9～10]:

(1)

式中μ0=1/ν为磁导率(ν为磁阻率),Az为z轴方向的矢量磁位,J(x,y)为源电流密度,Ht为磁场强度的切向分量,S1为第一类边界条件,S2为第二类边界条件。

2.1 气隙中一对载流线圈的磁场

假设电机铁磁材料的磁导率μFe=∞,一对线圈放置在气隙中,由两条有效边A和B组成,如图1所示,把每条边产生的矢量磁位叠加,即可得出整个线圈在电机气隙中所产生的磁场[5]。

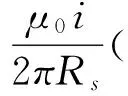
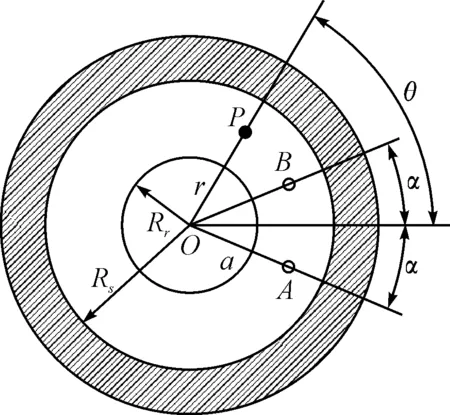
图1 气隙中一对载流线圈

在载流线圈以外的区域有J(r,θ)=0,考虑边界条件求解方程(1)可得到电机气隙中一对载流线圈在气隙中任一点P(r,θ)的矢量磁位为

(2)

通常在表面贴磁式永磁电机中,定子侧开有若干槽,线圈作为绕组放置在槽内,经过修正可近似认为绕组嵌放在定子内表面上(即径向距离r=Rs),由此可推导出一对载流线圈在定子内表面处的径向磁密为

(3)

式中,Kym=sinmα为m次谐波的节距因数。

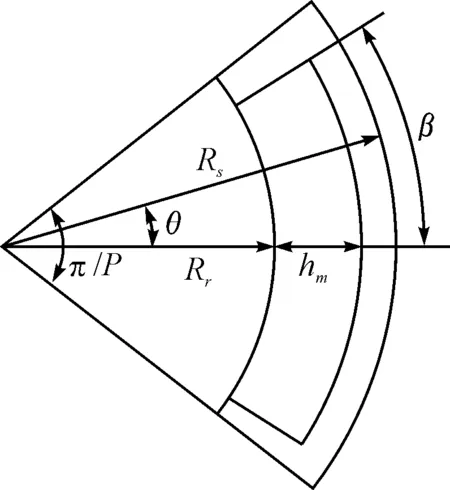
图2 瓦片结构永磁体一个磁极的结构

2.2 多极永磁体产生的气隙磁场

在表面贴磁式永磁电机中,永磁体通常采用瓦片形磁极结构,其结构如图2所示,P为永磁体的极对数,2β为一块永磁体的张角,hm为永磁体厚度,Rs为电机定子内半径,Rr为电机转子外半径。

瓦片形磁极有平行和径向两种充磁方式,考虑到平行充磁方式永磁体制作工艺简单,容易实现,且应用广泛,而径向充磁方式工艺上难以达到,因此分析平行充磁永磁体产生的气隙磁场更有代表性和实用性。

永磁体平行充磁是指其磁化方向和瓦片形永磁体的中心线相平行,其磁化方向和永磁体等效面电流等效如图3所示。

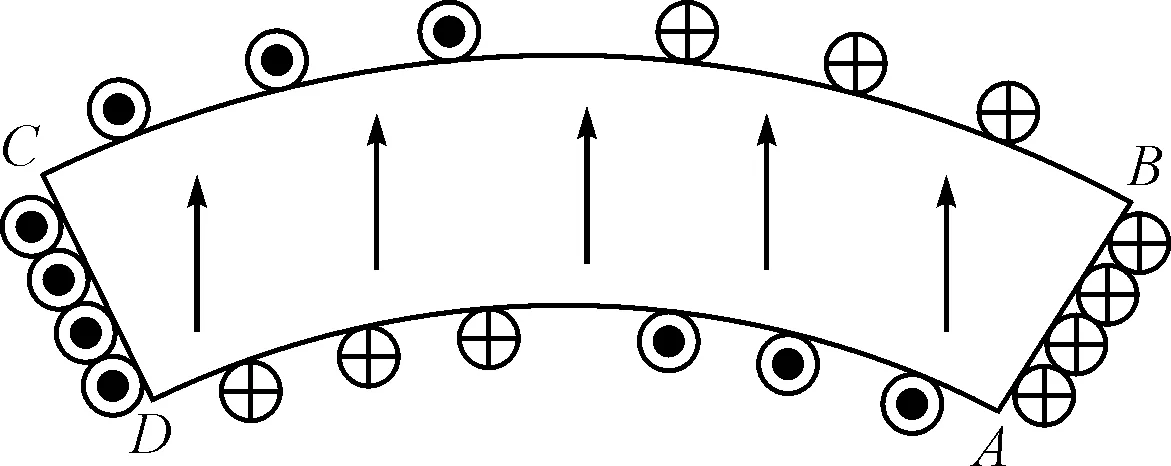
图3 平行充磁时的永磁体面电流等效

由永磁体的等效面电流法可知,永磁体AB面与CD面的等效面电流大小相同但方向相反,电流密度大小可表示为

J1=Hccosβ

(4)

同样的,沿AD和BC面面电流密度可表示为

J2=Hccosξ

(5)

式中ξ为AD或BC上任意一点与永磁体中心线的机械夹角。

考虑同心瓦片形永磁体平行充磁时AB_CD段等效面电流在电机气隙中产生的磁场可表示为

(6)

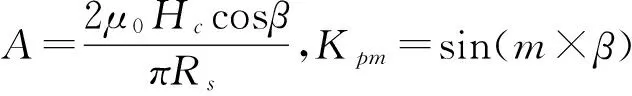
BC段等效面电流产生的气隙磁密可表示为

(7)

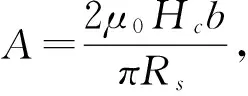
在Cm中,b=Rr+hm;

AD段面电流产生的气隙磁密可表示为

(8)

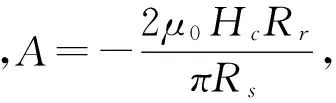
由以上推导可得出单块永磁体在电机定子内表面产生的磁密B1(θ)可视为AB、CD、BC和AD各段的叠加,即:

B1(θ)=BAB_CD1(θ)+BBC1(θ)+BAD1(θ)

(9)

同理可以推导得出平行充磁时2P极永磁体的AB、CD、AD、BC各段在电机定子内表面产生的磁密为

BAB_CD2P(θ)=

(10)

式(10)中A、Cm、Kpm和式(6)相同。

(11)

式(11)中A、Cm和式(7)相同。

BAD2P(θ)=

(12)

式(12)中A、Cm和式(8)相同。

于是多极(2p,p>1)瓦片形平行充磁永磁体在电机定子内表面产生的磁密可表示为

B2P(θ)=BAB_CD2P(θ)+BBC2P(θ)+BAD2P(θ)

(13)

3 定子开槽时电机的气隙磁场计算

通常在永磁电机中,定子铁心内表面开有若干放置绕组的槽,转子铁心外表面可视为光滑。对于定子开槽的电机,若其槽口宽度与槽距比较小,在分析气隙中一个槽距内的气隙磁导变化时,其相邻槽对其的影响可忽略不计,反之则不能忽略[5,10]。本文只讨论定子开槽的槽口宽度与槽距比较小的情况,因而可采用图4所示转子铁心表面光滑、定子铁心单个槽时的物理模型进行分析。为简化分析作如下假设[11]:

1) 电机定子铁心单面开槽,转子无槽(光滑);

2) 定子开槽的槽深认为是无限深;

3) 电机铁磁材料的磁导率μFe=∞,定子表面、转子表面均为等标量磁位面,分别为0和Ω0;

4) 电机中永磁体材料退磁曲线认为是线性;

5) 贴于电机转子表面的永磁体间的填充材料认为与永磁体有相同的磁导率。

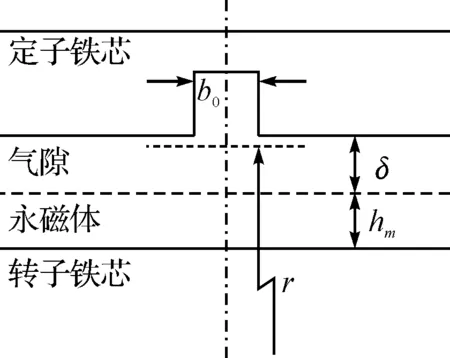
图4 定子侧开槽转子光滑的物理模型

由假设条件可知电机定、转子铁心表面的标量磁位差为Ω0,则利用许-克变换法可以得到永磁电机中气隙、永磁体以及定子槽内区域任意点的磁密值B,该方法可以求解诸多复杂的磁场问题[5]。

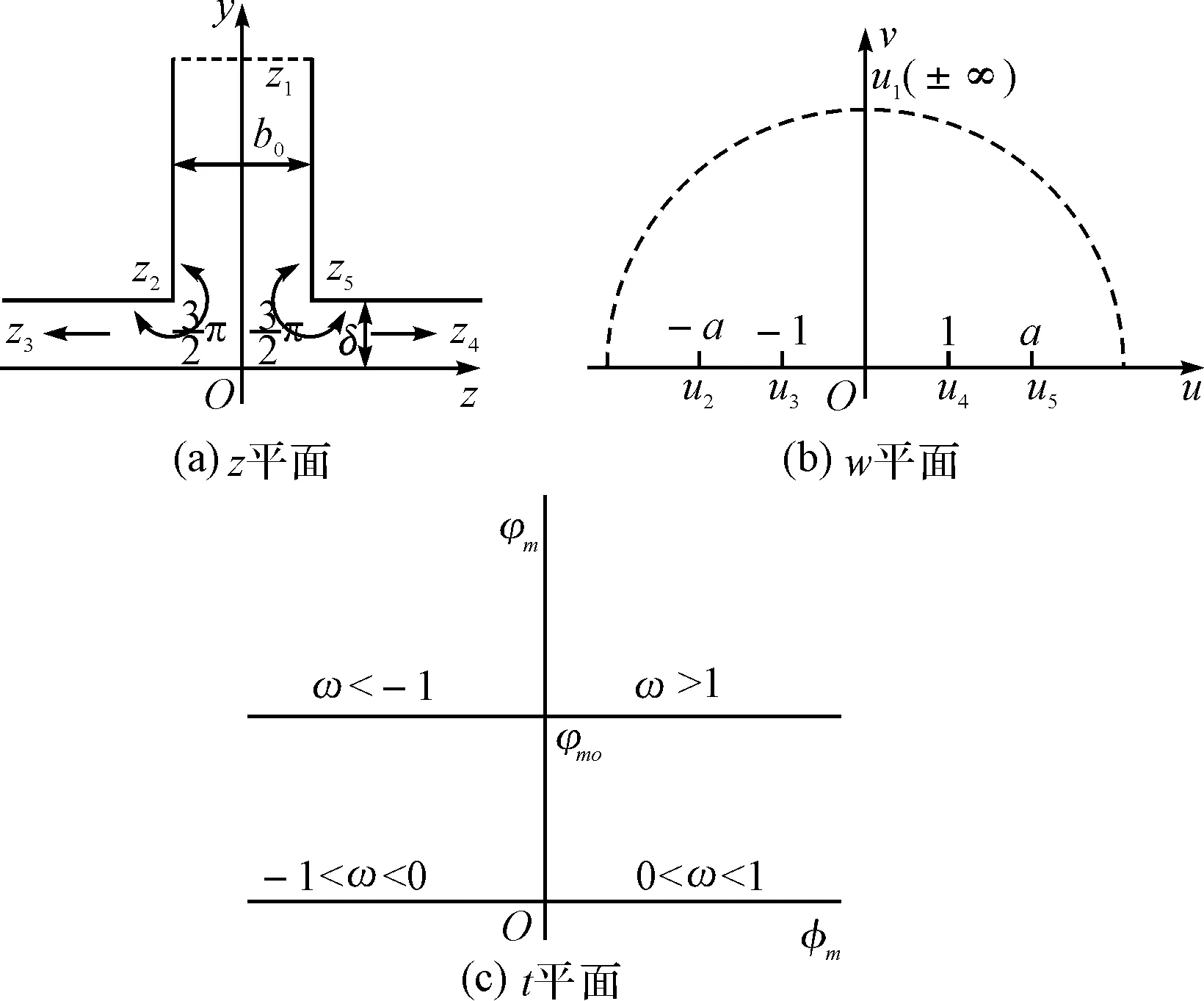
图5 电机定子单面开槽时气隙磁场的变换

考虑多边形的边界面具有两个不同的磁位值的情况,此时通常需要进行两次变换,如图5所示,第一次变换将z平面上的多边形区域和边界变换为ω平面上的上半平面(包括横轴),第二次变换是把ω平面上的映射变换到t平面上,进而即可得到都是直线的等φm线和等φm线。

图5(a)中z平面上原点o到z4点之间的线段代表的是平滑表面的一半,在这半段上面,文献[5]中给出了该平滑面上的磁密函数:

(14)

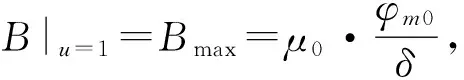
综合以上的分析,对于定子侧单面开槽结构的永磁电机,其气隙磁密B的曲线可以通过如下方法绘制来绘制:以定子无槽时的电机气隙磁密为基值,在电机定子开槽处所减少的磁密值可由式(15)所构建的气隙相对比磁导函数拟合得到。忽略定子侧开槽引起的齿槽效应影响,则整个永磁电机的气隙比磁导分布为周期为τ的周期函数,表示为λ。

(15)

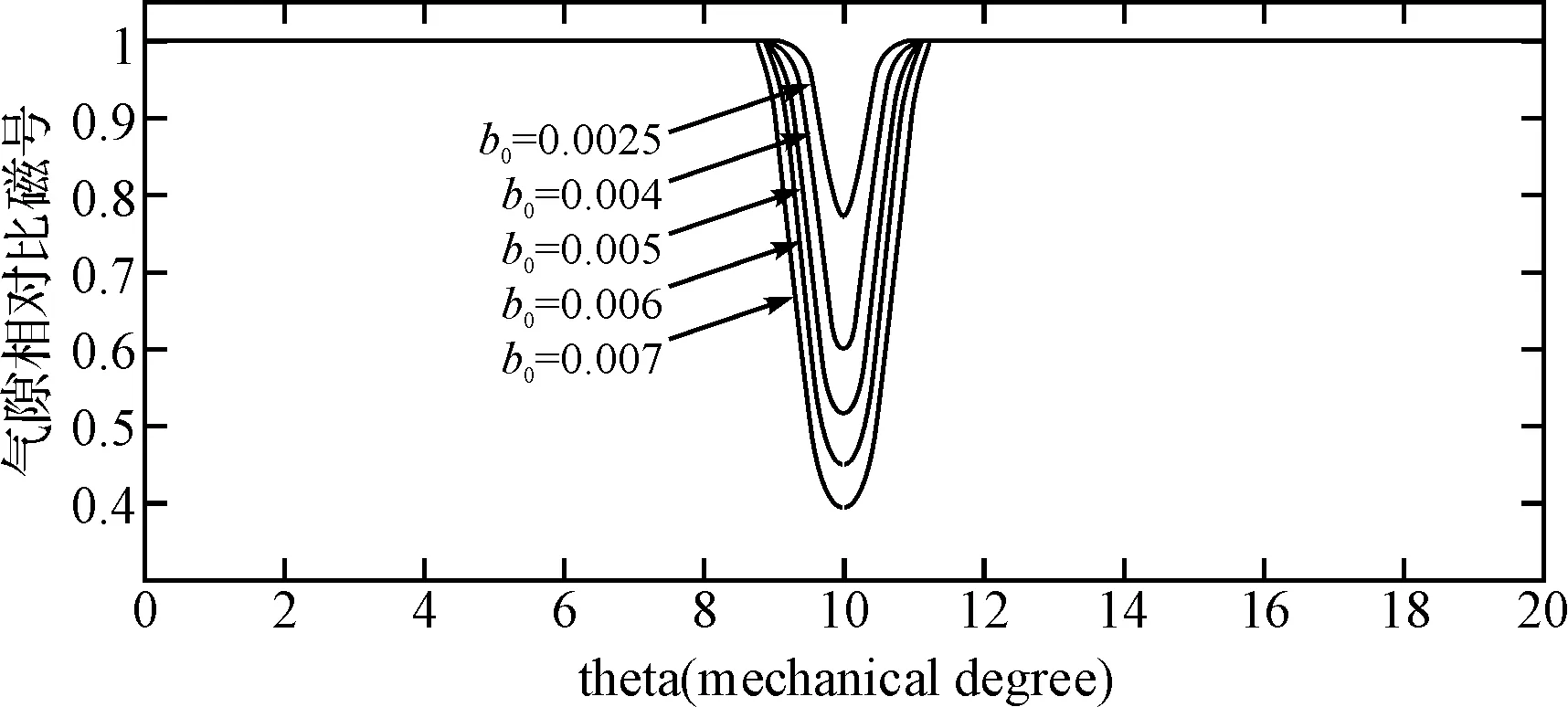
图6 b0变化对气隙相对比磁导的影响

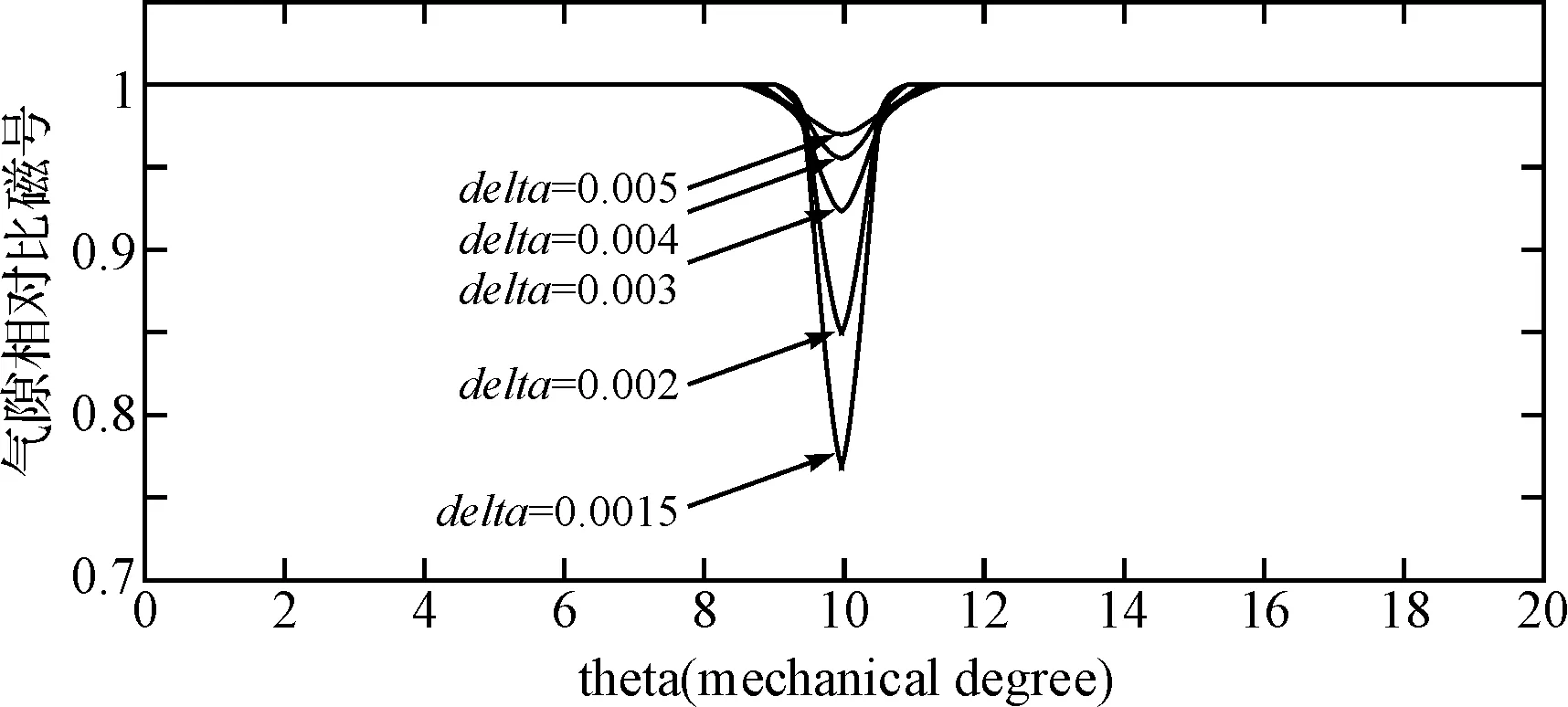
图7 δ变化对气隙相对比磁导的影响

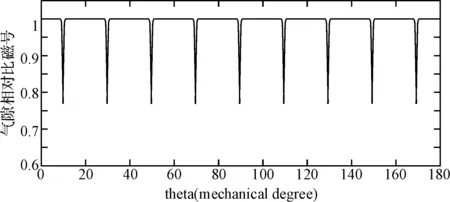
图8 气隙相对比磁导

从上图中,不难看到,在槽中心线处出现气隙相对比磁导的最小值,随齿槽开槽宽度的增加,变化幅度变大;随电机气隙长度的增加,变化幅度减小。图8为一台2极18槽永磁同步电动机定子侧单面开槽时,结合和许-克变换得到的一个极下气隙相对比磁导波形图。

4 解析法和有限元法计算结果比较分析

为了验证本文中计算模型的有效性,利用上述计算方法,对一台2极18槽永磁同步电动机的空载气隙磁场进行了解析计算,该电机相关参数为:转子外半径Rr=28mm,极对数P=1,永磁体厚度hm=6.5mm,永磁体张角2α=180°,矫顽力Hc=935000A/m,定子内半径Rs=36mm,槽距τ=12.56mm,槽口宽b0=2.5mm。同时利用二维有限元对其进行计算,两者结果比对如图9所示。

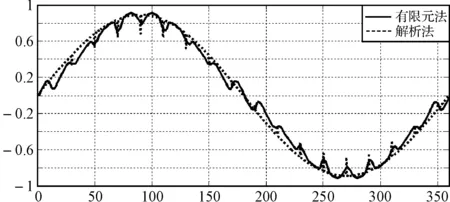
图9 永磁同步电动机的气隙磁场分布

图9中气隙磁密分布波形中含有较大的齿波纹,波形上凸处对应定子齿的位置,波形下凹处对应定子槽的位置。从图中的曲线可看出解析法计算出的磁密波形和有限元法的磁密波形基本吻合,可以满足一般性的工程要求,证明了本文提出的解析计算方法是准确的、可靠的。

5 结语

本文基于面电流法推导了表面贴磁式平行充磁永磁电机定子无槽时气隙磁场的解析计算公式;并结合许-克变换提出了考虑定子开槽情况下永磁电机气隙磁场的解析计算方法,该方法可以简捷快速地求解出永磁电机空载气隙磁场的分布波形;同时利用二维有限元的数值结果证明了该解析计算方法的正确性和可靠性。该解析算法可为永磁电机的优化设计和性能分析提供可靠的手段。

[1] Boules N. Prediction of no-load flux density distribution in PM machines[J]. IEEE Trans. On Industrial Application,1985,21(4):IA-21:633-643.

[2] Zhu Z Q, Howe D. Instantaneous magnetic field distribution in brushless permanent magnet dc motors, Part Ⅰ: Open-circuit field[J]. IEEE Transactions on Magnetics,1993,29(1):124-135.

[3] Seok-Myeong Jang, Kyoung-Jin Ko. Electromechanical Parameters Calculation of Permanent Magnet Synchronous Motor Using the Transfer Relations Theorem[J]. IEEE Transactions on Magnetics,2007,43(6):2495-2497.

[4] 陈阳生,林友仰.永磁电机气隙磁密的分析计算[J].中国电机工程学报,1994,14(5):17-26.

[5] 胡之光.电机电磁场的分析与计算[M].北京:机械工业出版社,1989:10-27.

[6] 田天,李槐树,赖延辉.多相式大气隙无刷直流电机气隙磁场的计算[J].舰船电子工程,2007,27(5):155-158.

[7] 王兴华,励庆孚,王曙鸿.永磁无刷直流电机负载磁场及其电磁转矩的计算[J].中国电机工程学报,2003,23(4):140-144.

[8] Z. Q. Zhu, D. Howe, C. C. Chan. Improved analytical model for predicting the magnetic field distribution in brushless permanent magnet machines[J]. IEEE Trans. Magn,2002,38(1):229-238.

[9] 唐任远,等.现代永磁电机理论与设计[M].北京:机械工业出版社,2006:3-230.

[10] 汤蕴璆.电机内的电磁场[M].北京:科学出版社,1981:57-71.

[11] 王兴华,励庆孚,王曙鸿.永磁无刷直流电机空载气隙磁场和绕组反电势的解析计算[J].中国电机工程学报,2003,23(3):126-131.

An Analytical Calculation Method of No-load Air-Gap Magnetic Field of Permanent Magnet Motor

PAN Yuanzhang ZHAO Longlong

(Unit 93, No. 91388 Troops of PLA, Zhanjiang 524000)

Based on the magnetic field which is produced by a pair of windings on the air-gap, the calculating formulas of the unloaded air-gap flux density generated by parallel-magnetized permanent magnet are conducted with surface current method. Considering the slots in stator core,based on the method of the Schwarz-Christoffel transformation, this paper presents an air-gap relative specific permeance function, calculating the results of no-load air-gap magnetic field when take slots in stator core into account. Compared with the result derived from the 2D finite element method, the analytical method proposed is confirmed, at the same time, the analytical method is much easier achieved through computer. The presented work may act as a basic tool for optimizing design and performance analysis of permanent magnet motors.

permanent magnet motor, air-gap magnetic field, surface current method, analytical calculation

2014年10月9日,

2014年11月24日

潘元璋,男,硕士研究生,助理工程师,研究方向:水下靶标技术。赵龙龙,男,硕士,高级工程师,研究方向:水下靶标技术。

TM341

10.3969/j.issn1672-9730.2015.04.044