基于METRIC模型对可用度与费用关系曲线的研究*

刘剑超 姜 鹏 韩宝玉 郭少臣 张 威

(1.海军航空兵学院 葫芦岛 125001)(2.海军92367部队 青岛 266041)



基于METRIC模型对可用度与费用关系曲线的研究*

刘剑超1姜 鹏1韩宝玉1郭少臣2张 威1

(1.海军航空兵学院 葫芦岛 125001)(2.海军92367部队 青岛 266041)

通过对可修备件管理多级法的分析研究,提出基于优化可修航空器材备件计划库存的方法,针对装备上的各项备件计算各个航空部门的最优库存量,航空备件需求量和其他参数,以此来寻求仓库短缺数最低,相当于寻求装备可用度最高。最终以可用度与费用最优关系曲线的形式推荐给航空部门备件主管人员。

库存量; METRIC模型; 期望短缺数

Class Number TP391

1 引言

库存不是目的,只是储备的一个信息,至于库存是否真正成功,则要看库存为客户或自身创造了多大的经济效益,带来了哪些深刻的影响。

1966年,美国德兰公司著名备件管理专家克雷格C.舍布鲁克博士曾为美国空军提出可修复备件管理多级法(METRIC模型)。众所周知,在航空领域中,航空备件价格一般较高,需求量却比较低。所以,对于具体的航空备件来说,很少见到大量的基地级修理,同时,也很少向仓库提出成批量的申请补给。从事这类航空备件库存问题研究时可运用METRIC模型[1～2]。

库存管理的目的是要确定各项备件的可用度与费用的最优关系。可以将其认为是要采购的初始供应规划各项备件的总件数。在航空备件的保障过程中有两项重要指标:满足率,短缺数。所谓短缺数是指某一时间未满足供应的航空备件需求数。短缺数衡量的是任一时机尚未满足需求的次数,我们主要关心的是上述指标的期望值,也就是期望短缺数。

2 最优短缺数的推导过程

建立METRIC的原理分为两步。第一步是如何构建单项航空备件的费用-短缺数最优曲线。第二步是利用边际分析法将各项航空备件综合为一种航空装备系统进行优化。转换成航空装备可用度-费用最优曲线[3]。

首先对单项航空备件进行定义:Mi为第i个航空部门月平均需求量;Ti为第i个航空部门以月为时间单位的平均修理时间;Ni为第i个航空部门供应渠道平均件数;Ri为第i个航空部门修理航材备件的概率;Oi为航空备件总仓库与第i个航空部门之间从申请(订货)至交货的平均时间。

正数下标表示不同基地的编号,下标0表示航空备件总仓库。航空部门航空备件的供应渠道由两部分待收航材备件组成:修复返回航空备件的件数,航空备件总仓库补给的件数[4]。

申请(订货)至交货时间的定义是从航空部门发出补给申请(订货),到收到航空备件总仓库发来的备件为止这一段时间,前提条件是航空备件总仓库收到补给申请且有库存。

而航空备件总仓库收到补给申请时并不是总是相对应的航材备件,这时就会出现延误。METRIC模型中航空备件总仓库的延误时间,取决于自身的库存量。然后就可以计算各个航空部门的航空备件短缺量,该短缺量取决于航空备件总仓库补给的延误时间和库存量。

必须计算后方仓库的平均需求量,对i个航空部门不能修理的航空备件求和:

(1)

在假设过程中,航空备件需求服从泊松分布,数学理论中“泊松过程之和也是泊松过程”的依据成立。航空备件总仓库供应渠道平均值是M0T0,后方仓库期望短缺数EBO(S0/M0T0)是某一随机时机航空部门补给申请数超过航空备件总仓库的平均量[5～6]。

第i个航空部门每项航空备件需求的供应渠道平均数为

Ni=Mi{RiTi+(1-Ri)[Oi+EBO[S0/M0T0]/M0]}

(2)

假设某航空公司现有五个相同的航空部门,对航空备件的需求均服从泊松分布,且所有i≥1有下列参数可供参考:

Mi=24.3件/年;Ti=0.01年;Ri=0.2;Oi=0.01年;T0=0.024年。

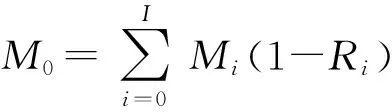
由此可以计算期望短缺数EBO(S)和表1中的一阶差分EBO(S-1)-EBO(S),任一航空部门库存量0～2时的短缺数如表1所示。

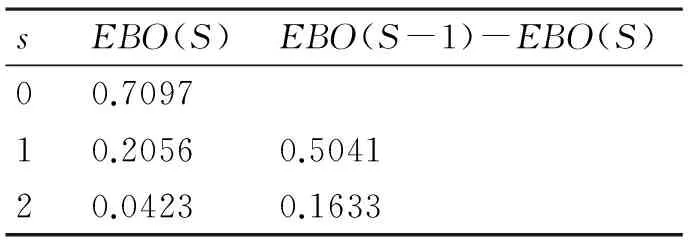
表1 任一航空部门的期望短缺数(后方仓库库存量等于0)

运用边际分析无库存的期望短缺数正好是各个航空部门无库存时的期望短缺数之和(5×0.7097=3.5485)。然后各个航空部门库存量相继增加到1,依次类推。在航空备件总仓库库存量为0的假设条件下,在优化分配库存量过程中,依照上述方式,计算各自的期望短缺数如表2所示。

表2 航空备件总仓库库存量为0时的最优期望短缺数

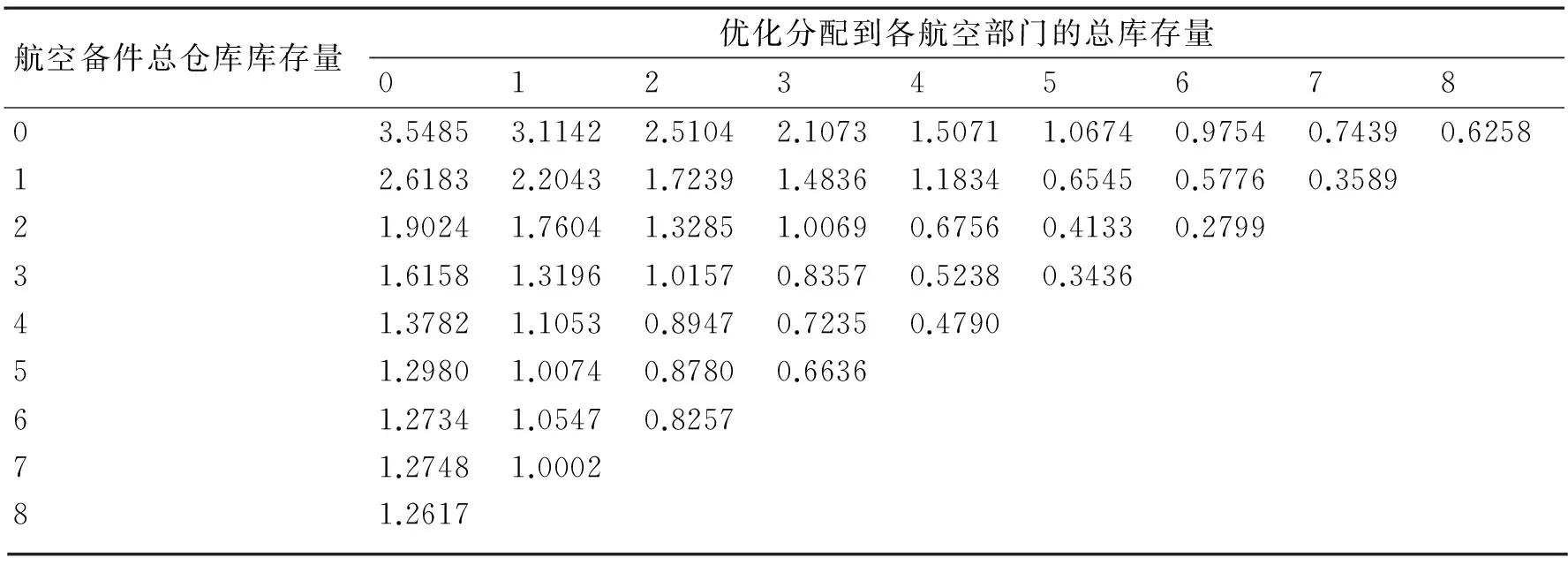
表3 航空备件总仓库任一库存量时航空部门最优期望短缺数

然后,在后方仓库库存航空备件为1时,按照上面的方法步骤,计算新的供应渠道和期望短缺数。运用边际分析法进行排列得出表3。

我们的目的是要计算航空备件总仓库与各个航空部门的库存量最优分配方案。表3的各项数据是指航空备件总仓库指定库存量并据此优化方法分配到各航空部门时的期望短缺数,因此就必须按照从右上方到左上方的对角线取最低短缺数。具体每条对角线上的各个短缺值对应同一个总库存量,该航空备件总仓库库存量在各个航空部门之间进行优化分配[7]。如在表3中,总库存量为2时,对应航空备件总仓库库存量为0,1,2的最优短缺数分别为2.5104,1.9024,2.2043。由于1.9024是最小值,所以将其计入表4。

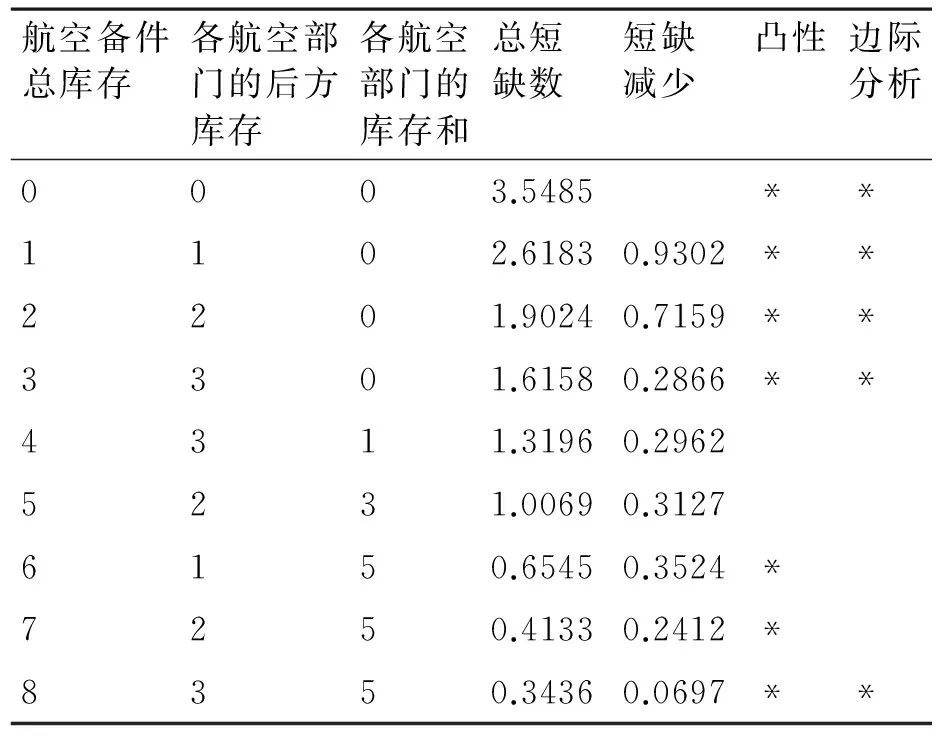
表4 最优期望短缺数

3 关系曲线转化过程

结合上述最优期望短缺数和航空备件的市场价格,先以航空装备备件短缺数与费用的关系曲线形式展现给大家,并通过转化最终以可用度与费用最优关系曲线的形式绘制曲线图,推荐给航空部门备件主管人员[8]。

投资费用按20000元计算,经过反复计算,航空装备备件短缺数与费用关系如图1所示。

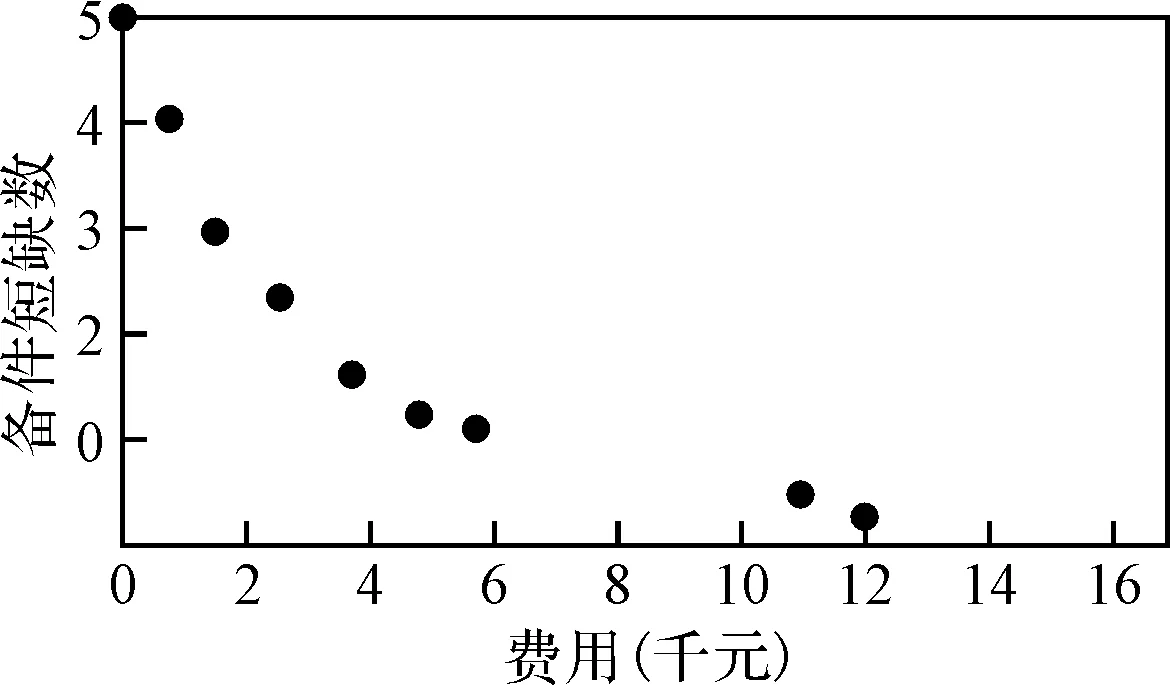
图1 航空装备备件短缺数与费用关系曲线

可用度A是航班中未因任何航空备件短缺而停飞的航班架数所占百分比的期望值,公式如下:

(3)

其中Zi为第i项航空修理部门在一架航班上安装航空器材的数量,N是航班的飞机架数,EBO为期望短缺数[9～10]。

图2的可用度与费用的关系曲线,是将期望短缺数带入式(3)而得出的。

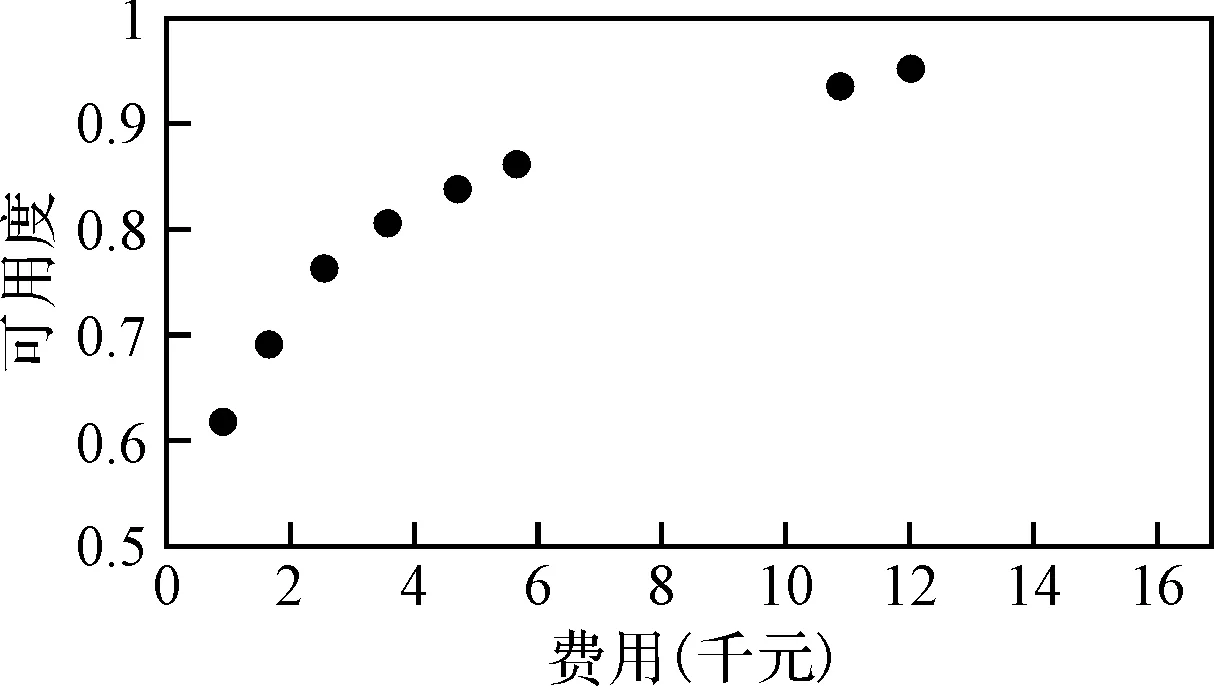
图2 航空装备可用度与费用最优关系曲线

图2所示可用度与费用最优关系曲线中的各离散点,是在规定费用条件下的最高可用度,与该可用度下的最低费用意义相同。

4 结语

利用METRIC模型可针对航空装备上的各项航空备件来计算储备库房库存数、各部门航空备件需求量和其他参数。模型的总目标是所有储备航空备件的仓库中的备件短缺数总和,运用系统的分析方法,以寻求可用度与费用的关系曲线。

[1] [美]Craig C. Sherbrooke.装备备件最优库存建模—多级技术[M].北京:电子工业出版社,2008.

[2] 周曙光,田征.多级库存控制策略的分析[J].大连海事大学学报,2003,45(10):33-35.

[3] 杨平律,包磊.基于METRIC的备件库存优化模型[J].舰船电子工程,2010,198(12):161-164.

[4] 孔翠萍,孟君,杨洁.基于METRIC模型的航材备件管理研究[J].中国电子商务,2010.

[5] 王立超,杨懿,于永利,等.基于系统可用度的匹配问题的分析[J].系统工程学报,2009,134(23):110-114.

[6] 王乃超,康锐.多约束条件下备件库存优化模型及分解算法[J].兵工学报,2009,18(2):23-25.

[7] 蒋庆喜.基于可用度确定MSI维修间隔期的研究[J].航空维修工程,2013.

[8] 杨继坤,徐廷学,董琪,等.基于时间序列分析的装备可用度预测方法[J].海军航空工程学报,2013,34(3):85-89.

[9] 詹克军,赵宁.Ad Hoc网络中Metric优化技术[J].指挥信息系统与技术,2011:27-30.

[10] 赵永强,梁工谦.可用度限定的装备定期预防置换维修策略研究[J].航空制造技术,2013,1(2):134-137.

Research on Availability and Cost Curve Based on METRIC

LIU Jianchao1JIANG Peng1HAN Baoyu1GUO Shaochen1ZHANG Wei1

(1. Naval Aviation Institute, Huludao 125001)(2. No. 92367 Troops of Navy, Qingdao 266041)

Through the analysis of the method of multistage repairable spares management study, a plan based on the optimization of repairable aviation equipment spare parts inventory method is put forward. In view of the equipment on the spare parts, the optimal inventory of all the airline sector, air demand of spare parts and other parameters are calculated, so as to seek the warehouse shortage for minimum, equivalent to seek the highest equipment availability. Finally the suggestion in the form of the optimal curve of availability and cost in the form of recommended spare parts is given to the aviation sector executives.

inventory, METRIC model, expected shortage

2014年10月11日,

2014年11月28日

刘剑超,男,硕士,助教,研究方向:飞机发动机。

TP391

10.3969/j.issn1672-9730.2015.04.033