基于双轴转台的捷联惯导系统姿态精度评定算法*

张和杰 李京书

(1.北京西三环中路19号 北京 100048)(2.海军工程大学电气与信息工程学院 武汉 430033)



基于双轴转台的捷联惯导系统姿态精度评定算法*

张和杰1李京书2

(1.北京西三环中路19号 北京 100048)(2.海军工程大学电气与信息工程学院 武汉 430033)

系统姿态精度是惯导系统的重要指标之一。针对系统的姿态精度,尤其是动态姿态精度因缺乏姿态基准而难以评定的问题,提出一种基于双轴转台的惯导系统姿态精度评定算法。首先对姿态误差角建模,利用惯导组件不同航向角所确定的旋转矩阵第三行三列的元素不含有航向角信息的特点,在无北向基准的情况下,求解出惯导和转台的安装误差角,进而得到惯导姿态误差,此姿态误差即可反映系统姿态精度,最后,进行了光纤惯导系统的精度评定试验。结果表明,算法在转台无需北向基准条件下可有效标定出惯导系统姿态误差和安装误差,其流程简单、适应性好,可为系统精度评定提供参考。

标定; 安装误差; 惯导系统

Class Number U666.1

1 引言

导航系统是现代武器装备重要的组成部分,其精度和性能严重制约着武器装备效能的发挥[1]。针对惯导系统的研究主要集中在惯性测试组件快速、准确的误差标定、系统误差的补偿和抑制、系统初始对准及系统综合校正等方面。通过上述研究,可有效抑制各误差源在系统内的传播,提高有限器件水平下的系统精度。

同时,不同的应用需求对惯导系统的精度要求也不尽相同,根据惯导系统提供的信息种类,衡量惯导系统的精度指标主要包含姿态精度(在此包含纵摇、横摇、航向)、速度精度、位置精度。针对惯导系统速度和位置精度的评定,可以通过GPS、计程仪、测速仪等设备给系统提供较高精度的速度和位置基准,利用基准信息与惯导系统输出来评定系统精度。对于惯导系统在静态条件下的姿态精度,可以通过固定的水平基准进行评定。文献[7]提出了一种双轴转台的八位置调平及失准角估计方法,通过一个圆周上的八位置的失准角来调整转台地脚由此获得较高的水平基准。但是,对于系统的动态姿态精度评定难以获得高精度的姿态基准。目前常见的动态姿态精度评定一般通过光学方法获得系统姿态基准。利用光学测量系统进行系统姿态精度的评定方法需要复杂的光路设计,同时所需设备众多,对环境要求高。同时,在进行惯导系统精度评定时,在测试设备和系统之间不可避免的存在安装误差,该安装误差与系统本身姿态误差耦合,最终影响系统的精度评定。因此,如何在有限的环境条件下,有效分离系统安装误差和姿态误差,准确、合理的评价出系统的姿态精度成为惯导系统技术也成为惯性系统技术研究的重要方面。目前,对于无姿态基准条件下,惯导系统动态姿态精度评定的研究鲜有报道。根据文献[7]方法可有效获得状态的水平基准,从而进行系统纵横摇精度的估计。但是对于系统的航向精度,难以获得转台的北向基准。

针对利用光学方法进行惯导系统姿态评定对实验条件要求高,同时评定时基准信息难以获得的问题,本文提出了一种基于双轴转台的惯导姿态系统动态精度评价算法。算法利用航向轴的旋转,求解出载体安装在平台上得的误差角,由于安装误差角与惯导的运动形式无关,利用所求得的安装误差角求得惯导动态情况下的惯导输出误差。算法的主要优势在于它仅仅要求转台具有水平基准,然后利用航向转动的特殊性,求解出惯导误差。并且利用实测数据验证了此算法的有效性。

2 姿态角误差建模及求解

2.1 传统安装误差定义

为了分析和讨论方便,首先进行坐标系约定。

1) 理想导航坐标系n:惯导系统进行导航解算的坐标系,本文选取当地地理坐标系为理想导航坐标系。

2) 计算导航坐标系n:由于存在计算误差,实际的导航坐标系与理想坐标系存在偏差,该偏差即表征了惯导系统的姿态精度。惯性测试组件的输出通过相应的坐标变换后在该坐标系内进行导航信息解算。

3) 转台坐标系b:由转台台体的旋转轴确定的坐标系,xb、yb、zb分别沿旋转轴指向右、前、上。

4) 转台零位坐标系B:由转台姿态的输出值为零时的转台坐标系。

5) 载体坐标系b′:由惯导系统确定的坐标系,原点位于质心,xb′、yb′、zb′分别指向右、前、上。

6) 载体坐标系b′:由惯导系统组件确定的坐标系,原点位于质心,xb′、yb′、zb′分别指向右、前、上。

2.2 姿态误差角建模

若约定绕一个轴的旋转为基本旋转,则两坐标系间任何复杂的角位置关系都可以看作有限次基本旋转的复合,变换矩阵等于基本旋转确定的变换矩阵的连乘,连乘顺序依基本旋转的先后次序由右向左排列。根据坐标系的相互关系,则由坐标系依次旋转可得:

(1)

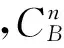
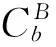
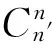
(2)

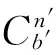
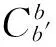
2.3 姿态误差角模型简化

对姿态评定来讲,关键是需要找到两个基准,即:水平基准和北向基准。文献[7]给出了一种双轴转台的八位置调平及失准角估算,能够将转台台面最大失准角控制在3″以内,可以认定水平基准可以得到。而北向基准的确定相对困难,一般由高精度的陀螺经纬仪或者瞄北极星测量获得,然后通过光学原理,将转台转动到和北向平行的方位,这就需要在台体安装可微调的反光镜,并且一次瞄北完成,每次实验前转台是否一直维持北向也很难考核,因此本文假定转台零位坐标系是具有足够精度的水平基准却不具有北向基准,也就是转台零位坐标系和理想的导航坐标系仅仅相差一个航向角,此假设分别通过零位静态实验和俯仰轴保持不变仅旋转主轴的动态实验验证,实验验证此假设合理。

(3)

3 载体坐标系和转台坐标系的安装角求解

3.1 安装误差求解过程

首先让惯导在水平航向旋转,将式(2)变换得:

(4)

由于惯导在水平面内旋转,状态零位坐标系的转台输出为:γ1=0,θ1=0,则:

(5)

将式(1)、(3)和(5)带入式(4),取等式第三行和第三列的元素相等,得:

-C11sinγcosθ+C12sinθ+C13cosγcosθ=-φy

(6)

-C21sinγcosθ+C22sinθ+C23cosγcosθ=φx

(7)

-C31sinγcosθ+C32sinθ+C33cosγcosθ=1

(8)

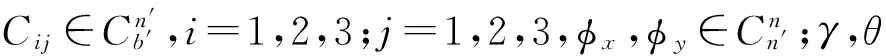
通过三个不同航向位置的惯导输出建立起的变换矩阵,利用式(8)即可求解出平台坐标系和载体坐标系的误差角输出,为了辨识误差角,避免求解矩阵出现奇异值,因此选取的三个航向点应具有足够的角度,不能连续取值,但随时间增长,由于存在舒拉周期以及陀螺漂移等影响,所采数据点的时刻也不能相差时间过长。

由于惯导输出存在量测误差,其中还耦合了温度漂移、角度随机游走、旋转过程的不严格水平等不确定因素带来的误差,其值具有无法确定性,因此不宜利用式(6)、式(7)进行安装误差求解,由于式(8)在理论上比较严格,因此考虑利用式(8)对安装误差角求解,本文使用最小二乘方法处理,得载体坐标系和平台坐标系的安装角,其求法具体如下:

取三个不同航向点根据式(8),有:

An×3X3×1=In×1

其中:

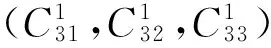
为了避免An×3出现奇异,需要选取一定时间间隔的数据,得:

则安装误差角为

(9)

3.2 航向姿态角求解

重写式(2)

P= (C11X1+C12X2+C12X3)φy

-(C21X1+C22X2+C23X3)φx

+(C31X1+C32X2+C33X3)

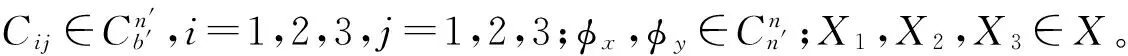
由左边和右边的第三行第三列相等的特殊性,有:

cosγ1cosθ1= (C11X1+C12X2+C12X3)φy

-(C21X1+C22X2+C23X3)φx

+(C31X1+C32X2+C33X3)

进而通过式(6)和式(7)求解出惯导的姿态误差角:

(11)

4 实验验证

4.1 静态实验

论文所提方法为一种通用的惯导系统姿态评定算法,适用于各种惯导系统或捷联姿态系统的姿态精度评定。针对光学陀螺捷联惯导系统已经成为惯性系统技术发展的主要方向,以实验室购置的航天33所研制的光纤陀螺捷联惯导系统FINS为例,验证本文算法的对系统姿态评估的有效性。图为FINS实物图,其标称的姿态误差是0.01°。

图1 FINS的实物图

首先进行静态实验,使转台处于物理零位,然后缓慢旋转主轴,使转台在保持水平的情况下处于不同的航向点,待转台完全静止稳定后,采集转台数据和相应的同时刻同位置惯导数据,图2是将FINS系统置于双轴转台进行实验的实物图,记录一组静态数据如下:(实验转动了10个位置点,转台台体保持水平,仅旋转方位轴,记录不同方位点的惯导输出数据)。

图2 FINS安装于双轴实验转台实验图示

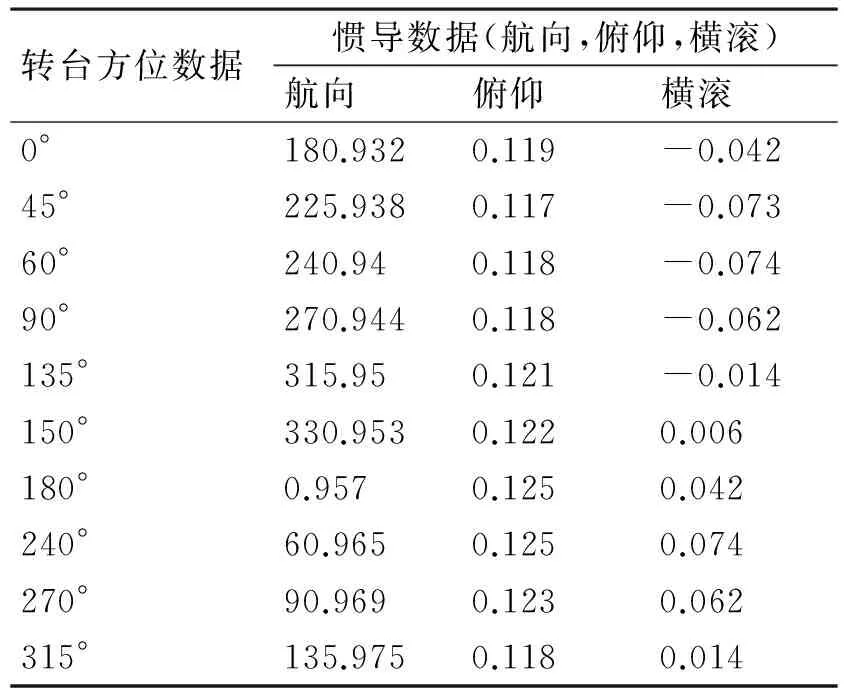
转台方位数据惯导数据(航向,俯仰,横滚)航向俯仰横滚0°180.9320.119-0.04245°225.9380.117-0.07360°240.940.118-0.07490°270.9440.118-0.062135°315.950.121-0.014150°330.9530.1220.006180°0.9570.1250.042240°60.9650.1250.074270°90.9690.1230.062315°135.9750.1180.014

利用以上静态数据,通过安装角求解方法求得:

4.2 动态实验

动态条件下惯导误差是评价惯导是否符合标准的重要指标。由于转接板的惯导安装误差相对稳定,在动态试验中,会带来较大的量测误差,安装角在静态环境下的求解要比动态情况下要精确得多。因此动态实验中的安装参数依然选用静态实验的估计结果。

将惯导系统安装于双轴转台上,将双轴转台的主轴调置零位,参考文献[7]的方法将转台调平,将调整后的位置设定为转台物理零位,假设转台沿航向轴旋转时,旋转平面可以被认定是水平的,转台的俯仰输出应该近似为零,为了说明本文假设的合理性,现给出了转台沿主轴分别以旋转速率为1°/s旋转时,转台的俯仰输出角数据,如图3所示。

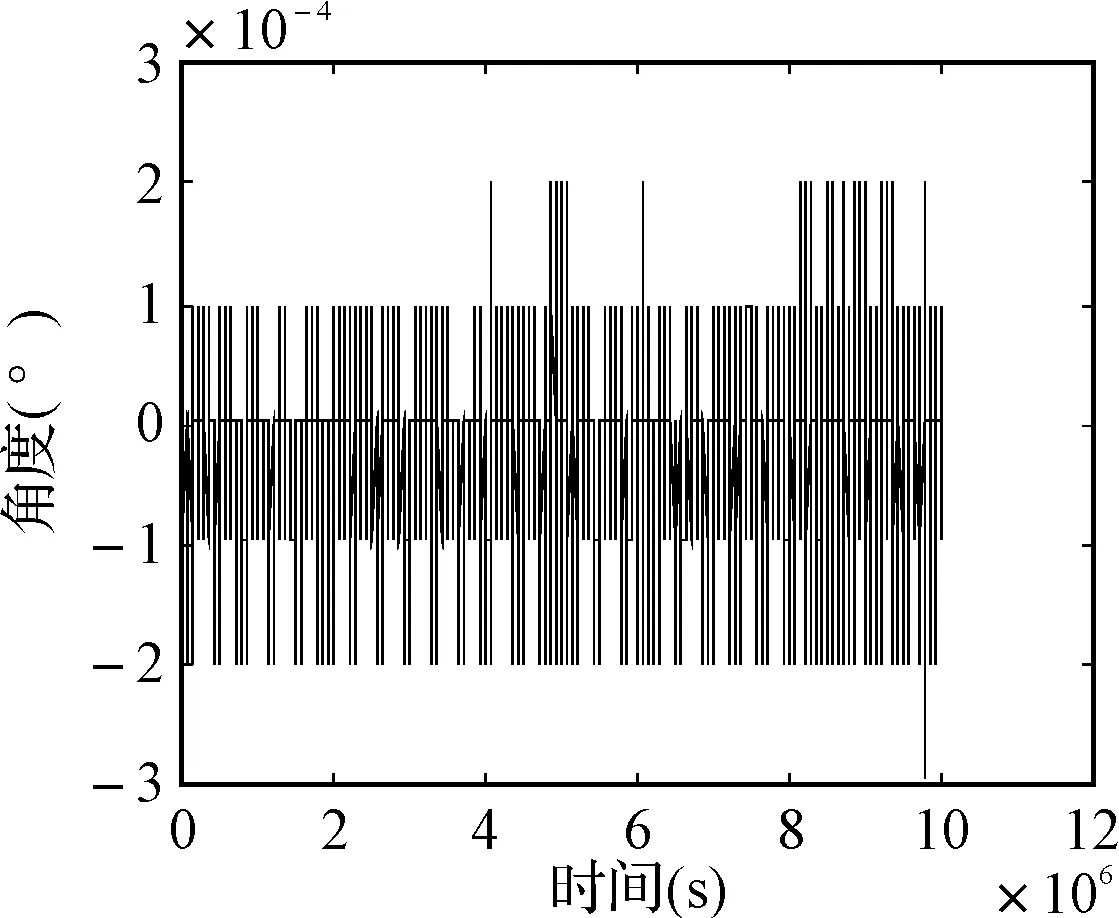
图3 航向转速为1°/s时转台俯仰输出

由图1可以看出俯仰输出角度都是在10-4量级,其中转台的采样率为1000Hz,惯导的采样频率为10Hz。可以认为满足旋转过程中近似水平的假设条件。

然后根据式(11)求得惯导误差:

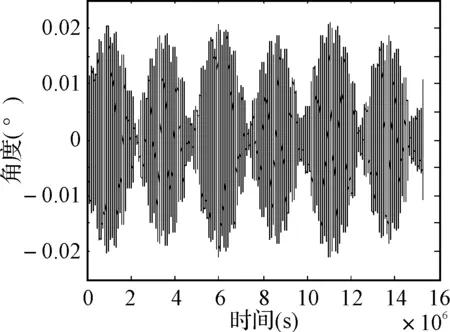
图4 φx的误差曲线

图4、图5给出了转台航向转速分别为1°/s的速度旋转时,惯导系统的姿态误差曲线,由图可以看出整个误差水平在10-2,两个方向的系统误差的标准差为0.008931,0.008484。由此可以得出结论,所测惯导设备精度达到了预期精度。

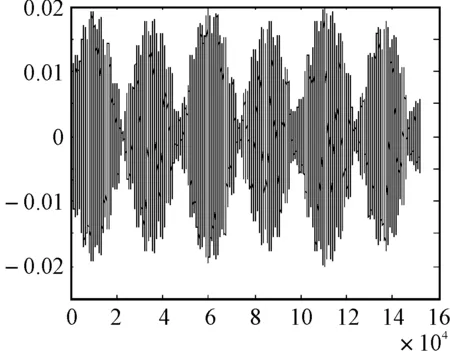
图5 φy的误差曲线

本算法的本质是利用航向旋转的特殊性,较为精确的求解出惯导系统置于转台上的安装误差角,然后利用计算机导航坐标系和理想导航坐标系的投影关系得到惯导的系统误差。因此可以认为是一种通过对安装角度的标定求解惯导的系统误差。从而对惯导进行评定。

5 结语

本文提出一种捷联惯导系统姿态误差评定算法,该方法在转台没有北向基准,利用在转台航向旋转的特殊性,通过采集转台不同航向位置时惯导系统静态输出,求解出组件IMU通过过渡板安装的不水平误差角,由于不水平安装误差角在旋转过程中相对稳定,继而将求得的不水平误差角带入误差方程,根据坐标系的投影关系得到惯导系统的纵横摇误差。此方法避免了实验条件中要求较为苛刻的北向基准,有效地对惯导系统的精度进行了验证。

[1] 张红良,武元新,查亚兵.高精度惯测组合标定误差分析[J].国防科技大学学报,2010,32(1):142-146.

[2] 刘百奇,房建成.一种改进的IMU无定向动静混合高精度标定方法[J].仪器仪表学报,2008,29(6):1250-1254.

[3] 查峰,许江宁,覃方君.一种高精度无定向的光纤陀螺IMU转停标定方法[J].中国惯性技术学报,2011,19(4):387-392.

[4] 蔚国强,杨建业,张合新.激光陀螺捷联惯导系统的无定向快速标定技术研究[J].中国惯性技术学报,2011,19(1):21-27.

[5] 査峰,高敬东,许江宁,等.光学陀螺捷联惯导系统发展与展望[J].激光光电子学进展,2011,7(1):172-177.

[6] 田亚军,周刚,胡军照.捷联惯导系统姿态算法实现及工程应用[J].2011,32(1):10-13.

[7] 李海兵,朱志刚,胡延祯.双轴转台的八位置调平及失准角估算[J].2012,20(1):122-126.

Inertial Navigation System Attitude Accuracy Evaluation Algorithm Based on the Turntable/Strapdown

ZHANG Hejie1LI Jingshu2

(1. No. 19 Central Xisanhuan Road, Beijing 100048) (2. College of Electricity and Information Engineering, Naval University of Engineering, Wuhan 430033)

The attitude accuracy is one of the important indicatiors in inertial navigation system. For the attitude accuracy problems, especially the difficulty in assessing dynamic attitude accuracy, an inertial navigation system attitude accuracy evaluation method based on turnable strapdown is proposed. Firstly, posing error angle is modeled, and the characteristic that the third line three columns element of the rotation matrix determined by different course angles don’t contain the information of course angle, is used to compute the installation error angle between inertial navigation and table in the absense of north benchmark, thus obtaining the inertial attitude error which can reflect the attitude accuracy of the system. Finally, the accuracy evaluation test of optical fiber inertial navigation system is conducted. The result shows that the algorithm can effectively evaluate the attitude error and installation error of inertial navigation system without north benchmark, which has simple process, good adaptability, and can provide reference for system accuracy evaluation.The attitude accuracy inertial navigation system is one of the important indicators. According to the attitude accuracy, especially for dynamic attitude accuracy lack of available precision benchmark, an attitude accuracy evaluation algorithm is proposed based on a turntable/the inertial navigation system. First posing error Angle modeling, making use of the characteristic that the third line three columns element of the rotation matrix determined by different course Angle of the IMU don’t contain the information of course Angle. In the absence of north to benchmark, solve the inertial navigation and table installation error Angle, and then get the inertial attitude error, this attitude error can reflect the system attitude accuracy, finally, the optical fiber inertial navigation system precision evaluation test. The results indicate that the algorithm in the turntable benchmark conditions without north can effectively evaluate the inertial navigation system calibration attitude error and installation error, the method have simple process, good adaptability, can provide reference for the system precision evaluation.

calibration, alignment error, inertia navigation system

2014年10月5日,

2014年11月27日

国家重大科学仪器开发专项(编号:2011YQ12004502);“十二五”预研项目;国家自然科学基金(编号:61104184,41071295);湖北省科学基金(编号:2011CDB054)资助。

张和杰,男,博士,高级工程师,研究方向:惯性技术及应用。李京书,男,博士,讲师,研究方向:惯性技术及应用。

U666.1

10.3969/j.issn1672-9730.2015.04.013