考虑来流边界条件不确定性的数值模拟方法
吴逸飞,邹正平
(1.南昌航空大学飞行器工程学院,南昌330063;2.北京航空航天大学能源与动力工程学院,北京100191)
0 引言
随着计算技术的飞速发展,研究各种流体流动的重要方法包括计算流体力学(CFD)数值模拟、传统的理论分析和试验测量方法。采用数值模拟方法研究问题时常常会简化,例如几何和物理模型的简化、物性参数和边界条件的近似等,造成实际情况与结果之间存在差异[1]。在航空发动机研制中,受认识、设计技术、制造工艺及装配等客观因素的限制,实际装机后系统和各部件所达到的性能水平与理论设计值必定存在不确定性的偏差[2]。在涡轮设计和加工过程中,在转静子之间的轴向间隙及泄漏流、强度和加工方面存在的叶片叶根倒角、叶形的偏差、圆机匣及转子偏心等造成的转子周向非均匀叶尖间隙等问题,都会导致涡轮真实几何条件与原始理想设计存在偏差,从而造成涡轮实际与设计性能的偏差[3-5];同时,在涡轮工作过程中,温度与离心载荷等产生受力变形、磨损、高温氧化、热腐蚀、烧蚀、表面产生凹坑或有尘物堆积等情况[6-7],导致零件性能随工作时间发生退化。在数值计算和试验中,合理的边界条件是重要影响因素之一。Garg等[8]研究不同射流入口边界条件可导致射流出口下游高达60%的换热系数差异。在航空发动机中,燃烧室出口温度分布、高自由流湍流度和热条纹等参数影响第1级静叶传热;中、低自由流湍流度、上游静叶片后缘的不稳定尾流、热条纹以及旋转影响第1级动叶传热[9]。文献[10-12]表明来流的速度分布、湍流强度、温度分布、压力分布、质量流量和雷诺数等气动热力边界条件对流体的流动有重要影响。在数值模拟方法应用中,不同的物理模型对结果产生不同的影响,例如有/无黏、定常/非定常、湍流模型、多相流动、化学反应等[13]。20世纪70年代中期前,叶轮机械内部流场的数值模拟大都基于无黏流体流动模型。但是,无黏流动假设改变了流体的物理属性,在数学上使流动方程及相应的定解条件发生了本质变化,应该考虑采用黏性流体流动模型[14]。叶轮机内存在不同尺度、频率和类型的非定常流动现象,采用全3维非定常数值模拟研究其内部一些固有的非定常流动现象,可进一步提高气动热力性能[15]。
本文针对气动热力学边界条件不确定性的数值模拟方法进行探讨,分析边界条件与真实情况的差异对数值模拟计算结果的影响。
1 试验方法
目前流体中不确定性分析主要指模型参数不确定性对其输出参数的影响,即不确定性在流场中的传播,且不确定性变量为服从概率分布的随机变量[13]。
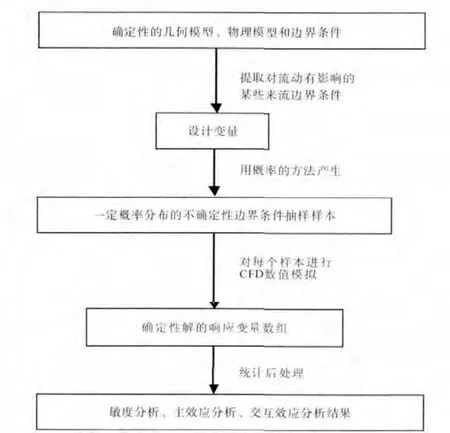
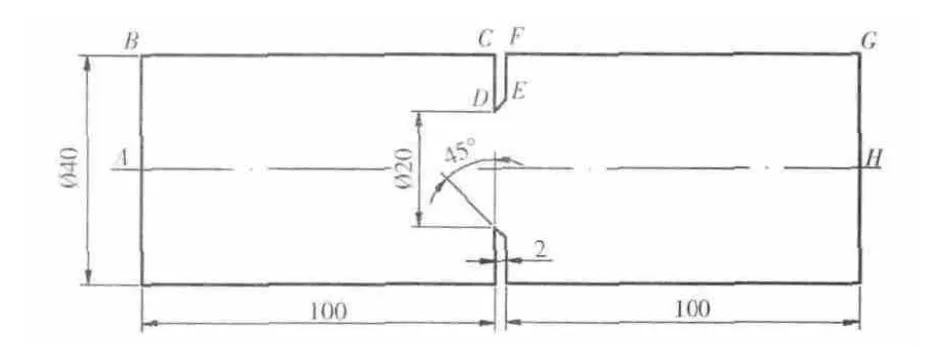
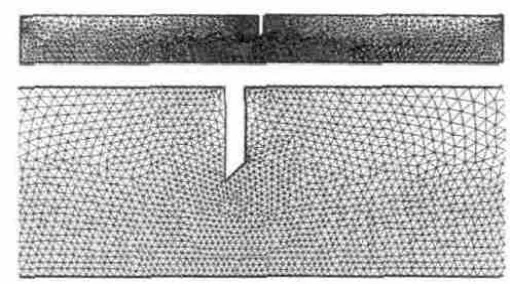
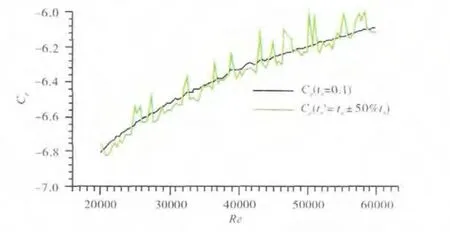
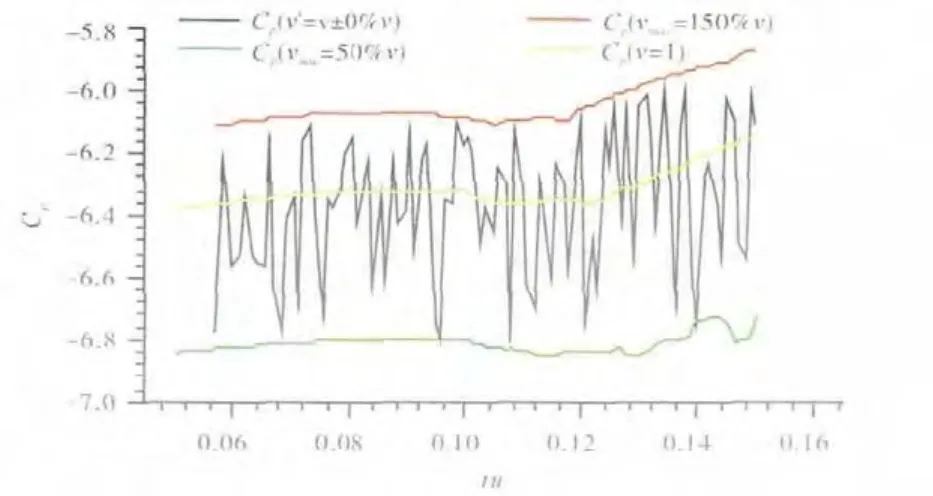
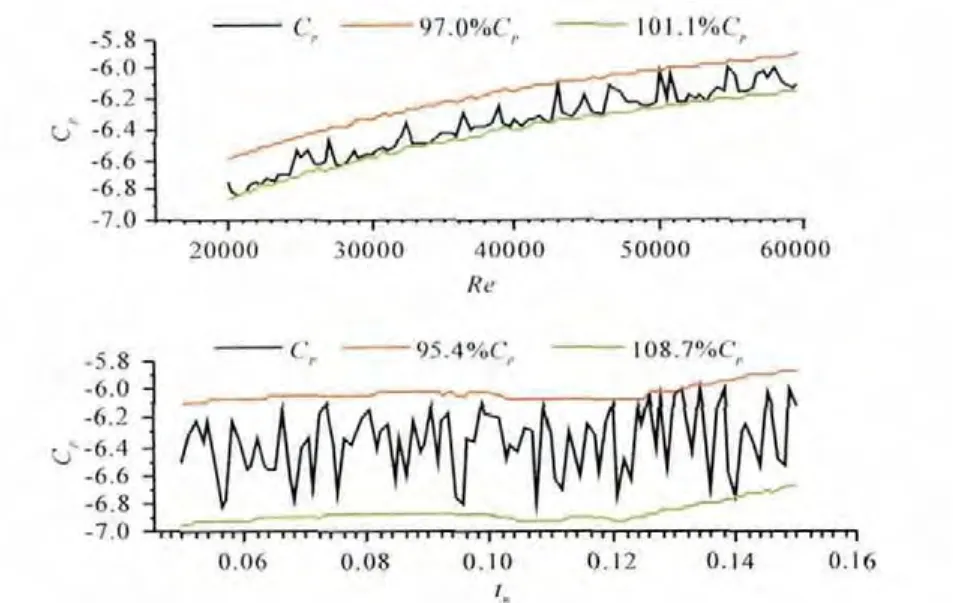
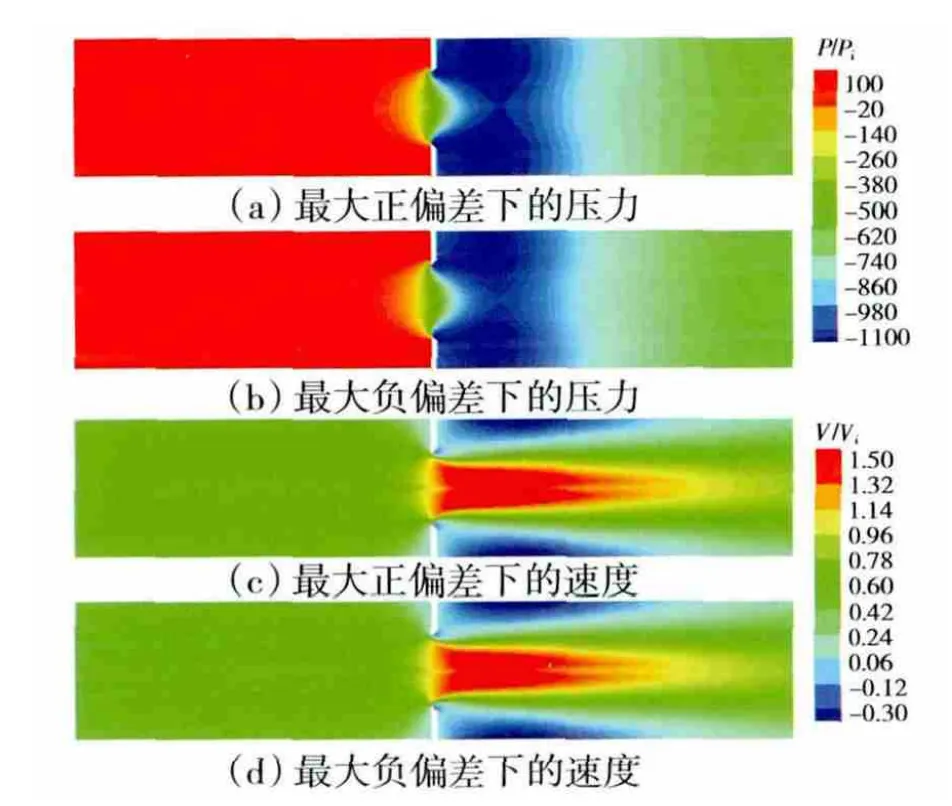
蒙特卡洛(MC,Monte Carlo)[16]方法是随机分析常用的方法,其实质是通过大量随机试验,利用概率论解决问题。主要优点是其敛散性依赖于独立的随机参数个数,得到的结果是随机变量。因此,在给出点估计后,还需要给出该估计值的波动程度及区间估计。缺点是高精度的计算结果需要大量的随机数即需抽取大量样本,因此计算成本较高且效率低。拉丁超立方抽样(LHS,Lat in Hypercube Sampling)是1种多维分层抽样方法,合并了随机和分层抽样的优点,是最好的小样本蒙特卡洛方法之一[17]。对于多个随机变量的输入,分层抽样需要将输入的样本空间等概率化为N个区域。工作原理是首先定义参与计算机运行的抽样数目N;其次把每次输入等概率地分成N列,xi0 图1 LHS方法抽样 假设关于输入变量的线性函数 利用MC和LHS抽样方法分别估计均值,结果为 标准误差分别为 本文采用试验设计(DOE,Design of Experi-ment)[18]方法进行研究。首先以某一确定性解为基础,对具有不确定性的设计变量统计LHS抽样产生随机变量的相关参数;然后对所有抽取的样本进行确定性解,对这些确定性结果进行统计后得到响应变量;最后分析不确定性设计变量对响应变量的影响。应用CFD软件,可避免出现修改现有求解器而可能造成新误差的风险。具体流程如图2所示。 图2 边界条件不确定性数值模拟方法流程 DOE通过改变1个系统的输入来观察输出的情况。目的是确定哪些设计变量对响应的影响最大;通过设定有影响的设计变量水平,以使响应达到或尽可能接近期望值,并使其分散度(或方差)尽可能减小,最大限度地减小不可控参数对响应的影响。通过试验数据的分析探索设计空间,得出设计变量对响应的影响,并以此作出设计决定。 对确定性解的响应变量数组进行数据分析处理,包括敏度分析、主效应分析、交互效应分析等,如用帕累托法(Pareto)得出来流边界条件对流体的影响。 采用DOE法需要对每个抽取的样本进行CFD数值模拟计算,为了节省计算时间和成本,本文仅给出1个简单算例说明来流边界条件不确定性数值模拟的方法在原理和流程上是可行的。例如:孔板流量计是通过测孔板前后的压力差来计算管道中的流量。假定几何和物理模型均不变,仅考虑来流边界条件变化,确定其对孔板前后压力变化的影响。 根据原理对孔板流量计模型进行简化,如图3所示。从图中可见,可以构建对称轴以上的部分为模型对2维对称流动问题进行数值模拟。 图3 孔板流量计简化模型 设定计算流体为水,流动形态为湍流,采用κ-ε模型,流动为定常,不可压缩,计算不计重力作用对流体性能的影响。流体入口半径AB=20mm,孔在距离入口100mm的位置,孔板厚度为2mm,内径为20mm;在孔板右侧面切45°,出口端面距孔板右侧100mm。网格划分采用非结构网格,数目为6947个,如图4所示。 图4 网格分布 本算例运用商业软件Fluent进行CFD模拟,设定确定性数值模拟来流边界条件中的湍流度tu和流体进口速度v为设计变量。然后在输出的结果中提取进、出口面压力Pi(面加权平均)、Po为响应目标。采用LHS方法,通过DOE组件对设计变量抽样,样本为100个,分别计算得出响应结果,然后分析每种设计变量对每个响应的影响,得出主效应和Pareto贡献率图。 为了避免2个来流边界条件下不同上下限百分比对流动产生不同的影响,设定二者相同的赋值范围,即上、下限分别为各自150%、50%初值。为了阐述该方法的原理,在赋值时给的范围比较大,以便分析所得边界条件的不确定性能引起流动变化的量突显出来,而在实际情况下的不确定性边界条件变化的范围不一定有这么大。 Cp与Re的关系如图5所示。流动为定常且不可压缩,几何模型也不变。横、纵坐标分别为进口流体的雷诺数Re和对压差无量纲化的压力系数Cp。 图5 Cp与Re的关系 从图中可见,Cp随着Re的增大而增大。当湍流度变化时,Cp在湍流度不变时位置上下波动。 Cp与tu的关系如图6所示。从图中可见,来流速度不变时,Cp变化较平缓,在tu=0.10~0.13之间最小,随着tu增大则Cp也增大。当来流速度发生变化时,Cp则会在来流速度不变时的位置上下剧烈波动,且在最大、最小速度压力系数值的范围之内。 图6 Cp与tu的关系 可见,来流速度和湍流度都能引起压差的变化,如图7所示。从图中可见,tu变化比Re变化使压力系数Cp的波动更剧烈,即tu对Cp的影响要大于Re的影响。 图7 Cp的主效应 在来流速度和湍流度为其各自基准值的±50%的偏差范围,对Cp的影响的最大正、负偏差分别为8.7%、4.6%。来流边界条件对流体影响正负偏差最大的压力、速度云图如图8所示。 图8 来流边界条件对流体影响正、负偏差最大的压力和速度 如果期望得到各设计变量对响应的影响,可以对抽样样本计算所得的数据组进行Pareto法分析,得出来流速度和湍流度对压力系数的贡献率,其中tu和Re对Cp的贡献率分别为64.04%、35.96%。 综上所述,提取来流边界条件为设计变量,通过LHS方法抽样计算及pareto法分析可以得出不同敏感边界条件对流体流动的影响。当来流Re和tu给出初值±50%变化时,得出Cp偏差中最大正、负偏差分别为8.7%和4.6%;Re和tu对Cp的贡献率分别为35.96%和64.04%。 利用该方法可以研究多个来流边界条件共同作用下对流体流动的影响,例如在复杂的流动中,提取多于算例中2个来流边界条件,边界条件之间的交互相互影响关系也远比算例中的复杂,该方法只需要根据所抽样本数进行计算,计算量不会因为提取边界条件种类的增加而增大,抽样数越多计算量越大,所得数据分析则越精确。本方法也可对来流边界条件不确定性的范围进行提前约束,并根据研究对象的具体情况设定,对流体的影响偏差的范围也可以通过数据处理分析得出,又可反推出要达到流体流动的某种状态或某些范围,则需要控制的边界条件的不确定性范围。在研究航空发动机时,可以提取来流边界条件为设计变量,并设定来流边界条件不确定性的误差范围,模拟计算得出压气机或涡轮等的效率误差,分析得出边界条件中对压气机或者涡轮等的效率影响最大的参数,为调控这些不确定性的来流边界条件提供可靠依据。如果对所提取的设计变量进行扩展,比如将几何模型的关键尺寸提取为设计变量,则可研究几何模型不确定性对数值模拟结果与实际情况的差异等。 本文针对考虑来流边界条件不确定性的数值模拟方法进行尝试性研究,分析了对流体流动的影响。算例结果表明,在来流边界条件中湍流度的不确定性对压力系数的影响大于来流速度的。考虑来流边界条件不确定性的数值模拟方法比传统数值模拟方法计算量有所增加,其大小由所抽取样本数决定。该方法可扩展应用到更多来流边界条件不确定且更复杂的流动分析,或应用于其他模型的不确定性数值模拟。 [1] 王晓东,康顺.多项式混沌法求解随机Burgers方程[J].工程热物理学报,2010,31(3):393-398.WANG Xiaodong,KANG Shun.Solving stochastic burgers equation using polynomial chaos decomposition[J].Journal of Engineering Ther mophysics,2010,31(3):393-398.(in Chinese) [2] 邹正平,周琨,王鹏,等.大涵道比涡扇发动机涡轮内部流动机理及气动设计技术研究进展[J].航空制造技术,2012(13):49-54.ZOU Zhengping,ZHOU Kun,WANG Peng,et al.Research progress on flow mechanism and aerodynamic design method ofhigh-bypass-ratio engine turbine[J].Aeronautical Manufacturing Technology,2012(13):49-54.(in Chinese) [3] 张伟昊,邹正平,刘火星,等.叶型偏差对整机环境中涡轮性能的影响[J].工程热物理学报,2010,31(11):1830-1834.ZHANG Weihao,ZOU Zhengping,LIU Huoxing,et al.Effect of profile deviation on turbine performance in whole engine environment[J].Journal of Engineering Thermophysics,2010,31(11):1830-1834.(in Chinese) [4] 白涛.叶片几何偏差对涡轮性能的影响[D].北京:北京航空航天大学,2013.BAITao.The effect of blade deviation on aerodynamic performance of turbine[D].Beijing:Beihang University,2013.(in Chinese) [5] Good hand M N,Miller R J.The impact of real geometries on three-dimensional separations in compressors[R].ASME 2010-GT-22246. [6] Bons J P.A review of surface roughness effects in gas turbines[R].ASME 2010-GT-21004. [7] 费成巍,付黎,柏树生,等.高压涡轮叶尖径向运行间隙非线性动态分析[J].航空发动机,2013,39(2):38-42.FEIChengwei,FU Li,BAI Shusheng,et al.Nonlinear and dynamic analysis of HPT blade-tip radial running clearance[J].Aeroengine,2013,39(2):38-42.(in Chinese) [8] Garg V K,Gaugler R E.Effect of velocity and temperature distribution at the hole exit on film cooling of turbine blades[R].ASME 1995-GT-2. [9] 韩介勤.燃气轮机传热和冷却技术[M].西安:西安交通大学出版社,2005:20-21.HAN Jieqin.Gas turbine heat transfer and cooling technology[M].Xi’an:Xi’an Jiaotong University Press,2005:20-21.(in Chinese) [10] 何玉荣,詹文博,门玉宾,等.速度进口边界条件对鼓泡床流动影响研究[J].工程热物理学报,2009,30(5):789-792.HE Yurong,ZHANWenbo,MEN Yubin,et al.Study of the impact of the velocity inlet boundary condition to the bubbling fluidized bed[J].Journal of Engineering Thermophysics,2009,30(5):789-792.(in Chinese) [11] 况中华.来流湍流度对圆柱绕流特性的影响[J].河北工程大学学报(自然科学版),2013,30(3):21-25.KUANG Zhonghua.Effects of inflow turbulence on the flow around a circular cylinder[J].Journal of Hebei University of Engineering(Natural science edition),2013,30(3):21-25.(in Chinese) [12] 雷林,孙鹏.湍流入口条件对CFD计算结果影响的数值分析[J].舰船科学技术,2009,31(7):32-36.LEI Lin,SUN Peng.The numerical analysis of the impact of the inflows entrance condition on CFD calculation[J].Ship Science and Technology,2009,31(7):32-36.(in Chinese) [13] 康顺.计算域对CFD模拟结果的影响[J].工程热物理学报,2005,26(S1):57-60.KANG Shun.Influence of computational domain on the CFD results[J].Journal of Engineering Thermophysics,2005,26(S1):57-60.(in Chinese) [14] 王子成.湍流模型对叶轮机械内部流动性能模拟结果影响的研究[D].天津:天津大学,2009.WANG Zicheng.The study on simulative flow performance affected by turbulent model in machinery with impeller[D].Tianjin:TianjinUniversity,2009.(in Chinese) [15] 刘宝杰,邹正平,严明,等.叶轮机计算流体动力学技术现状与发展趋势[J].航空学报,2002,23(5):394-404.LIU Baojie,ZOU Zhengping,YAN Ming,et al.Present status and future development of CFD in tur bomachinery[J].Acta Aeronautica et Astronautica Sinica,2002,23(5):394-404.(in Chinese) [16] Landau D P,Binder K.A guide to Monte Carlo simulation in statistical physics[M].United Kingdom:Cambridge University Press,2000:48-55. [17] 万越,吕震宙,袁修开.基于Latin方抽样和修正的Latin方抽样的可靠性灵敏度估计及其方差分析[J].机械强度,2008,30(6):927-934.WAN Yue,LYU Zhenzhou,YUAN Xiukai.Latin hypercube sampling and updated Latin hypercube sampling method for reliability sensitivity and itsvarian ceanalysis[J].Journal of Mechanical Strength,2008,30(6):927-934.(in Chinese) [18] 闫晓东,韩冰.试验设计方法在飞行器性能仿真验证中的应用[J].飞行力学,2012,30(1):79-82.YAN Xiaodong,HAN Bing.Application of experiment design method in performance simulation validation for flight vehicle[J].Flight Dynamics,2012,30(1):79-82.(in Chinese)

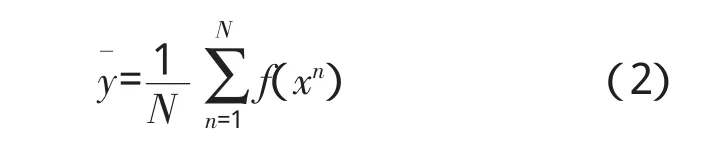
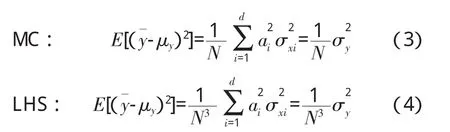
2 算例
2.1 算例模型
2.2 实现方法
3 结果分析
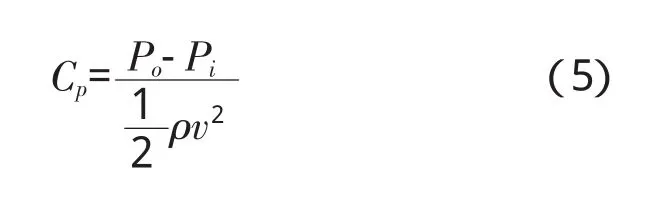
4 总结
5 结束语

