基于非线性谐波法评估压气机转静干涉诱发的强迫响应

孙海，王培屹，郑宁，杨琳，陈育志

（1.中航工业沈阳发动机设计研究所，沈阳110015；2.北京航空航天大学能源与动力工程学院，北京100083）

0 引言

在叶轮机械工程应用中，流体诱发振动导致叶片断裂是1种主要的结构破坏形式。其引发的故障在各类发动机故障中占相当高的比例，且危害较大，是航空燃气涡轮发动机结构完整性和可靠性的主要威胁。而转静干涉是叶轮机械流体诱发强迫振动的重要因素，是由转、静子叶片间的相互转动而产生的非定常流动现象。国内外虽然对由转静干涉引起的尾流激振或者由势流扰动而引起的强迫响应开展了一些研究，但在气动层面非定常脉动压力的计算精度、效率和强迫响应阻尼比的取法以及工程适用性等方面还存在不足。

本文采用非线性谐波法计算非定常流动产生的谐波压力，进而计算该压力在叶片上的强迫响应，计算精度和效率都有一定提升，建立了适合工程应用的、能够评估由于转静干涉诱发的强迫响应的方法。

1 研究背景

一般来说，叶轮机械中的流体诱发振动问题可以分为气动弹性稳定性问题和响应问题2种基本类型。气动弹性稳定性问题对应叶轮机械的自激振动，而响应问题对应强迫振动。与叶片的自激振动相比，在航空发动机的发展历程中，由流体激励诱发的强迫振动所造成的叶片振动破坏故障的次数要远超过由叶片颤振造成的故障。

当前对转静干涉研究较多的是上游叶片对下游叶片的尾流激振和下游叶片的势流扰动对上游叶片非定常表面力的周期性影响。

由于尾流激振力或势流扰动很难用具体的解析表达式表示，因而数值模拟计算尾流激振力是工程中最主要的方法。A.J.Sander和Fleeter[1]研究了1种可用于预测轴向和离心式叶轮机械响应的模型，用于分别计算叶片排在上下游势流和在上游尾迹作用下的强迫响应。结果证明，无论是在轴流还是在离心式压气机中，叶片的强迫响应幅值为同一量级。因此，对于叶片排间距较近的压气机，流势与叶片尾迹具有同样的重要性。Y·T·Lee和J·Z·Feng[2]等研究了不可压流在多级叶排的流动情况，分别研究了转子/静子、静子/转子2种模型。研究指出，在轴向间距为10%弦长时，尾迹效应提供了气动载荷峰值的10%。针对转子数目的影响，研究了转子1/静子/转子2模型，并且转子1和静子、转子2和静子之间的轴向间距可调，发现不同轴向间距最小值到最大值的非定常气动力变化较大。Bjorn Laumert和Hans.Martensson[3]通过3维数值模拟，得出在亚声速工况下，转子叶片压力面上压力值主要受静叶尾流的影响，而在吸力面，压力值主要受静叶势流和尾迹共同影响。由于3维转子叶片沿径向形状不同，使得叶片表面压力分布沿径向也有所不同。叶片表面激振力的大小沿叶根向叶尖幅值逐渐减小。Stuart M[4]提出1种松散的耦合方式对叶片在气流激振力下强迫响应进行预估计算。假定气动力对叶片的模态没有影响，先在ANSYS中计算叶片某一模态的振型和频率，然后将其带入CFD进行频域求解，计算气动力和阻尼力，再带回有限元模型计算该模态下的振动响应。王梅等[5]通过研究均匀叶栅的尾迹引起的高频振动问题，把已有的气动计算方法和强度计算方法整个串起来，为工程应用初步建立起了1个尾流激振情况下叶片振动应力预估的半经验方法。具体是通过计算转子通道流场，得到转子叶片表面的非定常压力幅值沿叶片表面的分布，然后在结构计算中将叶片表面的压力幅值等效地转化为有限元节点上的节点力，再通过有限元方法计算叶片的振动应力。但是，非定常流场计算采用的参数多项式方法精度不足，阻尼的取法也使响应计算的准确性受到影响。孟越等[6]针对转子叶片在前排静子叶片尾流激振[7]情况下的位移和应力进行预估计算，采用3维非定常求解，将3维非定常气动力引入转子叶片有限元结构计算中，对尾流激振情况下叶片强迫响应问题[8]进行瞬态分析。通过分析可知，叶片响应大小与叶片表面所受气动激振力大小、相位和分布有关。宁方飞[9]以1.5级高负荷风扇为研究对象，利用谐波法[10-11]捕获了转子激波向上游的传播，以及转子尾迹对下游静子的影响，结果与常规非定常方法吻合，但并未涉及强迫响应计算。

2 非定常脉动力的研究对象、计算方法和结果

2.1 研究对象

针对某风扇试验件进口可变弯度导向叶片开展数值模拟和试验研究。风扇进口可变弯度导向叶片分为固定部分和可调部分，可调部分可绕转轴旋转调节以满足不同转速转子预旋的需求，由于导叶可调部分只在转轴处固支，与常规静子的2段全部固定相比，更容易受转静干涉影响而被诱发振动。因此，针对后排转子叶片的位势作用对上游可调叶片的强迫响应进行分析。

2.2 非线性谐波法

非线性谐波法（nonlinear harmonic method）能够在一定的计算量范围之内，提供1种介于定常和非定常之间的计算方法，其计算精度较高能够满足计算要求。该方法将流体非定常扰动傅里叶分解为不同阶次谐波叠加。基于求解时间平均和不同谐波阶次的定常输运方程，能够有效地在频域内求解非定常问题，尤其是对于转静干涉问题有较高的计算效率和精度。

转静干涉是叶轮机械流动中最常见的非定常因素，对转、静子通道内流动的影响具有周期性。采用谐波函数逼近，经过周期性扰动近似以及线化假设，可以将N-S方程分解为时均方程和扰动方程，扰动方程的个数由谐波的阶次确定，各阶扰动方程之间相互独立，在谐波的频率给定之后，可以将扰动方程由时域转化到频域。最后在频域内对时均方程和各阶扰动方程耦合求解，就能得到流场各物理量的时均值和各阶扰动值，将其叠加起来就得到近似解。可以通过选择谐波的阶数来控制求解的精度，谐波阶次越高，求解精度也就越高。

引入周期性扰动假设后，在非定常流动中，守恒型变量可以分解为时均值与周期性扰动之和，而每个周期性的扰动可以用N阶谐波来逼近，即

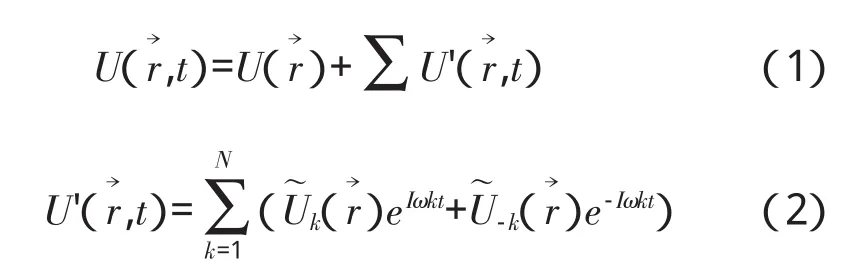
采用有限体积法的守恒型非定常流动方程可表示为

式中：Ωi为网格单元的体积；Fc和Fv分别为离散的对流项和黏性项；S为面积；Q为源项。

具体展开式见文献[12]。展开式中包含的未知数数目是原N-S方程的2N+1倍，求解谐波方程仅相当于求解2N+1个时刻的定常方程。理论上，计算的谐波阶次趋于无穷，其计算结果应当趋近于时间推进的非定常求解结果。一般选取前若干阶（小于5）即可满足工程需求。而且，一般认为，第1阶非定常扰动在幅值上占绝对主导地位（对于尾迹或势流造成的非定常现象），高阶扰动因其频次过高，其距风扇叶片低阶共振频率过远，因此影响较小。

2.3 计算设置及结果分析

网格使用AUTOGRID5生成。Vilmin认为若要成功运用N L H法模拟叶排间的流动状况，上下游叶片周向网格数需要达到一定要求，具体见文献[13]。根据网格数目限定，做出风扇网格，采用NUMECA的Fine进行计算。

以该多级风扇试验件作为流场计算对象。计算时给定进口总温28815K，进口总压101325Pa，给定出口靠近轮毂位置静压值，且静子出口静压满足简单径向平衡方程。采用Harmonic Method进行非定常计算。非定常流场求解以相同进、出口边界条件下的定常结果为初场。为提高计算效率，每个扰动的谐波数设置为2，每个叶排最大的扰动数设置为2。

风扇进口可调导叶第1阶谐波压力实部、虚部及幅值如图1所示。第1阶谐波压力反映了后排转子的非定常势流影响，主要分布在可调导叶表面上半部，由此判断，谐波压力幅值较大区域可能会引起较大的强迫响应。

风扇后排转子50%、90%叶高相对马赫数如图2所示。后排转子马赫数图中的空白部分为超声区。可调导叶表面依旧是谐波压力幅值。在转子90%叶高吸力面有较强激波，而在50%叶高处没有激波。由于可调导叶和转子存在相对转动，转子上半部分存在的激波通过势流作用不断扫掠前排可调导叶，影响可调导叶上半部，尤其影响靠近尾缘的后半部分边界层状况，造成较大的谐波压力脉动。

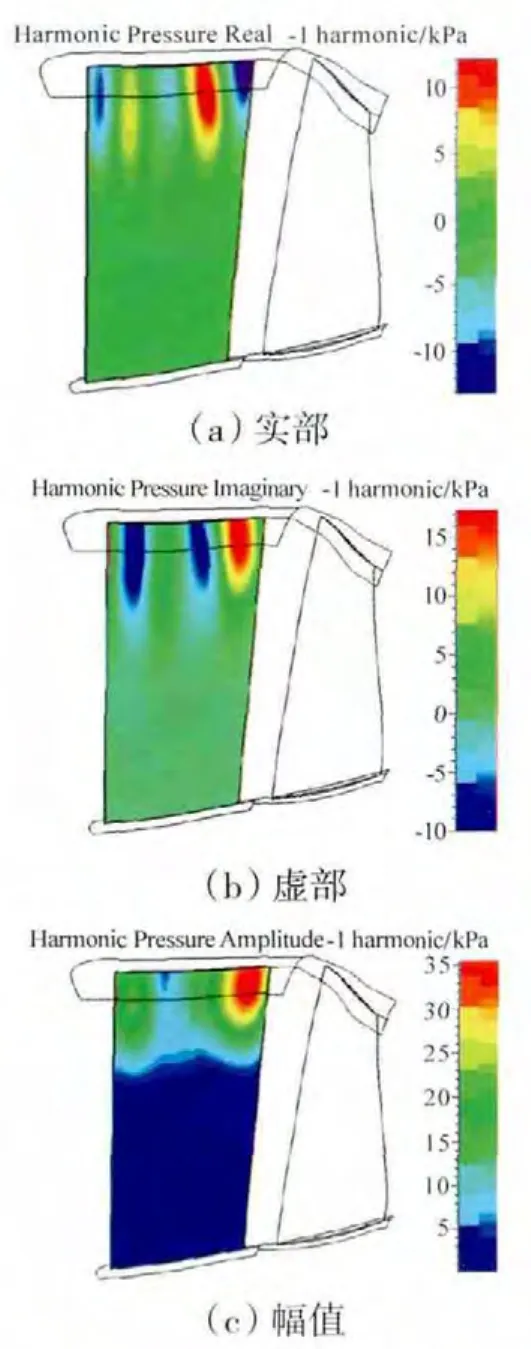
图1 风扇进口可调导叶第1阶谐波压力

3 强迫响应分析

本文建立的强迫谐响应的分析模型，应用MATLAB和ANSYS的2次开发语言APDL编制流场与结构的接口程序，将流场计算的3维非定常激振力完整加载到结构中，并对结构进行强迫响应瞬态分析，具体计算流程如图3所示。

选取可调导叶部分（略去固定支板）进行有限元建模，叶片在厚度方向分为2层，对前缘和尾缘进行了适当加密，整体网格数约为1.6万，如图4所示。模拟可调导叶真实的约束情况，给定叶尖前缘部分全约束，叶根前缘部分周向和轴向约束，可绕径向轴转动。

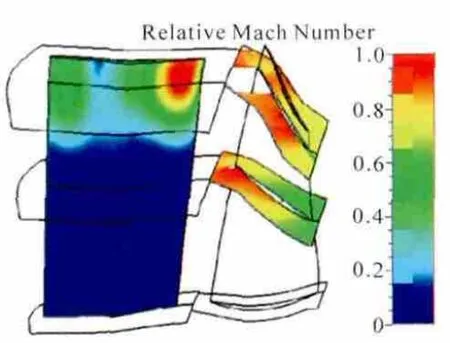
图2 风扇后排转子50%、90%叶高相对马赫数和第1阶谐波压力幅值

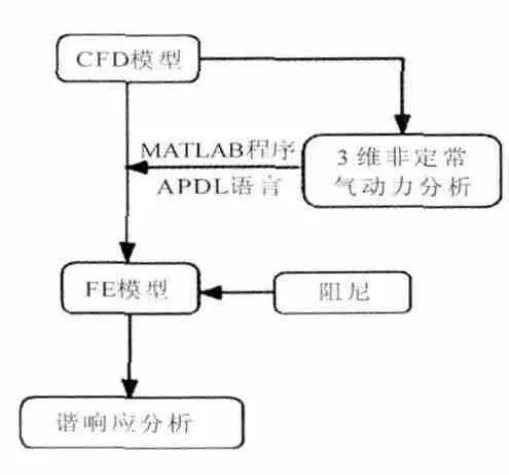
图3 强迫谐响应分析系统

图4 有限元模型及施加约束

利用SURF154单元进行脉动压力的传递，利用F E M模型表面节点以及CFD模型靠近叶片的第1层网格节点插值，如图5所示。图中红色节点为F E M模型可调导叶部分，蓝色为CFD模型（包括固定支板）。程序自动寻找较近点进行插值，因此多余的固定支板不影响插值结果。

对叶片进行模态分析，找寻到与势流激励相近的模态阶数。在气动载荷的激励下，进行谐响应分析，模态阻尼比取5e-4von Misesstress如图6所示。除去转轴处固支带来的应力集中，叶身振动应力幅值约为20MPa，与试验应力水平相当。

不同模态阻尼比振动响应分析的动应力结果见表1。从表中可见，模态阻尼比是振动响应分析的重要影响因素。如果试验能够获得较为准确的阻尼数据，则采用该方法能够较好地评估叶片由于尾流激振或势流扰动造成的强迫响应。然而，在工程设计阶段，没有试验件的生产，无法通过试验获得阻尼数据，因此很难准确确定模态阻尼比，导致谐响应分析存在较大误差。这就要分析在不需要阻尼比的情况下，评估这种强迫响应造成的高周疲劳水平。

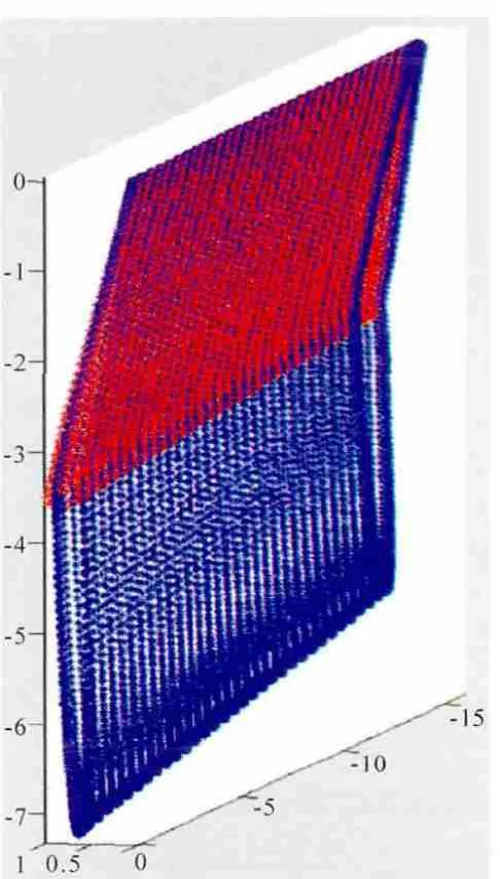
图5 CFD与FEM模型插值节点

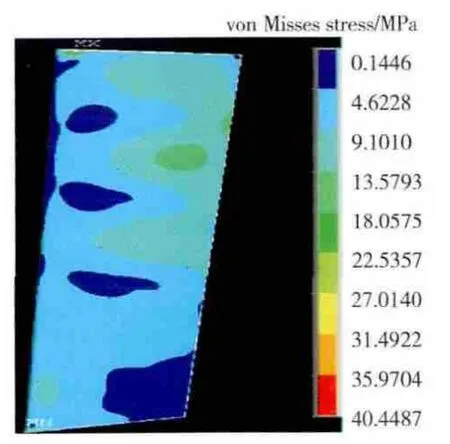
图6 阻尼比为5e-4时谐响应von Missesstress

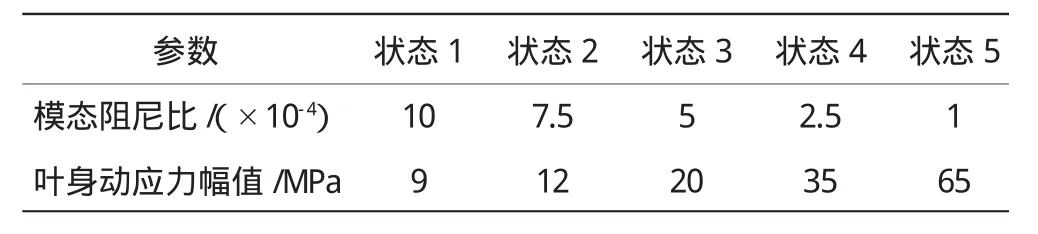
表1 不同模态阻尼比下响应分析的动应力结果

4 模态激励因子评估强迫响应

如前所述，在叶轮机械中，由转静干涉引起的叶片强迫响应振动主要是以转速为基频的周期性激励。尤其是在某些特定阶激励频率（可引起危险共振的，如第n阶激励频率）作用下叶片的强迫响应。

与一般激励不同，这里的激励为非同步激励，即除了频率以外，在任意时刻，流场中的任意1点（包括叶片表面上）的作用力由2个参数确定，即：幅值和相位。这2个参数均是点的空间位置坐标的函数。

尾流激励或者是势流扰动所具有的非同步激励场的特性，决定了叶片的强迫响应既取决于激振力场又取决于模态位移场。模态激励因子可以包含这2方面性质，能够对某阶共振的相对危险性做出一定评价。

激振力、模态位移都以场的形式出现，其中激振力场又是场的复数形式的叠加。这就使得激励-响应之间的关系可以从场的角度描述。可以引入欧氏空间的相关概念，从数学上讨论激励场与模态位移场的空间相对位置对叶片响应的影响，从理论上给出模态激振因子的解释。

定义模态激励因子[14]

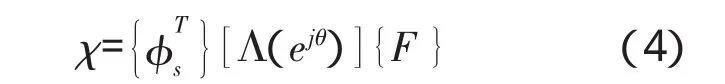
式中：｛F｝为激励的幅值向量；[Λ（ejθ）]为以激励相位为对角线元素的对角矩阵；｝为对系统质量矩阵归一的第s阶模态向量。模态激励因子的几何意义为尾流激励的空间分布与叶片振动模态的夹角。

激励因子的幅值反映了尾流激励或势流扰动在某阶模态投影的大小；相角反映了激振力场与模态位移场间的夹角，夹角越小，作用越强。

以某风扇导向器叶片与转子轴向间距改变对尾迹激振的影响为对象，对非同步激励场作用下叶片高激振力场阶共振的危险性评定方法进行校核，结果如图7所示。

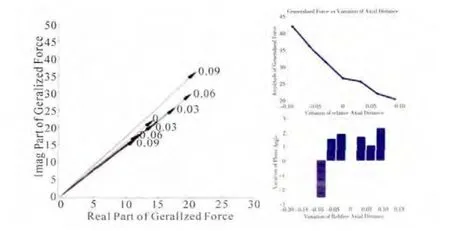
图7 激励因子及其和相角随轴向间距变化

从图中可见，随着轴向间距的增加，激励因子的模呈下降趋势，这与实际物理现象吻合；相位变化，反映了上游尾迹进入下游转子通道的时间先后发生了变化。可见，激励因子能够直观定量地反映出结构、气动参数变化对结构共振响应造成的影响，能够真实地反映物理实际。

对可调导叶，在计算过程中提取载荷向量和模态向量，计算出激励因子，如图8所示。按经验，模态激励因子与之前计算的振动应力水平相当。本文虽然对转静干涉中的后排对前排的势流扰动进行计算，其方法也同样适用于尾流激振。

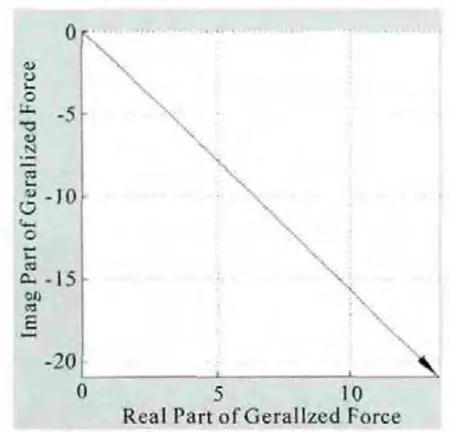
图8 可调导叶势流激励状态下的模态激励因子

5 结论

利用非线性谐波法以及插值程序，把已有的气动计算方法和强度计算方法结合起来，为转静干涉中的尾流激振和势流扰动产生的强迫响应建立了适用于工程设计的、合理的流固耦合计算模型及研究流程。

（1）非线性谐波法可以有效计算转静干涉导致的势流扰动和尾流激振脉动压力，精度和计算效率能达到工程要求，比定常和非定常计算有有一定的优势。

（2）对于强迫响应分析，结合强迫响应计算的应力和模态激励因子，可以对这种势流扰动或尾流激振诱发的强迫响应作出相应评估。

（3）随着经验的积累，模态激励因子可以单独作为评估参数，并可以在完成气动设计后对这种转静干涉进行评估，迅速地回馈气动设计，减少设计流程和时间，而且可以避免引入阻尼比的误差，提高工程上评估这种高周疲劳的精度和效率。

[1] Sander A J,Fleeter S.Blading response to potential field interactions in axial and radial flow turbomachinery[J].Journal of Propulsion and Power，1998，14（2）：199-207.

[2] Lee Y T,Feng J Z.Potential and viscous interactions for a multiblade row compressor[C]//ASME Turbo Expo 2003，Collocated with the 2003 International Joint Power Generation Conference,USA:American Society of Mechanical Engineers，2003.

[3] Bjorn Laumert，HansMartensson.Investigation of unsteady aerodynamic blade excitation mechanisms in a transonic turbine stage,Part I:phenomenological identification and classification[J].Journal of Turbomachinery，2002，124（3）：410-418.

[4] Wei Ning，StuartM.Blade forced response prediction for industrial gas turbines—Part2:verification and application[C]//ASME Turbo Expo 2003,Collocated with the 2003 International Joint Power Generation Conference，USA:American Society ofMechanical Engineers，2003.

[5] 王梅，江和甫，吕文林.在尾流激振情况下叶片振动应力预估技术[J].航空动力学报，2007，22（4）：608-613.WANG Mei，JIANG Hefu，LV Wenglin.Method to predict the blade vibration stress induced by wake flow[J].Journal of Aerospace Power，2007，22（4）：608-613.(in Chinese)

[6] 孟越，李琳，李其汉.尾流激振情况下叶片强迫响应瞬态分析方法[J].北京航空航天大学学报，2006，32（6）：671-674.MENG Yue，LI Lin，LI Qihan.Transient analytical method of vane forcing response under stator-rotorwake influence[J].Journal of Beijing University of Aeronautics and Astronautics，2006，32（6）：671-674.(in Chinese)

[7] 孟越，李琳，李其汉.不对称静子尾迹流场激振力分析及计算方法[J].北京航空航天大学学报，2007，33（9）：1005-1008.MENG Yue，LI Lin，LIQihan.Investigation of force under asymmetry statorwake[J].Journal of Beijing University of Aeronautics and Astronautics，2007，33（9）：1005-1008.(in Chinese)

[8] 李润泽，李琳.跨声速工况下流体诱发叶片振动研究[J].航空动力学报，2008，23（4）：747-753.LIRunze，LI Lin.An investigation of flow induced blade vibrations at the transonic operating condition[J].Journal of Aerospace Power，2008，23（4）：747-753.(in Chinese)

[9] Du Pengcheng，Ning Fangfei.Application of the harmonic balance method in simulating almost periodic turbomachinery flows[R].ASME 2014-GT-25457.

[10] Ning F,Xu L.Numerical investigation of transonic compressor rotor flow using an implicit 3D flow solver with one-equation spalart-all maras turbulence model[R].ASME 2001-GT-0359.

[11] Ning F.MAP：a CFD package for turbomachinery flow simulation and aerodynamic design optimization[R].ASME 2014-GT-26515.

[12] He L.Harmonic solution of unsteady flow around blades with separation[J].AIAA Journal，2008，46（6）：1299-1307.

[13] Vilmin S，Hirsh C，Lorrain E.Unsteady flow modeling across therotor/stator interface using the nonlinear harmonic method[R].ASME-2006-GT-90210.

[14] Li Lin，Wang Peiyi.Evaluation of high-order resonance of blade underwake excitation[R].ASME 2010-GT-23148.