无砟轨道约束对高铁FPS隔震简支梁桥纵向地震反应的影响
黄宇辰,王军文,王少君
(1.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄050043;2.石家庄铁道大学土木工程学院,河北 石家庄050043;3.石家庄铁道大学 机械工程学院,河北 石家庄050043)
无砟轨道约束对高铁FPS隔震简支梁桥纵向地震反应的影响
黄宇辰1,2,王军文1,2,王少君3
(1.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄050043;2.石家庄铁道大学土木工程学院,河北 石家庄050043;3.石家庄铁道大学 机械工程学院,河北 石家庄050043)
以一典型5跨FPS隔震简支梁桥为对象,建立基于两种常用无砟轨道的线桥一体化模型,探讨两种无砟轨道约束对简支梁桥纵向地震反应的影响;并针对CRTSⅡ型板式无砟轨道,研究剪力齿槽刚度、滑动层摩擦系数对简支梁桥纵向地震反应的影响规律。研究结果表明:无砟轨道约束会降低简支梁桥的支座最大纵向位移、支座纵向耗能和最大墩顶纵向位移;与CRTSⅠ型板式无砟轨道相比,CRTSⅡ型板式无砟轨道能降低结构的最大墩顶纵向位移,并对线路起到隔震作用,应优先在 FPS减隔震设计中采用,设计时需合理选择剪力齿槽刚度,并考虑滑动层性能变化对结构纵向地震反应的影响。
地震反应 高铁 简支梁桥 无砟轨道 FPS 减隔震
现行铁路桥梁抗震设计规范推荐在高烈度地震区有条件时采用减隔震设计。FPS(Friction Pendulum System)是一种新型减隔震支座,拥有优越的隔震特性和出色的自复位能力,已经在沪昆客运专线长沙至昆明段山岭坡大桥等工程上得到应用。
目前对铁路FPS减隔震桥梁的地震响应已进行了一些基础研究。其中,夏修身等[1]的分析表明高速铁路多跨简支梁桥FPS的隔震效果显著,但研究并没有考虑线路的约束作用;Iemura等[2]根据试验和理论分析发现线路约束对隔震装置的耗能有一定影响,铁路桥梁不能忽略线路的约束作用。谢旭等[3]的研究表明线路约束对桥梁纵向地震位移和FPS变形有较大影响,但分析模型以道床阻力为线路阻力,仅适用于扣件阻力大于道床阻力的有砟轨道。国内还未见无砟轨道约束对隔震桥梁地震反应影响的研究成果,特别是现今应用广泛的CRTSⅡ型板式无砟轨道(以下简称Ⅱ型板),其道床板纵向连接为整体,板与桥面之间采用“两布一膜”和“剪力齿槽”的设计,对隔震桥梁地震反应的影响也更为复杂。
本文以高铁 FPS隔震简支梁桥为对象,利用OpenSees地震仿真模拟平台,建立线路—桥梁一体化模型,对采用CRTSⅠ型板式无砟轨道(以下简称Ⅰ型板)和Ⅱ型板两种无砟轨道的高速铁路FPS隔震简支梁进行弹塑性地震反应分析,探讨两种无砟轨道约束对FPS隔震桥梁地震反应的影响,为高铁减隔震桥梁的抗震设计提供参考。
1 计算模型
1.1 FPS计算模型及参数
FPS采用考虑修正库伦摩擦系数的双向耦合模型,支座的受力为
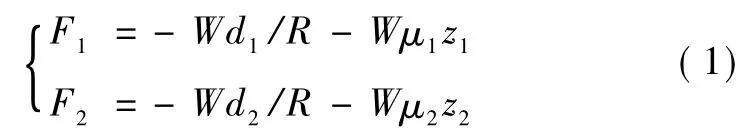
式中:di,Ri,μi分别为支座在桥梁 i轴(i=1(纵轴),i=2(横轴))方向的相对位移、曲率半径、修正库伦摩擦系数;W为支座所受竖向力;z1,z2是反映支座运动状态、摩擦力方向和双向耦合作用的内部滞回分量[4],与支座屈服刚度 Ki=μiW/Y有关,其中,Y表示在将要滑动前支座产生的弹性剪切变形,一般取0.5 mm。FPS支座参数取值如表1所示。其中:fmax,fmin分别是滑块滑动速度较高时与滑块滑动速度为0时的支座摩擦系数;r为控制支座摩擦系数与滑块滑动速度之间关系的参数。
1.2 Ⅱ型板计算模型及参数
Ⅱ型板主要由钢轨、扣件、轨道板、CA砂浆层、底座板、侧向挡块、滑动层等组成,轨道板和底座板跨越
梁缝纵连,梁端轨道板和底座板之间设置剪切钢筋,梁端桥面上设置高强挤塑板,每跨梁固定支座上方设置剪力齿槽,路基过渡段设置摩擦板传力体系和端刺锚固体系。计算模型如图1所示。

表1 FPS初始参数
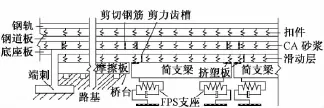
图1 Ⅱ型板计算模型
采用WJ-8C小阻力扣件,每组扣件竖向刚度取60 MN/m;横向刚度取30 MN/m;扣件纵向阻力在无载时取13 kN/m/轨,塑性非线性临界点为0.5 mm。
CA砂浆层纵、横向刚度为128 MN/m,塑性非线性临界点为0.5 mm;竖向抗压刚度取2×106MN/m;考虑现场施工质量难以保证,CA砂浆与混凝土粘结面极限抗拉强度为0.1 MPa,经计算得竖向抗拉刚度为5.93×105MN/m,弹性非线性临界点为4.3×10-7m。
侧向挡块为全D型挡块布置,桥梁加路基过渡段每8 m布置一对;单个挡块在横向限制道床板的横向位移,视为刚性连接;竖向抗拉刚度为620 MN/m。
滑动层由两布一膜组成,滑动层不能承受拉力,根据试验[5],单位长度的竖向抗压刚度取 1.5×103MN/m;其纵、横向阻力为摩擦阻力,摩擦系数取0.2,摩擦屈服变形为0.5 mm。
剪力齿槽设14根直径为28 mm的HRB335剪力钉,剪力钉高度为120 mm,锚固板厚度为28 mm,考虑剪力钉滑移效应,计算得单根剪力钉线性剪切刚度为67 MN/m,开始滑移点为1.9 mm,滑移荷载为127 kN,极限滑移值为11.76 mm;剪力齿槽竖向刚度为2.296 ×104MN/m。
轨道板剪切钢筋分别在梁缝两侧布置8根、端刺和路基过渡两侧布置32根直径28 mm的HRB500钢筋,单根剪切钢筋纵、横向刚度为300 MN/m;竖向刚度为2×103MN/m。
高强挤塑板不能承受拉力。据规范可计算得1.45 m长挤塑板最小竖向抗压刚度为600 MN/m,本文取600 MN/m。
摩擦板以小端刺固结在路基上,板上设置两层土工布,不能承受拉力,其竖向抗压刚度取 1×106MN/m;摩擦系数取0.7,摩擦屈服变形为0.5 mm。大端刺与底座板相连,固结在路基上,不考虑其变形。
1.3 Ⅰ型板计算模型及参数
Ⅰ型板主要由钢轨、扣件、轨道板、CA砂浆、底座板、凸形挡台、树脂填充层等组成。底座板分块布置,在梁缝处断开;梁面与底座板采用预埋套筒植筋连接,底座板上设置凸形挡台限制轨道板的纵、横向位移,因此将轨道板和底座板看成一个整体道床板固结在梁面上。由于扣件纵向阻力远小于道床阻力,所以线路阻力只考虑扣件阻力。计算模型如图2所示。

图2 Ⅰ型板计算模型
钢轨、道床板的材料和截面特性等均按实际取值,扣件一般采用WJ-7B型小阻力扣件,每组扣件竖向刚度取为50 MN/m,横向刚度取30 MN/m,扣件纵向阻力在无载时同样取13 kN/m/轨。
1.4 基于OpenSees的有限元分析模型
选取某5跨高速铁路FPS隔震规则简支梁桥,跨径为32 m,主梁采用C55混凝土,梁体每端布置2个FPS支座,墩柱采用C40混凝土,桥墩为圆端形重力式墩,墩高15 m,墩底与地面固结。为消除边界效应,桥两端各伸出50 m路基过渡段并考虑轨道锁定点,分别铺设Ⅱ型和Ⅰ型板式无砟轨道。图3为有限元计算模型。其中钢轨、道床板、主梁、桥墩均用弹性梁柱单元模拟,各层间连接用零长连接单元模拟,滑动层用接触摩擦单元模拟,剪力齿槽用生死单元模拟;摩擦板和端刺固结在路基上,不考虑邻梁间碰撞效应;FPS支座与主梁、桥墩采用刚臂连接,假设在地震作用下 FPS限位板剪断,且梁体位移在支座设计最大位移之内。
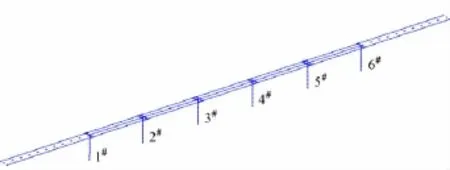
图3 简支梁有限元模型
2 地震波的选取
从PEER地震数据库选取9条地震波(表2),将各波加速度峰值统一调整为0.4g。地震波数据中按
照美国USGS规定的场地类别划分为B类、C类和D类,分别对应于我国《公路桥梁抗震设计细则》中的Ⅰ(Ⅱ)类、Ⅲ类、Ⅳ类场地类别。
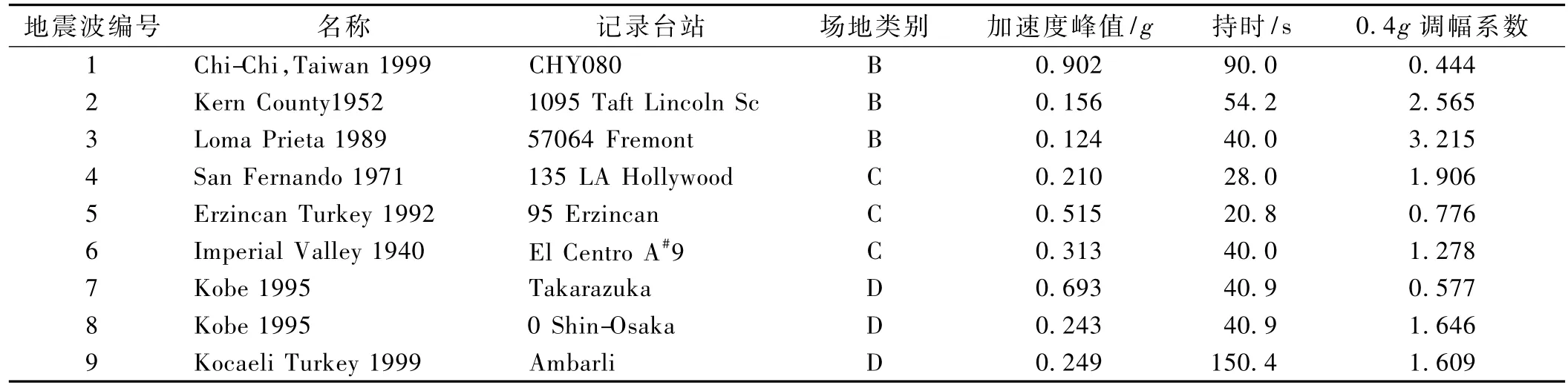
表2 选取的地震波
3 无砟轨道约束对结构动力特性和纵向地震反应的影响
3.1 无砟轨道约束对结构动力特性的影响
结构动力特性研究是分析结构地震反应的基础。为研究无砟轨道约束对高铁 FPS隔震简支梁桥动力特性的影响,分3种工况取结构前10阶模态(质量参与系数>90%)进行分析。工况1:考虑Ⅰ型板的轨道约束作用;工况2:考虑Ⅱ型板的轨道约束作用;工况3:不考虑轨道约束作用。图4为考虑无砟轨道约束时与忽略轨道约束时结构自振频率之比随自振模态阶数的变化规律。
由图4可见,无砟轨道约束增大了结构各阶振型的自振频率,其中工况2的增大幅度要高于工况1,两工况的增大幅度都在低阶模态时更大,而后增大幅度变小,并慢慢趋于稳定。

图4 无砟轨道约束对结构动力特性的影响
3.2 无砟轨道约束对结构纵向地震反应的影响
为研究无砟轨道约束对高铁 FPS隔震简支梁桥的纵向地震反应影响,分别对3种工况在纵向输入9条地震波(表2),分场地类别取中跨结构的纵向地震反应均值。图5至图7分别给出了3种工况下中跨的支座最大纵向位移、4#墩最大墩顶纵向位移和最大墩底纵向剪力。
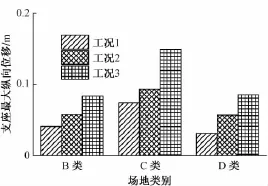
图5 支座最大纵向位移

图6 4#墩最大墩顶纵向位移

图7 4#墩最大墩底纵向剪力
由图5至图7可见,与工况3相比,3类场地波作用下工况1和工况2的支座最大纵向位移和4#墩最大墩顶纵向位移均不同程度地降低,4#墩最大墩底纵向剪力则变化不大;其中C类场地波作用下的反应降低幅度较B,D类场地波大。
3.3 Ⅱ型板和Ⅰ型板的结构纵向地震反应对比
由图5至图7可见,3类场地波作用下工况2的支座最大纵向位移要高于工况1,最大提高83%,4#墩最大墩顶纵向位移要低于工况1,最大降低31%,4#墩最大墩底纵向剪力则与工况1相差不大。
图8为3类场地波作用下工况1、工况2中跨结构的最大扣件纵向变形。由图8可见:工况2的扣件最大纵向变形很小,都在弹性范围内;而工况1的扣件已经进入塑性,最大塑性变形达9.2 cm。
为了研究上述反应差异的主要原因,本文以6号地震波作用下中跨4#墩某一FPS滞回曲线以及相应
累积耗能为对象进行分析。定义累积耗能为地震持续时间t内FPS支座和其上方半跨范围内单线线路约束的纵向滞回曲线所包围的面积和。其计算公式为

式中:F1,d1分别为FPS支座的纵向力和纵向位移;Fu, du分别为相应线路约束的纵向约束力和纵向位移。
其中工况1的线路约束耗能主要为扣件纵向塑性变形耗能,工况2的线路约束耗能主要为滑动层的纵向摩擦耗能以及剪力齿槽的塑性变形耗能。图9、图10分别给出了3种工况下中跨4#墩某一FPS支座的纵向滞回曲线以及相应的累积耗能曲线。
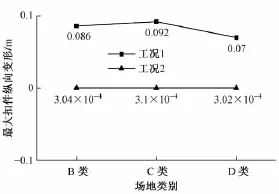
图8 最大扣件纵向变形
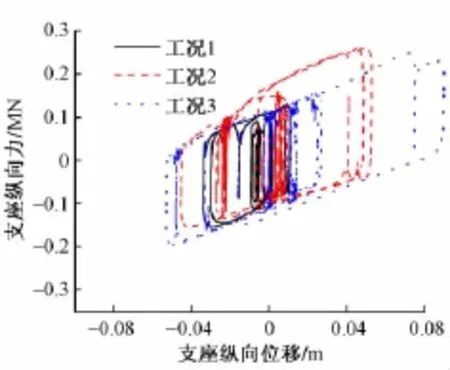
图9 FPS支座的纵向滞回曲线

图10 结构的累积耗能曲线
图9、图10显示:无砟轨道约束降低了高铁FPS隔震简支梁桥的支座最大纵向位移和支座纵向耗能,并使最大墩顶位移减小;与Ⅰ型板相比,Ⅱ型板约束增大了结构的支座最大纵向位移,降低了结构的最大墩顶纵向位移,减小了扣件最大纵向变形,最大墩底纵向剪力则变化不大。
4 Ⅱ型板约束参数对FPS隔震简支梁桥纵向地震反应的影响
4.1 滑动层摩擦系数的影响
滑动层摩擦系数决定底座板与梁面之间的纵向阻力,其性能受环境、使用时间等因素的影响,使摩擦系数会有较大改变。为研究滑动层摩擦系数对高铁FPS隔震简支梁桥纵向地震反应的影响,假设滑动层摩擦系数分别为0.1,0.2,0.3,0.4,0.5,保持模型其他参数不变,输入9条地震波(表2),对结构纵向地震反应进行分析,分场地类别取中跨结构的纵向地震反应均值;得出3类场地波作用下中跨结构的支座最大纵向位移、4#墩最大墩顶纵向位移和最大墩底纵向剪力如图11所示,最大扣件纵向变形如图 12所示。由图11、图12可见,随着滑动层摩擦系数的增大,3类场地波作用下中跨结构的支座最大纵向位移和4#墩最大墩顶纵向位移均减少,4#墩最大墩底纵向剪力、最大扣件纵向变形则变化不大。其中,支座最大纵向位移和4#墩最大墩顶纵向位移在摩擦系数从0.1增大到0.3时,降幅较大,而后降幅变小,并慢慢趋于稳定。因此,在高铁桥FPS减隔震设计时,应考虑滑动层性能随时间和环境的变化(如滑动层吸水造成其摩擦系数大幅下降[6]等)对结构纵向地震反应的影响。
4.2 剪力齿槽刚度的影响
为研究剪力齿槽刚度对FPS隔震简支梁桥纵向地震反应的影响,假设剪力齿槽剪力钉根数分别为10,14,18,22,26根,保持模型其他参数不变,输入9条地震波(表2),分场地类别取中跨结构的纵向地震反应均值;得出3类场地波作用下中跨的最大扣件纵向变形如图13所示,支座最大纵向位移、4#墩最大墩顶纵向位移和最大墩底纵向剪力如图14所示。

图11 滑动层摩擦系数对结构纵向地震反应的影响
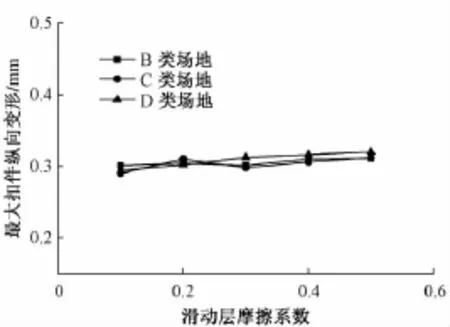
图12 滑动层摩擦系数对最大扣件纵向变形的影响

图13 剪力齿槽刚度对最大扣件纵向变形的影响

图14 剪力齿槽刚度对结构纵向地震反应的影响
由图13、图14可见,随着剪力钉根数的增多,3类场地波作用下中跨结构的最大扣件纵向变形逐渐增大,支座最大纵向位移、4#墩最大墩顶纵向位移、最大墩底纵向剪力都有先减少后增大的趋势。因此,在设计时,考虑结构纵向地震反应和扣件纵向变形的变化的同时,剪力齿槽刚度不宜太小也不能过大,对于本算例,剪力钉根数取18根左右较为合适。
5 结论
1)无砟轨道约束作用会降低 FPS隔震简支梁桥结构的支座最大纵向位移、支座纵向耗能和最大墩顶纵向位移,最大墩底纵向剪力则变化不大。
2)与Ⅰ型板相比,Ⅱ型板能降低FPS隔震简支梁桥的最大墩顶纵向位移,增大 FPS支座最大纵向位移,并对线路起到隔震作用;因此,相对于扣件阻力小于道床阻力的无砟轨道,在避免发生邻梁间碰撞时,Ⅱ型板更适合高铁简支梁桥的FPS减隔震设计。
3)随着Ⅱ型板滑动层摩擦系数的增大,结构支座最大纵向位移和最大墩顶纵向位移均减少,而最大墩底纵向剪力和最大扣件纵向变形则变化不大。在设计时,应考虑滑动层性能随时间和环境变化对结构纵向地震反应产生的不利影响。
4)随着Ⅱ型板剪力齿槽刚度的增大,最大扣件纵向变形逐渐增大,结构支座最大纵向位移、最大墩顶纵向位移和最大墩底纵向剪力均有先减小后增大的趋势。在满足无砟轨道纵向力的有效传递的前提下,设计中选择合理的剪力齿槽刚度。
[1]夏修身,赵会东,欧阳辉来.高速铁路桥梁基于摩擦摆支座的减隔震研究[J].工程抗震与加固改造,2014,36(3):21-27.
[2]IEMURA H,IWATA S,MURATA K.Shake Table Tests and Numerical Modeling of Seismically Isolated Railway Bridges[C]//Proceedings of the 13thWorld Conference on Earthquake Engineering.Vancouver:Canadian Association for Earthquake Engineering,2004.
[3]谢旭,王炎,陈列.轨道约束对铁路减隔震桥梁地震响应的影响[J].铁道学报,2012,34(6):75-83.
[4]焦驰宇,胡世德,管仲国.FPS抗震支座分析模型的比较研究[J].振动与冲击,2007,26(10):113-117.
[5]吴斌,陈文荣,刘参,等.列车竖向荷载下CRTSⅡ型板式无砟轨道结构受力特性试验研究[J].铁道科学与工程学报,2014,11(3):37-44.
[6]赵体波,牛斌,胡所亭,等.CRTSⅡ型板式无砟轨道滑动层性能试验研究[J].施工技术,2011,40(9):45-48.
(责任审编 孟庆伶)
U441+.7
:ADOI:10.3969/j.issn.1003-1995.2015.09.08
2015-05-10;
:2015-06-29
河北省自然科学基金项目(E2015210038)
黄宇辰(1992— ),男,江西抚州人,硕士研究生。
1003-1995(2015)09-0024-05

