污染监测视电阻率快速三维反演成像
崔益安 ,朱肖雄 ,陈志学 ,柳建新
(1. 中南大学 地球科学与信息物理学院, 长沙 410083; 2. 中南大学 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083)
随着我国经济的持续高速发展,在工业化、城镇化过程中的环境污染问题也日益严重。特别是越来越多的工矿废水废渣库、生活和工业垃圾填埋场等,严重威胁周边的土壤与地下水安全[1],即时检测和控制污染源扩散是保护土壤和地下水不受污染或少受污染的积极方法[2]。与钻孔测试、定期采样分析等传统环境监测手段相比,直流电阻率法等地球物理方法具有效率高、成本低、快速无损、无二次污染等优点[3], 在地下污染探测的应用中有较强的优势。王迪等[4]就采用电阻率成像法对北京某垃圾场进行了污染探测,取得不错的效果;VAUDELET 等[5]也采用电阻率法成功地在城市地区实现对污染物的成像。类似的研究与应用还有很多[6-9]。随着污染控制与治理的进一步需求,电阻率法在污染物探测的应用中正逐步由二维观测向三维观测发展,同时也由短时单次观测向长期连续监测发展,如尚浩等[10]和郭秀军等[11]研制开发了三维分布式监测系统用于垃圾填埋场渗漏的监测;GASPERIKOVA 等[12]采用电阻率法对地下污染活动进行长期监测。在这些电阻率法污染监测的应用中,即便是采用了三维观测,但其观测数据的反演解释还是基本以二维处理为主[4,10]。污染监测数据的反演解译至关重要,只有开展三维反演才能满足污染监测中的高精度数据处理要求。
因此,有必要针对直流电阻率法在地下污染监测中的应用开展监测数据的快速三维反演算法研究,以满足实际应用中对数据解译的精确性和时效性要求。正演模拟是反演计算的基础,潘克家等[13]采用多重网格法以及黄俊革等[14]采用有限单元法进行了直流电阻率法正演模拟,获得较高的模拟精度,但这类正演方法计算量巨大,比较耗时。ZHANG 等[15]采用模拟阻抗网络开展直流电阻率法正演模拟研究,获得的阻抗刚度矩阵除对角元素和次对角元素外全为0,求解简便,便于提高正演计算速度。许多研究人员在直流电阻率反演方面开展了大量研究。戴前伟等[16]将智能优化方法应用到电阻率层析成像的反演计算中。LI 等[17]和刘斌等[18]研究了通过约束来提高三维电阻率反演收敛速度的方法。但这些反演方法普遍耗时较长,不适合污染监测数据实时快速解译的需求。梯度法是基于求偏导数来寻找极值点,是一类迭代次数少、收敛快的反演方法。吴小平等[19]采用共轭梯度法开展电阻率三维反演研究,计算速度较快,取得不错的反演效果。黄俊革等[20]更是针对坑道超前探测专门研究了直流电阻率的快速反演方法。污染监测数据同样需要实时快速解译以便及时提供决策依据,因此,本文作者开展相关研究,在采用模拟阻抗网络进行正演模拟提高计算速度的基础上,通过共轭梯度快速迭代来实现对污染监测电阻率数据的快速三维反演。
1 模拟阻抗网络模型
正演模型是开展反演研究的基础。一般情况下,大地介质中的直流电阻率法问题满足式(1)
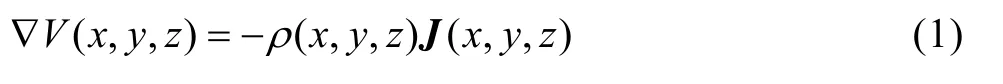
正演计算的目的是通过给定介质的三维电阻率分布ρ(x,y,z)以及电流密度J(x,y,z)来计算空间中的电势分布V(x,y,z)。计算过程中需要先将模型离散化,然后进行求解。图1 所示为模拟阻抗网络模型。由图1 可知,模拟阻抗网络模型将地电模型分割成许多六面体电阻块,每个块在x、y、z 3 个方向的长度分别为 Δx 、Δz 。把空间电势分布与电流密度分布均定义在每个块的顶面中心点,称之为网络节点。除边界外,每个节点在三维空间中都有6 个相邻的节点通过阻抗臂与之连接,每条阻抗臂的阻抗由所在块的电阻率以及节点之间的距离决定。
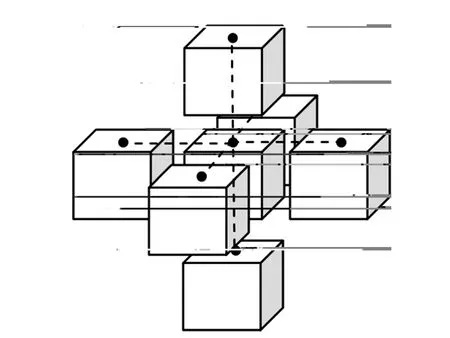
图1 模拟阻抗网络模型 Fig. 1 Model of analogy impedances network
如将图1 中的中心立方块在空间中的位置定义为(i, j, k),电阻率为ρ(i, j, k),其网络节点电压为V(i, j, k),则节点(i, j, k)与节点(i-1, j, k)之间阻抗臂的阻抗Rx为
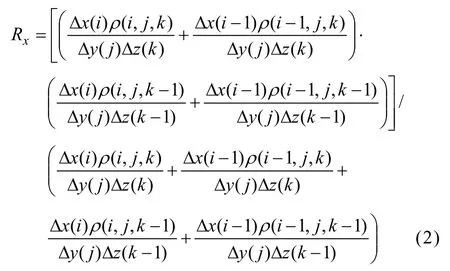
节点(i, j, k)与节点(i, j-1, k)之间阻抗臂的阻抗Ry为
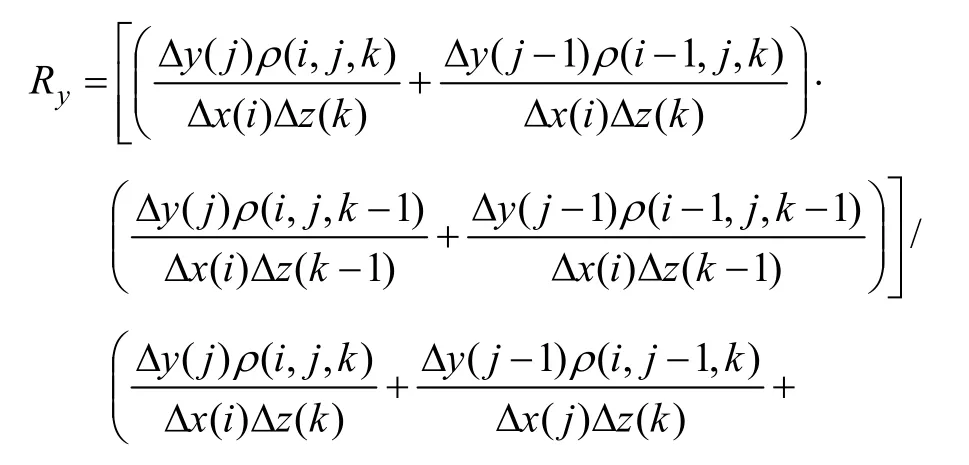
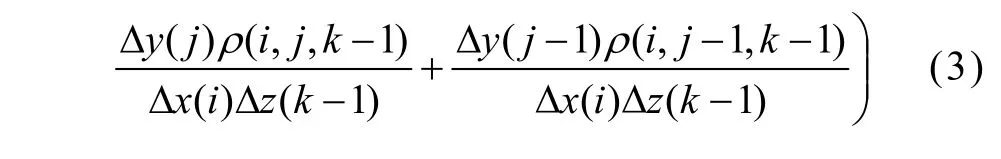
节点(i, j, k)与节点(i, j, k-1)之间阻抗臂的阻抗Rz为

为满足纽曼边界条件(n·j=0),处于地表的节点没有与空气相连的阻抗臂,地下边界节点的设置则需要满足第一类边界条件。由于空间中各节点的电势与电流均满足基尔霍夫定律,将式(1)中电势梯度用模拟电阻网络中相邻节点的电势差分代替后有

式中:K 为表示阻抗分布结构的刚度矩阵。矩阵K 的对角元素为与其对应节点相连的所有电导之和,次对角元素为对应节点与相连节点之间的负电导,其他元素均为0。通过式(5)求解便可以获得各节点的电势 V(x, y, z),即实现正演模拟。
2 共轭梯度反演算法
算数据f(m)之间的残差; mΔ 为每次迭代的模型增量。
有许多方法可以用来求解迭代方程(9),其中许多方法均需要完全计算灵敏度矩阵。而在采用共轭梯度的迭代法中,只需要计算灵敏度矩阵A 或其转置矩阵与一个向量X 的乘积结果,因为不用完全计算灵敏度矩阵,大大节约了计算时间和存储空间,如式(10)所示:
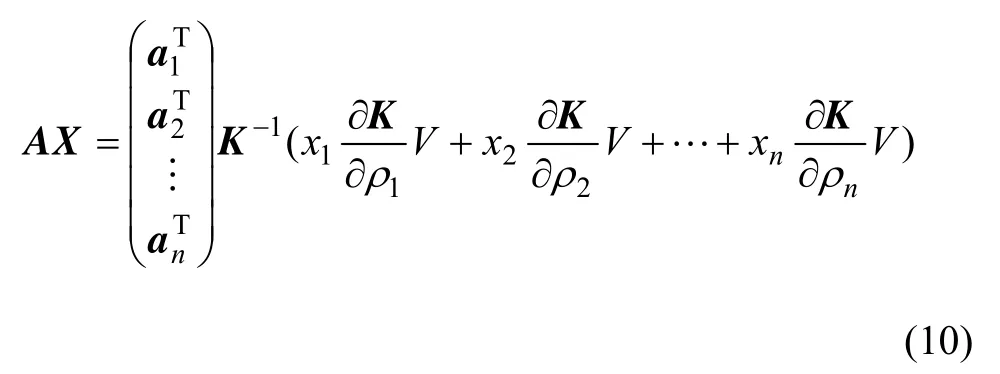
反演就是通过一定的策略来估计符合要求的模型参数。令模拟电阻网络离散化后的地电模型 m= (ρ1, ρ2, …, ρi×j×k)T,对于存在n 个视电阻率观测数据dob=(ρs1, ρs2, …, ρsn)T,反演问题即为寻找适当的模型m 以满足
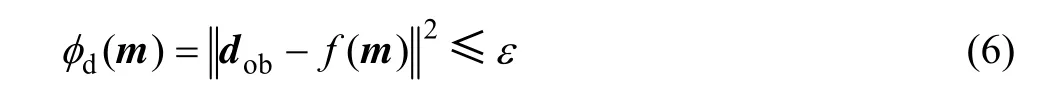
采用共轭梯度法快速反演的具体迭代算法如下:
1) 设定最大反演和共轭梯度迭代次数imax和jmax,设定允许的拟合差ε,给定初始模型m0与参考模型m0;
3) 如果 idΔ ≤ε 则跳转到8);
4) 计算 bi= ATΔdi;
5) 共轭梯度循环for j=1 to jmax:
式中:f(m)为模型m 的正演计算数据;ε 为允许的拟合差。由于正演模型与实际物理模型的差异以及观测数据的噪音影响等因素,这类问题往往没有确定解或存在多解。地球物理反演问题的不适定性在引入Tikhonov 正则化后,可以得到适当的改善,求解稳 定[21],如式(7)所示:


最终,可以获得反演问题的最小二乘迭代计算方程,如式(9)所示:
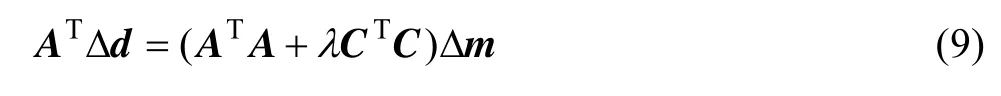
式中:A 为灵敏度矩阵; dΔ 为观测数据dob与正演计
4月26日上午,十一届全国人大常委会第二十六次会议在人民大会堂举行联组会议,专题询问国务院关于农田水利建设工作情况。受国务院委托,水利部、发展改革委、财政部、国土资源部、农业部、银监会等六部委负责人到会听取意见,回答询问(本期“特别关注”全文刊发)。这是全国人大常委会2012年举行的第一次专题询问。受吴邦国委员长委托,乌云其木格副委员长主持会议。
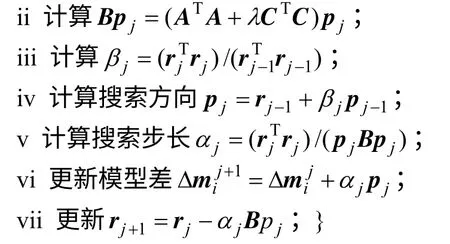
7) 如没有达到最大反演次数imax则跳转到2);
8) 反演结束。
3 计算模拟与实验测试
3.1 模拟数据测试
首先采用模拟合成数据对反演算法进行了测试。设三维模型xy 平面由8×10 个网格组成,z 方向为深度分8层,共计640 个网格,每个网格尺寸均为1.1 m×1.1 m×0.46 m。图2(a)所示为模拟数据模型1。模型1 的第1 层x 与y 方向的第1、2 网格电阻率为10 Ω·m,其余网格电阻率均为200 Ω·m,低阻网格用来模拟地表存在的污染源。图2(b)所示为模拟数据模型2。模型2 的第1 层与第2 层x 方向第1、2 网格以及y 方向的第1、2、3 网格电阻率为10 Ω·m,模拟地表污染扩散至这些区域,其余网格电阻率为200 Ω·m。
设视电阻率观测采用二极装置,电极在地表xy平面布置,共布置5×6 个电极,电极距为2.1 m。然后,利用模拟阻抗网络数值方法进行正演模拟,计算出各电极点位置的二级装置电压与供电电流的比值。利用计算获得的模拟观测数据对三维反演算法进行测试。由于采用模拟阻抗网络进行正演模拟以及采用共轭梯度反演算法,网格内无需插值,反演计算时间复杂度为一阶o(n),耗时较少,640 个网格的计算在普通个人计算机上(intel 2.1 GHz CPU)上的计算耗时仅为采用有限单元法耗时的一半。图3 所示为反演计算测试结果,图3(a)和(b)分别为模型1 和模型2 模拟数据的反演三维视电阻率结果的水平切片。图3 中只给出了深度分别为0、0.5、0.9、1.4 和1.8 m 共5 个切片,重点研究反演三维视电阻率结果对模型电阻率发生变化区域的响应情况。
反演结果能很好的反映模型1 与模型2 之间的电阻率变化情况,并且对电阻率变化的区域与电阻率数值大小均有比较精确的响应,表明该反演方法可以有效实现对直流电阻率数据的快速三维反演成像计算。
3.2 实测数据反演
为进一步验证反演方法的有效性,还开展了实测数据的计算测试。实测数据来自某场地进行盐水注射过程中的视电阻率监测实验。实验在钻孔中注入高浓度的盐水来模拟污染物在地下介质中的扩散情况。视电阻率监测采用AGI 公司生产的Sting R1 型电法仪器,通过自动电极转换器同时布置30 个电极,开展二极装置视电阻率成像观测。试验场地监测区域大小约为10 m×12 m。图4 所示为视电阻率监测电极布置。x 和y 方向电极距均为2.1 m。二级装置的一个供电电极和一个测量电极均布置在远离监测区域的“无穷远”处,图4 中的各测点依次供电进行循环扫描观测。
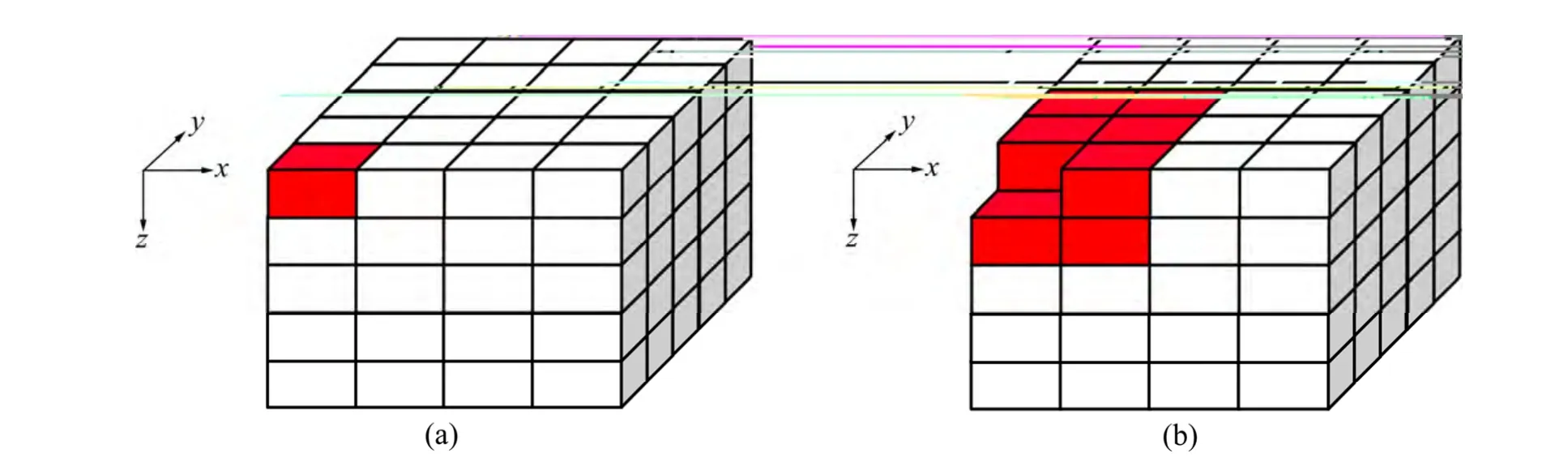
图2 模拟数据模型 Fig.2 Models of synthetic data: (a) Model 1; (b) Model 2
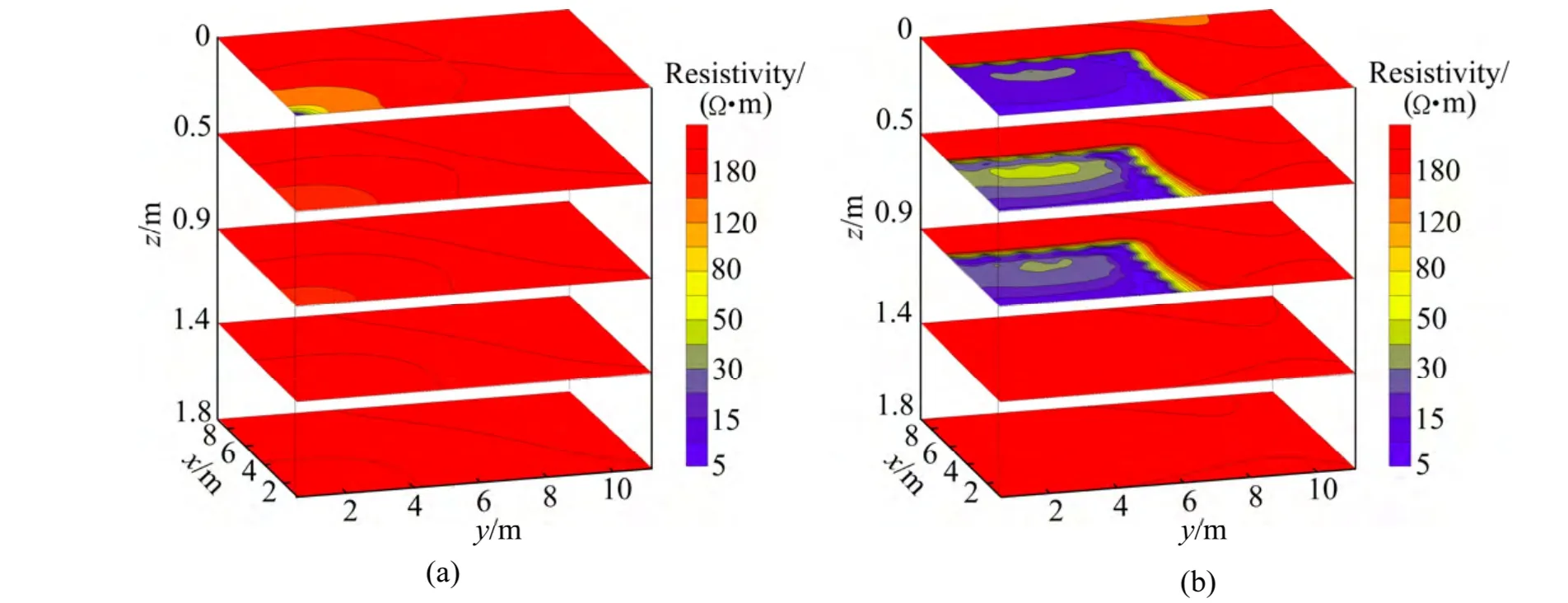
图3 模拟数据反演视电阻率结果 Fig. 3 Results of inversing synthetic resistivity data: (a) Model 1; (b) Model 2
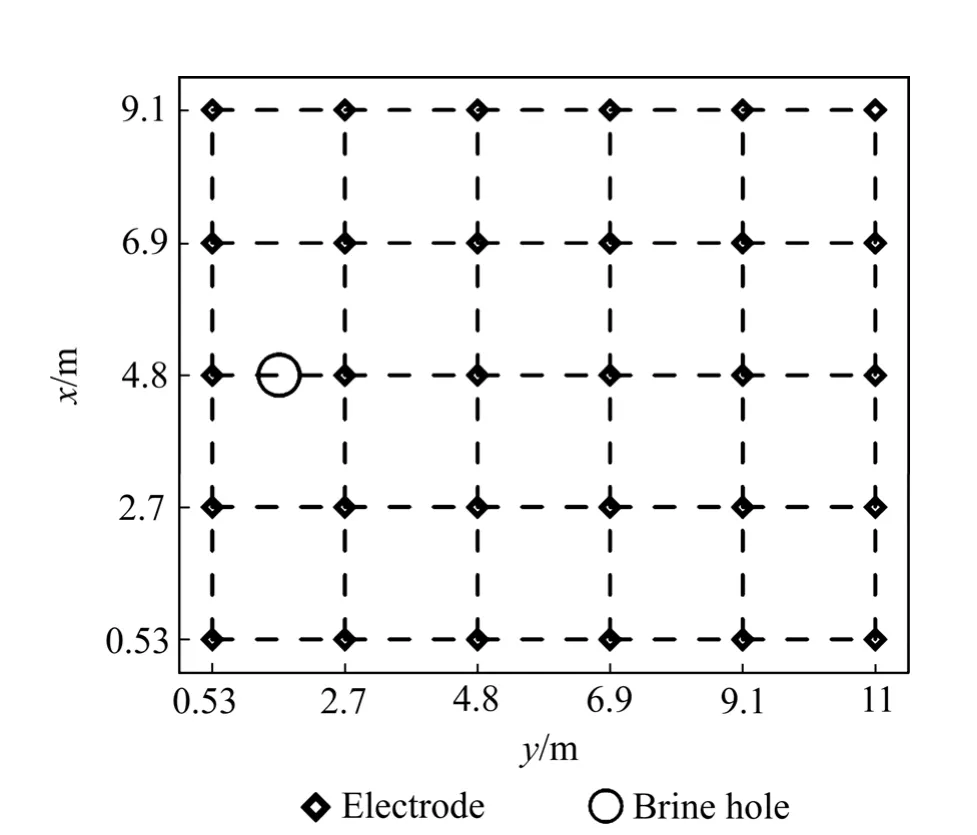
图4 视电阻率监测电极布置 Fig. 4 Survey array of apparent resistivity monitoring
盐水注射孔深度1 m,位于场地一侧2 个电极之间(见图4),在注射盐水前先进行了一次二极法视电阻率扫描观测,然后开始注射盐水。注射盐水后的第2天开始,每天进行一次视电阻率扫描观测,监测用来 模拟污染物的盐水在地下介质中的扩散情况和影响范围。对每次采集到的视电阻率观测数据进行三维反演计算,获得一系列的三维反演成像结果,便可以直观地了解盐水连续扩散的具体情况。图5 所示为3 次不同时间监测数据进行三维反演成像的计算结果。图 5(a)为开始注射盐水前观测数据的三维视电阻率反演结果水平切片,深度分别为0、0.9、1.8、2.7 和3.6 m。反演结果表明该场地浅地表具有较明显的电性分层,表层厚度约1 m 左右电阻率稍高,随着深度增加电阻率逐步降低。图5(b)和(c)分别为注射盐水后第3 天和第6 天观测数据的三维视电阻率反演结果。从图5(b)和(c)中可以明显看出,由于盐水注射导致的低电阻率区域。对比图5(a)~(c)可以很直观地了解盐水在地下的渗透扩散情况,由于盐水渗透扩散引起的低电阻率区域主要沿注射孔底部向四周扩散,并且在水平y 方向的扩散速度高于其他方向的速度。测试表明:反演算法对实际监测数据的反演计算也具有良好的应用效果,可以提供一系列直观的三维视电阻率影像,快捷地实现对污染物视电阻率监测数据的动态实时解译。
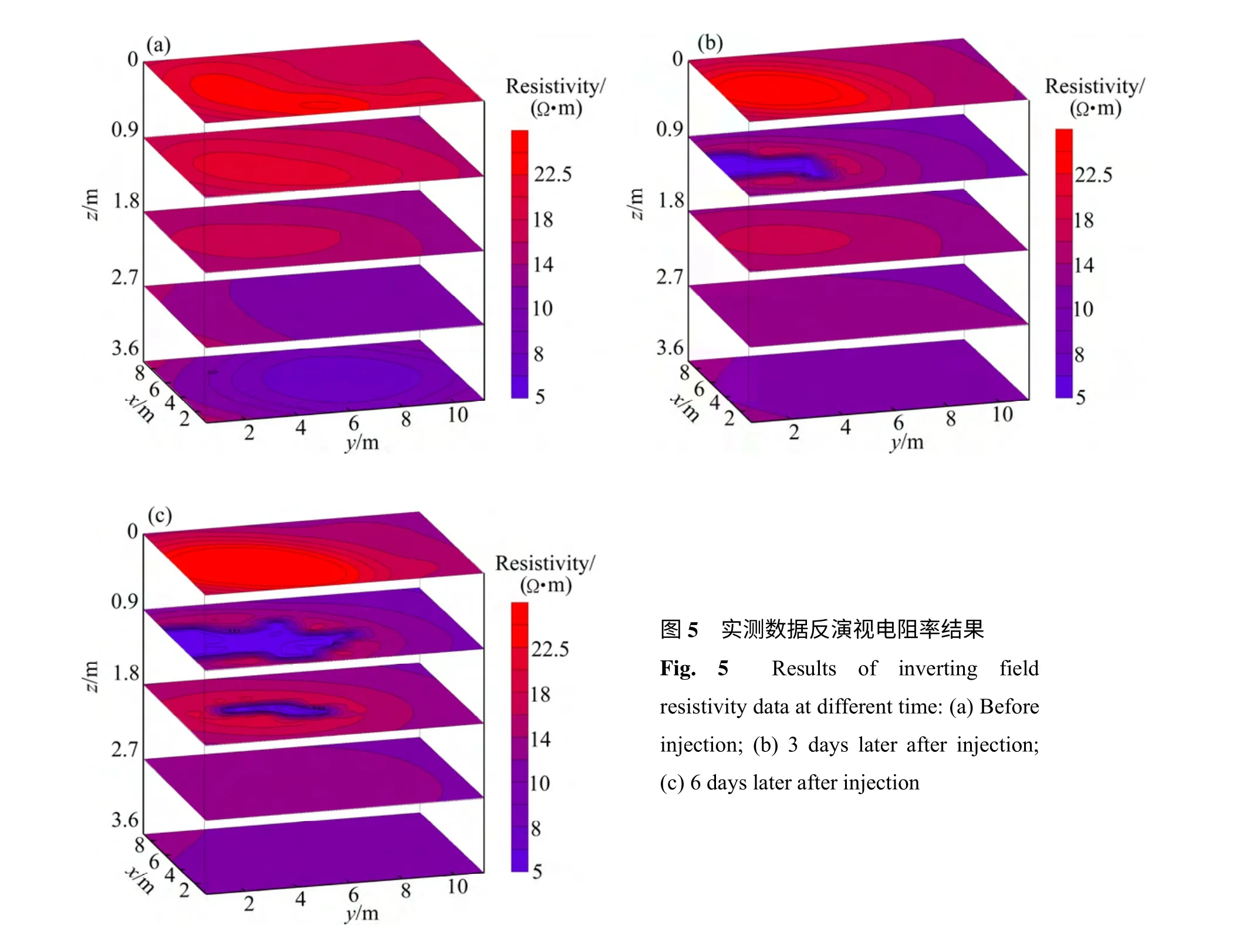
图5 实测数据反演视电阻率结果 Fig. 5 Results of inverting field resistivity data at different time: (a) Before injection; (b) 3 days later after injection; (c) 6 days later after injection
4 结论
1) 视电阻率快速三维反演方法能有效地实现对污染监测数据的快速有效反演,使得三维反演可在普通计算机上短时内完成,有利于提高监测数据解释的时效性。
2) 采用模拟阻抗网络模型对地下污染地电模型进行数值模拟,在保证模拟精度的同时减少正演计算量,为快速反演提供良好的模型基础。
3) 共轭梯度迭代过程中只需要计算灵敏度矩阵或其转置矩阵与向量的乘积,而不用完全计算灵敏度矩阵,大大节约计算时间和存储空间,使得反演算法可以快速实现对监测数据的反演。
4) 针对污染监测视电阻率数据的快速反演方法,能实时直观地提供一系列准确反映地下污染扩散动态范围的三维视电阻率分布,可为地下污染的防控与处理及时提供可靠的依据。
致谢:
感谢刘澜波教授提供场地实验及相关监测数据。
[1] 刘 月, 董颖博, 林 海, 陈月芳, 于明利. 云南某典型锡矿选矿厂重金属污染特征[J]. 中国有色金属学报, 2014, 24(4): 1084-1090. LIU Yue, DONG Ying-bo, LIN Hai, CHEN Yue-fang, YU Ming-li. Pollution characteristics of heavy metals in typical tin mineral processing plant of Yunnan, China[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(4): 1084-1090.
[2] 程业勋, 杨 进, 赵章元. 环境地球物理学的现状与发展[J]. 地球物理学进展, 2007, 22(4): 1364-1369. CHENG Ye-xun, YANG Jin, ZHAO Zhang-yuan. Status and development of environmental geophysics[J]. Progress in Geophysics, 2007, 22(4): 1364-1369.
[3] 郑军卫, 张志强, 董连成. 环境地球物理学及其现状与进展[J]. 地球科学进展, 2000, 15(1): 40-47. ZHENG Jun-wei, ZHANG Zhi-qiang, DONG Lian-cheng. Environmental geophysics and its advance[J]. Advance in Earth sciences, 2000, 15(1): 40-47.
[4] 王 迪, 尉 斌, 闫永利, 马晓冰, 王显祥, 杨京勤, 鲁笑颖. 垃圾填埋场地下环境污染检测方法技术研究[J]. 地球物理学报, 2012, 55(6): 2115-2119. WANG Di, WEI Bin, YAN Yong-Li, MA Xiao-Bing, WANG Xian-xiang, YANG Jing-qin, LU Xiao-ying. Study of detecting technology for landfill underground environmental pollution[J]. Chinese Journal of Geophysics, 2012, 55(6): 2115-2119.
[5] VAUDELET P, SCHMUTZ M, PESSEL M, FRANCESCHI M, GUÉRIN R, ATTEIA O, BLONDEL A, NGOMSEU C, GALAUP S, REJIBA F, BÉGASSAT P. Mapping of contaminant plumes with geo-electrical methods. A case study in urban context[J]. Journal of Applied Geophysics, 2011, 75(4): 738-751.
[6] GALLAS J D F, TAIOLI F, MALAGUTTI FILHO W. Induced polarization, resistivity, and self-potential: A case history of contamination evaluation due to landfill leakage[J]. Environmental Earth Sciences, 2011, 63(2):251-261.
[7] ABDULLAHI N K, OSAZUWA I B. Geophysical imaging of municipal solid waste contaminant pathways[J]. Environmental Earth Sciences, 2011, 62(6): 1173-1181.
[8] METWALY M, KHALIL M A, AL-SAYED E S, EL-KENAWY A. Tracing subsurface oil pollution leakage using 2D electrical resistivity tomography[J]. Arabian Journal of Geosciences, 2013, 6(9): 3527-3533.
[9] OLOWOFELA J A, AKINYEMI O D, OGUNGBE A S. Imaging and detecting underground contaminants in landfill sites using electrical impedance tomography (EIT): A case study of Lagos, southwestern, Nigeria[J]. Research Journal of Environmental and Earth Sciences, 2012, 4(3): 270-281.
[10] 尚 浩, 郭秀军, 王仙丽, 孟庆生. 垃圾填埋场渗漏污染三维分布式电学监测系统研制及应用[J]. 地球物理学进展, 2010, 25(4): 1485-1491. SHANG Hao, GUO Xiu-jun, WANG Xian-li, MENG Qing-sheng. Design and experiment of the 3-D electrical resistivity detecting system for monitoring underground soil contaminated by landfill leachate[J]. Progress in Geophysics, 2010, 25(4): 1485-1491.
[11] 郭秀军, 魏 丽, 贾永刚, 黄潇雨. 垃圾填埋场渗滤液污染地下含水层及修复过程的三维动态监测实验[J]. 地球物理学进展, 2006, 21(2): 637-642. GUO Xiu-jun, WEI Li, JIA Yong-gang, HUANG Xiao-yu. Experiment of monitoring underground aquifers contaminated by leachate of landfill and remation with 3-D electrical method[J]. Progress in Geophysics, 2006, 21(2): 637-642.
[12] GASPERIKOVA E, HUBBARD S S, WATSON D B, BAKER G S, PETERSON J E, KOWALSKY M B, SMITH M, BROOKS S. Long-term electrical resistivity monitoring of recharge-induced contaminant plume behavior[J]. Journal of Contaminant Hydrology, 2012, 142/143(11): 33-49.
[13] 潘克家, 汤井田, 胡宏伶, 陈传淼. 直流电阻率法2.5 维正演的外推瀑布式多重网格法[J]. 地球物理学报, 2012, 55(8): 2769-2778. PAN Ke-jia, TANG Jing-tian, HU Hong-ling, CHEN Chuan-miao. Extrapolation cascadic multigrid method method for 2.5D direct current resistivity modeling[J]. Chinese Journal of Geophysics, 2012, 55(8): 2769-2778.
[14] 黄俊革, 阮百尧, 鲍光淑. 基于有限单元法的三维地电断面电阻率反演[J]. 中南大学学报(自然科学版), 2004, 35(2): 295-299. HUANG Jun-ge, RUAN Bai-yao, BAO Guang-shu. Resistivity inversion on 3-D section based on FEM[J]. Journal of Central South University (Natural Science), 2004, 35(2): 295-299.
[15] ZHANG J, MACKIE R L, MADDEN T R. 3-D resistivity forward modeling and inversion using conjugate gradients[J]. Geophysics, 1995, 60(5): 1313-1325.
[16] 戴前伟, 江沸菠. 基于混沌振荡PSO-BP算法的电阻率层析成像非线性反演[J]. 中国有色金属学报, 2013, 23(10): 2897-2904. DAI Qian-wei, JIANG Fei-bo. Nonlinear inversion for electrical resistivity tomography based on chaotic oscillation PSO-BP algorithm[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(10): 2897-2904.
[17] LI Shu-cai, NIE Li-chao, LIU Bin, SONG Jie, LIU Zheng-yu, SU Mao-xin, XU Lei. 3D electrical resistivity inversion using prior spatial shape constraints[J]. Applied Geophysics, 2013, 10(4): 361-372.
[18] 刘 斌, 李术才, 李树忱, 聂利超, 钟世航, 李利平, 宋 杰, 刘征宇. 基于不等式约束的最小二乘法三维电阻率反演及其算法优化[J]. 地球物理学报, 2012, 55(1): 260-268. LIU Bin, LI Shu-cai, LI Shu-chen, NIE Li-chao, ZHONG Shi-hang, LI Li-ping, SONG Jie, LIU Zheng-yu. 3D electrical resistivity inversion with least-squares method based on inequality constraint and its computation efficiency optimization[J]. Chinese Journal of Geophysics, 2012, 55(1): 260-268.
[19] 吴小平, 徐果明. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 2000, 43(3): 420-427. WU Xiao-ping, XU Guo-ming. Study on 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics, 2000, 43(3): 420-427.
[20] 黄俊革, 阮百尧, 王家林. 坑道直流电阻率法超前探测的快速反演[J]. 地球物理学报, 2007, 50(2): 619-624. HUANG Jun-ge, RUAN Bai-yao, WANG Jia-lin. The fast inversion for advanced detection using DC resistivity in tunnel[J]. Chinese Journal of Geophysics, 2007, 50(2): 619-624.
[21] 朱自强, 曹书锦, 鲁光银. 基于混合正则化的重力场约束反演[J]. 中国有色金属学报, 2014, 24(10): 2601-2608. ZHU Zi-qiang, CAO Shu-jin, LU Guang-yin. 3D gravity inversion with bound constraint based on hyper-parameter regularization[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2601-2608.

