探究中值定理在微分法确定反应级数时的应用

赵爱祥（江苏联合职业技术学院　盐城机电分院，江苏　盐城　224000）

探究中值定理在微分法确定反应级数时的应用

赵爱祥
（江苏联合职业技术学院盐城机电分院，江苏盐城224000）

摘要：本文通过物化实验，将一级反应中的微分法和其他数据模型进行比较，改善了传统实验在数据处理上的问题，简化了数据，减少了实验误差.从而验证了中值定理在微分法确定反应级数时的优势.

关键词：拉格朗日中值定理；微分法；反应级数

微分法的重点在于要根据反应物浓度c随着时间t在某个时间点的变化来求切线斜率.求取这种斜率的方法有很多，如镜面法、等面积法等.镜面法直接自曲线上选取某点进而求斜率，误差较大；等面积法是通过简化计算的方法来获取斜率，误差较小，但是工作量却较大.本文通过中值定理法获取过氧化氢的催化分解数据，同时将这样的数据和其他数据模型进行比较，进而验证了中值定理在微分法确定反应级数时的优势.

1　理论依据

通过中值定理求取曲线上某点导数，实际上是将两实验点中间部分曲线近似为直线.简单级数反应之间的c-t关系可以描述成以下形式：

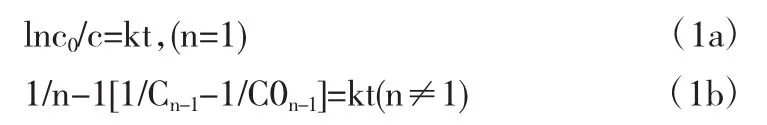
正常情况下，n取值范围在0-3之内，对上面两个式子使用中值定理，无法求出ti+1和ti两点和中值ε关系.因此将上面两个式子展开（按麦克劳林级数）.为确保精确，取前三项为上式近似值，以确保ti+1和ti两点曲线关系：

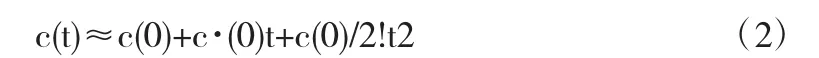
将公式（1a）变形后，有c=c0•e-kt，因此有c（t)=-kc0e-kt；c.（t) =k2c0e-kt，得：

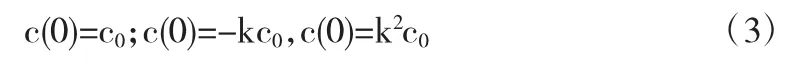
将

（3）式代入（2）有：

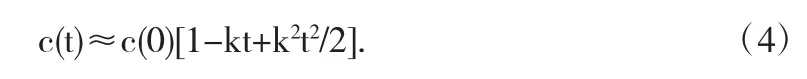
将（1b）转化，如下：

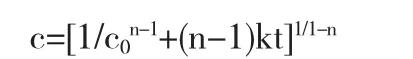
将（5）代入（2）有：

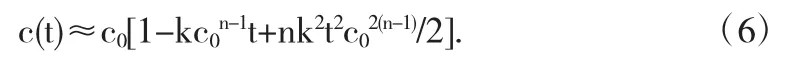
（4）式为反应方程积分近似通式.（6）式为n级反应方程积分近似式子.当n=1时，（4）式和（6）式就变得相同，也就是说（6）是（4）的延伸.将（6）式求导，可知，

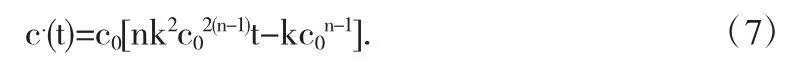
将（6）和（7）式带入中值定理公式，可以得到

也就是说对于简单级数的化学反应，在ti+1和ti时，物质浓度中值导数为

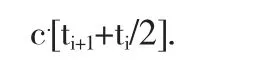
由此可知，导数c.随着ε变化而变化.如果每隔一定时间间隔，对c进行求导，就能够得出c.（ti）随着c（ti）变化的数据，从而确定反应级数.

2　过氧化氢分解下的几类数据模型

探究中值定理在确定反应级数时的应用的过程中，具体以过氧化氢的催化分解为例.将过氧化氢在微分法下的数据模型和其他数据模型进行比较，来验证中值定理在微分法确定反应级数时的优势.过氧化氢催化分解下的各组数据模型如下：

2.1积分法

用KI来催化H2O2分解，在这个过程中，用V∞表示过氧化氢完全分解时产生的氧气体积，Vt表示过氧化氢在t时刻下产生氧气量，k表示速率常数.根据动力学方程中反应物浓度与产物浓度关系，可以得到公式如下：

以ln（V∞-Vt)对t作图，可得一条直线，斜率为k.每一个ln（V∞-Vt)，都会涉及到V∞.测量V∞有以下方法：延长反应时间；加热，冷却到原来温度；增加催化剂KI浓度；引入强氧化剂.这些方法不仅费时费力，而且还容易造成较大误差.

2.2非线性拟合

随着计算机软件的广泛应用，非线性方法处理数据变得越来越容易.最小二乘法就是依据非线性拟合原理改写而成.改写（9），得到如下公式：

通过数学软件就可以得到最优化曲线，因此不必求V∞.

如果实验存在误差，则公式改写成这样：

2.3微分法

微分法使用范围较广，可以应用在任何级数的反应中.通过微分法可以测量反应速率和反应级数关系.对ln（V∞-Vt) =-kt+lnV∞进行微积分，可以得到如下公式：

上面求得的公式为过氧化氢分解条件下的微分方程，以dVt/dt对Vt作图，可得到一条直线，斜率-k.

微分法中，最重要的是求dVt/dt.dVt/dt有多种求法：如等面积法和拉格朗日中值定理法等等.我们这里以中值定理法和等面积法为例，探究微分法中中值定理的具体运算过程.

2.3.1等面积法

将实验所得数据Vt对t进行数据处理，在圆滑曲线上可以得到ΔVt/Δt.在区间t1-t2内，可以得到：

绘制ΔVt/Δt对t的曲线，在图中根据等面积法绘制dVt/dt曲线，与其他方法（中值定理法除外）相比，该方法工作量大，易引起误差.

2.3.2中值定理法

根据中值定理法，有：

当t2-t1很小时，可以近似的认为t=t1+t2/2.

中值定理法应用广泛，能够计算任意时刻的物质反应速率，比其他方法更为准确方便.因此，在用不同方法求反应速率时，中值定理法应用最为广泛.

2.4微积分联合对数

因为Vt与t的变化为非线性，dVt/dt对Vt图像更多集中在横坐标右侧，通过上面的（9）和（14）式子可得：

以ln（dVt/dt）对t作直线，斜率为-k，在ln（dVt/dt）对t直线中，数据分布均匀，图形美观.

2.5速率比法

此种方法建立在拉格朗日中值定理法的基础之上，速率比法需要对dVt/dt进行运算.运算过程中，取t2-t1=Δt，当Δt=1分钟、2分钟、4分钟、6分钟、8分钟、10分钟时，分别求对应数值下的反应速率常数.

根据拉格朗日中值定理公式进行作图.从图像能够看出：当时间在第2分钟、第3分钟时，它们的dVt/dt数值小于第四分钟.相应的ln（dVt/dt）也明显在逐渐减小，有的甚至是负值.速率比法的优势在于通常情况下通过简单作图，就可以得到反应速率常数.

3　中值定理下的过氧化氢分解数据模型

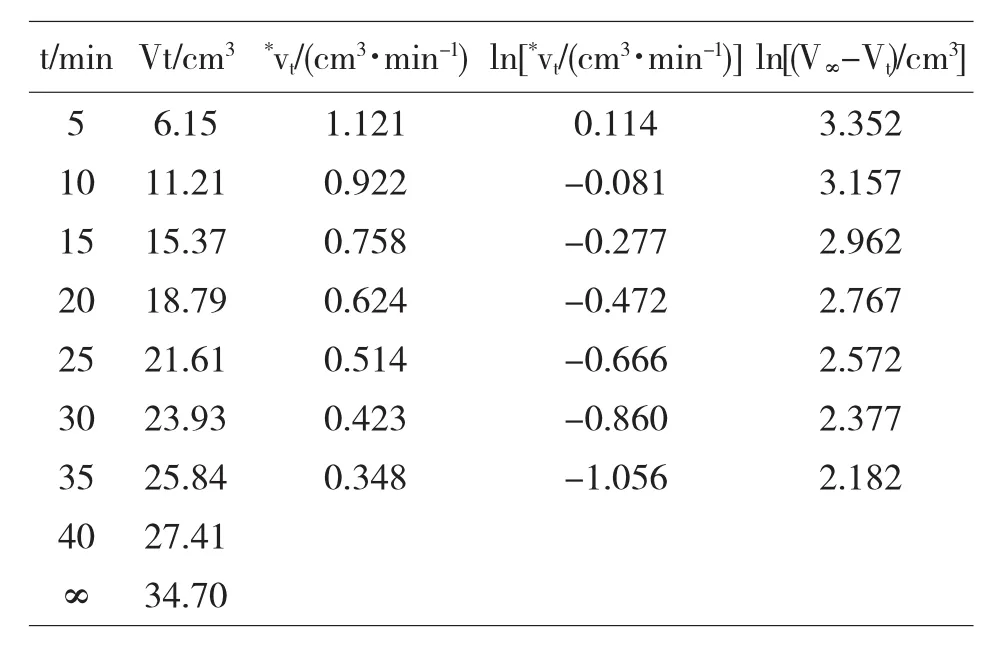
表1过氧化氢的分解数据

通过298k下过氧化氢的分解数据，可以求得其反应级数和速率常数（如表1）.

因为测定结果为生成产物氧气的体积，体积Vt与物质浓度c关系为c=K（Vt-V∞).以ln（dVt/dt)对ln（V∞-Vt)作图可知，图像为一条直线.斜率m=n.在等时间间隔的条件下对中值定理进行求导，将求得导数的一系列数据列成表格，根据表格进行作图（图2）.由图可知，该直线斜率为0.99，由此可以推断该反应为一级反应.用最小二乘法回归，直线斜率和相关系数都无限接近于1.再通过一级反应的ln（V∞-Vt)对t作图，可以得到直线斜率和速率常数，进而求出导数误差.

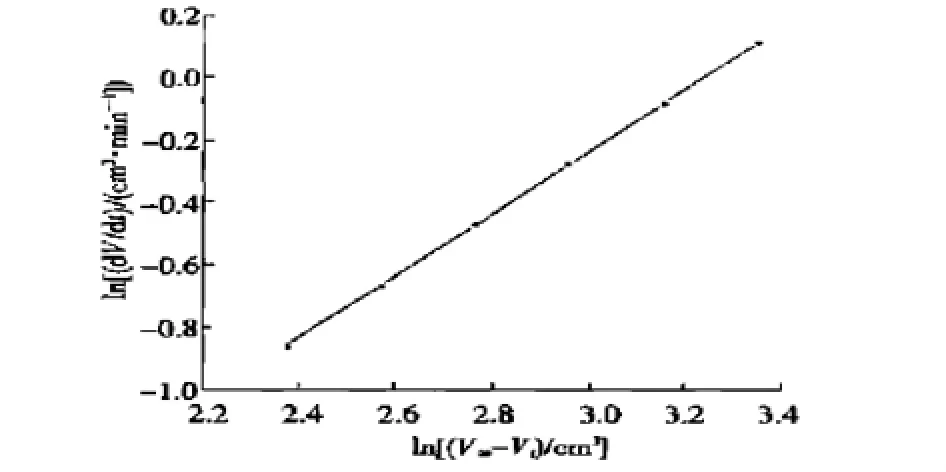
图2微分法求过氧化氢反应级数

4　结果与讨论

通过对简单级数的化学动力学方程进行运算，可以成功得到二次曲线方程.这也证明了使用中值定理可以成功获得曲线上某点切线斜率，从而根据微分法确定反应级数.

中值定理法适用于对时间进行微分的反应.当给定数据是等时间间隔时，经过简单运算就可以得到微分数据，只需要得到lg（c*)对lgc图像就可以确定反应级数，从而突破了以往的限制.

当实验数据不是等时间间隔时，只需要做出c-t图就可以补充缺失数据，进而通过此种实验方法求微分.在（ti，ci）两侧取点，假设有两点（ta，ca），（tb，cb）.则tb-ti=ti-ta条件下，Δt=tb-ta越小，求导误差越小.

微分法不用测量V∞，能避免V∞测定不准造成的误差，它的适用范围非常广泛（确定反应级数，建立速率方程等），可以用镜面法、等面积法、拉格朗日中值定理法等.本文通过拉格朗日中值定理法获取过氧化氢的催化分解数据的研究，证明了中值定理法在微分法确定反应级数时能够得到很好的应用.

参考文献：

〔1〕郭子城，周广芬，中值定理法在微分法确定反应级数时的应用[J].河北科技大学学报，2004(04).

〔2〕刘盛利.中国微积分教科书之研究（1904-1949）[D].内蒙古师范大学，2012.

〔3〕高雪芬.一元微积分概念教学的设计研究[D].华东师范大学，2013.

〔4〕夏爽，唐文广，杨朝晖.Origin与MATLAB在求解化学反应级数中的应用[J].西华大学学报(自然科学版)，2009（04）. 〔5〕刘敏.应用Matlab求取化学反应级数[J].聊城师院学报(自然科学版)，2002（04）.

〔6〕李洪亮，张建立，李鹏.用C++语言从积分法中求反应级数的研究[J].计算机与应用化学，2006（11）.

〔7〕夏爽，唐文广，杨朝晖.Origin与MATLAB在求解化学反应级数中的应用[J].西华大学学报(自然科学版)，2009（04）.

中图分类号：O172

文献标识码：A

文章编号：1673-260X（2015）07-0007-02