基于神经网络模糊PID 的步进电动机控制系统

张琪琪，储春华

(海南大学，海口570228)

0 引 言

步进电动机是一种将脉冲信号转化成相应角位移和直线位移的电动机，每输入一个脉冲，电机就转动固定的角度。其角位移正比于输入脉冲，旋转速度正比于脉冲频率，运行速度和角位移也不受电源电压波动以及负载的影响［1］。因此，通过控制脉冲信号的频率和个数，就可精确控制步进电动机的速度和角位移。由于步进电动机具有高精度定位、快速起停的特点，现已广泛应用于数字控制领域，如软盘驱动系统、数模转换控制系统、绘图仪、打印机、数控机床等。

步进电动机闭环控制常用的方法是PID 控制，但PID 控制适用于具有精确数学模型的线性系统，而步进电动机模型在运行过程中往往是非线性的、时变的，这使得设定的PID 参数控制无法根据变化的条件实时改变控制参数从而得到最优的控制。模糊逻辑控制和神经网络控制都是用来处理非线性、不确定系统的重要控制方法，模糊逻辑控制具有鲁棒性强、容错能力高等优点，神经网络控制具有自我学习、并行处理等优点。本文结合模糊逻辑控制、神经网络控制以及常规PID，利用模糊逻辑规则将状态变量进行模糊化和归一化处理后，再将其作为神经网络的输入，利用神经网络自我适应和学习的特点对加权系数进行调整，根据系统的运行状态自动调整相应参数，最终得到最优的PID 控制参数。该控制器克服了传统PID 控制器参数固定的缺点，可提高系统的控制性能［2-4］。

1 两相混合式步进电动机的数学模型

基于步进电动机的结构及工作原理，A. C.Leenhouts 等根据前人的总结，忽略涡流、磁滞效应、转矩的三次以上谐波以及两相混合步进电动机间的互感现象，提出如下的Leenhouts 模型用以表示步进电动机［5］。

磁链方程:

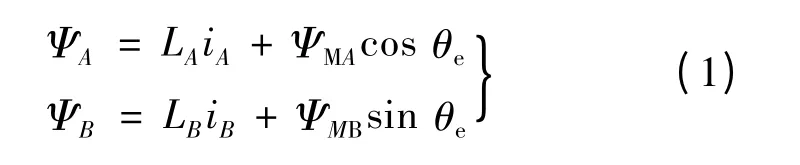
式中:ΨA，ΨB为A，B 相的相绕组的气隙总磁通;LA，LB为A，B 相的相绕组自感;iA，iB为A，B 相的相绕组电流;ΨMA，ΨMB为永磁体在A，B 两相绕组下分别产生的气隙磁通;θe为转子的电角度。

电感方程:

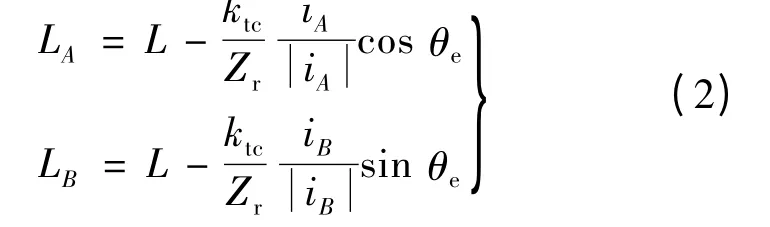
式中:LA，LB为A，B 相的相绕组自感;L 为自感中的恒定分量;iA，iB为A，B 相的相绕组的电流;Zr为转子齿数;ktc为饱和系数;其他为电感的基波分量。

反电动势方程:

式中:uA，uB为A，B 相的相绕组反电动势;kt0为转矩系数;h3为三次谐波转矩系数;θ 为转子的机械角度。且:

基本电路方程:

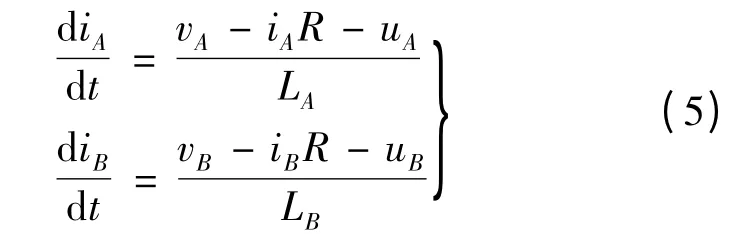
式中:vA，vB是电机A，B 相的总电压;且假设A，B 是相互对称的;R 为两相绕组的总电阻;A，B 相的电磁转矩TA，TB如下:

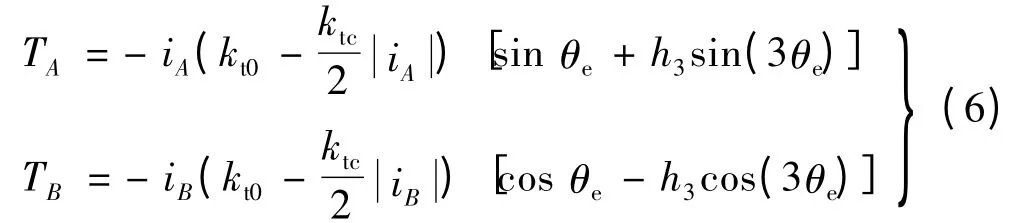
D 为电机的保持转矩幅值，混合式步进电动机的定位转矩:

步进电动机的总电磁转矩:

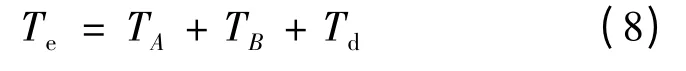
混合式步进电动机的动力方程:

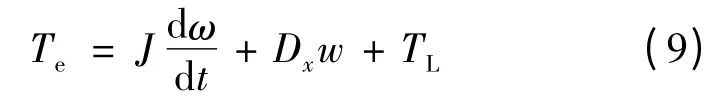
式中:J 为电机的转动惯量;ω 为机械角速度;Dx为粘性摩擦系数;TL为为负载转矩。

上述式(1)～(9)构成了两相步进电动机的数学模型。其相关参数根据常州松洋机电有限公司SY57STH51 -2804B 型步进电动机的相关技术资料和文献确定［6］，自感L =4.34 mH，饱和系数ktc=0.026 4，转矩系数kt0=0.85，转子齿数Zr=50，三次谐波转矩系数h3=0.31，总电阻R=0.83 Ω，电机转动惯量J=275 g·cm2，电机保持转矩幅值D=0.04 N·m，粘性摩擦系数Dx=0.05 N·m·s/rad，绕组电流I=2.8 A。

2 神经网络模糊PID 控制及S 函数实现

在控制过程中最常用的是PID 控制，合理的参数才能使控制系统得到良好的性能。传统的PID 控制器参数需要人工反复试验确定，本文利用神经网络自我学习的特点，结合模糊逻辑控制根据系统的运行情况，使输出层神经元的输出状态与PID 控制器的参数Kp，KI，KD相对应，通过神经网络的自我学习以及模糊逻辑的处理，实现加权系数的调整以及模糊逻辑的处理，从而达到性能指标最优化的PID参数［7］。基于神经网络的模糊PID 控制器由三部分组成:(1)传统的PID 控制器;(2)模糊化模块;(3)神经网络。

传统的PID 控制器利用PID 控制与步进电动机进行闭环控制，且其增量式PID 控制可以表示:

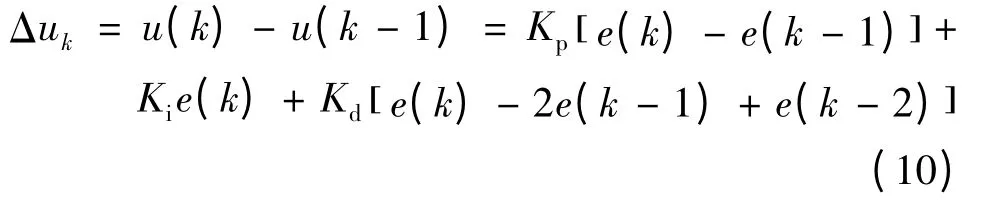
式中:Kp，KI，Kd分别对应比例、积分、微分系数，Δuk为控制量的增量;e(k)为误差。

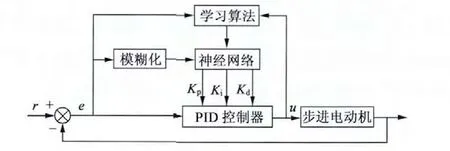
图1 神经网络模糊PID 控制系统结构图

模糊化模块利用模糊控制理论对神经网络的输入进行预处理，具有鲁棒性强和非线性控制等优点，可以避免神经网络因输入量过大而导致的神经元对输入敏感性下降的缺点。此模块将 e(k{ })进行模糊量化和归一化处理。通过计算e(k)/r(k)，将系统的误差e(k)归一化，并在闭区间［0，1］内完成模糊量化，并将误差传给神经网络。

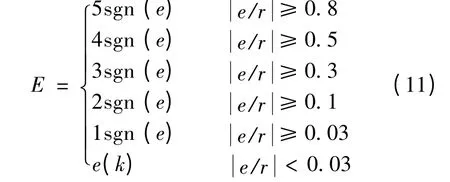
式中:E 为系统误差的模糊论域。

神经网络模块将模糊处理后的误差作为输入，利用神经网络的自我学习对加权系数初值进行调整，再由系统的运行状态调整PID 控制器的参数Kp，Ki，Kd。此模块结构如图2 所示，有M 个输入节点、Q 个隐含节点、3 个输出节点。输出节点对应着PID 的三个参数，而控制器的参数Kp，Ki，Kd不能为负，因此取非负的Sigmoid 函数作为输出层神经元活化函数，取正负对称的Sigmoid 函数作为隐含层神经元活化函数。

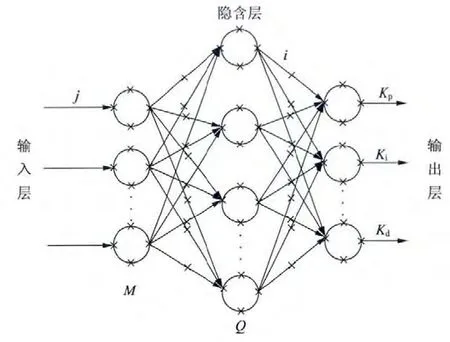
图2 BP 神经网络结构图

神经网络输入:

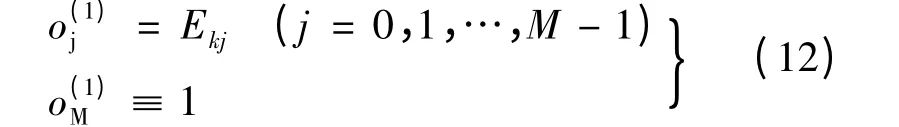
隐含层的输入输出为:

式中:oj为输出值;neti为净输入值;wij为权系数;sigmoid 活化函数f［x］=tanh (x)角标，(1)、(2)、(3)分别为神经网络输入层、隐含层、输出层。

输出层的输入输出:

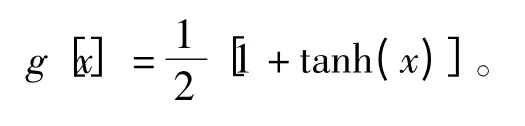
神经网络输出层加权系数:

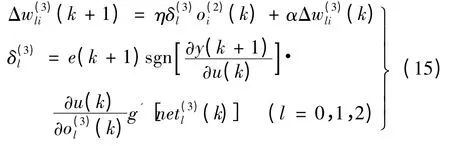
式中:η 为学习速率;δ 为惯性系数。

隐含层加权系数:

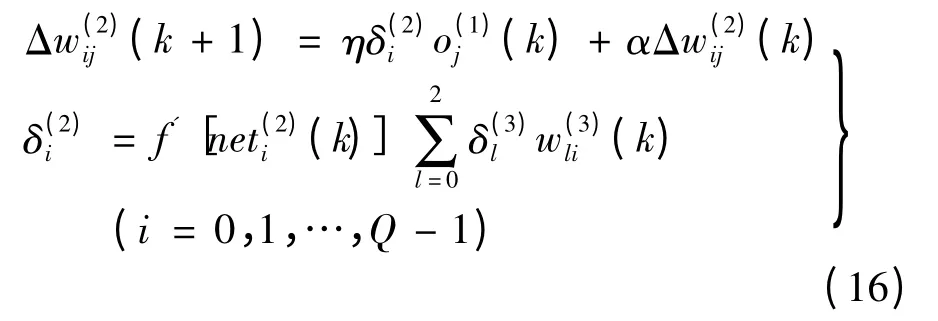
本模型选取4 -5 -3 结构的神经网络，学习速率取0.25，惯性系数取0.05。由于Simulink 没有与此算法相关的PID 控制器，此处通过编写S 函数并将其装封在神经网络模糊PID 模块中实现对步进电动机的控制［8］。图3 为PID 参数在线自整定的过程，由于篇幅所限，S 函数程序略。

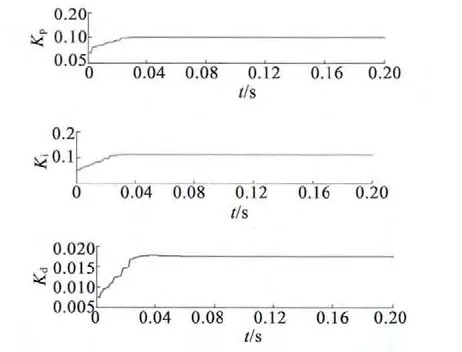
图3 神经网路模糊PID 参数自整定

3 模型设计与仿真分析

3.1 模型设计

利用MATLAB 中的Simulink 工具箱，结合式(1)～式(9)的步进电动机数学模型，建立两相混合式步进电动机的仿真模型。步进电动机的仿真模型如图4 所示，由电压、电流、电感以及机械四个模块组成。其中，TL为输入负载转矩，A +，A -，B +，B-为A，B 两相的输入电压，m 则为整个电机模型的输出，该输出信号包括了输出电压、电流、转矩、角速度以及转子位置信号。

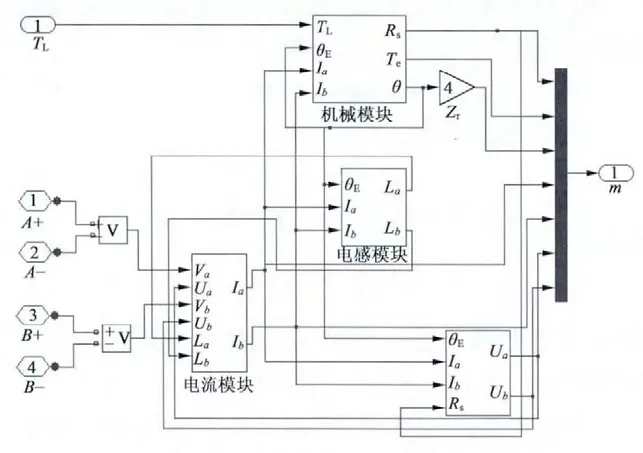
图4 步进电动机的仿真模型

模型中对步进电动机的驱动采用环形分配器、PWM 发生器和H 桥的驱动电路。环形分配器模块由环形计数器和逻辑电路组成，PWM 发生器模块采用电流滞环控制型，将环形分配器产生的一定相序的脉冲信号转换成PWM 电流信号，再与反馈电流信号进行滞环控制，从而产生驱动H 桥MOSFET 管的驱动信号，H 桥模块则采用传统拓扑结构的双H 桥驱动步进电动机的A，B 两相电流［9］，如图5 所示。

神经网络模糊PID 控制的步进电动机整体仿真模型如图6 所示。

图5 仿真模型及两相电流

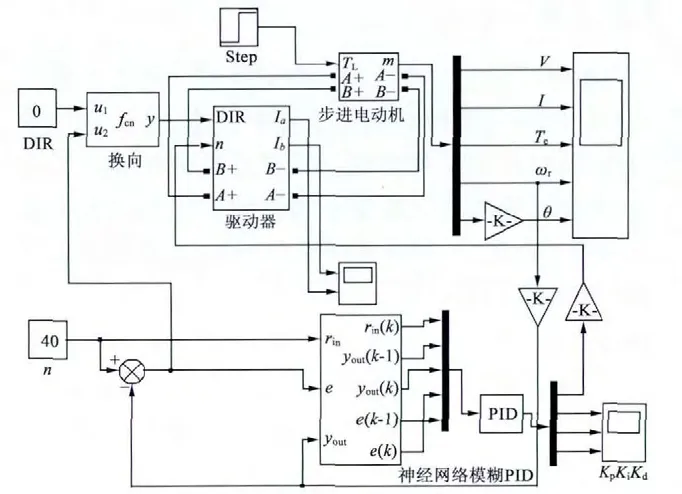
图6 两相混合式步进电动机神经网络PID 控制系统仿真模型

3.2 仿真分析

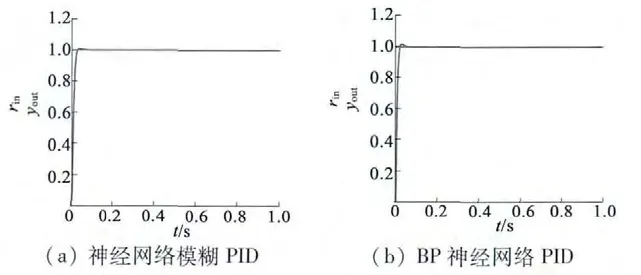
图7 阶跃响应

3.2.2 系统运行仿真分析

空载起动时，设定初始转速为40 r/min，起动时转矩、转速如图8 所示。步进电动机在起动时，转速有较大的波动，但在很短的时间内趋于稳定，最终在给定值附近一定范围内波动。转矩在起动时波动较大，在速度达到给定值时稳定在0 附近波动。

图8 步进电动机空载起动仿真

空载起动，给定转速40 r/min，并在0.05 s 时突增0.4 N·m 的负载转矩，转速、转矩如图9 所示。从图9 中可以看出，在0.05 s 时负载转矩突然增大到0.4 N·m，使电磁转矩瞬间增大，此时转速随之出现较大的波动，很快转矩稳定在0.4 N·m 左右，在转矩稳定时转速也稳定在给定的40 r/min 上下波动。

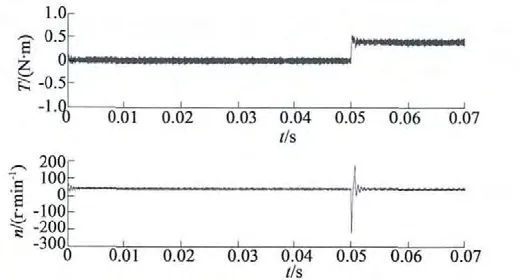
图9 神经网络模糊PID 空载步进电动机突然加负载转矩仿真

分析仿真结果得出，步进电动机控制系统在空载起动和起动后负载突然增加时，系统响应快，暂态过程时间短，转矩和转速的波动小，故神经网络模糊PID 控制系统对步进电动机控制性能有一定的提高。

4 结 语

本文在步进电动机的运行原理和前人总结的数学模型的基础上，搭建了两相混合式步进电动机模型，环形计数器和逻辑电路组成的环形分配器、滞环控制的PWM 发生器和传统H 桥结构组成驱动电路模型，并对神经网络模糊PID 控制算法进行简析，构建了神经网络模糊PID 控制的步进电动机闭环控制系统。从仿真结果看，该系统与单纯的神经网路PID 控制系统相比，具有响应速度快、超调小、抗负载冲击能力等良好的静、动态特性。该仿真系统对步进电动机控制系统的设计以及控制算法的改进提供了一定的参考，具有良好的推广和应用价值。

［1］ 冯秀清，邓星钟等.机电传动控制［M］.5 版.武汉:华中科技大学出版社，2011:92.

［2］ CHANG W - D，HWANG R - C，HEISH J - G. A multivariable on1ine adaptive PID controller using auto-tuning neurons［J］.Engineering Applications of Artificial Intelligence，2003，16(1):57 -63.

［3］ HUANG S N，TAN K K，LEE T H.A combined PID/adaptive controller for a class of nonlinear system［J］. Automatica，2001，37(5):611 -618.

［4］ 陶永华，尹怡欣，葛芦生. 新型PID 控制及其应用［M］. 北京:机械工业出版社，1998:136 -176.

［5］ LEEHOUNTS A C.Step motor system design handbook［M］.USA:Litchfield Engineering Co.，1991:4 -7，35 -36.

［6］ 邹乾.两相混合式步进电机的模糊PI 控制方法研究［D］. 杭州:浙江大学，2010.

［7］ 刘霜.混合式步进电机的神经网络控制方法研究［D］. 杭州:浙江大学，2013.

［8］ 刘金琨.先进PID 控制MATLAB 仿真［M］.3 版.北京:电子工业出版社，2011.

［9］ 周一飞.基于Simulink 的步进电机控制系统仿真［D］.成都:西南交通大学，2014.