多目标规划模型在城市零担配装成本优化管理中的应用
钟 苹,龙桂先
(1.南宁职业技术学院,广西 南宁 530008;2.广西财经学院,广西 南宁 530003)
多目标规划模型在城市零担配装成本优化管理中的应用
钟苹1,龙桂先2
(1.南宁职业技术学院,广西南宁530008;2.广西财经学院,广西南宁530003)
南宁职业技术学院2014年度科研立项项目“南宁专线物流联盟标准化体系研究”(编号:2014YB12)
摘要:文章以车辆标记最大载重、最大载货容积限制以及货物不可分装作为约束条件,建立研究“城市货的”货运中转配载的多目标规划模型,并以广西宅配通有限公司为例进行了模型应用分析。结果表明,该方法简单可行,给公路零担货运企业提供了理论参考,对于解决现实问题中的中转装车问题具有重要的价值和现实意义。
关键词:运输经济;成本优化;多目标规划;零担货运;配装优先级
0引言
“城市货的”是城市运营日常生活工作中物流配送小型搬运的一种货物运输车辆、或货运出租车的简称。在公路运输中,居于城市区域范围内的城市货的——“宅配通”这一新兴业务在传统的公路零担货运上,管理和服务有所创新,但是在资源的消耗量上依旧居高不下,如何快速高效的对各种货物进行配装,降低资源的使用量,就成了城市货的当前亟待解决的一个问题。
本文以广西城市货的样板——广西宅配通有限公司为例,提出采用多目标规划模型的方法对当地城市货的货运运营进行分析,为当地城市配送业务降低运输配送成本提出优化方案。
1广西宅配通零担货运现状问题及分析
1.1 货源组织力度不足
广西宅配通有限公司的配送范围主要是以高新区科园大道的规划总部为出发点的内环以内的青秀区、西乡塘区、兴宁区和江南区,配送范围有限,揽货量也相对有限,每天出库的快件量大概为3 000件,每月的出库量约有10万件。由于区域覆盖面低,导致花费大部分的时间在货物的组织过程中,货车运营效率低,运输组织程度低。
1.2 配载的计划性差,配送效率低
宅配通零担货物运输信息不畅,从揽货到高新区总部入库货品信息以手工录入为主,所有待配送货物在进入仓库后,不能及时根据货物的信息对货物进行编排和预处理,因此在车辆的选择和货物的配装上,难以达到预期的目标,车辆的容积利用率<70%。
在出库时,仅仅满足“先进先出,后进后出”,在车辆的选择以及货物的配载上,无法立刻做出响应,完成积载计划,再加上宅配通没有采用货物追踪系统以及先进的通讯技术装备,无法实现“货物交接清楚之后能在3 h之内将货物安全送达客户手上”的要求。
此外,宅配通的两种车型都是中小型的普通货车,针对特殊货物时只能另外选择车辆或者租赁车辆,配送效率低且成本高。
1.3 经营业务单一
宅配通目前只停留在为商家和企业提供城市货配送的阶段,且对象非常固定,还不具备为客户提供全面的物流网络设计的能力,一旦这些商家或者企业寻找到更加优质的合作对象,而企业一时又难以满足大众客户的货物配送需求,企业将面临前所未有的运营困境。
2多目标规划模型的建立
考虑到企业的实际情况,单一目标规划模型不能够针对性地解决以上三个问题,因此本文考虑建立多目标规划模型,设置目标函数:(1)配载货物的优先级最大化。优先配载加急货物,在限时内送达客户。(2)车辆有效载重利用率和总体积利用率最大化。对货物进行预处理,充分利用车辆的运载空间,在尽可能提高每一配送车辆满载率的基础上降低车辆的平均使用频率,减少车辆的油耗和车辆的损耗,降低企业的物流运输成本。(3)相对于运达期限的运送富裕时间的数学期望值最小。通过已知的运到期限和已在途时间,计算出货物的运送富余时间,按照富余时间,在配载时对货物进行调整,做到货物在交接清楚之后的3 h之内将能够安全地送至客户手上,减少客户投诉,体现客户需求至上。
通过主要目标法,将函数的主要目标,实现车辆的满载率作为唯一目标,将次要目标转化为约束条件,实现多目标规划模型向单目标规划模型的转变,从而简化计算,提高计算效率,并通过随机解的产生规则得到单目标规划问题的有效解,即可作为多目标规划模型的最优解。具体解法如下:
2.1 参数定义
定义如下符号:n为待配装货物的总数量,中转站待配送货物集i={1,2,…,n},其对应的各批货物的重量和体积分别为Wn={w1,w2,…wn}和Vn={v1,v2,…vn},m为零担货物作业车的总数量,车辆j(j=1,2,…m)剩余载重量和载货容积分别为Wm={w1,w2,…wm}和Vm={v1,v2,…vm},Wj表示车辆标记的最大载重量,Vj表示车辆最大载货容积,Ti为货物已知在途时间(包涵前程运输时间和落地入库保管时间),Tei为中转装车之后的后程运输时间(以零担货物出库配装的时间点为计算节点)。
定义xij为0-1决策变量,且
定义α为货物装载情况的判断决策变量,且
αi=∑mj=1xij,即ai的实际含义为
2.2 目标函数
第一个目标函数:受车辆类型的限制,配装问题所要考虑的两个必要因素是使得车辆装载货物的总重量和总体积达到最大,分别表示为:
maxZw=∑mj=1∑ni=1wixij
(1)
maxZv=∑mj=1∑ni=1vixij
(2)
在没有特别要求重量或体积目标时,可用“载货的平均容重尽量接近车辆的容重”来替代(1)和(2)两个目标,即:
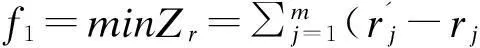
(3)
式中:r′j——j辆车载货的平均容重;
rj——表示第j辆车的容重。
第二个目标函数:在满足货物的数量最大化要求的基础上,确保重点物资,急需物资及核心货物优先配装。因此,待装货物赋予优先级pi=(pi≥0,i=1,2,…,n),其中,pi值越大,则装车顺序越靠前,pi值越小,则装车顺序越靠后,那么,配装货物的优先级最大化可以表示为:
f2=maxZp=∑ni=1pixij
(4)
第3个目标函数:相对于运达期限的运送剩余时间(Di-Ti-Tei)要最小。即:
(5)
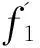
(6)
2.3 约束条件
约束条件是指在公路零担货运场站车辆配装过程中已知的并必须遵守的前提条件。在这里,货运中转装车配送问题的约束条件有3个:
约束条件1:货车核定载重限制,即任何一辆车中转配载的货物的重量不得超过车辆出厂规定的标定值。
∑ni=1wi·xij≤Wj,j=1,2,…,m
(7)
约束条件2:货车载货容积限制,即配载的货物总体积不得超过托运车辆的最大载货容积。
∑ni=1vixij≤Vj,j=1,2,…,m
(8)
在实际中转装车配送问题中,上述两个约束条件所对应的解空间RC是宽松的,会产生许多满足条件的劣质解,因此,为了过滤掉劣质解,加入以下两个约束条件。
(1)载重量使用约束。任意一辆车配载货物达到一定数量时,其剩余载重量都无法再装载任意一批尚未被配装的货物,即:
∀αi=0均有wi>Wj-∑ni=1wixij
(9)
(2)车辆容积使用约束。任意一辆车配载货物达到一定数量时,其剩余载货空间都无法再装载任意一批尚未被配装的货物,即:
∀αi=0均有vi>Vj-∑ni=1vixij
(10)
因为载重量使用约束和车辆容积使用约束不能割裂开来单独考虑,因此,将2个约束条件合并为一个,称为满载约束。即
∀αi=0均有wi>Wj-∑ni=1wixijor vi>Vj-∑ni=1vixij
(11)
约束条件3:一批货物不可分装的限制。即每批货物最多只能装入一辆车内。
∑mj=1xij≤1,i=1,2,…,n
(12)
2.4 多目标规划模型
建立公路零担货运中转装车问题的多目标规划模型如下:
min(f1,f2,f3)ω,使得
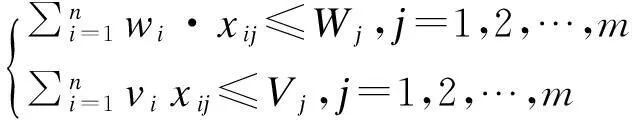
∀αi=0均有
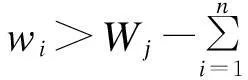
或者
vi>Vj-∑ni=1xijvi
(14)
若记f=(f1,f2,f3)C,RC为解空间,那么模型可以简记为
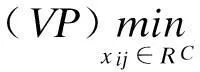
(15)
(VP)表示该问题为多目标规划问题,能够满足目标向量f=(f1,f2,f3)C的解称为多目标问题的绝对最优解。但是由于目标向量的不对称性和约束函数的存在,所以绝对最优解一般不存在于解空间RC。多目标规划问题(VP)一般只能得出有效解或者是弱有效解,用来替代最优解。因此,在这里将多目标规划问题转化为单目标问题进行求解,采用主要目标法,将第一目标函数确定为首要目标,将第二、第三目标作为次要目标,同时,为每个次要目标确定一个适宜的范围值后,将其转化为约束条件。此时多目标规划问题转化为单目标规划问题,通过解决单目标规划问题,找到最优解,作为原来多目标问题的有效解或弱有效解。
首先考虑到车辆的标记载重量和载货容积最大化,并能够确保货物配装的优先级得到满足,同时确保相对于运达期限的运送富裕时间的数学期望值不高于一个给定的数值,进行单目标规划模型及其转化。以多目标规划问题(VP)中的f1为主要目标,根据f2,f3的最低界限即理想点,给定f2,f3的适宜界限值β1,β2,并将其转变为两个约束条件。这样多目标规划问题(VP)就转化为如下的单目标规划问题(SP),即
(SPT)maxU=f1,使得
(16)
∀αi=0均有
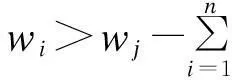
或者
vi>Vj-∑ni=1xijvi
(17)
为了减少货物预处理的复杂程度,在这里,主要以能否和其他货物混装作为对货物预处理的主要依据。首先,将有混载限制的货物从所有等待装车配送的货物分离出来,再将剩下的,可以与其他货物无条件配装的普通货物划分为q1,q2…,qn等若干个配装集(如图1所示)。
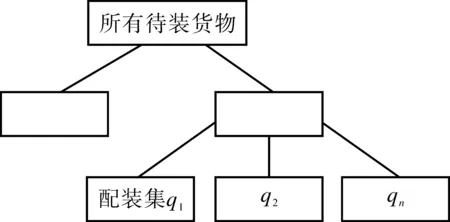
图1 货物的预处理示意图
单目标规划问题加入了f2≥β1、f3≤β2两个新的约束条件,解空间变为多目标规划解空间的子集,单目标规划问题求得的解实际上比多目标规划问题求得的解的数量和范围缩小了。
2.5 解的编码
为了提高计算的效率,将解的矩阵即0-1稀疏矩阵压缩为一个向量,向量的元素序列对应货物的序列,这样,向量元素的取值就不再是0-1,而是采用0-k的取值,即:
Vn={α1,α2,…αn}
(18)
其中,
单目标规划问题的适应函数与目标函数的表达方式一致,因为其目标函数也为取得最大值。所以,单目标规划问题的适应函数又可以表示为f=U=f1。
2.6 随机解的产生规则
随机解产生的过程:首先货物的配载装车是一个随机的过程,即从不受混装限制的货物集或者受混装限制的货物集Q中随机选取1批货物,随机装载到m辆车中的任意1辆,并保证满足约束条件不超过车辆剩余的载重量和载货容积。当配载车辆的剩余载重量和剩余载货容积接近边缘状态时随机装载暂时结束。对所有未装载货物进行统计,如果未被配载的货物其重量或体积相对于已经装车的货物,更能够满足或者接近满载的条件约束,则对产生的随机解进行取舍,如果随机解满足f1≥β1且f2≤β2,那么接受该方案,若随机解的f1<β1或者f2>β2时,那么不接受该方案,此时,该问题解空间为无效解,终止计算,调节β1和β2取值大小之后再进行求解过程。
2.7 计算结果与分析
以广西宅配通有限公司为例,对相同去向的一批货物进行预处理,按照货物的性质,以及混装与不可混装等要求,分成53批货物,经预处理的货物信息如表1所示,分别装入2辆标记的载重辆为3.5t、2t,载货容积为8m3和4m3,剩余载重量为1 200kg、500kg,载货容积为1.8m3和0.8m3小货车中。
为了便于计算,在求解单目标规划问题的过程中,随即抽取的货物的运送富余时间,其数值都大于或等于β2,这样,无论如何随机组合装车的货物批次,均能满足运送平均富余时间大于或等于给定的β1的取值,满足由目标函数三转化而成的约束条件。同样,配装优先级也采用上述方式。
单目标规划模型中的β1和β2的首次取值分别设置为1 500和3,则计算得到的多目标规划问题的有效解或单目标规划问题的最优解的编码为:
S0=(1,1,1,1,1,1,1,0,1,0,1,1,1,1,1,1,0,0,1,1,0,1,1,1,1,1,1,1,2,2,2,1,1,2,1,2,2,1,2,2,1,1,2,1,1,1,2,2,2,1,1,2,1)
此时f1=1 872>β1=1 500,f2≈3.34>β2=3,不符合随机解满足f1≥β1且f2≤β2的条件,为无效解,所以不接受该方案,调整β2的取值为3.5,继续求解。
此时β1=1 500,β2=3.5,计算得到的多目标规划问题的有效解或单目标规划问题的最优解的编码为:
S0=(1,1,1,1,1,0,1,0,1,0,0,1,1,1,0,0,0,0,1,1,0,1,1,1,1,1,2,2,1,2,1,1,1,2,1,1,2,2,1,1,1,1,1,2,1,1,1,1,1,1,1,1,1)
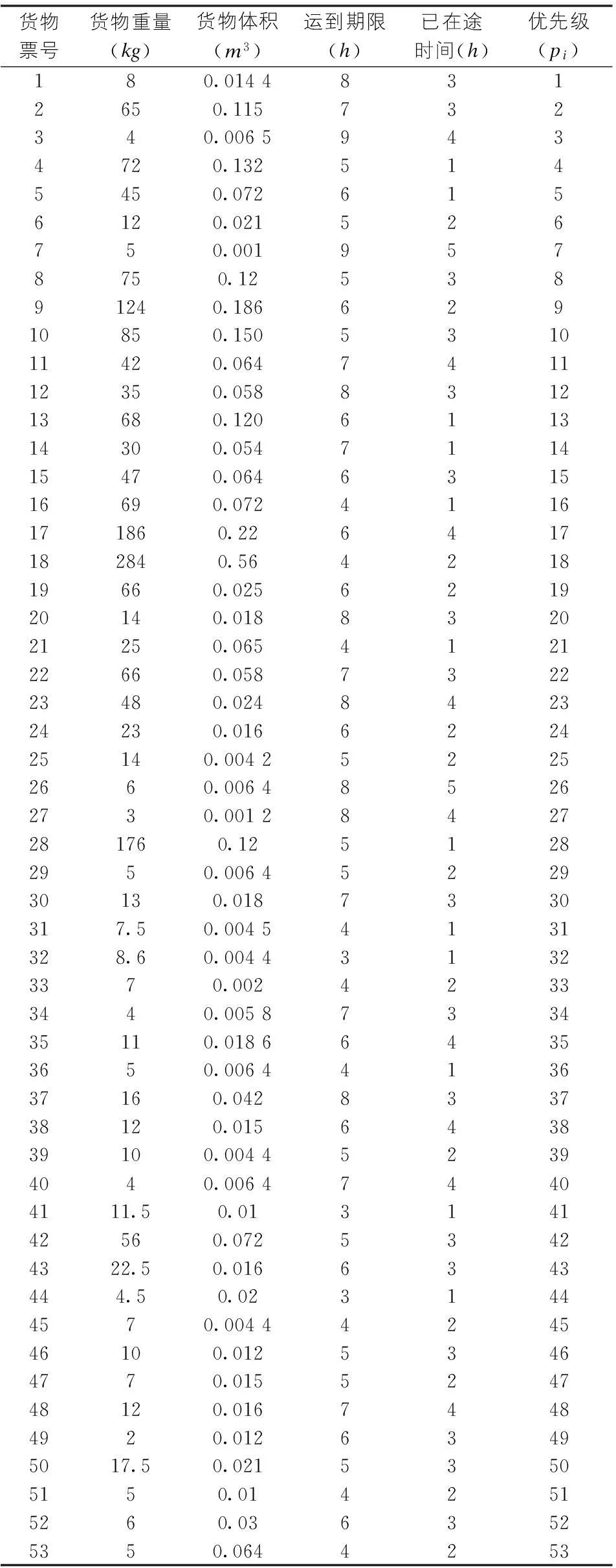
表1 货物数据表
此时f1=1 547>β1=1 500,f2≈3.41>β2=3.5,满足f1≥β1且f2≤β2的条件,为有效解,接受该方案,则:
目标函数值f=f1=0.623
对应的单目标规划模型中,f2=1 547,f3=3.41。
该结果表示配装方案中,等待装货的车辆的剩余容重利用率为0.623,货物装车的优先级为1 547,所有待装货物的平均后程运送时间为3.412 h。装载货物与车辆的使用情况如表2所示。
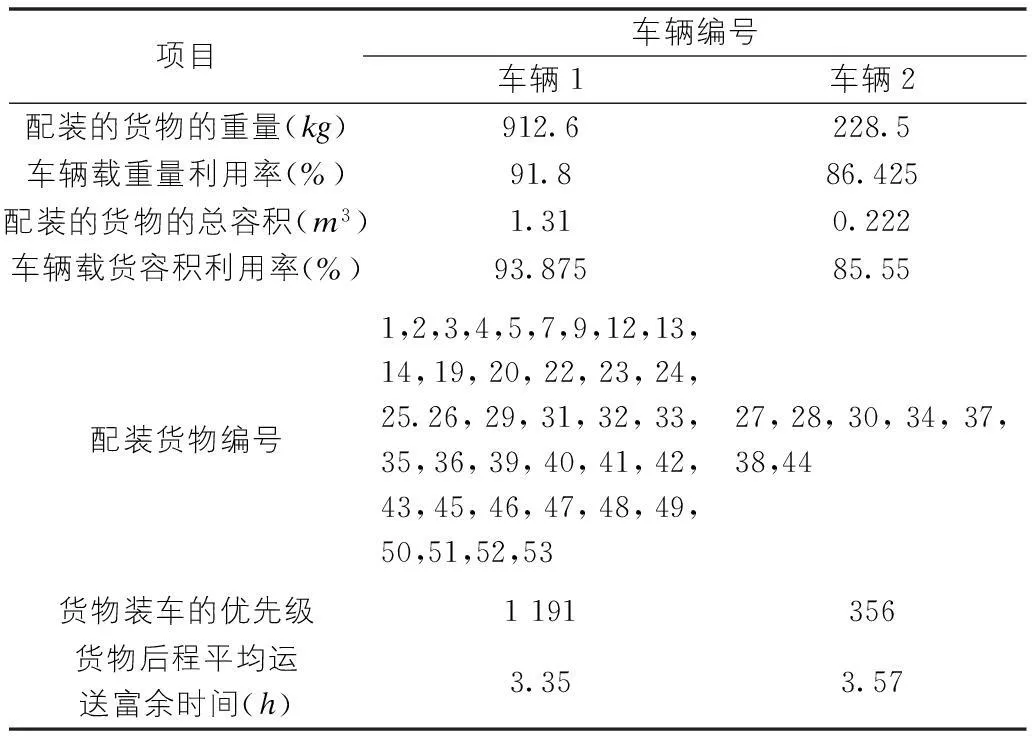
表2 货物装载以及车辆使用具体情况表
从表2的配送方案可以看出,车辆的平均空间利用率超过90%,而之前宅配通配送车辆的空间利用率一般在80%~85%之间。即使取最高值85%作为平均利用率,也就意味着原来车辆出勤18次配送的货物量,现在只需17次就能完成,大大提高了车辆的利用率,减少了企业的物流成本,而且配载过程中充分考虑了货物的优先级以及后程的送达时间,有利于保证货物在时限内送到客户手中,提高客户的满意度。
不足的是,简化的计算方案虽然能求解出多种装车方案,但是装车过程中由于在货物批次的随机组合上限定了范围,因此,求得的只能是多目标规划问题的有效解,而不是最优解。但是,也可以看出,表2的配载方案并不是最优方案,在车辆的利用上,企业还有很大的改进余地,在节省企业成本以及为客户提供优质的服务的问题上,还能够更高效。
3结语
本文将车辆载重标记、载货容积标记以及一批货物不可分装作为约束条件,建立了公路零担货物中转配装的多目标模型,并对模型进行了求解。计算结果表明:配装方案在满足车辆载重与载货容积约束的基础上,最大化满足了车辆的满载率,提高了企业车辆的运输效率,降低了企业的物流成本。本文的方法简单可行,给公路零担货运企业提供了理论参考,对于解决现实问题中的中转装车问题具有重要的价值和现实意义。
参考文献
[1]姜桂宝,刘文峰.公路货运配载问题的研究[J].甘肃科技,2005,21(11):158-160.
[2]赵峰.物流中心货物配装问题研究(硕士学位论文)[D].长春:吉林大学,2005.
[3]马艳玲.物流中心货运配载系统优化研究:(硕士学位论文)[D].上海:上海海事大学,2006.
[4]徐大亮,刘小群.多品种货物配装的优化方法[J].华中科技大学学报(自然科学版),2003,31(9):15-17.
[5]李致中.零担货物配装的数学模型[J].系统工程,1987,5(2):34-39.
[6]曹明兰.配送中心货物优化配装问题的模型与算法研究:(硕士学位论文)[D].北京:北京交通大学,2007.
[7]史亚贝,杨笋,杨荷.零担货物配装问题的算法和系统设计[J].组合机床与自动化加工技术,2008(3):86-88,95.
[8]张春梅,菅美英.用改进的遗传算法求解危险货物零担运输多目标配装问题[J].数学的实践与认识,2010,5(9):121-127.
Application of Multi-objective Programming Model in Urban LTL Loading Cost Optimization Management
ZHONG Ping1,LONG Gui-xian2
(1,Nanning College for Vocational Technology,Nanning,Guangxi,530008;2.Guangxi University of Fi-nance and Economics,Nanning,Guangxi,530003)
Abstract:With the vehicle’s marked maximum load and maximum cargo volume as well as its unsplitta-ble cargo loading as constraints,this article established the multi-objective programming model to study the cargo loading and stowage during “urban goods”transit,and conducted the model application anal-ysis with Guangxi City Express Services Co.,Ltd.,as the example.The results showed that this method is simple and feasible,providing the theoretical reference for highway LTL freight enterprises,with the important value and practical significance for solving the transit loading problem in the practices.
Keywords:Transport economy;Cost optimization;Multi-objective programming;LTL freight;Loading priority
文章编号:1673-4874(2015)12-0068-06
中图分类号:U492
文献标识码:A
DOI:10.13282/j.cnki.wccst.2015.12.016
基金项目
作者简介
钟苹(1977—),副教授,研究方向:物流管理;
龙桂先(1975—),讲师,硕士,研究方向:物流管理。
收稿日期:2015-11-05

