金属镜面双反射消偏研究

鲜于子安 侯立周

（北京空间机电研究所，北京 100094）

0 引言

保持光辐射偏振状态的稳定，对于很多以光为载体的空间光学遥感系统、空间光通信系统等都有重要的意义。例如，在偏振遥感探测中，经过光学系统后到达探测器件的光辐射偏振状态必须与进入光学系统之前的光辐射偏振状态一致，否则会得到物体错误的偏振信息；在相干光通信中，接收端输入信号的偏振状态必须与本振信号偏振状态相匹配，否则将会引入偏振噪声；在空间量子秘钥通信系统中，偏振状态变化引入的量子误码会直接影响秘钥分发系统的安全性[1]。由于反射镜经常被用于光学遥感或光通信等系统，根据偏振光学原理，反射镜一般会改变光子反射前后的偏振状态。为了弥补这种偏振状态的变化，通常的做法是在反射镜上镀多层偏振补偿的膜系结构[2]。但对于需要在星上运行的膜系结构而言，很有可能遇到以下三个困难：1）复杂的膜系结构必须能够承受航天器发射和运行过程中的应力变化；2）膜系结构应当能够在长时间的空间辐照下保持性能稳定；3）在精跟踪状态下反射镜需要随时改变反射角，因此膜系结构必须在反射角变化时依然保持稳定的偏振无关特性。

从提高系统稳定性、延长运行时间以及降低系统复杂度等角度来看，需要特别为偏振敏感的星载光学系统设计一套偏振补偿的反射结构。在偏振遥感探测的实践应用中，美国的地球观测扫描偏光计（earth observing scanning polarimeter，EOSP）[3]、研究型扫描偏光计（research scanning polarimeter，RSP）[4]、气溶胶偏振探测器（aerosol polarimetry sensor，APS）都采用了正交金属反射镜作为光辐射信息的收集装置[5]，这是金属反射镜双反射消除偏振的一种特例。此外，由于实际中各种影响因素的存在[6]，完全消除偏振十分困难。本文选取了五种常用于反射镜镜面镀膜的金属材料，对金属反射镜双反射消除偏振的过程和若干影响因素中的主要因素进行了分析和仿真，给出了仿真结果。

1 金属镜面双反射消偏原理

1.1 金属表面的反射过程

由于金属电导率不为零，因此金属是有损耗电介质，其折射率为复数。当光线照射金属表面时，其反射过程仍遵循折射定律和反射定律[7]。金属表面反射如图1所示。

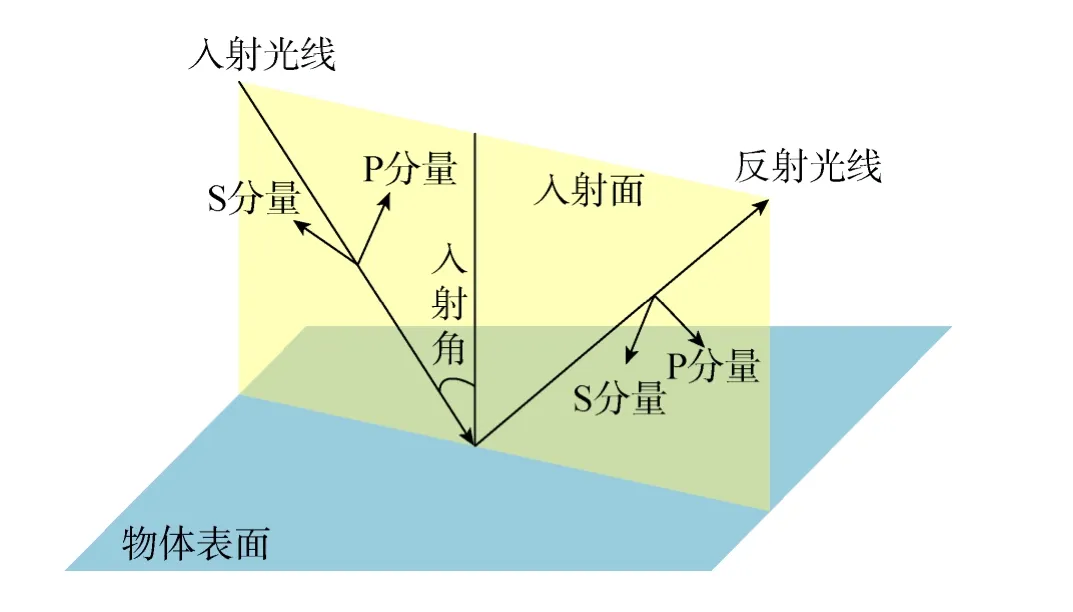
图1 物体表面的反射Fig.1 Reflection on the surface

设n1、θi为入射介质的折射率和入射角；= n2- in2k为金属材料的复折射率，其中n2为金属的主折射率，i为虚数单位，n2k为金属的主损耗率[8]，于是k为金属主损耗率与金属主折射率的比值。

定义中间变量a、b：

定义垂直于入射面的S分量的反射系数为sr，平行于入射面的P分量的反射系数为rp，垂直于入射面的S分量的相位变化为sφ，平行于入射面的P分量的相位变化为pφ[9]，据菲涅尔折反射定律[10]，可表示为：

通常S分量和P分量的反射率和位相变化通常不同，从而导致了金属表面的反射光与入射光的偏振状态不同，这种不同是由反射镜自身引起的，称之为“额外偏振”。

1.2 双反射的Stokes矢量和Mueller矩阵表达

利用两片反射镜使光线经过双反射，并且双反射的入射面相互垂直，在这个条件下，如果再让双反射过程的入射角相同、镜面特性相同，则理论上可以不引入额外偏振。原因是：第二次反射引起的额外偏振“抵消（或补偿）”了第一次反射引起的额外偏振，从而达到了双反射消除偏振的目的。双反射过程如图2所示。

图2 双反射消除偏振Fig.2 Elimination polarization of double reflection

光的偏振状态和传播特性可以用 Stokes矢量和 Mueller矩阵描述[10]，Stokes矢量的表达式为，其中s为总光强，s为0°与90°线偏振光的强度之差，s为45°与135°线偏振光012的强度之差，而s3为左旋与右旋圆偏振光的强度之差。

图2中反射镜1上入射光和反射光的Stokes矢量分别为 S0、S1，反射镜2上入射光和反射光的Stokes矢量分别为 S2、 S3，于是整个过程的输入光和输出光分别为 S0、 S3。

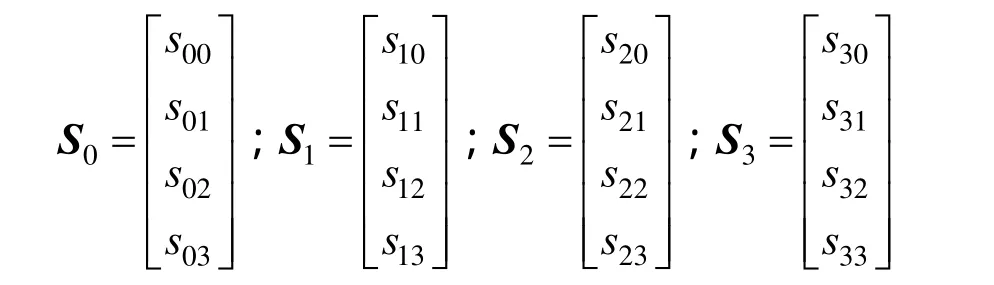
双反射过程中，反射镜1、2的Mueller矩阵分别表示为[11]：

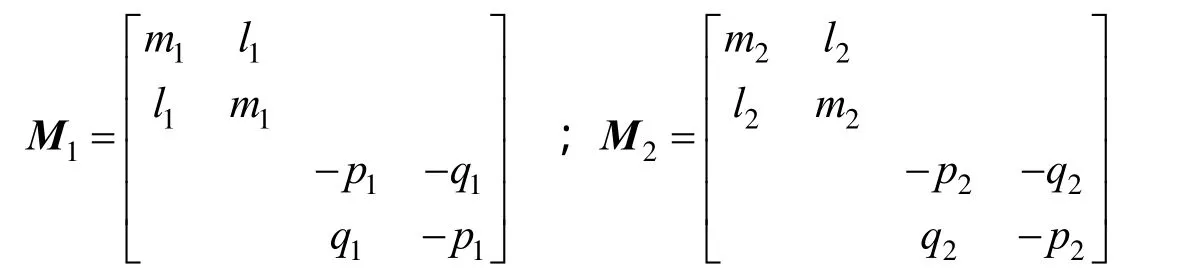
矩阵内部各元素为中间变量，定义为：

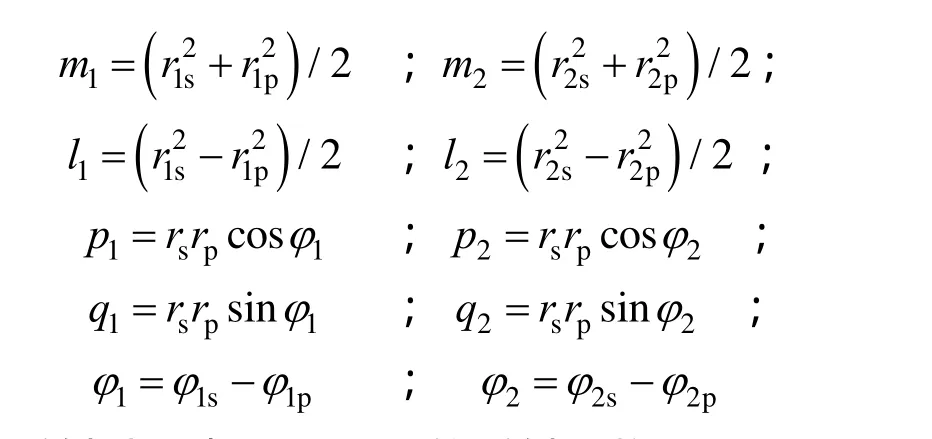
式中 r1s,r1p分别表示第一次反射过程中S、P分量的反射系数，φ1s、 φ1p、 φ1分别表示第一次反射过程中 S、P分量的位相变化以及二者差值； r2s,r2p分别表示第二次反射过程中 S、P分量的反射系数，φ2s、 φ2p、 φ2分别表示第二次反射过程中S、P分量的位相变化以及二者差值。

第一次反射过程的反射光S1为第二次反射过程的入射光S2，根据消偏原理，双反射过程的入射面相互垂直，所以S1的S分量成为S2的P分量，S1的P分量成为S2的S分量，描述这一过程的Mueller矩阵为：

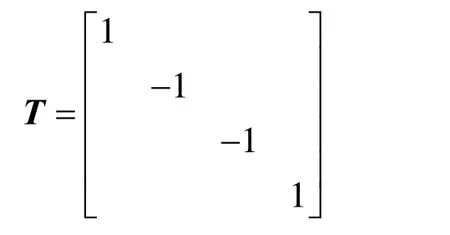
根据偏振光学理论，第一次反射过程可以表示为 S1=M1S0；第一次的反射光到第二次的入射光可以表示为 S2= TS1；第二次反射过程可以表示为 S3=M2S2。于是整个传播过程可以级联表示为[12]：

将Stokes矢量和Mueller矩阵代入式（1）可得：

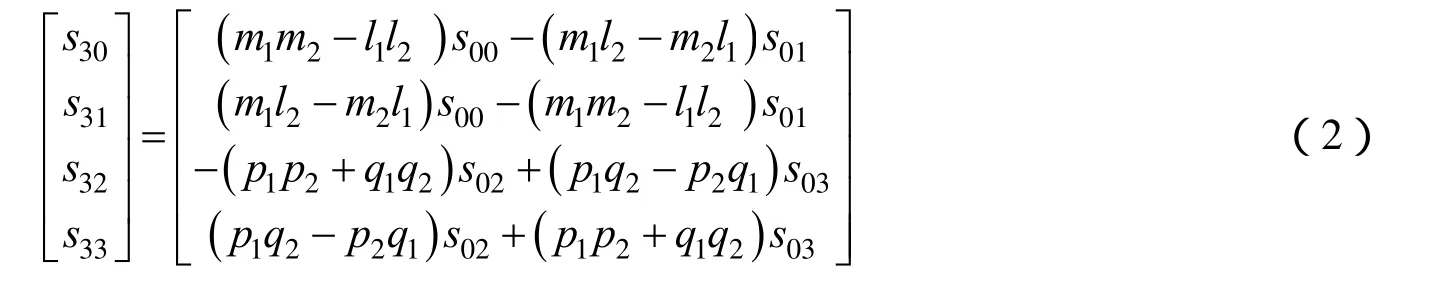
1.3 完全消偏的原理

由于完全消除偏振要求双反射过程的入射角和镜面特性完全相同，其数学表示为：

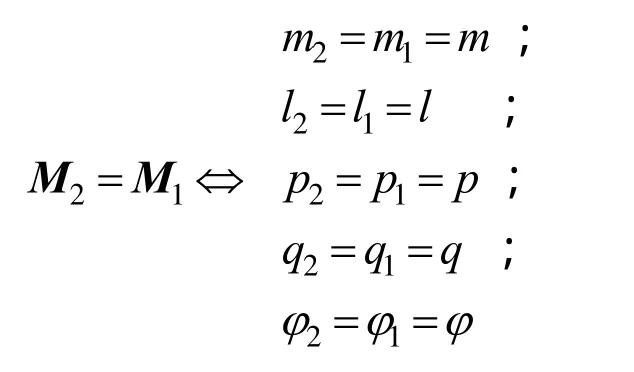
代入到式（2）可得出：

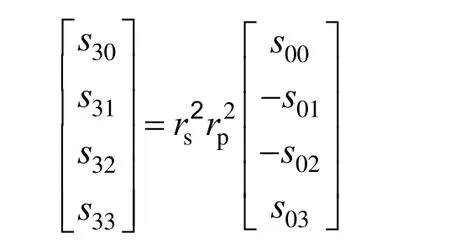
进一步计算可知，输出光的线偏振度PL(S3)、线偏振角 ΦL（S3）、圆偏振度PC(S3)分别与输入光的线偏振度 PL（S0）、线偏振角 ΦL（S0）、圆偏振度 PC（S0）相等13]：

所以输出光与输入光相比，偏振特性没有发生变化，即达到了完全消偏的目的，但是光强衰减了，且输出光与输入光的光强比为：

1.4 导致不能完全消偏的主要因素

但是在实际中，因为各种装调误差、镜面面形曲率、镜面粗糙度、镜面金属膜厚度等因素存在，完全消除偏振几乎不可能。在这些影响因素中，镜面面形曲率、镜面粗糙度、镜面金属膜厚度等因素与生产和加工工艺有关，此类因素固定存在，因此视为次要因素；而装调误差与人为操作的精细程度直接相关，因此视为主要因素。本文在镜面材料确定的前提下，假设次要因素的影响可以忽略，只对主要因素进行讨论。

以第1面反射镜为参考，在理想的装调中，第2面反射镜的所在平面必须与第1面反射镜的所在平面垂直（或正交）；而在实际的装调中，第2面反射镜一般不会正好处于正交位置，定义实际位置与正交位置之间的误差角为σ/2。如果输入45°线偏振光进行检测，即 S0=[1,0,1,0]T，输出光为椭圆偏振光[13]，式（2）化简为：

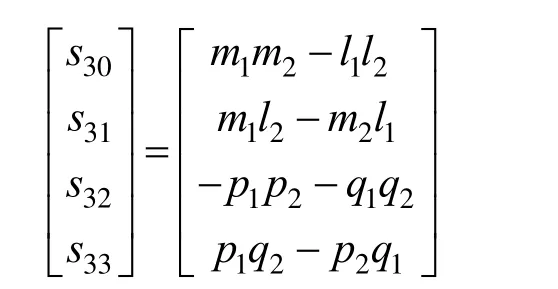
定义 χ为椭圆偏振光的椭圆度，其绝对值描述椭圆率，其正负描述椭圆转向；φ为椭圆偏振光的方位角[14]，则有

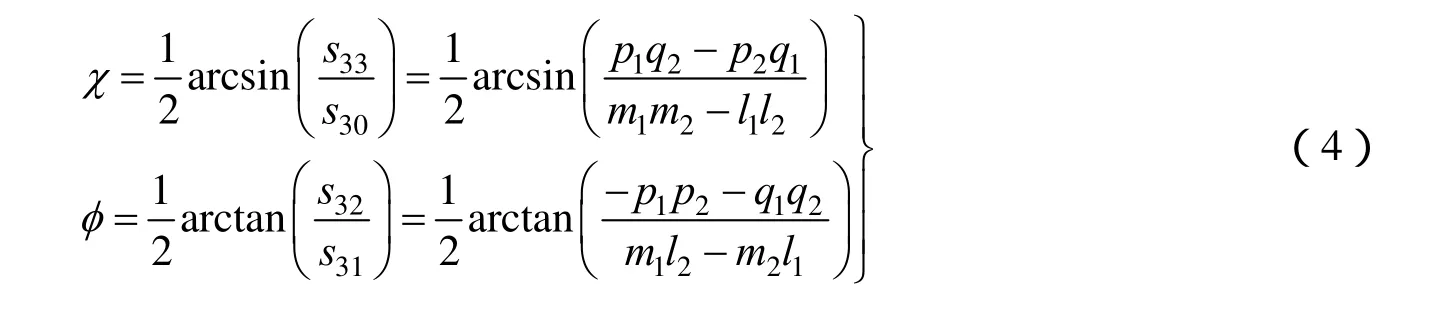
2 仿真分析

以上理论推导对金属镜面双反射消偏过程进行了描述，下面用具体数据进行仿真分析。

参考光线的波长为 589.3nm，反射过程发生在空气与金属的交界处。选取的金属为常用作镜面金属膜材料的五种金属：银、铝、金、铜、汞。其主折射率和主损耗率[15]如表1所示。

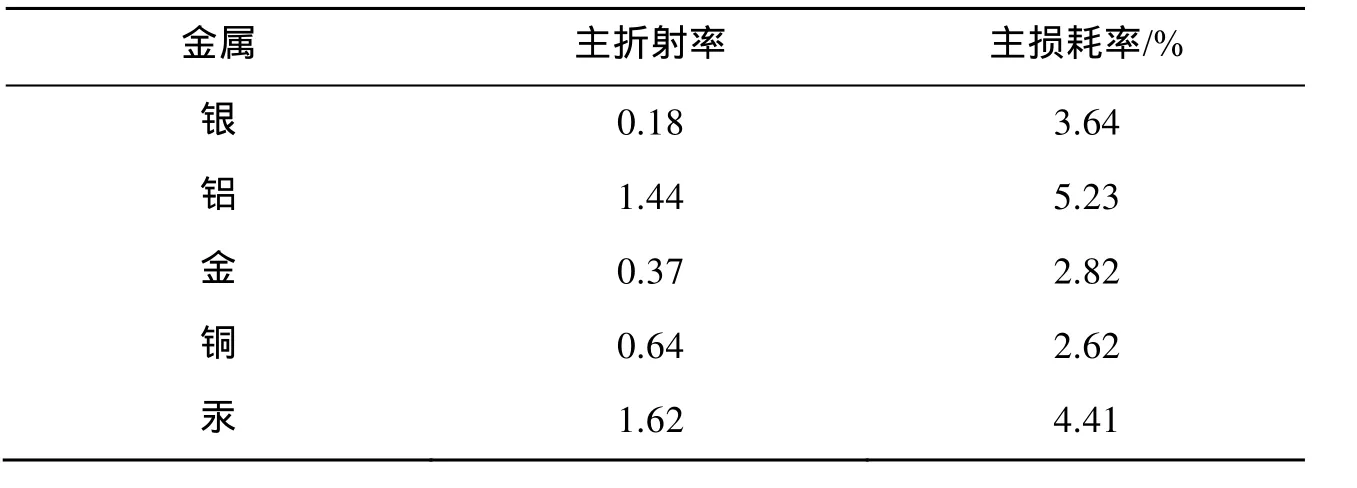
表1 金属的主折射率和主损耗率（λ=589.3nm）Tab. 1 Main refractive index and loss rate of several metals（λ=589.3nm）

1）输入任意状态的光线，入射角0~90°，σ=0°，根据式（3）对输出光与输入光的光强比进行仿真，结果如图3所示。

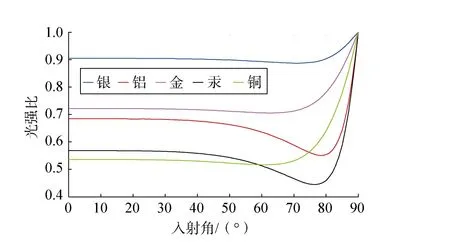
图3 完全消偏时输出/输入光强比率Fig.3 Output/input intensity ratio of polarization eliminated completely

从图3中可以看出，入射角在0~45°之间变化时，五种金属镜面的输出/输入光强比保持稳定，且光强比由高到底分别为银、金、铝、汞、铜；入射角在45~90°之间变化时，五种金属光强比出现不同规律的变化。

2）输入45°的线偏振光，入射角=45°，σ =-1 ~1°，根据公式（4）对输出椭圆偏振光的椭偏特性进行仿真，结果如图4所示。

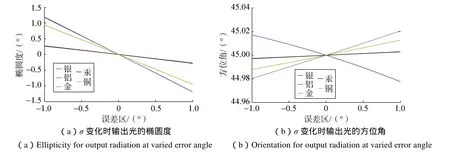
图4 σ变化时输出光的椭圆度和方位角Fig.4 Ellipticity and orientation for output radiation at varied error angle

当σ=0时，椭圆度为0，即输出光为线偏振光，且方位角为45°，等于输入的45°线偏振光的方位，此处达到完全消偏。当σ≠0时，椭圆偏振光的椭圆度和方位角随着σ的增大而增大，即曲线呈线性变化。左图中银和金、铝和汞的重合度较高，右图中铝和汞的重合度较高，这正好体现了两种金属在偏振特性上有相似的特性。此外，图中各条曲线以坐标原点为中心对称分布，这说明在实际装调中，以第 1面镜为参考，第2面镜偏离正交位置的大小要尽可能小，而偏离的方向不是特别重要。

3）输入45°的线偏振光，入射角0~90°，由于据前面分析得出椭偏特性的变化呈中心对称分布，所以此处仅选σ为正的值进行分析，取 σ=1′、10 ′、20 ′，根据式（4）对输出椭圆偏振光的椭偏特性进行仿真，结果如图5所示。

通过对比可以发现，铝和汞的曲线变化规律非常相似，且变化幅度也非常接近。这说明在条件允许的情况下，铝镜可以代替汞镜来使用，或者汞镜可以代替铝镜来使用。银和金的曲线变化规律比较相似，变化幅度金比银略大。铜与其他四种金属的变化规律差异较大。五种金属中，铝和汞在入射角接近 90°的时候，其输出椭圆偏振光的椭圆度发生了很大的变化，这说明，使用铝镜和汞镜时，应当避免入射角太大的情况，或者说入射角太大的时候，不适合用铝镜和汞镜作为双反射消偏装置的镜面材料。银的椭圆度曲线变化为0°~40°左右递增，40°~90°基本不发生变化；金的椭圆度曲线变化为0°~45°左右递增，45°~90°基本不发生变化；铜的椭圆度曲线变化为 0°~80°左右递增，80°~90°基本不发生变化。此外，在入射角不能被限定的情况下，如果要求输出光的椭圆度绝对值保持在0.2左右或者更小，则银镜和金镜的误差角要控制在10′以内，铜镜要控制在5′以内，铝镜和汞镜需控制在1′以内。综合以上分析可以发现，银镜可以保持一个比较大的椭圆度稳定区间，且银镜的椭圆度幅度变化最小，所以银是比较适合作为双反射消偏装置的镜面材料。

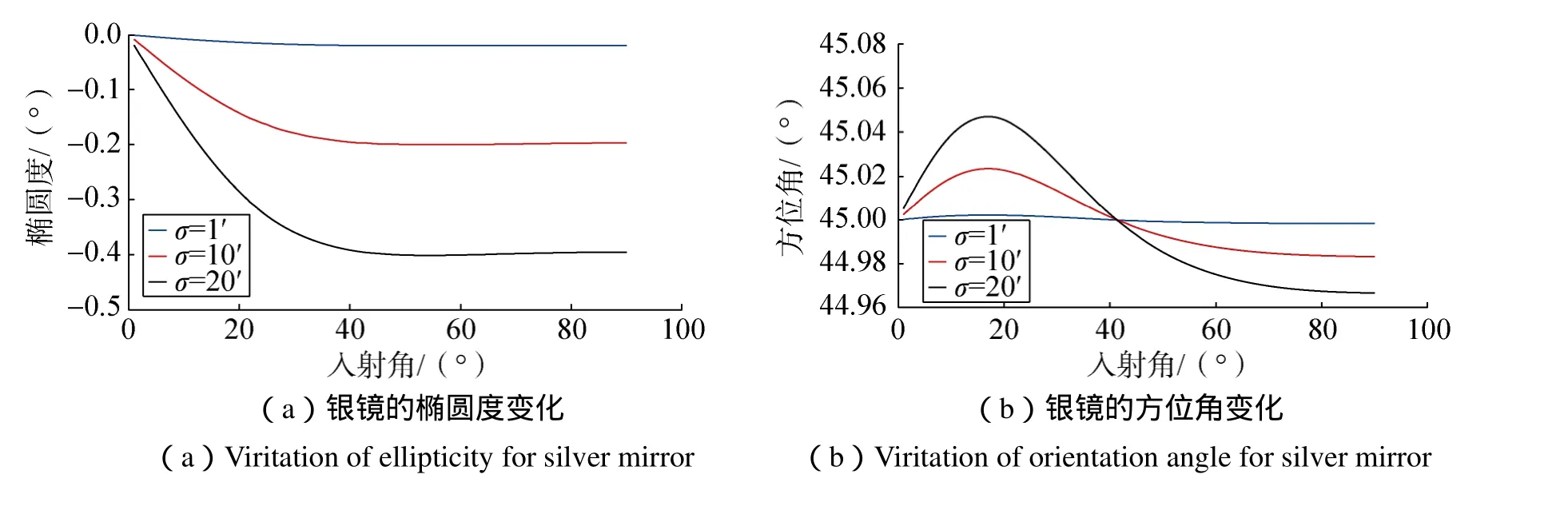
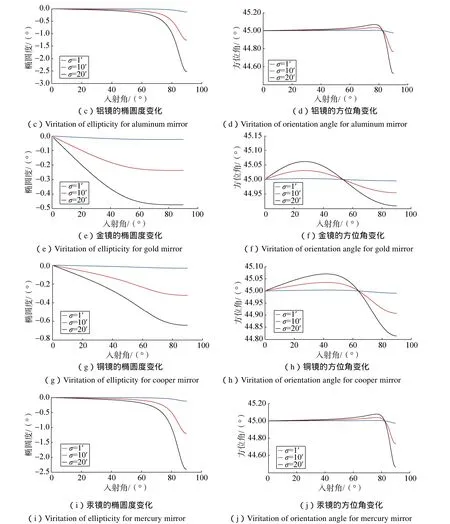
图5 σ固定时输出光的椭圆度和方位角Fig.5 Ellipticity and orientation for output radiation of fixed error angle

3 结束语

文章对金属镜面双反射消除偏振的过程进行了仿真，分析了五种常见金属材料用于该过程时的消偏特性，得出如下结论：

1）银、金、铜在消偏过程中表现出的变化相似，但变化幅度不同；铝、汞在消偏过程中表现出的变化也相似，不同之处也只是变化幅度；但银和铝在消偏过程中的曲线表现不相似。造成这种现象的原因是，银、金、铜的主折射率小于1，而铝、汞的主折射率大于1。

2）主折射率大于1的铝和汞进行对比，两种偏振特性非常相近，但铝对光能的吸收更小，所以铝比汞更适合作为双反射的镜面材料；主折射率小于1的银、金、铜相互对比，银的偏振变化幅度最小，而且银对光能的吸收也最小，所以银比金、铜更适合作为双反射的镜面材料；铝和银相比，当入射角较大（接近90°）的时候，选银更合适，而当入射角较小的时候，选铝更合适。

利用双反射消除偏振的方法，可以有效保持光子的偏振特性，显著提高偏振探测的效率。本文的研究结论为双反射消偏装置的研究提供依据，为偏振补偿的工程应用提供参考。由于实践中还会存在阻碍完全消偏的其他影响因素，所以下一步工作将对双反射消偏的其他因素进行研究。

References)

[1] 赵顾颢, 赵尚弘, 幺周石, 等. 偏振无关的旋光双反射结构的实验研究[J]. 物理学报, 2013, 62(13): 134201-1-134201-5. ZHAO Guhao, ZHAO Shanghong, YAO Zhoushi, et al. Experimental Study on Polarization-independent Reflector Structure Based on Magneto-optical Crystaland Two Mirrors[J]. Acta Phys. Sin. 2013, 62(13): 134201-1-134201-5. ( in Chinese)

[2] 高军, 马骏. 空间光学遥感器系统偏振测试方法探讨[J]. 航天返回与遥感, 1999, 20(2): 17-21. GAO Jun, MA Jun. Investigation of Polarization Measurement for Space Optical Remote Sensor[J]. Spacecraft Recovery & Remote Sensing, 1999, 20(2): 17-21. (in Chinese)

[3] TRAVIS Larry D. Remote Ensing of Aerosols with the Earth Observing Scanning Polarimeter[C]. SPIE, 1992, 1747: 154-164.

[4] CAIRNS Brian, RUSSELLB Edgar E, LAVEIGNEB Joseph D, et al. Research Scanning Polarimeter and Airborne Usage for Remote Sensing of Aerosols[C]. SPIE, 2003, 5158: 33-44.

[5] PERSH Steven, SHAHAM Y J, BENAMI Oren, et al. Ground Performance Measurements of the Glory Aerosol Polarimetry Sensor[C]. Earth Observing Systems XV, SPIE, 2010, 780703: 1-12.

[6] 兰丽艳, 黄颖. 星载大视场多光谱高分辨率CCD相机光学系统的设计[J]. 航天返回与遥感, 2002, 23(4): 34-37. LAN Liyan, HUANG Ying. Optical System Design of Wide-field, Multi-spectral and High-resolution CCD Camera[J]. Spacecraft Recovery & Remote Sensing, 2002, 23(4): 34-37. (in Chinese)

[7] GIL J J, BERNABEU E. A Depolarization Criterion in Mueller Matrices[J]. Optic Acta, 1985, 32: 259-261.

[8] 杨雨迎, 崔占忠, 王玲, 等. 金属目标表面的反射激光偏振特性[J]. 科技导报, 2013, 31(11): 28-32. YANG Yuying, CUI Zhanzhong, WANG Ling, et al. Reflective Laser Polarization Characteristics of Metal Target Surface in the Short-range Detection[J]. Science & Technology Review, 2013, 31(11): 28-32. ( in Chinese)

[9] BASS M, MAHAJAN V N. Handbook of Optics[M]. New York: McGraw Hill Co Inc, 2010.

[10] 陈军. 光学电磁理论[M]. 北京: 科学出版社, 2005. CHEN Jun. Electromagnetic Theory of Optics [M]. Beijing: Science Press, 2005. (in Chinese)

[11] 郁道银, 谈恒英. 工程光学[M]. 北京: 机械工业出版社, 2011. YU Daoyin, TAN Henying. Engineering Optics[M]. Beijing: China Machine Press, 2011. (in Chinese)

[12] 赵佳, 周峰, 李欢, 等. 一种新型的高精度偏振调制技术[J]. 航天返回与遥感, 2014, 35(2): 39-45. ZHAO Jia, ZHOU Feng, LI Huan, et al. Research on New Type of High Precision Polarization Modulation Technology[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(2): 39-45. (in Chinese)

[13] CHIPMAN R A. Metrics for Depolarization[J]. SPIE, 2005, 5888(0L): 1-10.

[14] 谢敬辉, 赵达尊, 阎吉祥. 物理光学[M]. 北京: 北京理工大学出版社, 2005. XIE Jinghui, ZHAO Dazun, YAN Jixiang. Physical Optics[M]. Beijing: Beijing Institute of Technology Press, 2005. (in Chinese)

[15] 马科斯·波恩, 埃米尔·沃尔夫. 光学原理[M].杨葭荪, 译. 北京: 电子工业出版社, 2009. MAX Born, EMIL Wolf. Principles of Optics[M]. Translated by: YANG Jiasun. Beijing: Publishing House of Electronics Industry, 2009. (in Chinese)