基于稀疏孔径的波前重构算法

王棪 伏瑞敏 廖志波

（北京空间机电研究所，北京 100094）

0 引言

随着对高分辨率遥感数据需求的迫切性，增大光学遥感器口径是满足需求的有效手段。而口径增大带来了一系列设计、装调与检测问题，其中大口径光学系统检测是检验装调精度的关键环节，同时也是指导装调的重要手段，在遥感器光学系统研制过程中具有重要作用。

在大口径光学系统检测过程中，一般利用干涉仪和大口径标准平面镜组成自准直光路，检测镜头波像差。大口径标准平面镜作为参考标准镜有两方面要求：1）口径要大于待测镜头入瞳直径，以实现全口径全视场测试[1-3]；2）对表面精度有极高的要求[4-5]。随着相机口径的逐渐增大，系统测试所使用的标准平面镜的口径也随之增大，大口径平面镜制造的难度和成本也随之呈指数级提高。为了保障大口径、超大口径相机装调的顺利实施，在传统的全口径检测手段之外，发展低成本、高效的替代检测方案成为必需的选择。子孔径拼接和稀疏孔径反演是解决大口径光学系统检测的两种主要方案。

子孔径拼接虽然只需要一块小口径平面镜[6-8]，但是该技术需要复杂的运动机构，同时测试周期长，效率低，易受到环境的影响。因此，基于测试复杂程度、成本以及兼容性考虑，采用稀疏孔径反演的光学系统检测技术成为较优选择。例如，预计于2018年发射的詹姆斯·韦伯望远镜，口径达6.5m，通过对多种检测方案的评估，研究团队最终采用稀疏孔径反演检测技术[9-14]；通过大量仿真分析和实验研究，使得该技术的可行性在相机上得到验证。国内尚无该项技术应用于大口径光学系统装调检测的研究，仅有针对大口径元件面形检测以及大口径光学系统 MTF测试的一些理论研究[15-16]。当前，我国大口径光学遥感器的需求方兴未艾，大口径光学系统波前检测技术的瓶颈亟待突破，因此开展稀疏孔径检测技术研究极具工程价值。本文从稀疏孔径检测光学系统波前的原理入手，针对波前重构算法建立数学模型，并编制了相关算法，最后利用仿真手段进行了分析和验证，通过比对稀疏孔径和全口径两类检测模型测得的Zernike多项式系数和波像差RMS值，证明了算法的可行性。

1 波前重构算法

1.1 稀疏孔径检测

稀疏孔径反演是一种基于自准直检测的技术，通过搭建由干涉仪、待测光学系统、标准反射镜构成的光路检测光学系统的波像差，波像差由Zernike多项式表征[17-18]。根据Zernike多项式系数计算光学系统失调量以指导装调，其独到之处在于采用若干块小口径平面反射镜替代一块大口径平面反射镜，按照一定的结构进行排列、安装组成稀疏孔径阵列。采用稀疏孔径阵列检测反射式光学系统的波像差（如图1），干涉仪发出球面波通过光学系统次镜、主镜变为平面波，经稀疏孔径阵列反射后回到干涉仪并与参考光形成干涉。采用该技术的优点是：1）与子孔径拼接相对比，无需多次调整、检测，只需在检测前安装调整各反射镜进行一次检测，检测效率得到明显提升，且可降低时变因素的干扰；2）避免了制造大口径标准镜所带来的高昂成本、技术风险。由于稀疏孔径阵列并未覆盖全口径，因此采集的信息不完整，需要对检测结果进行处理以重构整个全口径的波像差。因此，实现波前（或波像差）重构是稀疏孔径反演技术的关键。本文提出的算法，解决的正是如何由若干组子孔径的Zernike系数计算全口径Zernike系数的问题。

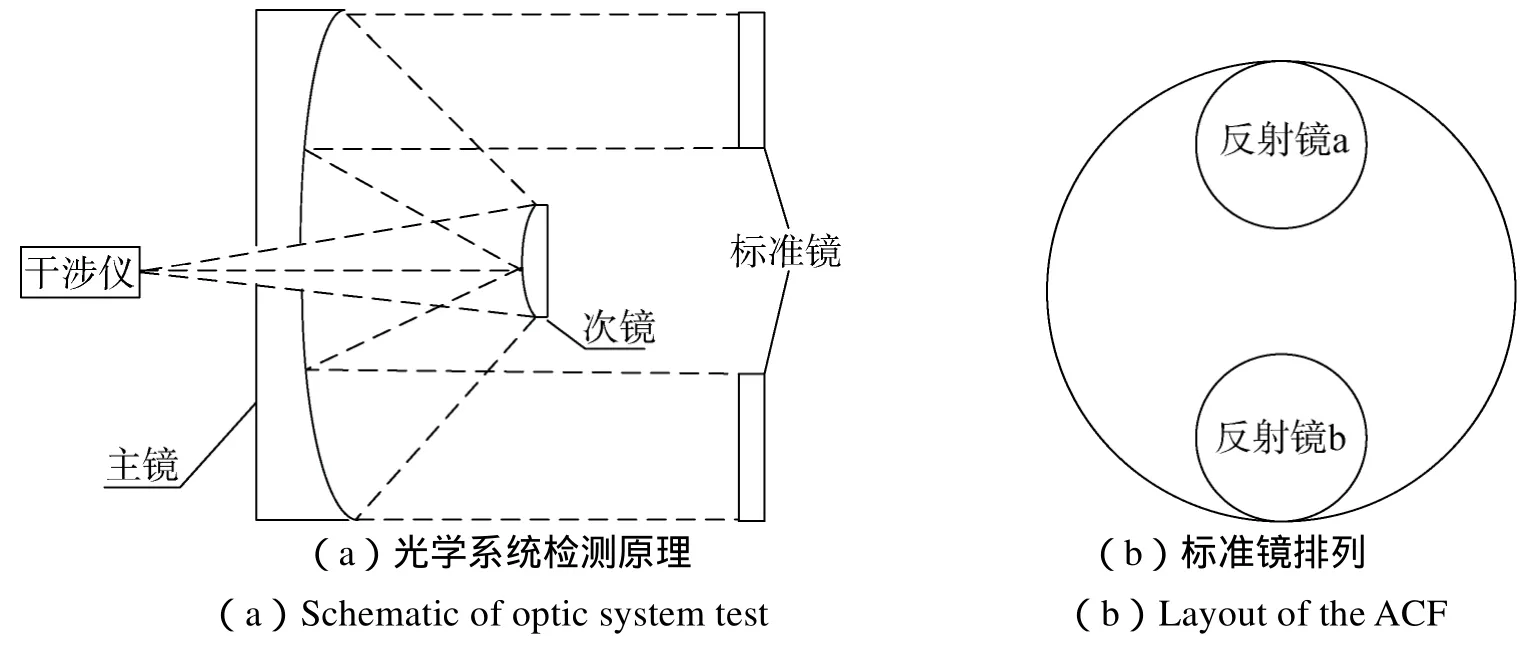
图1 稀疏孔径原理Fig.1 The schematic of sparse aperture

1.2 算法数学模型

采用常规手段和稀疏孔径反演检测光学系统波像差，实质上都是一个利用采集到的离散点光程差拟合光学系统波像差函数的过程，但两种手段在数据采集和处理方法上存在不同。采用常规的全口径标准镜检测，是针对全口径进行数据采样，得到分布于整个光瞳内若干点的光程差，同时，在以全口径中心O为原点的坐标系下（如图2），任一采样点Q对应坐标（x，y），根据若干采样点的坐标值和光程差值通过一定算法拟合得到 Zernike多项式表征的波像差函数，即直接得到光学系统的波像差；采用稀疏孔径检测，由于标准镜不再是一块覆盖全口径的标准镜，而是若干小口径的反射镜，因此只在各反射镜覆盖到的区域内进行数据采集和处理，对于任意一个反射镜对应的子孔径（如图3），采集该子孔径区域内的若干点的光程差，同时，在以子孔径区域中心O'为原点的坐标系下，任一采样点Q'对应坐标（x'，y'）。根据若干采样点的坐标和光程差值拟合得到该子孔径的波像差函数。因此，常规的全口径检测得到的是全口径的波像差，而对于由多块反射镜组成的稀疏孔径阵列，对多个子孔径进行采样，检测得到的是各个反射镜对应的若干子孔径的波像差函数，而不是整个光学系统的波像差。因此，需要将各子孔径波像差函数统一至同一坐标系，把多组子孔径Zernike系数转化为一组全口径Zernike系数，从而得到由Zernike多项式表征的波像差函数，实现光学系统波像差重构。

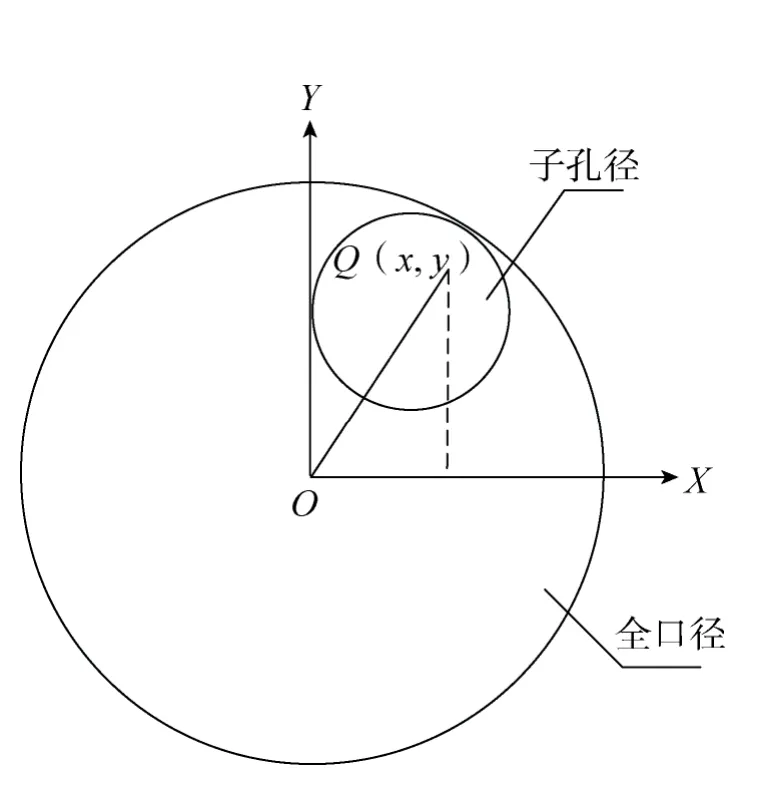
图2 全口径坐标系Fig.2 Coordinate system of full aperture

图3 子孔径坐标系Fig.3 Coordinate system of sub-aperture

本文算法采用Fringe Zernike多项式对波像差进行描述，该多项式是标准形式的子集，其每一项有明确物理含义对应不同的像差，包括初级像差和高级像差。由于装调只考虑初级像差，因此取初级像差的对应项（见表1）构成多项式描述波像差，则光学系统的波像差函数可表示为

式中 (ρ,)θ表示为采样点极坐标；W(ρ,)θ表示波像差；n为多项式项数；cn表示Zernike多项式第n项系数；Zn表示Zernike多项式（详见表1）。子孔径与全口径间的Zernike系数转换即在式（1）的基础上进行。

首先考虑单个子孔径和全口径间的Zernike系数的关系，在以全口径中心O为原点的全口径坐标系下（如图2），全口径波像差为

表1 Zernike系数对应的初级像差Tab.1 Primary aberration corresponding to Zernike coefficients

在以子孔径中心O'为原点的子孔径坐标系（如图3）下，子孔径波像差为

式中 (ρ′,θ′)为采样点在子孔径坐标系下的极坐标；W ′(ρ ′,θ′)表示子孔径波像差；为子孔径Zernike多项式系数；为子孔径Zernike多项式。对于子孔径内的任意一点Q，其光程差在两个坐标系下对应的值是恒定的，因此有

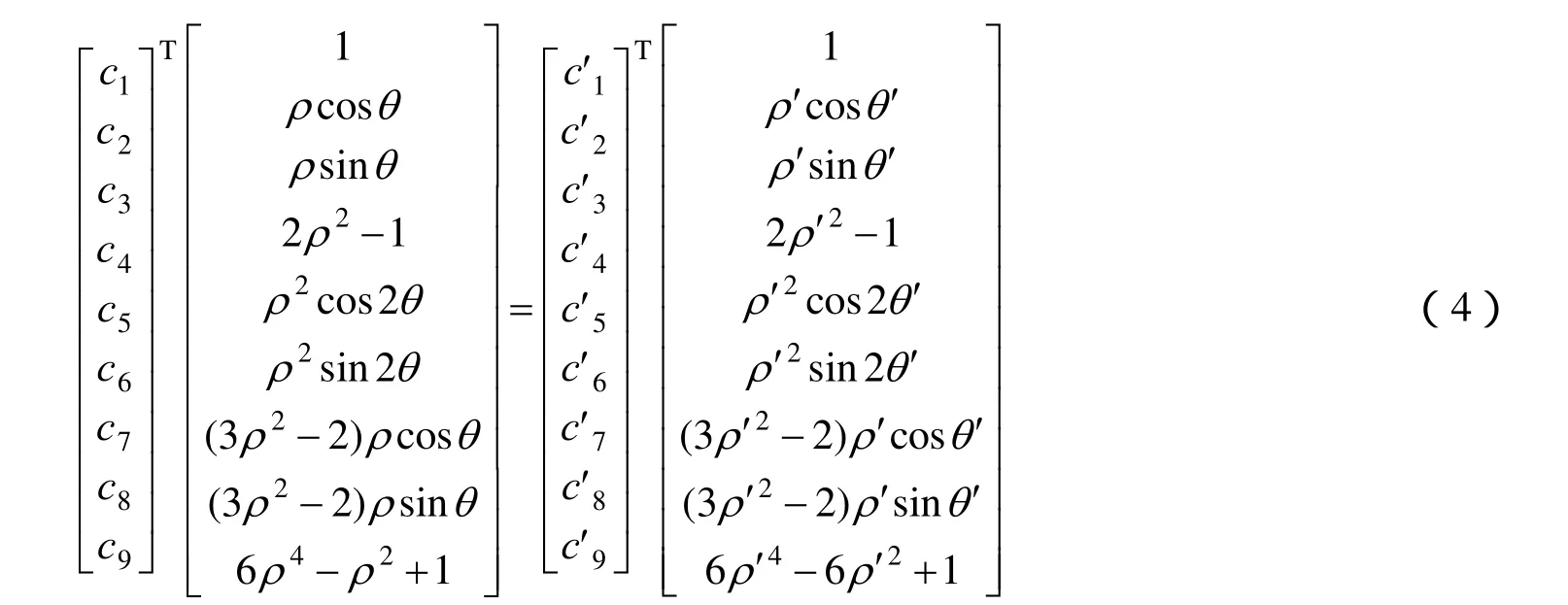
结合波像差和Zernike多项式理论推导，可得矩阵k，使得式（5）成立，

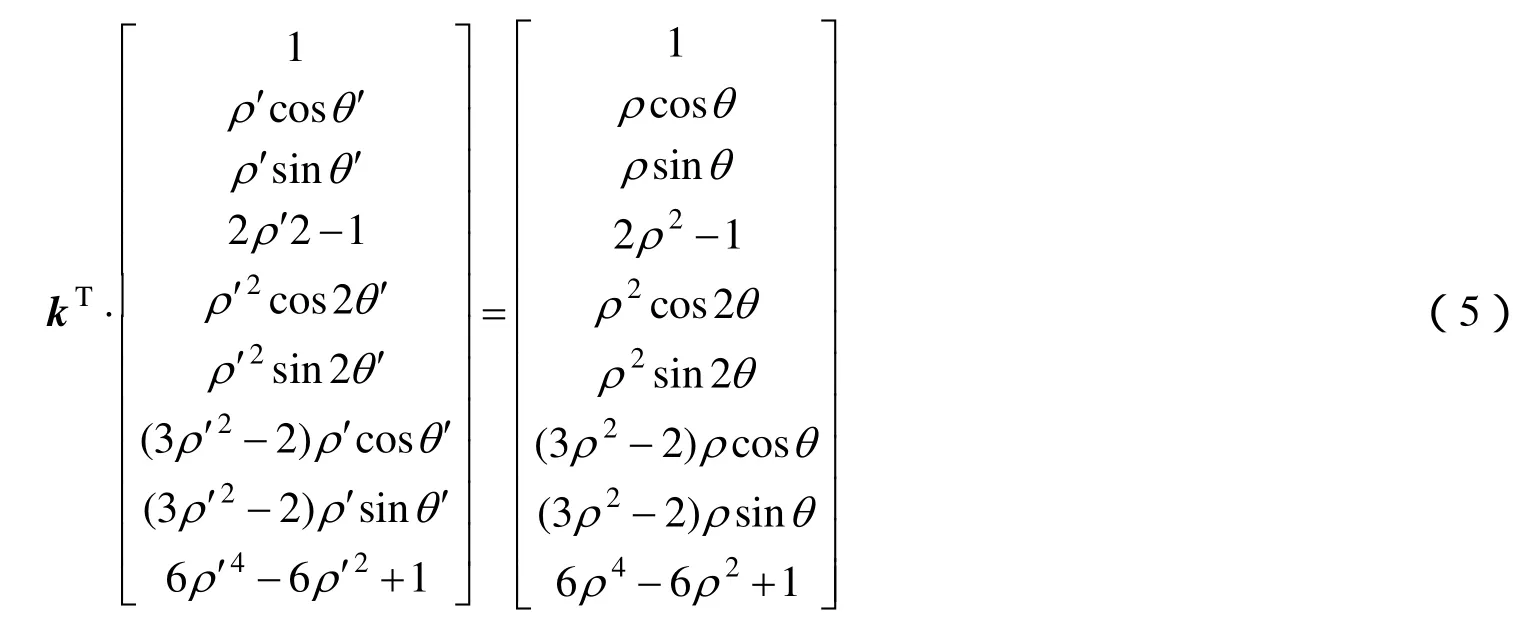
结合式（4）~（5），全口径Zernike系数与单个子孔径Zernike系数间存在关系：

式中 矩阵k为坐标系的转换因子。

稀疏孔径阵列由若干反射镜构成，对应多个子孔径，因此在式（6）的基础上可构建多个子孔径与全口径间的Zernike系数转换关系。假设稀疏孔径含m块反射镜，建立方程：

每个子孔径对应一个转换因子 ki（i∈[1，m]）以及一组Zernike系数矩阵Ci（i∈[1，m]），Ci包含对应子孔径的9项Zernike系数，由若干反射镜对应的ki、Ci组成矩阵K和C。式（7）中Zernike系数矩阵c，包含9个未知数，其求解流程为：1）检测若干块反射镜对应的子孔径波像差，得到包含若干组Zernike系数的矩阵C；2）计算各反射镜对应的转换因子ki，组成包含若干组转换因子的变换矩阵K；3）建立方程，求解全口径Zernike系数矩阵c。

上述算法的实现是建立在稀疏孔径的误差（包括平移和倾斜）得到有效控制的基础之上，因此，实际应用中，需首先将各反射镜的平移和倾斜控制在可接受范围内，减小误差对计算精度的影响。控制误差方法主要包括：以大口径参考球面镜或者抛物镜为基准（即参考镜保持不动），对稀疏孔径阵列的各反射镜进行调整，使单个子孔径的平移、倾斜分量控制在可接受范围内。而对于离焦，由于检测光学系统的是平面镜阵列，其相互间的离焦很小，可以忽略不计。

本算法是一种针对大口径光学系统装调的复原全口径波像差方法，当待测系统口径达到m级以上，采用稀疏孔径技术进行检测，有望在规避诸多技术风险的同时高效地解决问题。

2 仿真及分析

2.1 仿真模型

本文采用的稀疏孔径检测模型按照反射镜数量分为3ACF（auto-collimating flat）结构和4ACF结构。根据转换因子k和光学系统的遮拦大小进行分析计算，当子孔径和全口径半径的比值为0.33（子孔径半径为533mm）和0.39（子孔径半径为 635mm）时计算精度较高。按照子孔径相对位置和半径大小，将3ACF和4ACF结构再分别细分为三种构型，如图4~5所示。图中大圆表示全口径，小圆表示稀疏孔径阵列各反射镜对应的子孔径，所有结构均为对称结构，各子孔径对称地分布于全口径内。

对于3ACF结构：结构1与结构2子孔径半径相同，为533mm，其中结构1的各子孔径与全口径相切，结构2的子孔径间相对距离更近；结构3中的子孔径半径为635mm，各子孔径与全口径相切。4ACF结构的3种构型与3ACF结构的类似，反射镜数量增加为4个。

图4 3ACF结构Fig.4 3ACF structure

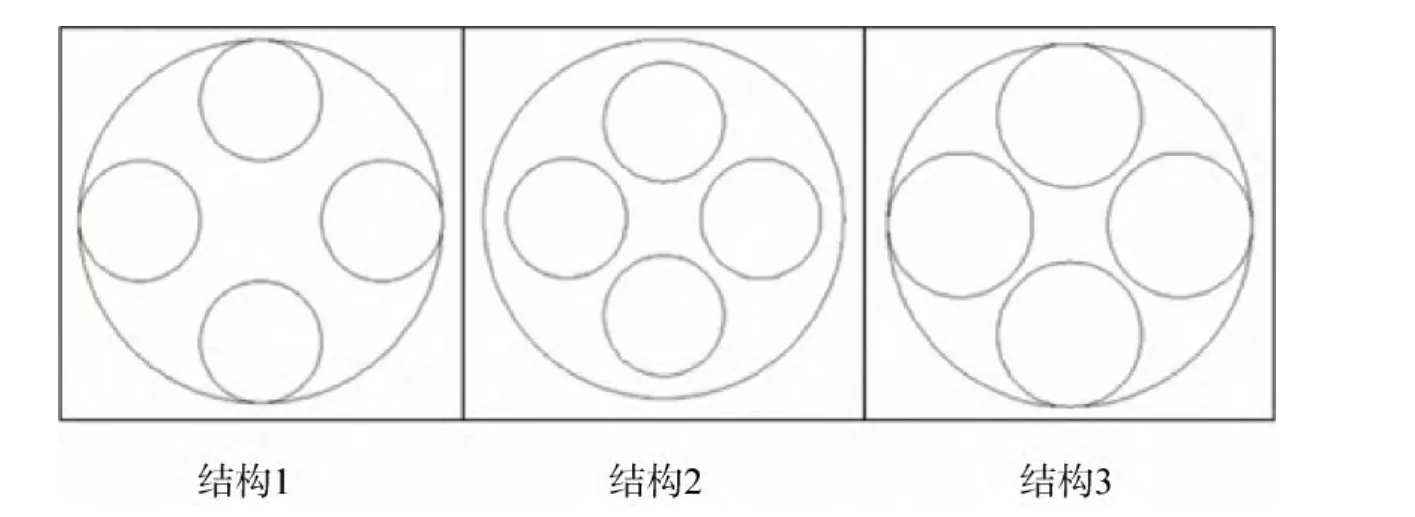
图5 4ACF结构Fig.5 4ACF structure

利用光学软件和MATLAB建模分析某口径为3.2m的反射式光学系统的波像差，验证算法可行性。首先建立如图6所示的全口径检测模型，为光学系统加入失调误差，进行全口径检测，提取Zernike系数中初级像差的对应项。全口径检测完成后，建立多种不同结构的稀疏孔径检测模型（图7为一种包含三块自准直镜的稀疏孔径阵列检测模型），分别对光学系统进行波像差检测。利用算法由检测得到的各反射镜对应的子孔径Zernike系数推导全口径Zernike系数。将两种方法得到的全口径系数进行对比，然后由计算得到的全口径Zernike系数反演全口径波像差，并与全口径直接测得的波像差RMS值进行对比，若差值在 0.001λ（λ=656nm，为波长）以内，则算法满足精度要求。同时若各种结构其重构精度存在差异，则需分析其重构精度差异性的原因。检测过程中，忽略各反射镜、标准平面镜的面形以及稀疏孔径的结构误差。

图6 全口径检测Fig.6 Full aperture test

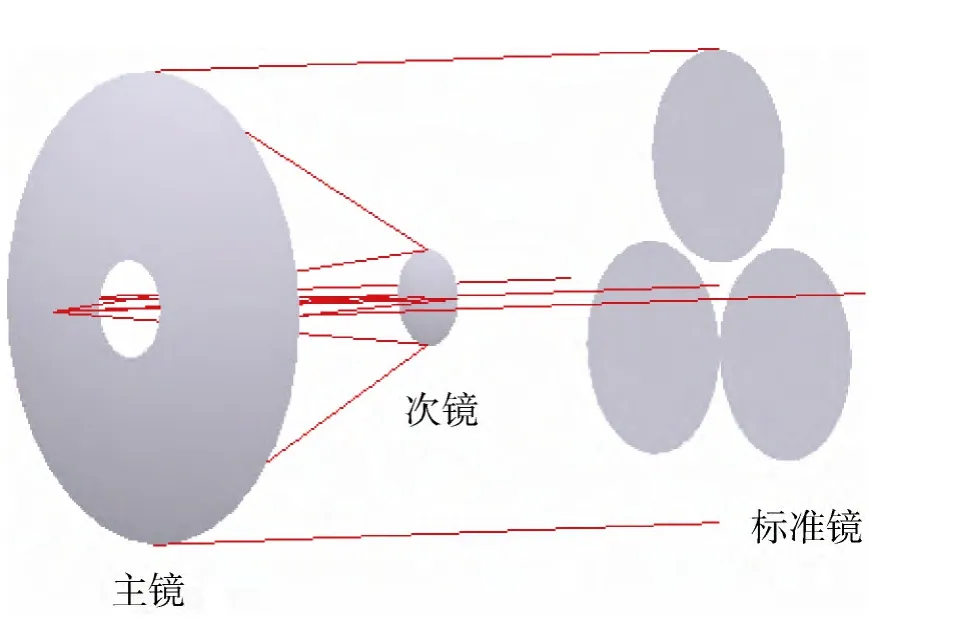
图7 稀疏孔径检测Fig.7 Sparse aperture test

2.2 仿真结果及分析

依据图4~5所示的稀疏孔径结构建模，对光学系统波像差进行检测。

2.2.1 3ACF结构

首先建立全口径检测模型，对光学系统进行波像差检测，获取全口径 Zernike系数，然后分别采用三种3ACF结构对光学系统进行波像差检测，提取各结构中若干子孔径的Zernike系数，经过算法处理得到全口径Zernike系数，对比三种稀疏孔径结构测试和全口径测试得到的Zernike系数。由于本算法针对的是光学系统装调，光学系统失调量是利用像散、慧差、球差对应的五项 Zernike系数进行解算的，因此本文着重对这几项Zernike系数进行分析。图8为多项式项数为4~9项时三种结构计算得到的Zernike系数与直接测得的全口径Zernike系数的差值曲线。由图8可看出，三种结构的重构精度存在差异，其中结构3对应的系数与全口径系数最为接近。

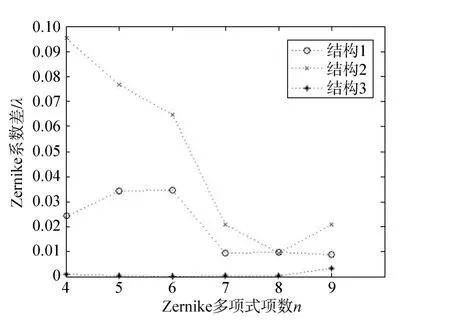
图8 Zernike系数对比Fig.8 Comparison of Zernike coefficients

根据测得的Zernike系数反演全口径波像差，三种结构以及全口径对应的波像差RMS如表2所示。

表2 3ACF结构对应的波像差RMS值Tab.2 RMS of 3ACF structure

结合图8和表2可知，三种构型中结构3的波像差RMS值与全口径差值小于0.001λ，满足算法精度要求。对比结构 1与结构 2，两者重构精度因各反射镜相对位置不同而存在差异；同理，对比结构 1与结构3发现，反射镜的口径同样对重构精度存在影响。因此，波前重构算法的重构精度受反射镜的口径和相对位置的影响。

2.2.2 4ACF结构

分别采用图7所示的三种4ACF结构建模对光学系统进行波像差检测，获取全口径Zernike系数，然后分别采用三种4ACF结构对光学系统进行波像差检测。三种结构对应的Zernike系数差值曲线如图9所示，该图显示结构3与全口径值差异最小。

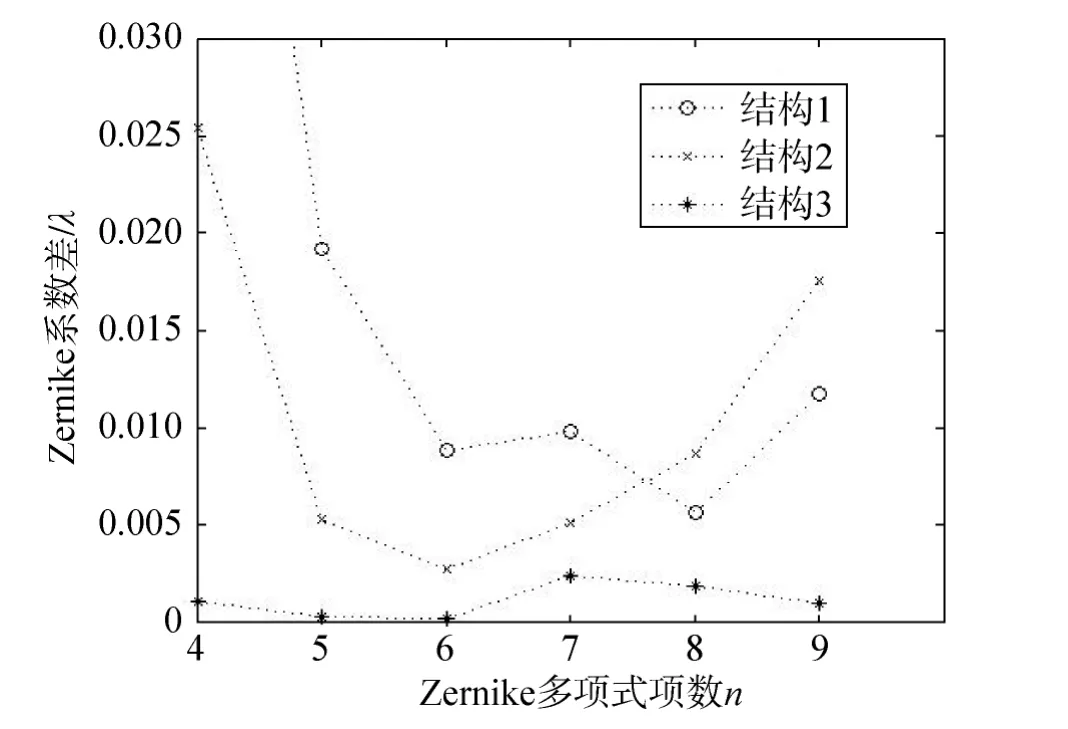
图9 Zernike系数对比Fig.9 The comparison of Zernike coefficients

根据算法处理得到的三种结构对应的 Zernike系数反演全口径波像差，并与直接测得的全口径波像差RMS进行对比，结果见表3。

表3 4ACF结构对应的全口径波像差RMS值Tab.3 RMS of 4ACF structure

由表3可知，结构3对应RMS差值小于0.001λ，满足精度要求。与3ACF结构类似，4ACF结构的各对照组也显示出重构精度的差异，反射镜的口径大小和反射镜间的相对位置均会对重构精度造成影响。

2.2.3 对比分析

对上述仿真结果进行综合比对发现，利用算法重构全口径波像差是可行的，但并非所有结构都能满足精度要求，各个结构的区别在于反射镜数量、口径大小、相对位置，因此，检测特定的光学系统，首先需结合待测系统指标进行分析，明确稀疏孔径反射镜数量、口径、间距，根据这些指标选取合适的反射镜搭建、调整稀疏孔径结构使之与待测系统匹配，然后再对光学系统进行检测。

就本文研究的几种结构而言，3ACF的结构3和4ACF的结构3均具有较高的重构精度，而在实际使用中，为了缩短稀疏孔径阵列安装的时间，提高效率，稀疏孔径阵列的反射镜数量越少越好，因此，对于该光学系统而言，采用3ACF的结构3作为稀疏孔径阵列是最佳方案。

3 结束语

在未来的空间遥感领域，大口径光学系统将会得到更多的应用，因此研制大口径光学系统是当下的一个重要课题，同时为保证光学系统具有良好的成像品质，有必要发展和建立一套完善的地面波前检测方法。本文以大口径光学系统装调检测作为切入点，提出了一种可行的稀疏孔径波前重构算法，用以实现由若干子孔径波前重构光学系统波前，是解决常规手段所面临的效率、成本、技术风险等难题的一种新思路。采用若干反射镜组成稀疏孔径标准镜取代单块的全口径反射镜，降低了制造加工的成本和周期以及潜在的技术风险，同时也无需多次检测，提升了效率，该技术是突破大口径光学系统装调技术瓶颈的一种有效途径。

References)

[1] 李林. 现代光学设计方法[M]. 北京: 北京理工大学出版社, 2009. LI Lin. Modern Optic Design Method[M]. Beijing: Beijing Institute Technology Press, 2009. (in Chinese)

[2] 史亚莉, 高云国, 邓伟杰. 反射光路的计算机辅助装调模型[J]. 激光与红外, 2009, 39(4): 427-430.SHI Yali, GAO Yunguo, DENG Weijie. Model for Computer-aided Alignment of Reflective Optic System[J]. Laser&Inflared, 2009, 39(4): 427-430. (in Chinese)

[3] 孙敬伟, 陈涛. 主次镜系统的计算机辅助装调[J]. 光学精密工程, 2010, 18(10): 2156-2162. SUN Jingwei, CHEN Tao, Computer-aided Alignment for Primary and Secondary Mirrors[J]. Optic and Precision Engineering, 2010, 18(10): 2156-2162. (in Chinese)

[4] 李晓彤, 岑兆丰. 几何光学·像差·光学设计[M]. 杭州: 浙江大学出版社, 2014. LI Xiaotong, CEN Zhaofeng. Geometrical Optics, Aberrations and Optical Design[M]. Hangzhou: Zhejiang University Press, 2014.

[5] 徐德衍. 现代光学元件检测与国际标准[M]. 北京: 科学出版社, 2009. XU Deyan. Modern Optical Components Test and International Standard[M]. Beijing: Science Press, 2009.

[6] 汪利华, 吴时彬, 侯溪, 等. 子孔径拼接干涉检测大口径平面波前[J]. 光电工程, 2009, 36(6): 126-130. WANG Lihua, WU Shibin. Measurement of Flat Wavefront by Sub-aperture Stiching Interferometry[J]. Opto-Electronic Engineering, 2009, 36(6): 126-130. (in Chinese)

[7] 侯溪, 伍凡, 杨力, 等. 子孔径拼接干涉测试技术现状及发展趋势[J]. 光学与光电技术, 2005, 3(3): 50-53. HOU Xi, WU Fan. Status and Development Trend of Sub-aperture Stiching Interferometric Testing Technique[J]. Optics & Optoelectronic Technology, 2005, 3(3): 50-53. (in Chinese)

[8] Didier Castel, Emmanuel Sein, Dr. Takao Nakagawa. The 3.2m all SiC Telescope for SPICA[C]. Conference on Modern Technologies in Space- and Ground-based Telescopes and Instrumentation II. Amsterdam(NL): SPIE, 2012.

[9] Sabelhaus P A, Campbell D, Clampin M, et al. An Overview of the James Webb Space Telescope (JWST) Project[C]. UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts II. San Diego, CA: SPIE, 2005.

[10] Barto A A, Atkinson C, Contreras J. Optical Performance Verification of the James Webb Space Telescope[C]. Conference on Space Telescopes and Instrumentation. Marseille, France: SPIE, 2008.

[11] Guillaume A, Terrile R J, Allmen P V. Fine Alignment of the James Webb Space Telescope with a Genetic Algorithm[C]. IEEE Aerospace Conference. Big Sky, Montana, USA: IEEE, 2009.

[12] Knight J S, Lightsey P, Barto A. Verification of the Observatory Integrated Model for the JWST[C]. SPIE Conference on Modeling, Systems Engineering, and Project Management for Astronomy. San Diego, California: SPIE, 2010.

[13] Howard J M, Hayden B, Keski-Kuha R. Optical Modeling of the Alignment and Test of the NASA James Webb Space Telescope[C]. 2007 IEEE Aerospace Conference. Big Sky, MT, USA: IEEE, 2007.

[14] Atkinson C, Harrison P, Matthews G, et al. Integration and Verification of the James Webb Space Telescope[C]. Optical manufacturing and testing. Bellingham, WA: SPIE, 2003.

[15] 闫锋涛, 范斌. 稀疏子孔径采样检测大口径光学器件[J]. 强激光与粒子束, 2011, 23(12): 3193-3196. YAN Fengtao, FAN Bin. Large Aperture Mirror Testing Using Sparse Sub-aperture Sampling[J]. High Power Laser and Particle Beams, 2011, 23(12): 3193-3196. (in Chinese)

[16] 郑旭, 任智斌. 大口径光学系统光学传递函数测量技术研究[D]. 哈尔滨: 哈尔滨工业大学硕士论文, 2013. ZHENG Xu, REN Zhibin. Research on MTF Measurement of Large Aperture optical system[D]. Harbin: Master’s Thesis of Harbin institute of technology, 2013. (in Chinese)

[17] D·马拉卡拉.光学车间检测[M]. 杨力, 伍凡, 等. 北京: 机械工业出版社, 2012. Daniel Malacala. Optical Shop Testing[M].YANG Li, WU Fan, et al. Beijing : China Machine Press, 2012. (in Chinese)

[18] 单宝忠, 王叔岩. Zernike多项式拟合方法及应用[J]. 光学精密工程, 2002, 10(3): 318-322. SHAN Baozhong, WANG Shuyan. Zernike Polynomial Fitting Method and Its Application [J]. Optics and Precision Engineering, 2002, 10(3): 318-322. (in Chinese)