基于神经网络杂交模型的降落伞动态应力补偿方法

罗韬 庄毅

基于神经网络杂交模型的降落伞动态应力补偿方法

罗韬 庄毅

（南京航空航天大学计算机科学与技术学院，南京 210016）

文章以小型平面圆形伞为原型，根据伞衣初始充气过程中的计算流体力学与结构动力学的耦合模型，引入神经网络杂交建模的思想；提出降落伞开伞过程中伞衣动态应力测量的补偿方法；使用静态样本数据，对跌落、风洞动态试验中采集到的动态应力样本进行补偿计算。计算结果表明：应力补偿方法较准确地反映瞬态伞衣应力变化情况，具有收敛性和有效性，对降落伞设计具有参考意义；与传统的神经网络补偿方法相比，神经网络杂交模型能够显著提高补偿精度，且具有更小的计算规模和更快的收敛速度。

应力补偿 神经网络 杂交模型 降落伞

0 引言

降落伞作为柔性织物，具有几何非线性与材料非线性并存的大变形结构动力学行为；伞衣内外的流场十分复杂：内部流动是显著的湍流状态，外部则存在着严重的分离现象，同时还有部分气流透过织物；织物的结构变形与周围的流场变化的相互耦合也十分复杂，变形、透气性影响了伞衣周围压力场的变化，而压力场的变化反过来又对伞衣形状产生影响。因此，降落伞初始充气过程是一个多阶段的刚柔耦合动力学问题，难以直接通过系统仿真评估工作过程各个阶段的受力情况，也难以通过一般的地面和空投试验得到各种工况下充气过程中降落伞伞衣、绳体和径向带的静态、动态应力数据。

近年来，在气动力学和结构力学基础上建立起来的CFD（computational fluid dynamics）-MSD（mass spring damper）耦合模型[1-2]，较好地反映降落伞所受的气动弹性力本质，但透气量、弹性系数及阻尼系数的不确定性是其缺陷所在。T. Tezduyar教授对十字型伞、密实织物伞的流固耦合计算问题进行了深入研究，提出了伞衣结构几何透气性的建模方法[3-4]。Takizawa等人用稳定空域流固耦合法计算了降落伞稳降时的结构和流场情况，但没有计算完整的开伞过程[5-7]。Tutt使用LS-DYNA有限元仿真软件建立流固耦合模型，用于标定降落伞真实试验数据，但没有考虑伞衣应力变化[8]。余莉等人采用任意拉格朗日-欧拉法（Arbitrary Lagrange Euler method，ALEM）成功模拟某模型伞在低速气流作用下充气展开过程，但仅通过仿真计算来获得了充气过程中伞衣应力、流场速度矢量、压力以及伞衣半径变化等数据，没有进行真实试验测量[9-10]。连亮在群伞研究中引入流固耦合方法，但没有模拟群伞的整个开伞过程[11]。

神经网络具有逼近任意的非线性函数的能力，在复杂未知的非线性系统建模中被广泛应用。它属于一种黑箱建模方法，不用考虑系统先验知识，直接利用样本训练来描述系统的非线性动力学特性，能够较好地逼近传感器输入—输出之间的非线性映射关系。Taib和Dempsey使用神经网络来进行传感器的非线性校正[12-13]，Pasquale等采用神经网络来消除传感器误差[14]，Tian采用递归神经网络来建立传感器非线性模型[15]，但传统神经网络通常网络规模较大，网路训练周期较长，且可能收敛至局部最小值，泛化能力较差。

本文采用神经网络对非线性传感器系统进行逆向建模，实现对降落伞开伞过程中应力传感器采集到的动态应力进行补偿。鉴于传统神经网络的缺陷，将神经网络杂交建模的思想引入到应力传感器输入-输出非线性映射关系的标定过程中，并采用主成分分析的方法对样本数据进行降维处理，然后结合静态、动态试验中传感器采集到的样本数据展开研究。试验证明，该方法不仅能够有效地补偿伞衣应力数据，而且补偿精度和可靠性也得到了保证。

1 非线性补偿原理

不失一般性，假设传感器的非线性模型可以表示为

式中 y表示m维的被测物理量，y∈Rm；x表示传感器n维的输出信号，x∈Rn；p表示l维干扰量，p∈Rl。将传感器的输出信号x和干扰量p作为神经网络的输入，传感器的被测物理量y作为神经网络的输出，则f(·)即为非线性补偿函数模型。

在降落伞动态试验或真实应用场景中，伞衣应力可描述为传感器输出电压及对其有影响的其它指标（空气密度、环境温度、湿度、风速、大气压强和海拔高度）之间非线性的映射关系[16-17]。因此，将伞衣径向单位应力σ作为神经网络的输出y( y∈R1)，

式中 F为伞衣单元径向载荷；w为伞衣单元体宽度；t为伞衣单元厚度。

应力传感器输出电压x0构成1维输入变量x( x∈R1)，空气密度x1，环境温度x2，湿度x3，风速x4，大气压强x5，海拔高度x6构成神经网络的6维干扰输入变量p( p∈R6)。其中，伞衣径向单位应力是引起应力传感器输出电压变化的主要因素，x1，x2，x3，x4，x5，x6则作为传感器输出电压变化的次要因素，也需要引入伞衣力学模型。

2 神经网络杂交模型

神经网络杂交模型（neural network hybrid model，NNHM）是结合先验知识建模与神经网络的一种建模方法，可以有效减小网络规模，缩短建模周期，显著地提高建模精度以及模型推广泛化能力。首先，根据系统先验知识，采用传统的非线性回归方法建立一个知识基模型。尽管可能存在着误差，但它描述了系统的主要（主体）特性，并且模型参数具有明确的意义；其次，对于系统中不确定、未建模的非线性特性部分，可以采用一些非参数化的建模方法，例如神经网络方法来进行表征。最后，通过训练得到的神经网络模型可以与知识基模型结合成一个神经网络杂交模型，它能够较好地描述复杂非线性系统的全部动力学特性。

2.1 建模方法

在神经网络杂交模型中，将被测物理量（x0，x1，x2，x3，x4，x5，x6）作为函数的输入，将伞衣径向单位应力σ作为函数的输出，输入输出之间非线性函数关系可以表示为

式中 f1(x0)为知识基假设模型，描述伞衣径向方向单位应力与应力传感器输出电压之间非线性函数关系的主要特性；f2(x0, x1, x2,x3, x4,x5, x6)表示知识基假设模型与实际模型之间的误差，描述伞衣径向方向上的单位应力与应力传感器输出电压，及其它6个指标之间非线性函数关系的局部特性。f1(x0)和f2(x0, x1, x2,x3, x4,x5, x6)共同组成神经网络杂交模型，如图1所示。图中，向量Y=(y1, y2,y3,···,yp)T为KLT(Karhunen-Loevetransform)变换的输出结果。

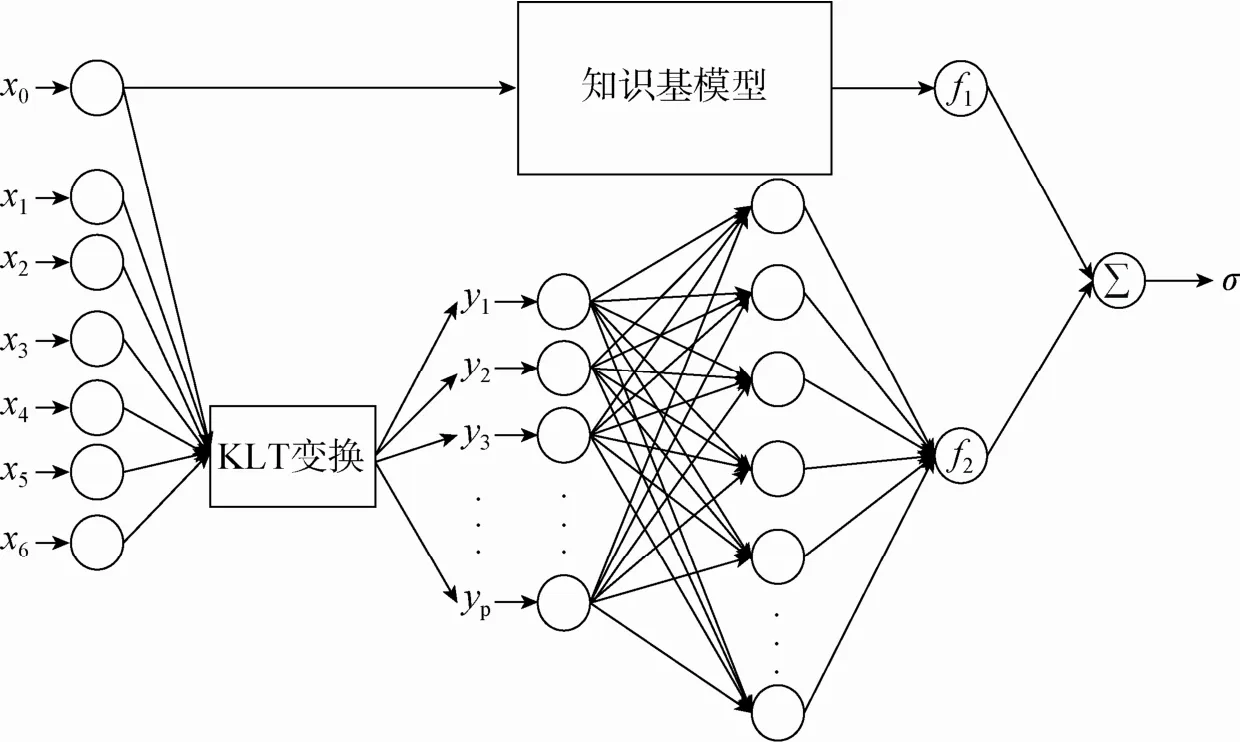
图1 神经网络杂交模型结构Fig.1 Structure of the hybrid neural network model

2.2 知识基模型

CFD-MSD仿真计算将降落伞离散成一系列由弹性力、阻尼力耦合的质点，在外流场作用下，质点受力发生运动。仿真计算将伞衣设定为刚性体，遵循虎克定律，但作为大变形柔性体，在复杂流程作用下伞衣的大变形表现为几何非线性，其力学模型呈现位移的多阶特性，采用线性方程描述模型弹性力会产生较大误差[18]。因此，在应力测量过程中采用应力传感器，将伞衣径向应变转换为电压输出，通过试验方法修正仿真计算误差。根据应力传感器的工作特性，应力传感器在低幅值测量区域具有明显的非线性特性，高幅值测量区域则呈现非线性饱和特性，为揭示伞衣力学模型的本质力学特征，建立三阶多项式方程

式中 w0，w1，w2，w3均为待确定的权值参数向量W1=(w0, w1, w2, w3)T的分量，需要通过非线性拟合方法求解。

2.3 KLT变换

在f2(x0, x1, x2,x3, x4,x5, x6)中，x1，x2，x3，x4，x5，x6作为应力试验的测量干扰因子，在样本数据集上表现为信噪比不高，维度间相关度大。因此，采用基于KLT变换的PCA（principal component analysis）方法对样本数据进行降维处理[19]。

1）应力传感器输出电压及其它6个相关指标数据构成7维向量X

3）采用奇异值分解定理（singular value decomposition，SVD），求解ATA的特征值λi，i=1，2，3，···，m和正交归一化特征向量Vi，i=1，2，3，···，m。

4）按照]1[m,i,λi∈递减（从大到小）的顺序将特征向量]1[m,i,Vi∈重新排列，然后根据能量比，（式中threshold为预先设定阀值）；选择前() p pm＜个最大特征值及其对应的特征向量。

6）由KLT变换得到降维后的向量Y，KLT变换在尽量保留原始向量X的特征信息的前提下，减小特征维度，最大化方差，降低了对向量Y后续处理的计算复杂度。

由式（4）作逆变换，可得

将式（5）带入f2(x0，x1，x2，x3，x4，x5，x6)中，可得

由式（3）、（6）可得

构建一个结构为P×3×1的BP前馈网络，如图1所示。输入层含P个输入节点（即输入层有P个神经元），对应式中KLT变换的向量Y的各个分量；网络输出层含有1个输出节点（即输出层只有1个神经元），对应样本数据中单位应力值σ减去对应的知识基模型的输出，即神经网络包含一个隐层，以一组逐次增高的幂函数作为隐层神经元的激励函数，隐层神经元个数为n，隐层神经元与输出层神经元之间的权重记为W2=(w4, w5, w6,...,wn+3)T。该杂交神经网络模型的输入与输出关系可以描述成式（8）。

式中 hW:Rn×1→R1×1为激励函数，即逐次增高的幂函数。

2.4 训练杂交模型

为了使神经网络杂交模型能够逼近所要表示的非线性映射关系，需要对杂交模型进行训练。基于样本数据（样本数为m），采用拟牛顿法中的BFGS（Broyden-Fletcher-Goldfarb-Shanno）算法训练知识基假设模型[20]，调节权值向量W1，使代价函数J1(W1)最小，即mWinJ1(W1)⇒W1，从而求出知识基模型的权值向量W1。

式中 λ1表示权重衰减参数。

基于训练集的样本数据，采用LM（Levenberg-Marquardt）迭代算法训练BP神经网络[21]，通过迭代方式调节BP神经网络的权值向量W2，使代价函数J2(W2)满足误差精度，从而求出知识基模型的权值向量W2。

式中 λ2表示权重衰减参数；Z(i)表示大变形柔性体径向单位应力σ(i)与知识基函数之差，即

2.5 动态应力补偿

采集跌落试验、风洞试验等动态试验场景中动态样本数据，将应力传感器输出电压作为完成训练的知识基假设模型的输入；将应力传感器输出电压及其它6个相关指标作为KLT变换的输入，其输出向量作为完成训练的BP神经网络的输入，将知识基假设模型的输出与BP神经网络的输出之和作为神经网络杂交模型的输出，即动态应力补偿结果。

3 静态试验

为了验证上述方法的有效性，在伞衣表面沿径向方向安装应力传感器（曲梁直径∈[5,1 0]mm、宽度∈[5,1 0]mm 、厚度∈[0.2, 0.5]mm，尼龙介质宽度b∈[5,1 0]mm、厚度∈[0.05, 0.2]mm ，工作电压Uin=3V，放大器增益250）。应力传感器共3种规格，对应50kg、100kg、150kg载荷，具体规格尺寸如表1所示。尼龙介质采用544高强度锦丝绸材质，厚度为0.9mm。应力传感器使用TML的FLA-5-11应变片，适用温度范围–20℃~80℃。

表1 应力传感器曲梁规格Tab.1 Stress sensor specification data

静态标定试验在人工气候实验室进行，通过调节环境温度、湿度、气压和气体成分等环境参数，来模拟动态试验场景的环境条件。由高精度万能材料试验机输出大小不等的拉力载荷F，沿伞衣介质的径向方向作用于伞衣两端。伞衣径向应力计算公式为σ=F( w× t)，式中w取6.5mm，t取0.9mm。

应力传感器输出电压均随着环境温度的升高而上升，这是因为随着温度升高，伞衣材料的弹性模量反之下降。例如在伞衣径向应力为0.5MPa时，伞衣径向形变加大。在温度较低环境中（–20℃~50℃），弹性模量下降超过80%；在温度较高环境中（50℃~80℃），弹性模量下降不超过20%。这表明环境温度也是影响伞衣力学模型的因素之一，且两者之间呈现非线性关系。试验结果表明，应力传感器输出与环境温度的对应关系近似相同，与伞衣载荷大小无关。此外，应力传感器输出与湿度的之间也存在相似变化。

如图2所示，应力传感器输出电压随着伞衣径向应力的增加而增加，应力传感器输出电压与伞衣径向应变除了在单调性上保持一致之外，还出现应力屈服点，两者之间呈现为复杂非线性增函数关系，即知识基模型f1( x0)。此外，从图上可以看出，在高精度万能材料试验机输出载荷恒定，即伞衣径向应力不变的条件下，增加风速，应力传感器输出电压随之增加，即风速是影响伞衣力学模型的因素之一，本文采用f2(x0, x1, x2,x3, x4,x5, x6)描述这种不确定因素对伞衣力学模型的影响。

图2 温度25℃时不同风速下应力-电压曲线Fig.2 Average stress vs. sensor signal for different air speeds; temperature=25℃

4 试验结果与分析

采用静态样本数据训练知识基模型，设置训练最大迭代次数为500，学习率为0.02，收敛精度为0.5。经过109轮迭代后收敛，J1(W1)＜0.5，即代价函数满足收敛精度。知识基模型的权值向量估计值为W1=（0.04805， 1.49642，-1.76484，1.0 968 9）。

采用静态样本数据训练BP神经网络模型，设定训练最大迭代次数为1 000，学习率为0.02，收敛精度为0.1。通过分析训练结果可知，隐层神经元节点数为7时，训练结果最好，此时模型经过69轮迭代后收敛，J2(W2)=0.06933，即代价函数满足收敛精度。神经网络模型权值向量估计值W2=（0.65679， 2.99143， 1.01206， 0.94953, 1.05043，-1.64913， 1.44707）。

选取2013年10月份基于小型平面圆形伞进行的4次风洞试验数据作补偿试验验证，将样本值依次输入神经网络，由神经网络杂交模型进行非线性补偿，补偿结果符合小型平面圆形伞的充气规律。如图3(a)所示，在环境温度为25℃，风速为20m/s条件下，开伞峰值在0.1s之内出现，伞衣表面所受应力达到最大，随后伞衣在气弹力作用下逐渐回弹，随后迅速出现有规律的呼吸现象，呼吸频率及幅值逐渐降低，这符合小型平面圆形伞的结构特性。图3(b)、图3(c)、图3(d)分别表示在环境温度为25℃，风速为30m/s，40m/s，50m/s条件下的大变形柔性体工作过程的应力变化曲线。从这3种工况下伞衣应力变化过程可以看出，随着来流速度的增大，开伞动载峰值和稳定时的伞衣应力逐渐增大，开伞峰值出现时刻逐渐提前。

图3 温度25℃时应力补偿曲线Fig.3 Compensation strain vs. time; temperature=25℃

将4种风速的伞衣应力峰值的仿真结果和补偿结果作比较，由表2可知，仿真预测的伞衣应力峰值比补偿应力峰值稍大，但偏差在5%以内，最小偏差仅为1.6%，因此可认为经应力补偿模型修正后，伞衣应力补偿精度基本满足工程任务设计需求。

表2 温度25℃时开伞峰值验证Tab.2 Validation of peek value of parachute opening force; temperature=25℃

为了比较不同类型神经网络算法的训练速度及收敛精度，将杂交神经网络与标准BP神经网络（梯度下降）、改进BP神经网络（LM）及RBF（radial basis function）算法进行对比。试验环境为：Intel Core i5-4570（3.6GHz），8.0Gbyte RAM，Windows 8.1（32bit），MATLAB R2014a。试验中，样本数为450，学习率为0.02，最大迭代次数为1 000轮，目标误差精度为0.1；参数方面，RBF的径向基函数分布为1.1。结果如表3所示，在这4种算法中，虽然RBF神经网络的收敛速度最快，但杂交神经网络收敛速度仅次于RBF神经网络，且收敛精度最高，对动态应力的补偿效果最好。

表3 神经网络杂交模型与其它神经网络模型补偿结果对照Tab.3 Compensation result comparison between NNHM and other neural network model

5 结束语

本文首次采用神经网络方法对降落伞动态伞衣应力进行补偿，主要结论如下：

1）本文讨论了神经网络杂交模型在降落伞开伞过程中对动态应力非线性补偿的应用。补偿结果符合小型平面圆形伞的充气规律，系统综合处理精度小于3%，说明本文提出的补偿方法可以有效应用于伞衣动态应力的补偿计算；仿真结果和补偿结果的数据偏差率小于5%，说明该补偿方法可为流固耦合计算提供仿真分析、评估、验证与自动化测试技术支持。

2）神经网络杂交模型的训练存在泛化问题，本文充分考虑试验环境中的海拔高度、风速、温度以及其它传感器参数所产生的干扰因素，在均方误差最小的情况下，通过寻找最优线性映射投影，有效去除数据冗余，突出样本特征，提高神经网络杂交模型的训练速率、补偿精度及泛化能力。

3）传感器非线性补偿是一个神经网络杂交模型的逼近问题，与传统神经网络补偿方法相比，神经网络杂交建模方法利用知识基假设模型的引导特性，使用先验知识拟合模型的主要特征，能够有效补偿应力传感器输入输出映射关系的非线性误差，显著提高有效减小网络规模，缩短建模周期。

References)

[1] STEIN K R，BENNEY R J，Steeves E C. A Computational Model That Couples Aerodynamic and Structural Dynamic Behavior of Parachutes During the Opening Process[R]. NASA-ADA 264115, 1993.

[2] STEIN K R，BENNEY R J. Parachute Inflation: AProblem in Aero Elasticity[R]. NASA-ADA 284375, 1994.

[3] KALRO V，TEZDUYAR T E. A Parallel 3D Computational Method for Fluid–structure Interactions in Parachute Systems[J].Computer Methods in Applied Mechanics and Engineering, 2000, 190(3): 321-332.

[4] SATHE S, BENNEY R, CHARLES R, TEZDUYAR T E. Fluid–structure Interaction Modeling of Complex Parachute Designs with the Space–time Finite Element Techniques[J]. Computers & Fluids, 2007, 36(1): 127-135.

[5] TAKIZAWA K, TEZDUYAR T E. Computational Methods for Parachute Fluid–structure Interactions[J]. Archives of Computational Methods in Engineering, 2012, 19(1): 125-169.

[6] TAKIZAWA K, SPIELMAN T, MOORMAN C, et al. Fluid-structure Interaction Modeling of Spacecraft Parachutes for Simulation-based Design[J]. Journal of Applied Mechanics, 2012, 79: 1-9.

[7] TAKIZAWA K, TEZDUYAR T E, BOBEN J, et al. Fluid–structure Interaction Modeling of Clusters of Spacecraft Parachutes with Modified Geometric Porosity[J]. Computational Mechanics, 2013, 52(6): 1351-1364.

[8] TUTT B. FLUID Structure Interaction Parachute Benchmark Models in LS-DYNA[C]. AIAA Aerodynamic Decelerator Systems (ADS) Conference, Daytona Beach, Florida, 2013.

[9] 程涵, 余莉, 李胜全. 基于ALE的降落伞充气过程数值仿真[J]. 南京航空航天大学学报, 2012, (3): 290-293.

CHENG Han, YU Li, LI Shengquan. Numerical Simulation of Parachute Inflation Process Based on ALE [J]. Journal of NanjingUniversity of Aeronautics & Astronautics, 2012, 44(3):290-293. (in Chinese)

[10] YU L, CHENG H, ZHAN Y N, et al. Study of Parachute Inflation Process Using Fluid–structure Interaction Method[J]. Chinese Journal of Aeronautics, 2014, 27(2): 272-279.

[11] 连亮, 王中阳, 张红英, 等. 基于ALE方法的群伞稳降阶段的数值模拟[J]. 航天返回与遥感, 2014, 35(1): 21-28.

LIAN Liang, WANG Zhongyang, ZHANG Hongying, et al. Numerical Simulation of Cluster Parachute System During Steady-state Descent Phase Based on ALE Method[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 21-28. (in Chinese)

[12] TAIB M N, NARAYANASWAMY R. Multichannel Calibration Technique for Optical-fibre Chemical Sensor Using Artificial Neural Network[J]. Sensors and Actuators B: Chemical, 1997, 39: 365-370.

[13] DEMPSEY G L, ALIG J S, ALT N L, et al. Control Sensor Linearization Using Artificial Neural Networks[J]. Analog Integrated Circuits and Signal Processing, 1997, 13(3): 321-332.

[14] ARPAIA P, DAPONTE P, GRIMALDI D, et al. ANN-based Error Reduction for Experimentally Modeled Sensors[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(1): 29-30.

[15] TIAN Sheping, DING Guoqing, YAN Detian, et al. Nonlinear Dynamic Modelling of Sensors Based on Recursive Neural Network[J]. Journal of Test and Measurement Technology, 2004, 18(2): 99-103.

[16] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997:170-273.

WANG Lirong. Theory and Application of Parachute[M]. Beijing: Astronautics Press, 1997: 170-273. (in Chinese)

[17] 龚文轩. 降落伞开伞高度对开伞动载影响分析[J]. 南京航空航天大学学报, 1996, 28(03): 39-45.

GONG Wenxuan. Parachute Added Mass and Opening Forces[J]. Acta Aeronautica Et Astronautica Sinica, 1995, 16(1): 39-45. (in Chinese)

[18] 余莉, 史献林, 明晓. 降落伞充气过程的数值模拟[J]. 航空学报, 2007, 28(01): 52-57.

YU Li, SHI Xianlin, MING Xiao. Numerical Simulation of Parachute During Opening Process[J]. Acta Aeronautica Et Astronautica Sinica, 2007, 28(1): 52-57(in Chinese).

[19] Abhilash Alexander Miranda, Yann-Aël Borgne, Gianluca Bontempi. New Routes from Minimal Approximation Error to Principal Components[J]. Neural Processing Letters, 2008, 27(3): 197-207.

[20] HAELTERMAN R. Analytical Study of the Least Squares Quasi-newton Method for Interaction Problems[D]. Ghent, Belgium: Ghent University, 2009.

[21] JIN Q. On A Regularized Levenberg–Marquardt Method for Solving Nonlinear Inverse Problems[J]. Numerische Mathematik, 2010, 115(2): 229-259.

Research of Dynamic Stress-compensation Method for Parachute Based on Neural Network Hybrid Model

LUO Tao ZHUANG Yi
（College of Computer Science and Technology, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China）

According to the computation model of the canopy inflation of the parachute which couples Computational Fluid Dynamics to Mass Spring Damper, a neural network hybrid modeling approach is proposed and applied to sensor compensation. The static data samples are adopted in the calculation of the compensation to real-time data samples which are from tunnel test or fall–down test. The numerical values are correlated well with the results of simulation calculation. It indicates that the stress-compensation method accurately reflects the transient stress change of parachute, and validates the convergence and veracity. The neural network hybrid modeling is superior to general neural network modeling because the former possesses the characteristics of small network scale, higher convergence speed, higher calibration precision and better generalization performance.

stress-compensation; neural network; hybrid modeling; parachute

V448.15

A

1009-8518(2015)05-0020-09

10.3969/j.issn.1009-8518.2015.05.003

罗韬，男，1979年生，2005年获南京航空航天大学计算机应用专业硕士学位，现在南京航空航天大学计算机应用专业攻读博士学位。研究方向为分布式计算、机器学习。E-mail：focse@163.com。

2015-03-20