某型超声速半流伞气动热及气动特性研究

李旭东 周伊鹏 张红英 童明波

（1 南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016）

（2 北京空间机电研究所，北京 100094）

0 引言

随着航天事业任务需求的多样性，新一代多用途飞船成为各国研究的重点，如美国的“猎户座”、“龙飞船”[1]。我国多用途试验飞船的研究也在如火如荼地进行中[2]，在多用途飞船返回（再入）过程中，返回舱将以自旋方式半弹道再入返回大气层，按照返回舱的气动计算结果，返回舱再入飞行过程中，在超声速段返回舱可能存在第二个配平点，有可能出现姿态翻滚的情况，于是就在总体设计中配备了一个稳定伞，来保证返回舱姿态。该伞伞形为半流伞，打开高度为26km，打开时伞船系统Ma=3.0。当高速空气流过伞衣表面时，由于气体粘性的阻滞作用，物面边界层内具有很大速度梯度，各气流层间产生了强烈的摩擦，其结果使气流的动能不可逆地转变为热能，造成伞衣表面附近温度的升高，气动热问题成为该降落伞气动和结构设计必须考虑的一个问题[3-5]。

国内外针对超声速半流伞的研究主要是通过风洞试验的方式，相关的仿真分析还处于空白状态，本文在借鉴传统飞行器仿真分析方法的基础上，创新性的开展了超音速半流伞的气动热及气动特性分析。

本文首先对此型超声速半流伞进行了合理的简化，并且验证了简化模型的合理性和可靠性，之后在多种工况下对二维半流伞模型进行仿真分析，得到了此型半流伞的流场分布情况和温度分布情况。

1 湍流模型

由于降落伞有很多的开孔且壁面很薄，网格量很大，考虑到提高计算效率，本文在计算中选取 B-L湍流模型，B-L模型为典型的零方程模型。该模型是由Baldwin和Lomax在1978年提出的[6-8]，主要研究物面边界层流动，它的涡粘性tμ对外部和边界层内部采用不同方法估算：

式中 y为距离壁面的法向距离；yc表示附面层厚度。

边界层内部涡粘性估算有以下公式：

式中 ρ为边界层内部流体密度；l为长度尺度（由式（3）表示）；为涡量。

长度尺度l用普朗特混合长度模型与Van Driest衰减函数来估计：

式中 k为普朗特常数，其值默认为0.4；y+为近壁面网格无量纲距离；A+为阻尼长度，取值为常数26。涡量方程：

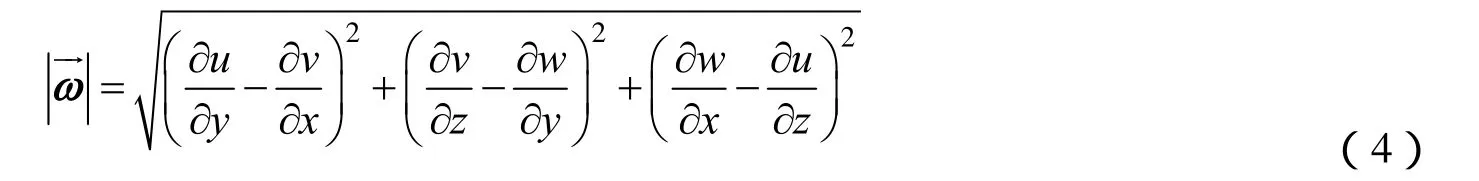
式中 u、v、w为速度向量三个方向的分量。附面层外部涡粘性方程如下：

式中 Fw、 FK（y）为中间变量，分别由式（6）、（7）表示。

式中 smax为边界层内湍流速度最大值；ymax为速度尺度最大值处的y值。

式中 Udif为边界层内速度最大值和最小值之间的差值。

2 仿真模型简化及验证

2.1 仿真模型及简化

超声速半流伞的外形如图1所示，半流伞伞衣结构形状呈210°球面，在超声速条件张满后状态下，伞衣的形状趋于半球形。该伞总共有18条水平伞带，水平伞带宽30mm，在半流伞工作中主要起减速稳定的作用；而加强带的主要功能是连接18条水平伞带以及加强伞衣结构性能[9]。

图1 半流伞外形Fig.1 Configuration of half-flow parachute

超声速伞的结构透气性（27%）远大于伞衣材料的透气性（小于5%），所以在CFD计算过程中可以假设伞衣材料不透气。与此同时，虽然降落伞属于柔性体，但此类型降落伞在超声速阶段工作，设计的结构透气性大，伞衣结构的弹性模量小，所以可以认为伞衣在超声速阶段的不同速度下的外形变形很小，因此在CFD计算工况中都采用理想设计外形并合理假设伞体为外形不变的刚体。伞绳的直径远小于伞模型尺寸，在所有CFD仿真过程中可以忽略伞绳的影响[10]。

由于伞体实际外形的孔和面都很多，可以达到几百个，每个孔在CFD结构网格划分中都需要生成一个BLOCK，几百个BLOCK在CFD超声速流计算中是不可以承受的，而本文关注的是伞附近流场的温度、速度以及伞衣表面温度分布，不是伞的结构特征，所以本节对半流伞仿真模型进行合理地简化，忽略半流伞的结构加强带，只考虑起主要稳定减速作用的水平伞带，如图2所示[11-12]。

图2 半流伞简化模型Fig.2 Simplified model of half-flow parachute

2.2 网格生成

为了提高仿真效率，带加强带的半流伞网格采用四分之一模型，网格生成数为1.6×106，如图3（a）所示；去除加强带的简化模型采用二分之一模型，网格生成数为 2.8×106，如图 3（b）所示。由于来流是超声速的，扰动不上传，所以伞底边流场边界可以设得较靠近伞底面，以此减少网格数量。对于考虑物面附近粘性效应同时为了满足湍流计算精度要求，壁面网格精度保证将y+值调至接近1[13]。

图3 半流伞的流场网格Fig.3 Flow-field mesh of half-flow parachute

2.3 参数和边界条件

由于是超声速流动，空气必然会发生压缩，因此该类问题视为可压缩流动问题。为了比较加强带对流场的影响，选取Ma=3.3，高度15km的计算工况，分别对考虑加强带的模型和简化的模型基于N-S方程进行模拟仿真计算。

远场边界为无反射边界条件，壁面均设为粘性的无滑移条件，物面边界设为绝热壁壁面处理。对于绝热壁面，其热流密度qw=0[14]。

2.4 模型验证

图4（a）为简化模型的半流伞伞面绝热温度云图，伞面的绝热温度范围在544.2~753.2K，图4（b）为有加强带的半流伞伞面绝热温度云图，伞面绝热温度范围在538.7~760.8K，从伞面的绝热温度在和最低绝热温度来看，温度相差较小（在10K以内）。两者的最高绝热温度都处于第一条伞带的内表面上，分别为753.2K与760.8K。伞带上温度趋势也较为一致，同时加强带伞面云图显示为“绿色”，所以加强带不是气动热严重的区域。

图5（a）为简化模型的流场压力分布云图，最高动压值为196.7kPa。图5（b）为有加强带的半流伞流场压力分布云图，最高压力值为195.8kPa。可以看出流场压力分布较为一致，激波位置以及高压区低压区的分布差别很小，压力数值范围也几乎一样。

因此可以得到加强带对流场分布以及气动热的计算结果影响较小的结论，简化的半流伞模型是比较合理的。

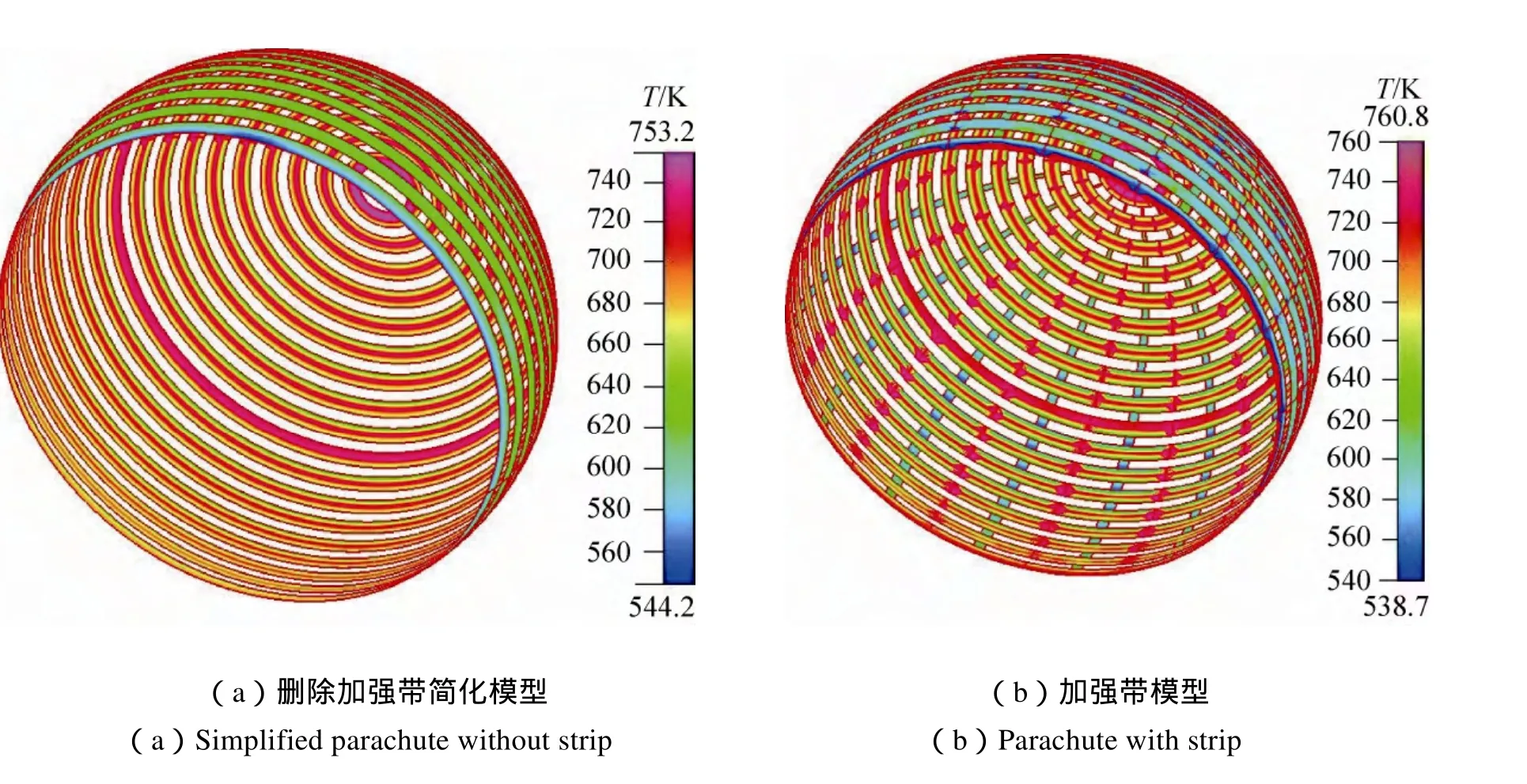
图4 伞面绝热温度云图Fig.4 Adiabatic temperature of parachute

图5 流场压力云图Fig.5 Flow-field pressure of parachute

3 半流伞流场特性研究

基于加强带对半流伞的流畅影响较小，同时半流伞伞体模型为轴对称模型，因此本节采用二维轴对称模型进行仿真，计算网格如图6所示。

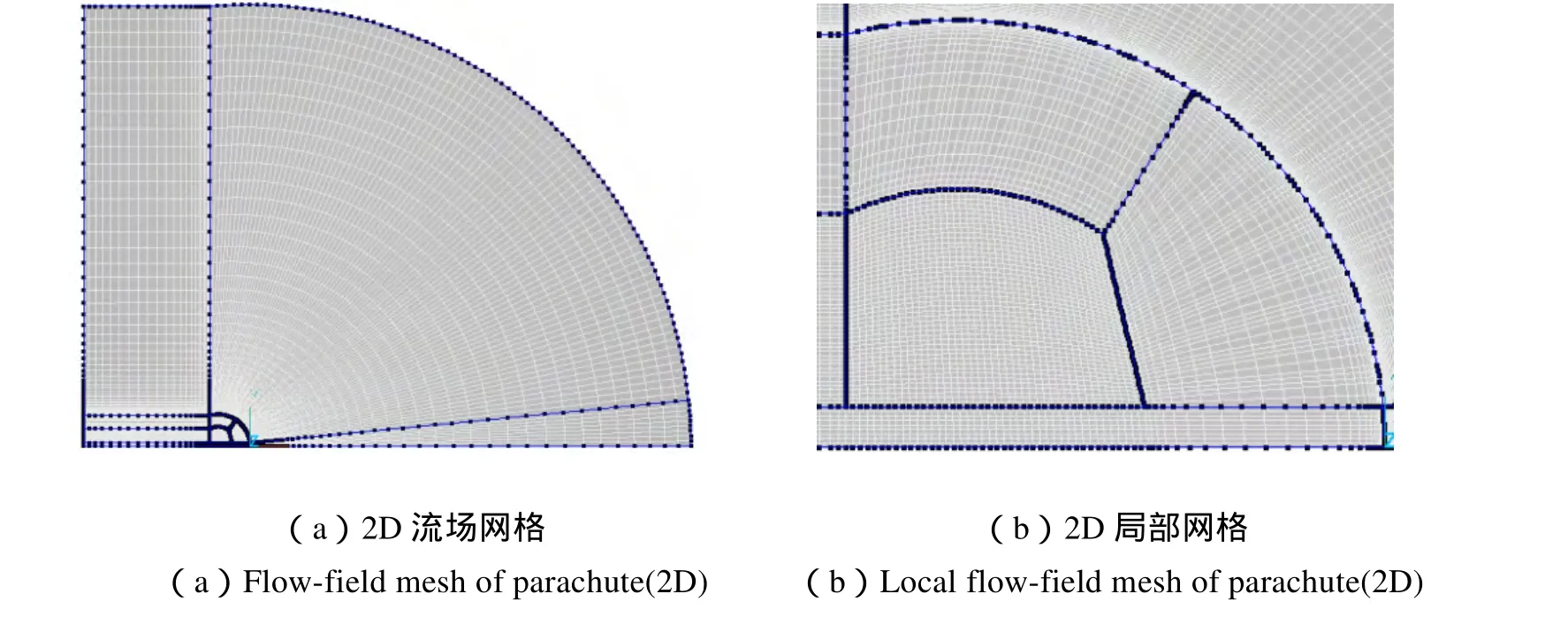
图6 二维半流伞网格Fig.6 Flow-field mesh of half-flow parachute(2D)

3.1 计算工况及边界条件

超声速半流伞静态仿真工况如下表1所示：

表1 不带前体的静态工况Tab.1 Static condition without spacecraft

把伞面物面设为辐射壁面边界条件，表现为：

式中 λ为热传导系数；Tc为附面层温度；Tw为壁面温度；δ为单元中心到壁面表面的投影距离；ε为伞衣表面发射率；σ为斯忒藩-波尔兹曼常数[15]。

伞衣材料为辐射芳纶，伞面发射率 ε=0.8，式（9）确定了壁面温度和热通量的耦合，辐射热流。等流场稳定后，伞面、伞内温度不再变化，流场也不再变化，净热流为零，可以推导热平衡后的状态，即对伞衣输入的热流，也就是气动力加热流qw等于伞衣对外部空间的辐射流。

3.2 流场分析

图7~8为四个不同工况下的流场的速度云图和压力云图，图中H为高度。明显看出，伞内积攒了大量的空气，形成了高压区，而且每个孔都有空气流出，尤其在伞顶孔区域，流速极快，形成了低压区，也可以看出该伞由于具有较大的结构透气性（为了使流入该伞的空气尽可能多地排出去），伞衣底边的激波可以被“吞下”。符合该降落伞的气动特性。相同高度下，随着速度值的增大，流场的动压值也是在增大的；相同马赫数下，随着高度的降低，流场的动压值也在增大。同时需要注意的是伞衣内外表面压强差值较大，在半流伞设计过程中，要充分考虑伞衣的结构安全性问题。

本节二维计算中，伞口激波位置与前一节有些差别，原因是：二维网格和三维网格在分布上不同，导致激波捕捉上存在一定的差异；本节伞面壁面条件为辐射壁面，验证模型使用的是绝热壁，壁面条件本身对CFD计算会有影响。不过整体趋势较为一致，不影响本节的研究分析。

图7 流场速度云图Fig.7 Velocity distribution of flow-fields

图8 流场压力云图Fig.8 Pressure distribution of flow-fields

3.3 气动热分析

图9为四个不同工况下的流场的温度云图，从流场温度可以大致看出超声速半流伞流场的温度分布，伞内热环境由于气流的积攒比较恶劣，伞顶孔上方空气动压大，流速快，因此热量可以由空气带走，使得该区域的流场温度较低，而激波下方的远场温度就是对应高度上的静温。

Ma=2.0，H=15km时，流场最高温度是439K；Ma=2.5，H=15km时，流场的最高温度是549.4K，Ma=3.3，H=15km时，流场最高温度是770.9K；Ma=3.3，H=25km时，流场最高温度是783.1K。

图9 流场温度云图Fig.9 Temperature distribution of flow-fields

对比同一高度下，马赫数越大，流场温度越高，热环境越恶劣。同一马赫数，比较高度15km与25km，流场最高温度差别不是很大。对此分析，虽然马赫数相同，但是高度25km工况下的速度、静温、动力粘性系数均大于高度15km的工况下，而高度15km大气环境压力大于高度25km下大气环境压力，两者相互干扰，导致两种工况下的最高温度相差不是很大，因此不能有对比性的结论。

图9中四个工况伞衣内表面温度始终是要高于外表面温度。且伞面温度最高（如表2）的区域都处于伞顶口附近的伞带（第一条伞带）内表面上。分析原因：伞顶口处空气接近垂直地打到伞顶口最近的伞带内表面上，流速形成停滞或者接近停滞，动能很大程度地转化为了热能，并且热量也不容易被带走，所以此处的气动加热最为严重。

表2 伞面最高温度Tab.2 Highest temperature of parachute

同时第十八条伞带（靠近伞裙的伞带）由于顺着来流，气动摩擦很严重，理论上此处的气动加热会严重，但是此处的热量可以被流动的空气带至伞带后方，在流场温度云图上也能很清晰辨别，伞裙外侧会显示有像“红色镰刀”状的区域，因此此处的伞带温度并不是真实气动加热最严重的区域。

4 结束语

本文主要研究了某型超声速半流伞的气动特性和气动热特性，首先对模型进行合理的简化，并且验证了简化模型的可靠性，之后对二维模型的流场特性进行了分析，相关结论如下：

1）加强带对流场分布以及气动热的计算结果影响较小，在实际仿真时可以忽略。

2）相同高度下，随着速度值的增大，流场的动压值也是在增大的；相同马赫数下，随着高度的降低，流场的动压值也在增大。

伞衣内表面温度始终是要高于外表面温度，且伞面温度最高的区域都处于伞顶口附近的伞带（第一条伞带）内表面上。

References)

[1] 高滨. 国外载人航天器回收着陆技术的进展[J]. 航天返回与遥感, 2009, 30(2): 1-9. GAO Bin. An Overview of Recovery and Landing Systems for Foreign Manned Spacecrafts[J]. Spacecraft Recovery & Remote Sensing, 2009, 30(2): 1-9. (in Chinese)

[2] 杨雷, 张柏楠, 郭斌. 新一代多用途飞船概念研究[J]. 航空学报, 2015, 36(3): 703-713. YANG Lei, ZHANG Bonan, GUO Bin. Concept Definition of New-generation Multi-purpose Manned Spacecraft[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 703-713. (in Chinese)

[3] 韩晋阳, 徐宏, 高峰. 超声速半流伞设计与分析[J]. 航天返回与遥感, 2013, 34(5): 20-28. HAN Jinyang, XU Hong, GAO Feng. Design and Analysis of Supersonic Half-flow Parachute[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(5): 20-28. (in Chinese)

[4] 张红英, 童明波, 吴剑萍. 降落伞充气理论的发展[J]. 航天返回与遥感, 2005, 26(3): 16-21. ZHANG Hongying, TONG Mingbo, WU Jianping. The Development of Parachute Inflation Theories[J]. Spacecraft Recovery& Remote Sensing, 2005, 26(3): 16-21. (in Chinese)

[5] 程涵, 余莉, 李少腾, 等. 折叠降落伞展开过程研究[J]. 航天返回与遥感, 2012, 33(2): 1-6. CHENG Han, YU Li, LI Shaoteng, et al. A Study on the Opening Process of Folded Parachute[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(2): 1-6. (in Chinese)

[6] 肖志祥, 李凤蔚. 三种湍流模型模拟能力的对比[J]. 西北工业大学学报, 2002, 20(3): 351-355. XIAO Zhixiang, Li Fengwei. Comparison of Predictive Capabilities of Three Turbulent Models[J]. Journal of North Western Polytechnical University, 2002, 20(3): 351-355. (in Chinese)

[7] Stein K R, Benney R, Kalro V, et al. Parachute Fluid-structure Interactions: 3-D Computation[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190: 373-386.

[8] 董素君, 居世超, 齐玢, 等. CFD_FASTRAN气动热计算模型及网格效应分析[J]. 航空计算技术, 2011, 41(2): 40-42. DONG Sujun, JU Shichao, QI Bin, et al. Model and Grid Dependency of Hypersonic Aerodynamic Heating Calculation Accuracy by CFD-FASTRAN Software[J]. Aeronautical Computing Technique, 2011, 41(2): 40-42. (in Chinese)

[9] 连亮, 张红英, 李方, 等. 结构参数对火星探测用伞开伞性能的影响[J]. 航天返回与遥感, 2012, 33(6): 24-29. LIAN Liang, ZHANG Hongying, LI Fang, et al. Influence of Structure Parameters on Inflation Performance of Parachute Used for Mars Exploration[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(6): 24-29. (in Chinese)

[10] Takizawa K, Wright S, Moorman C. Fluid-structure Interaction Modeling of Parachute Clusters[J]. International Journal for Numerical Methods in Fluids, 2011(65): 286-307.

[11] Edward J F. System Design Overview of the Mars Pathfinder Parachute Decelerator Subsystem [R]. AIAA -97-1511, San Francisco: 14th Aerodynamic Decelerator Systems Technology Conference, 1997.

[12] 荣伟, 陈旭. 火星探测用降落伞研制试验简介[J]. 航天返回与遥感, 2007, 28(1): 12-17. RONG Wei, CHEN Xu. Resume of the Tests about Parachute Development for Mars Exploration Mission [J]. Spacecraft Recovery & Remote Sensing, 2007, 28(1): 12-17. (in Chinese)

[13] 李真, 董玉立, 冯成良, 等. 基于CFD- FASTRAN的导弹折叠弹翼展开过程模拟[J]. 弹箭与制导学报, 2015, 35(1): 5-8. LI Zhen, DONG Yuli, FENG Chengliang, et al. Simulation of Deployment of Missile Folded Wings Based on CFD-FASTRAN[J]. Journal of Projectiles Rockets Missiles and Guidance, 2015, 35(1): 5-8. (in Chinese)

[14] 王发民, 沈月阳, 姚文秀. 高超音速升力体气动力气动热数值计算[J]. 空气动力学学报, 2001, 19(4): 439-445. WANG Famin, SHEN Yueyang, YAO Wenxiu. Aerodynamic and Aerothermal Numerical Simulation of Hypersonic Lifting Body Configuration[J]. Journal of Aerodynamics, 2001, 19(4): 439-445. (in Chinese)

[15] 王利荣. 降落伞理论及应用[M]. 北京: 宇航出版社, 1997: 116-126. WANG Lirong. Parachute Theory and Application[M]. Beijing: China Astronautics Press, 1997: 116-126. (in Chinese)