着陆器倾斜状态对伽玛关机敏感器测高精度的影响分析

沈超 王晓博 罗伟 吴世通 黄伟

（1 北京空间机电研究所，北京 100094）

（2 北京华航无线电测量研究所，北京 100013）

0 引言

“嫦娥三号”探测器实现了月球着陆，为我国探月工程的采样返回和载人登月奠定了重要基础。由于月球没有大气，月球着陆器在月面着陆过程中无法利用降落伞实现减速，只能利用制动发动机的主动方式实现减速，并采用机械式软着陆缓冲机构实现月面着陆[1]。为实现月球着陆器的着陆稳定性，需通过各种敏感器来辅助实现，如多普勒雷达、雷达高度计、激光高度计、CCD相机等着陆敏感器[2]。俄罗斯研制的“KAKTUS”伽玛高度计是一种低高度敏感器，已成功应用在联盟TM飞船[3]；美国NASA的“自动登陆和危险避免技术”（ALHAT）项目正在研究雷达敏感器和激光高度计方面的新技术，以实现月球着陆器100m ～20km范围内的高度测量[4-8]；此外，美国在进行Apollo航天器着陆技术研究时曾进行触杆式敏感器的测试，航天器降落过程中在触杆触地瞬间发出反推火箭点火信号，该触杆也是一种低高度敏感器[3,9-10]。我国自主研制的伽玛高度控制装置已成功应用于“神舟”号载人飞船，能实现0～20m低高度范围内的精确高度测量，当返回舱降落至离地面1m左右高度时，伽玛高度控制装置能给反推发动机点火指令，从而实现返回舱的缓冲降落。

伽玛关机敏感器的作用也是实现低高度的测量，其工作原理与伽玛高度控制装置相同并已成功应用于“嫦娥三号”探测任务。伽玛关机敏感器安装于着陆器底板，其功能是在着陆器缓速下降至距月面3m左右高度时给出制动发动机关机指令，从而使着陆器以自由落体的方式实现安全着陆。虽然伽玛关机敏感器与伽玛高度控制装置的工作原理相同，但是伽玛高度控制装置的应用环境是地面大气环境，而伽玛关机敏感器的应用环境是月球真空环境，其测高精度受返回舱或着陆器载体的不同和γ源剂量的不同会有很大影响，且伽玛高度控制装置仅针对返回舱1m左右高度的测高精度进行了试验测量，对3m左右高度的测高精度没有试验参考数据。文献[11]中提到当航天器纵轴与地面不垂直时会造成点火高度的偏差，而着陆器在月面下降过程中也不可能始终保持水平姿态，其下降过程中不同的倾斜姿态会对伽玛关机敏感器的测高精度产生不同的影响。为了使着陆器能够安全着陆，尽可能的减小着陆冲击，需要获得伽玛关机敏感器在以着陆器为载体时，着陆器不同倾斜状态对其测高精度的影响程度，本文重点分析3m左右高度的测高精度，从而实现伽玛关机敏感器关机高度的精确测量。

1 测高原理

伽玛关机敏感器是一种通过γ光子计数实现高度判别的低高度敏感器，它一般由发射器和接收处理器组成。伽玛关机敏感器实现测距的物理模型如图1所示。发射器内装γ源，它以辐射角Ψ向月面辐射γ光子；γ光子经月面反射和散射后由接收处理器内前端光电探测器中的NaI晶体接收；光电倍增管将光信号转换成微弱的频率脉冲电信号，并由信号处理电路将频率信号转换成高度信号。一定的高度与一定的计数频率相对应，实现高度判别[12-14]。γ源的辐射角Ψ直接影响接收处理器接收的γ光子数[15]，发射器和接收处理器的水平距离d和垂直距离B也应满足一定的位置关系，从而使伽玛关机敏感器具有较宽的高度测量范围H。

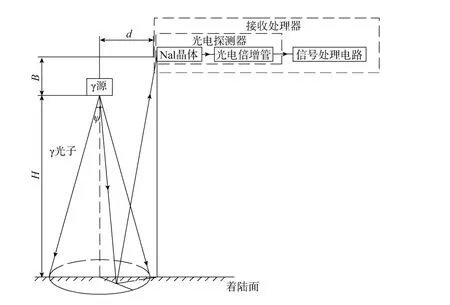
图1 伽玛关机敏感器测距物理模型Fig. 1 The physical model of γ-sensor

伽玛关机敏感器通过水平地面的静态吊高试验获得不同高度的频率计数（即静态特性曲线），利用频率与高度的对应关系实现关机高度的调试。伽玛关机敏感器在着陆器上的几何布局是固定的，其关机指令高度也是在水平姿态下标定的高度，而着陆器下降过程中的姿态可能发生变化，倾斜姿态相对水平姿态就会发生γ射线传输距离、辐射场面积及光电探测器光子接收面积等因素的变化，造成的γ光子计数频率的变化将导致关机高度基准参数的改变，致使接收处理器在倾斜姿态下与水平姿态下的γ光子计数频率不同。从而致使倾斜姿态相对水平姿态时伽玛关机敏感器的关机高度精度产生偏差。

2 试验方案

着陆器下降过程可能发生倾斜，月面着陆区也可能存在一定坡度，而着陆器月面下降过程通过姿态控制能保证其轴线与月面垂线夹角小于4°，月面着陆区的选择能保证其月面坡度小于8°，但是伽玛关机敏感器是在水平地面进行其计数频率的标定，因此可以认为着陆器在下降过程中其轴线与月面垂线的夹角不大于 12°。为确定着陆器倾斜状态对伽玛关机敏感器测高精度的影响，将伽玛关机敏感器安装于着陆模拟器上进行着陆器不同倾斜角度时的精度验证试验，获得伽玛关机敏感器在着陆器不同倾斜角度时的静态特性数据，确定着陆器倾斜状态引起γ光子计数频率的变化规律以及对测高精度的影响程度。

伽玛关机敏感器在着陆模拟器上的安装布局如图2所示。

为了获得各个方向不同倾斜角度时的静态特性数据，使着陆模拟器分别进行水平状态和绕Y、Z轴分别倾斜±4°、±8°和±12°共13个状态的精度验证试验，并定义着陆模拟器绕+Y、+Z轴沿X轴正向倾斜为正角度倾斜，沿X轴负向倾斜为负角度倾斜，每个状态由低到高在1.1～10m内共进行21个高度点静止状态下的计数频率测量，通过不同倾斜状态与水平状态时的关机高度比较分析倾斜状态引起的关机高度精度误差。

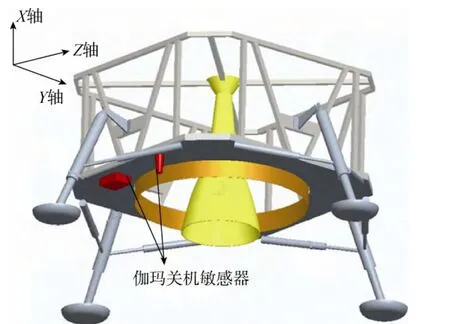
图2 伽玛关机敏感器安装布局Fig. 2 The layout of γ-sensor

3 试验结果分析

试验获得着陆模拟器绕Y、Z轴倾斜±4°、±8°和±12°时的静态特性曲线比较如图3～5所示，从整体数据可以发现不同倾斜角度时的计数频率与水平状态时差异不大。

由不同倾斜角度时的静态特性曲线可以看出，高度较高时，倾斜角度对计数率的影响较小，在 5m以下高度时倾斜角度对计数率有一定影响。由于伽玛关机敏感器需要在3m左右给出关机指令，本文重点关注着陆模拟器倾斜状态时在3m左右的计数频率变化规律，将3m左右处的静态特性曲线局部放大，不同倾斜角度时与水平状态时的计数频率差异如图6～8所示。

从图6～8中不同倾斜角度与水平状态的频率计数差异分析可以得出：1）绕Y轴倾斜不同角度时引起的计数频率偏差较小且基本一致；2）绕Z轴倾斜时引起的计数频率偏差比绕Y轴倾斜时普遍偏大，且随着倾斜角度的增大偏差逐渐增大；3）绕 Z轴负角度倾斜时的计数频率均小于水平姿态时的计数频率，绕Z轴正角度倾斜时的计数频率均大于水平姿态时的计数频率。

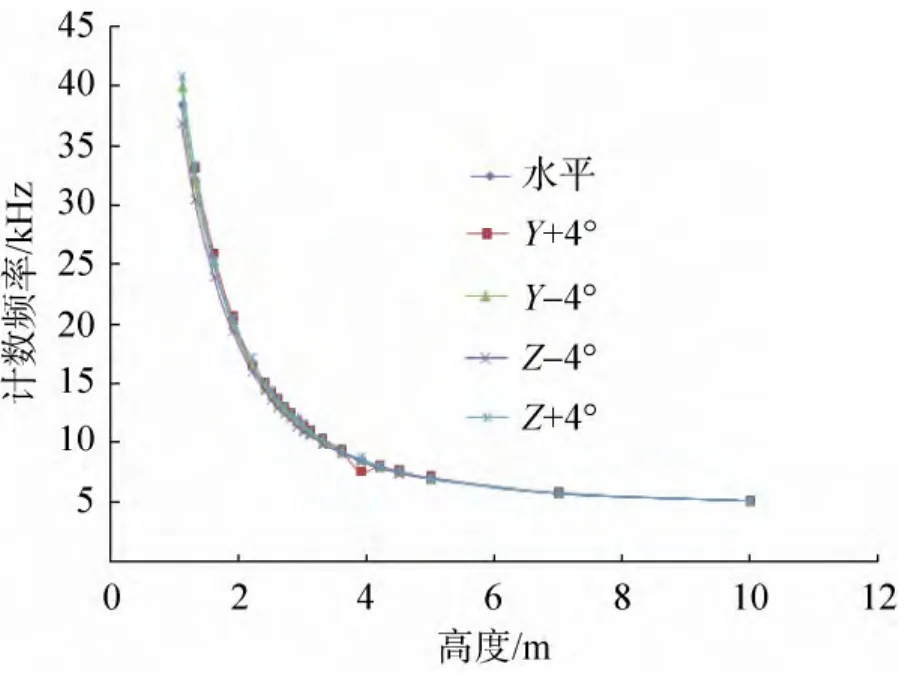
图3 倾斜4°时的静态特性曲线Fig. 3 The characteristic curve when the tilt angle is 4 degree

图4 倾斜8°时的静态特性曲线Fig. 4 The characteristic curve when the tilt angle is 8 degree

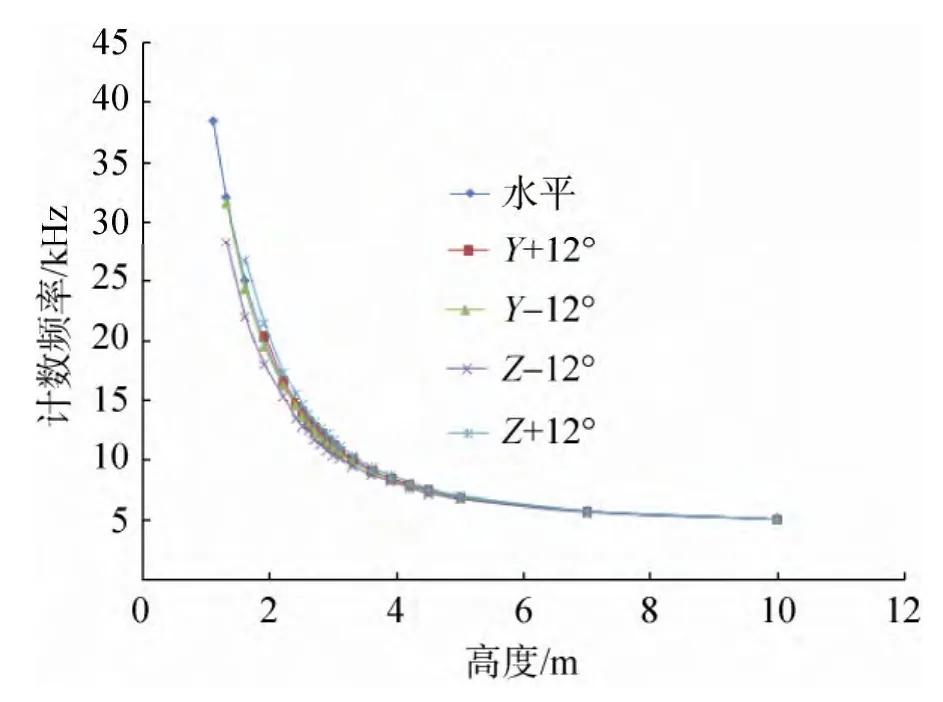
图5 倾斜12°时的静态特性曲线Fig. 5 The characteristic curve when the tilt angle is 12 degree

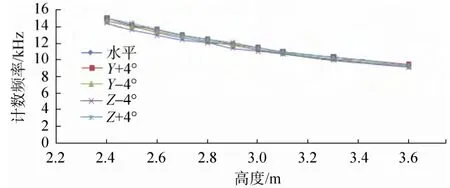
图6 倾斜4°与水平状态计数频率差异Fig. 6 The comparison of frequency between the horizontal and 4 degree tilted states

图7 倾斜8°与水平状态计数频率差异Fig. 7 The comparison of frequency between the horizontal and 8 degree tilted states

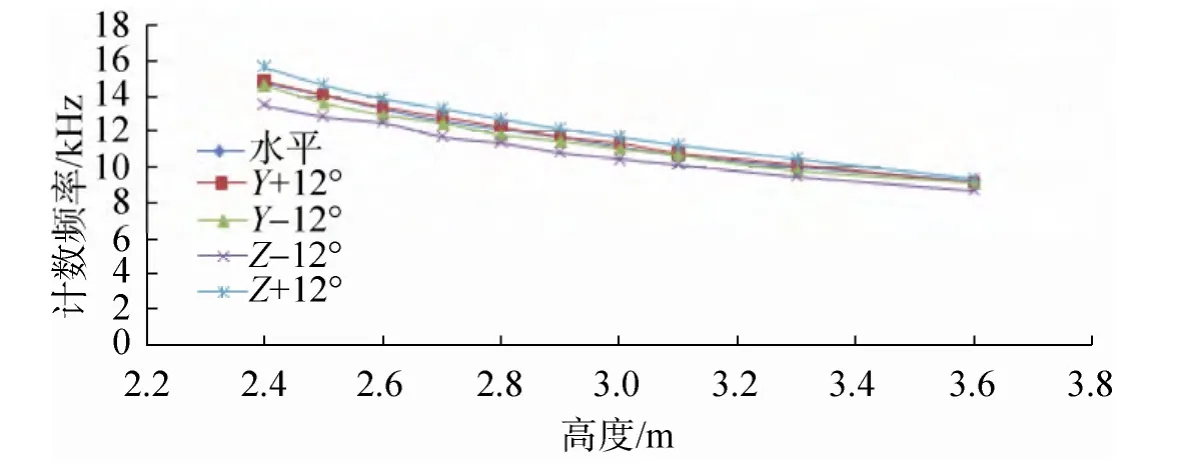
图8 倾斜12°与水平状态计数频率差异Fig. 8 The comparison of frequency between the horizontal and 12 degree tilted states

为了确定不同倾斜状态对关机高度的具体影响程度，将伽玛关机敏感器按水平状态静态特性数据调试关机高度，再利用绕Y轴和绕Z轴不同角度倾斜时获得的静态特性数据对伽玛关机敏感器进行关机高度测试，得到不同倾斜角度时的关机高度情况（如图9～10所示），并得到不同倾斜姿态引起的测高精度偏差见表1。

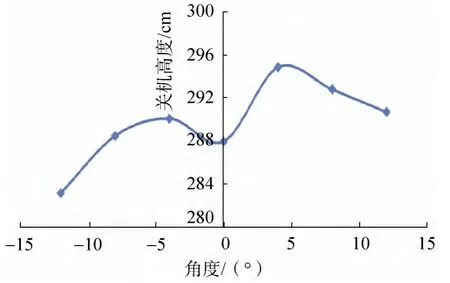
图9 绕Y轴不同倾斜角度时关机高度Fig. 9 The shutdown height with different tilt angle around Y-axis

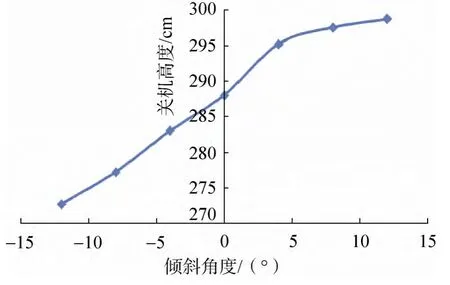
图10 绕Z轴不同倾斜角度时关机高度Fig. 10 The shutdown height with different tilt angle around Z-axis

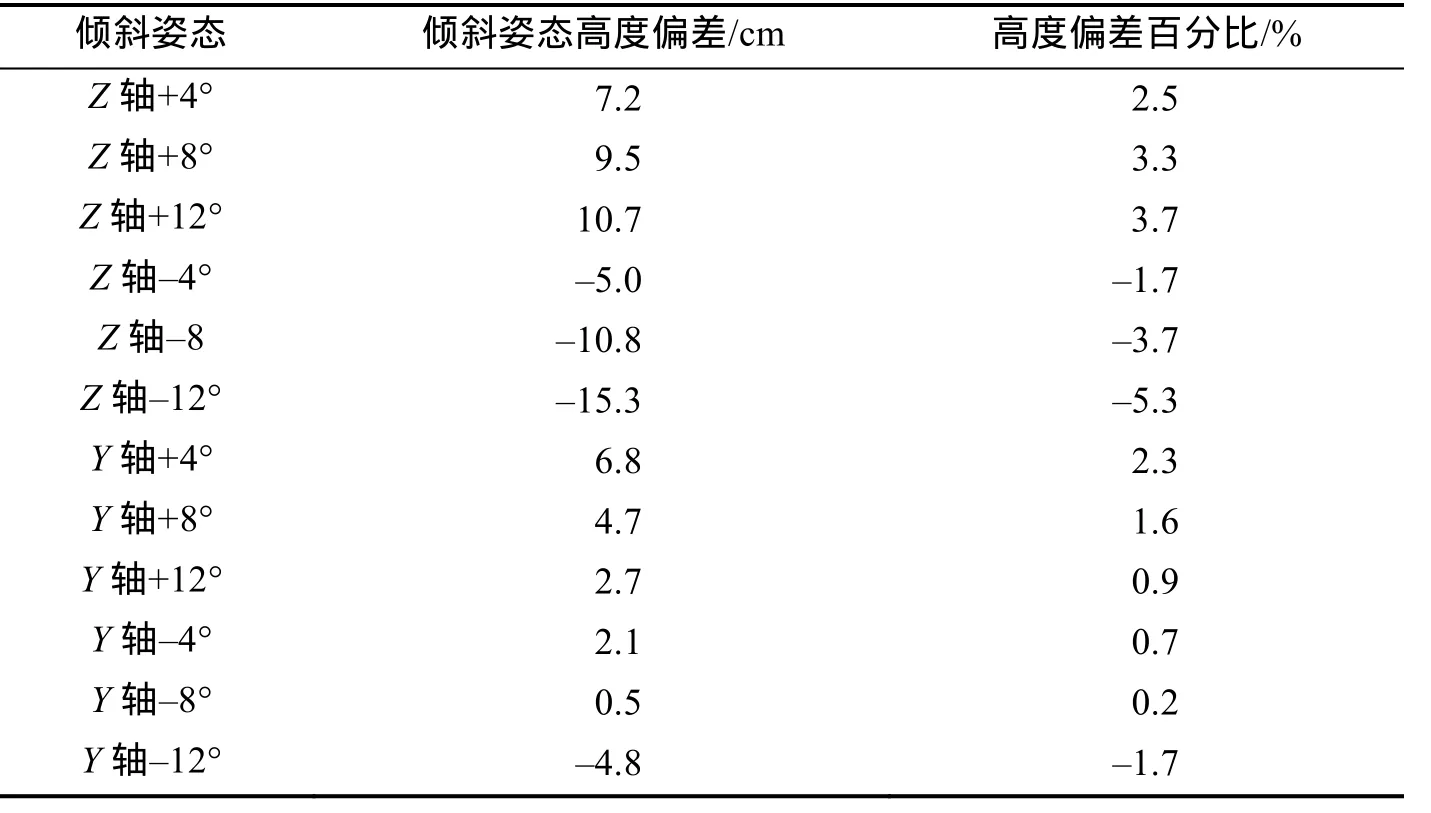
表1 不同倾斜状态时测高精度偏差Tab. 1 The altitude error with different tilt positions

从图9～10显示的关机高度变化趋势可以看出，在绕Y轴正角度或负角度倾斜时，随着倾斜角度增大，关机高度分别都呈递减趋势，但在–12～+12°的变化区间内，关机高度不是单调变化的，而绕Z轴倾斜时关机高度则随倾斜角度的变化呈单调特性，绕Z轴倾斜–12°时引起的关机高度偏差最大。

实际上，基于γ射线的测距应用技术主要是将γ射线与物质相互作用中的康普顿散射形成的γ光子作为计数应用，γ光子的计数率与距离的平方成反比，不同倾斜状态使得 γ光子的辐射面积、接收处理器的接收角度以及发射器和接收处理器与着陆面的距离均发生了变化，从而引起计数频率发生差异。

由于发射器和接收处理器安装于同一侧，当着陆模拟器绕Y轴和Z轴进行不同角度倾斜时，发射器和接收处理器的升降状态不同。当绕Y轴正角度倾斜时，发射器升高，接收处理器降低；当绕Y轴负角度倾斜时，发射器降低，接收处理器升高。当绕Z轴负角度倾斜时，发射器和接收处理器同时升高，可能引起计数率值偏小；当绕Z轴正角度倾斜时，发射器和接收处理器同时降低，可能引起计数率值偏大。

4 结论

从着陆模拟器不同倾斜状态的精度验证试验结果可以看出，在着陆模拟器倾斜角度不大于 12°条件下，绕Z轴倾斜时的计数频率和关机高度变化随倾斜角度变化呈单调特性，绕Y轴倾斜时的计数频率和关机高度变化则不具有单调性，绕Z轴倾斜–12°时引起的计数率和关机高度偏差最大，不同倾斜状态引起的测高精度误差绝对值不大于5.3%。

（

）

[1] 蒋万松, 黄伟. 月球着陆器着陆稳定性仿真分析[J]. 航天返回与遥感, 2010, 31（6）: 16-22. JIANG Wansong, HUANG Wei. Simulation Analysis of Landing Stability for Lunar Lander[J]. Spacecraft Recovery & Remote Sensing, 2010, 31（6）: 16-22. （in Chinese）

[2] 黄昊, 张熇 . 月球软着陆探测的着陆敏感器选择及相关问题分析[C]. 中国宇航学会深空探测技术专业委员会第三届学术会议, 2006. HUANG Hao, ZHANG He. The Choice of Landing Sensors and Analysis of Lunar Landing Exploration[C]. The Third Conference of Committee of Deep Space Exploration Technology, Chinese Society of Astronautics, 2006. （in Chinese）

[3] Dunn Catherine, Prakash Ravi. A Terminal Descent Sensor Trade Study Overview for the Orion Landing and Recovery System[R]. IEEEAC Paper 2038, NASA 20110007184, California: Jet Propulsion Laboratory, 2011.

[4] Amzajerdian Farzi, Petway Larry B, Hines Glenn D. Lidar Sensors for Autonomous Landing and Hazard Avoidance[R]. NF1676L-16053, NASA 20140002742, Hampton Virginia: American Institute of Aeronautics and Astronautics, 2014.

[5] Fassett C I, Head J W, Kadish S J. Lunar Impact Basins: Stratigraphy, Sequence and Ages from Superposed Impact Crater Populations Measured from Lunar Orbiter Laser Altimeter （LOLA） Data[R]. GSFC-E-DAA-TN8789, NASA 20130014881, Greenbelt MD: NASA Goddard Space Flight Center, 2013.

[6] Glenn Hines, George Lockard, Bruce Barnes. Navigation Doppler Lidar Sensor for Precision Altitude and Vector Velocity Measurements: Flight Test Results[C]. Sensors and Systems for Space Applications, Orlando, Florida: SPIE, 2011.

[7] Chen C W, Pollard B D. A Radar Terminal Descent Sensor for the Mars Science Laboratory mission[C]. Aerospace Conference, Montana: IEEE, 2009.

[8] Braun R D, Manning R M. Mars Exploration Entry, Descent and Landing Challenges[R]. NASA 20060050781, Pasadena: Jet Propulsion Laboratory, 2006.

[9] Lands J F. Development of a Terminal Landing Rocket System for Apollo-type Vehicles [J]. AIAA Journal of Pacecraft and Rockets, 1967, 4（3）: 333-338.

[10] Rogers W F. Apollo Experience Report-lunar Module Landing Gear Subsystem[R]. NASA-TN-D-6850, NASA 19720018253, Washington D.C.: Johnson Space Center, 1972.

[11] 黄伟. 反推发动机点火控制高度及其随机偏差分析[J]. 航天返回与遥感, 2002, 23（3）: 6-10. HUANG Wei. An Initial Ignition Altitude for Retrorocket and its Random Deviation Analyzing[J]. Spacecraft Recovery & Remote Sensing, 2002, 23（3）: 6-10. （in Chinese）

[12] 安毓英, 曾晓东. 光电探测原理[M]. 西安: 西安电子科技大学出版社, 2004. AN Yuying, ZENG Xiaodong. Photoelectric Detection Principle[M]. Xi’an: Xidian University Publisher, 2004. （in Chinese）

[13] 任明岩, 胡海, 孙金英. 基于光电倍增管的光子计数仪设计[J]. 今日电子, 2007（2）: 72-73. REN Mingyan, HU Hai, SUN Jinying. Design of Photon Counting Devices Based on Photomultiplier Tube[J]. Electronic Products, 2007（2）: 72-73. （in Chinese）

[14] 王挺峰. 光子计数用光电倍增管的外围工作电路[J]. 光机电信息, 2009, 26（2）: 39-43. WANG Tingfeng. Working Circuit of PMT in Photon Counting Systems[J]. Ome Information, 2009, 26（2）: 39-43. （in Chinese）

[15] 张楠, 吴世通, 沈超. γ源辐射角度对光子高度计性能的影响分析[J]. 航天返回与遥感, 2014（6）: 37-41. ZHANG Nan,WU Shitong, SHEN Chao. Analysis of Effect of γ Radiation Angle on the Photons Altimeter[J]. Spacecraft Recovery & Remote Sensing, 2014（6）: 37-41. （in Chinese）