月面探测中的单目相机成像测量方法

李立春 许颖慧 孟彦鹏 张祖丽 张伟 万文辉 周建亮

（1 北京航天飞行控制中心，北京 100094）

（2 国防科学技术大学 航天科学与工程学院，长沙 410073）

（3 中科院遥感与数字地球研究所 遥感科学国家重点实验室，北京 100101）

0 引言

在月球及火星等地外天体表面着陆探测工程中，探测器通常搭载多类单目相机，如“嫦娥三号”任务中的降落相机、监视相机、地形地貌相机等成像设备，这些相机不具备直接构成双目视觉系统进行精确测量的条件。如何从单目成像中实现探测信息提取，以支持探测器着陆定位及就位探测是测控系统需要事先考虑并亟需解决的重要问题之一[1-2]。

运用降落过程的序列成像对月面着陆点定位是典型的单目成像应用过程，文献[3]根据着陆区近似平面的条件提出了基于平面单应的着陆成像引导方法。在飞行器制导与导航定位工程中的单目成像的应用非常多[4-6]，其中的难点是实时图像与基准图的配准问题[7-8]。在天体着陆后就位探测的探测器定位方面，传统的无线电测量方法精度较低，而且不能直接提供相对于任务规划基准图的定位[4,9-10]，通常借助于单目成像或者双目成像的视觉处理方法。

为了解决单目成像分析的难题，拓展其在着陆与探测中应用，本文开展探测过程中单目成像工作模式及图像处理方法的研究，提出相应工作模式下的图像测量方法，以解决基于降落相机成像的飞行器定位问题和天体就位探测条件下基于场景约束的测量问题。

1 基于序列成像的图像融合及定位方法

天体表面软着陆的避障、滑行、着陆过程中，通常用探测器搭载的降落相机对着陆区域进行连续动态的序列成像，着陆降落轨迹及其降落成像过程如图1所示。降落过程连续成像之间图像具有较大的重叠区域，随着飞行高度的降低，实时成像的视野范围变小，同时成像的空间分辨率将升高。

通过实时成像进行飞行器定位的基础是实时图与基准图的匹配，随着飞行高度降低和成像视野的变小，在基准图上与实时成像相匹配的配准区域将变小，通常情况下将无法实施匹配定位。为解决该问题，本文提出一种基于序列图像的大视野图像融合生成及成像位置确定方法。

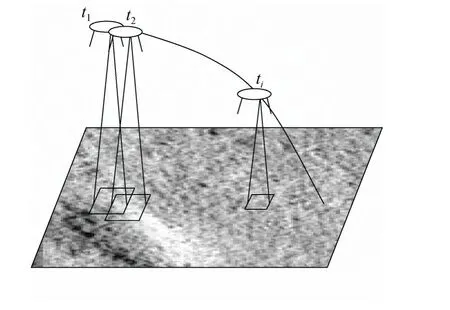
图1 飞行器着陆过程成像示意图Fig. 1 The imaging of target area on the process of spacecraft landing

1.1 大视野图像融合生成

将降落过程的整个着落区域作为研究对象，则成像的空间视野满足近似平面约束。该条件下，若连续两次时刻t1、t2成像I1、I2之间的单应矩阵为H12，则两图对应点之间满足以下关系式：

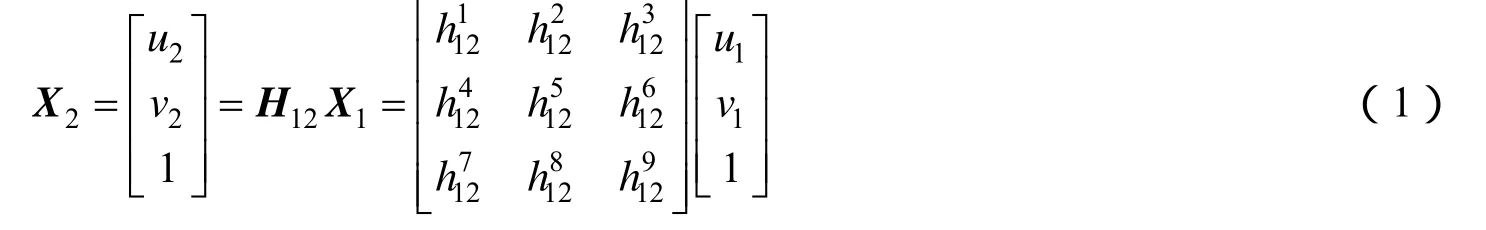
降落过程中相邻两次的高高度成像和低高度成像的图像分别为Ii和Ii-1，则低高度的高分辨率成像相对于低分辨率图像将缺少图像范围Ii′-1，根据式（1）的近似平面的单应关系，该图像上的缺失范围Ii′-1可以从Ii上通过Ii与Ii-1的单应关系转移得到，从而实现大视野图像合成，如图2所示。从降落过程最高位置成像I0到最低位置成像IN，逐次进行上述图像扩充过程，最终可以得到与IN图像高分辨率等分辨率的大范围图像。高分辨率大图在着陆点附近具有高分辨率，同时具有整个着陆区的大视野大范围，是着陆点定位、着陆区态势分析与任务规划的数据基础。

利用上述方法，对“嫦娥三号”的降落相机在100m和30m两个不同高度上的成像进行单应转移矩阵解算，基于该单应将100m高度的图像转换后与30m高度成像进行融合，如图3所示，图中虚线范围内为30m高度的高分辨率图像。

图2 大视野图像生成示意图Fig. 2 The generation process of an image with wide view

图3 降落相机100m高度与30m高度成像数据融合Fig. 3 The merged image from images with the imaging height of 100m and 30m

1.2 基于降落相机成像的着陆过程飞行器定位方法

降落相机图像用于探测器着陆定位的基本原理是，首先获取着陆过程的降落相机图像及其对应基准图的初始粗略位置；第二步将降落相机图像特征点与着陆区基准图特征点进行精确匹配定位，确定特征点的三维位置；最后根据特征点的空间位置反向推导成像时刻探测器的位置。初始粗略位置通常可以通过无线电或者惯性导航方法获得。用于匹配的基准图是降落区域的正射影像图，而降落相机的降落过程实时图像是倾斜成像，它与正射图之间存在缩放和剪切等变形，两图的匹配采用基于Forstner特征提取与SIFT不变性匹配算法联合实现。

（1）特征点提取与匹配

着陆区域图像上的典型纹理和地形特征在不同图像间表现稳定，根据这一特点，本文提出了基于多尺度Forstner算法的特征提取与匹配方法。Forstner特征提取算法通过计算各像素的Robert梯度和灰度协方差矩阵，利用两个兴趣值来选择特征点[11]。在实时图和基准图的初始位置区域提取到特征点后，借鉴David G. Lowe的SIFT多尺度特征描述方法，分别对两图上的特征点建立不变性特征向量作为后续匹配的基础。特征向量的构建包括以下主要步骤来实现：①计算特征点邻域范围所有点的梯度，统计获取区域的主方向；②以主方向作为参考方向，消除特征分布的旋转差异；③通过子区域划分和梯度统计值建立向量描述。向量构建的具体实现可参考文献[12]。

特征匹配点通过特征距离比较和最小二乘方法两步实现。特征距离比较方法的匹配过程是：首先对每一个特征点建立特征向量，第二步是计算待匹配点与每一个候选特征点之间的特征距离，最后对这些特征距离进行比较，选择距离最小的作为同名匹配点。特征距离dV计算公式为：

式中 V和V′为待匹配两图中特征点的不变性向量描述；vi和vi′为其向量的分量。

基于特征向量描述和特征距离比较的匹配方法能够消除图像旋转的影响，可以保证点匹配的鲁棒性。在此基础上利用最小二乘方法实现特征点的精确匹配[13]。

（2）飞行器位置计算

着陆过程中对着陆区域的成像模型可用图像点p（u,v）、像点对应的三维空间物点 P（X,Y,Z）以及相机参数三者之间的光束共线方程来描述，见式（3）。

式中 （u,v）表示实时成像图像特征点坐标值；fu、fv分别表示相机在横轴和纵轴方向的等效焦距；（u0,v0）表示图像主点位置；R、T分别表示在空间坐标系中相机的姿态参数和位置参数；λ为成像的深度因子，表示空间物点在相机成像坐标系的光轴方向的坐标值。由于基准图是正射影像图，式中三维空间点的X，Y坐标通过特征点在基准图像的图像坐标直接获得，而Z坐标根据该点的X，Y坐标从地形数据库查询获得。

着陆过程飞行器定位是根据着陆过程实时图特征点与基准图同名点配准关系进行逆向求解，其对应的数学模型可描述为，已知N个三维控制点及其像点，根据计算机视觉的PNP问题[14]，这N个点提供了 N个形如式（3）的方程，从而可以构成方程组解算飞行器搭载相机的位置、姿态，实现位姿参数计算，见图4。

图4 基于飞行器成像的位姿计算原理示意图Fig. 4 The diagram of pose and position calculating from image

本文对基于控制点及其成像的位置姿态计算进行了仿真试验，试验中的成像参数为：图像分辨率为1 024像素×1 024像素，焦距1 500像素，像素尺寸为8μm，成像距离300m，成像空间分辨率约0.2m。仿真相机在设定的位置姿态上对7个三维空间点进行成像，并对像点添加均方差为0.5像素的定位误差，根据像点及其对应的三维空间点构建PNP问题对位置姿态进行解算作为测量值，100次试验结果统计值见表1。试验结果表明了方法的有效性。

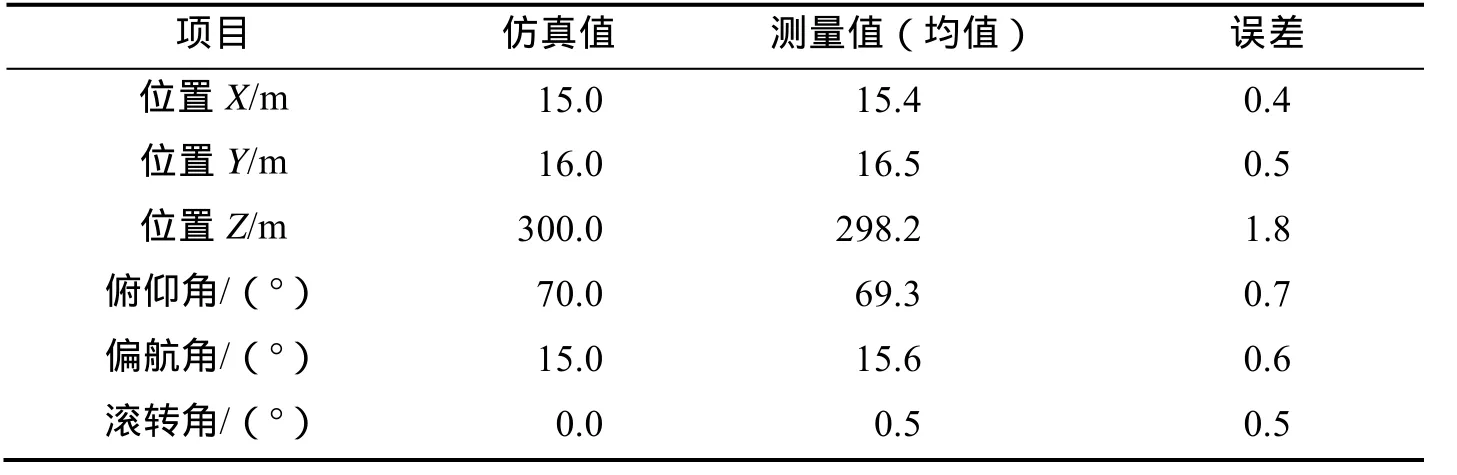
表1 基于控制点的位姿计算实例Tab. 1 Example of pose and position calculation from control points and its images

2 场景约束的单目成像测量方法

探测器着陆后，其搭载的单目相机可以对周围环境进行监视勘察，当探测器位置姿态已知、以及着陆区近似平面场景条件下，可以进一步利用单目视觉实现目标的测量定位，完成就位探测视野的定量分析。图5给出了平面场景条件下单目相机成像模型的示意图，图中 OC-XCYCZC为成像的相机坐标系，OW-XWYWZW是测量的参考坐标系，称为世界坐标系，π是成像场景平面。

考察单目视觉对近平面场景成像测量，该平面场景内单目相机位置姿态已知，则目标与其成像的投影关系用式（3）表示，将式中内、外参数项合并后可写为式（4）

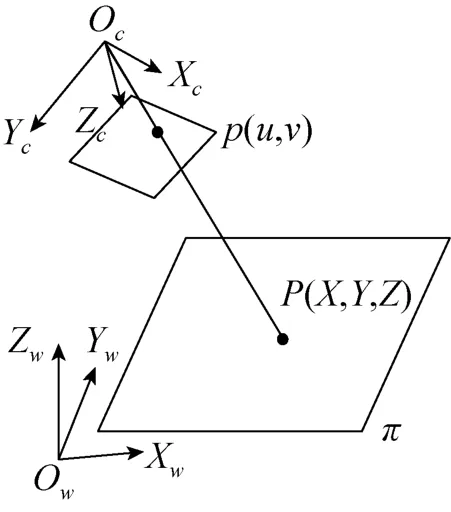
图5 基于平面的单目相机成像模型Fig. 5 The projection model of planar scene imaging

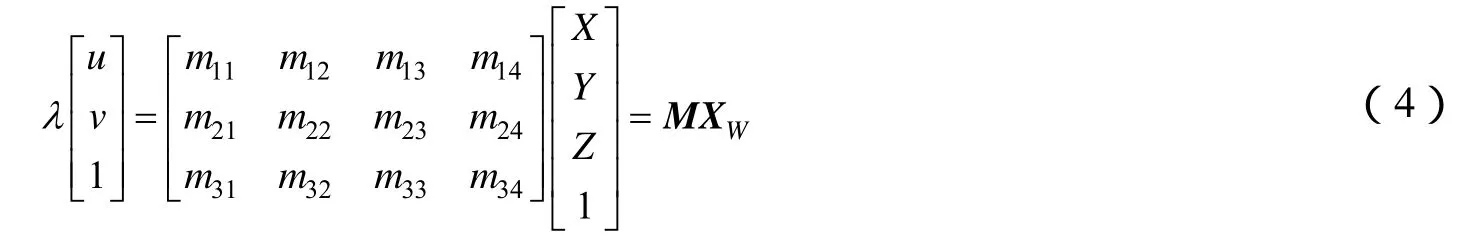
式中 M 表示三行四列的投影矩阵，可根据相机的内外参数计算[15]；XW为成像点在世界坐标系的齐次坐标值矩阵。

则根据式（4），不难得到关于像点与物点的关系，式（5）表示了相机系的像点转换到世界坐标系后投影成像的直线方程。

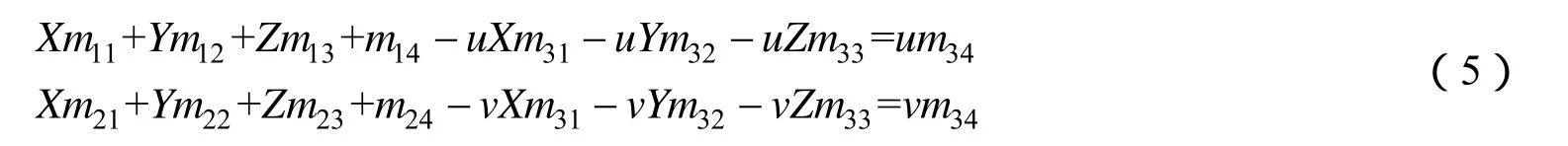
在世界坐标系下平面方程π可表示为：

式中 a、b、c、d为平面方程的系数。

将平面方程与成像光线方程联立，可得到计算目标点位置的关系式：

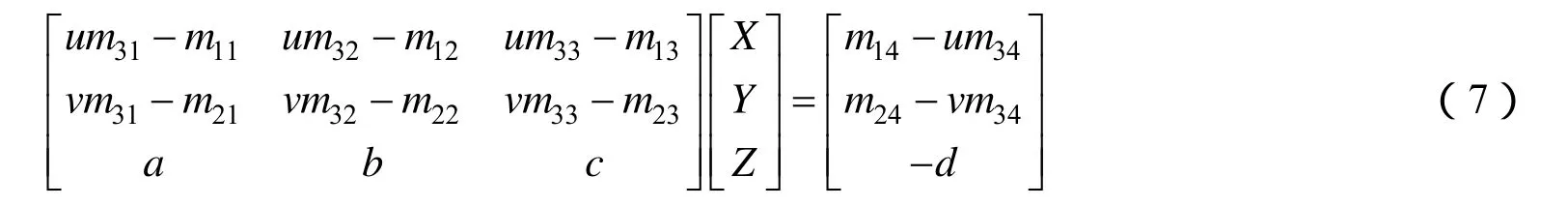
利用平面方程及已知的像点坐标作为输入，从上式可以求解得到像点所对应空间点的坐标（X,Y,Z），从而完成平面点位置计算。

基于该方法，对“嫦娥三号”任务的着陆器监视相机成像进行了目标位置计算实验，着陆器装载的监视相机的安装位置与姿态为已知参数，则根据着陆器的着陆姿态可以得到监视相机距月面高度以及相对月面姿态。典型配置下的监视相机成像示意见图 6。基于该配置参数，对监视相机视野内平面场景进行了目标位置测量与标注，成功应用于实际任务中的月球车驶离方式决策，如图7所示。

图6 监视相机配置示意图Fig. 6 The diagram of surveillance camera configuration

图7 监视相机成像视野目标测量结果图Fig. 7 The results of measurement labelled on the image of surveillance camera

3 基于合作目标的投影深度与方位测量方法

在月面巡视过程中，通过月球巡视车与着陆器互拍，各自获取了对方的影像，提供了目标状态判断的定性信息。由于巡视车及着陆器的三维结构为已知信息，在远距离成像条件下，成像模型可以用弱透视投影来近似，该条件下，根据已知的三维结构及其成像则可以实现目标位置、方位的定量估计。

月球巡视车与着陆器之间距离相对于其自身三维尺度足够大时，互拍成像过程可以简化为弱透视投影成像，这时，目标可作为位于垂直于光轴的物理平面上，应用单目视觉的几何相似法进行测量。在目标本身尺寸相对其到相机光心距离很小的条件下，目标上各点的深度可以用一共同的深度因子近似，这个值一般取物体质心的深度d，此时透视投影模型可近似为

式中 d表示目标点在光轴方向的成像距离；Xc、Yc表示目标点在成像坐标系两个坐标轴上的坐标值；x、y表示像点在两个图像坐标上的值；f是成像焦距。

这种近似可以看作两个阶段投影的合成，如图 8所示。

第1步，所有目标点按平行于光轴的方向正投影到假想图像平面I′上；第2步，再按透视投影模型将假想平面投影到图像I上，这一步实际是全局比例缩放，因此弱透视投影也称为比例正射投影。弱透视投影条件下，成像目标点的位置变化与其成像点的变化可由式（9）表示，则成像深度（目标距离）估计可由式（10）给出：

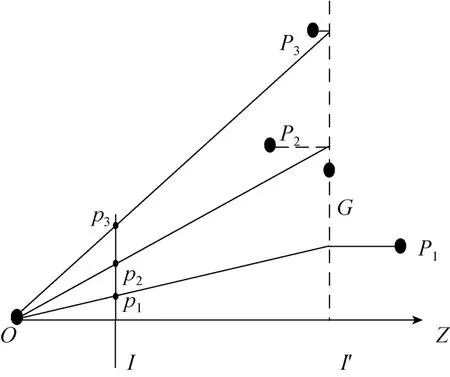
图8 弱透视投影模型Fig. 8 The model of weak perspective projection

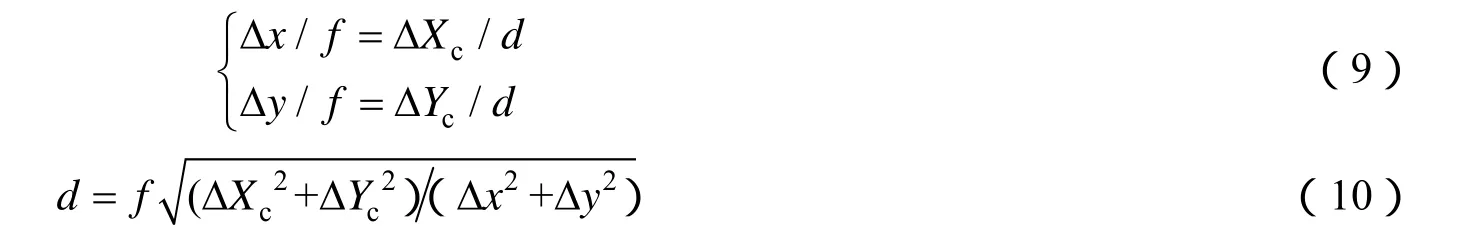
根据成像关系，在相机系下目标的横轴方向的偏航角度φ和纵轴方向的俯仰角度θ由下式给出：

根据弱透视关系，图9给出了月面巡视车对着陆器成像及其基于特征选点的测量示意图。图中O点是成像主点，S1、S2两点分别是着陆器主体边缘间距最大点，C点是着陆器质心，则利用S1、S2两点计算得到着陆器相对巡视车的距离，利用C点计算着陆器相对巡视车的方位信息。

图9 基于着陆器结构的目标距离测量示意Fig. 9 The diagram of distance measurement for landing spacecraft based on its structure and image

4 结束语

以月面着陆与就位探测过程中几类相机成像的应用背景，根据工程中特定的单目成像条件及应用环境，提出降落相机序列成像大场景高分辨率图像生成方法，在此基础上实现了基于图像特征点匹配与解算的着陆过程飞行器定位方法；利用成像位姿信息与平面场景约束关系，实现了应用单目成像的目标测量；利用远距离成像的条件，基于目标结构信息实现了目标距离与方位估计。对论文所提出方法结合“嫦娥三号”任务着陆降落相机图像与就位探测中监视相机成像进行了验证，结果表明该方法在月面探测中提供了具有应用价值的定量测量结果，有力支持了飞行探测任务实施。

（

）

[1] 张洪华, 梁俊, 黄翔宇, 等. 嫦娥三号自主避障软着陆控制技术[J]. 中国科学: 技术科学, 2014, 44（6）: 559-568. ZHANG Honghua, LIANG Jun, HUANG Xiangyu, et al. Autonomous Hazard Avoidance Control for Chang'e-3 Soft Landing[J]. Science China: Technology Science, 2014. 44（6）: 559-568. （in Chinese）

[2] 田林, 戚发轫, 果琳丽, 等. 载人月面着陆地形障碍探测与规避方案研究[J]. 航天返回与遥感, 2014, 35（6）: 11-19. TIAN Lin, QI Faren, GUO Linli, et al. Study of Terrain Hazard Detection and Avoidance Scheme for Human Lunar Landing[J]. Spacecraft Recovery & Remote Sensing, 2014, 35（6）: 11-19. （in Chinese）

[3] 李立春, 周建亮, 孙军, 等. 应用单应诱导视差的探测器月面着陆平面选择方法[C]. 第十届深空探测全国学术会议, 太原, 2013: 284-289. LI Lichun, ZHOU Jianliang, SUN Jun, et al. A Lunar Surface Landing Position Selection Method Based on the Parallax Induced by Plane[C]. The 10ThConference of Deep Space Exploration, Taiyuan, 2013: 284-289. （in Chinese）

[4] 王大轶, 黄翔宇. 深空探测自主导航与控制技术综述[J]. 空间控制技术与应用, 2009, 35（3）: 6-13. WANG Dayi, HUANG Xiangyu. Survey of Autonomous Navigation and Control for Deep-space Exploration[J]. Aerospace Control and Application, 2009, 35（3）: 6-13. （in Chinese）

[5] JOHNSON A, HUERTAS A, WERNER R, et al. Analysis of On-Board Hazard Detection and Avoidance for Safe Lunar Landing[C]. 2008 IEEE Aerospace Conference, Big Sky, MO, Mar. 2008.

[6] 王海涛, 马建华. 基于降落图像的安全着陆点选择技术研究[J]. 航天返回与遥感, 2012, 33（4）: 13-18. WANG Haitao, MA Jianhua. Safe Landing Site Selection Based on Landing Image[J]. Spacecraft Recovery & Remote Sensing, 2012, 33（4）: 13-18. （in Chinese）

[7] 丁萌, 曹云峰, 吴庆宪. 月球探测器着陆中基于被动图像的着陆场搜索及斜坡估计[J]. 宇航学报, 2009, 30（6）: 2258-2264. DING Meng, CAO Yunfeng, WU Qingxian. Passive Image-based Safe Landing Site Searching and Slope Estimation in Probe Landing[J]. Journal of Astronautics, 2009, 30（6）: 2258-2264. （in Chinese）

[8] ALAN L S, ADREW E J. Terrain Hazard Detection & Avoidance during the Descent & Landing Phase of the Altair Mission[R]. NASA Johnson Space Center, Jet Propulsion Laboratory, 2010.

[9] JOHNSON A E, MONTGOMERY J F, MATTHIES L H. Vision Guided Landing of an Autonomous Helicopter in Hazardous Terrain[C], IEEE International Conference on Robotics & Automation, New York, 2005: 218-223.

[10] PRASUN N D. Entry, Descent, and Landing Performance of the Mars Phoenix Lander[C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Hawaii, 2008: 18-21.

[11] FORSTNER W. A Feature Based Correspondence algorithm For Image Matching[C]. Proceedings of the Intern.Arch. of Photogrammetry and Remote Sensing，Rovaniemi, 1986, 26: 150-166.

[12] MORTENSEN E N, DENG Hongli, SHAPIRO L. A Sift Descriptor with Global Context[C]. Proceedings of International Conference on Computer Vision and Pattern Recognition, San Diego, USA, 2005, 184-190.

[13] LI Lichun, ZHANG Heng, FU Dan, et al. Image Matching Based on Epipolar and Local Homography Constraints[C]. Proceedings of SPIE, Beijing, Vol6833, 68330Z （2007）.

[14] LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: An Accurate O（n） Solution to the PnP Problem[J]. Int’l Journal of Computer Vision, 2009, 81（2）: 155-166.

[15] RICHARD H, ANDREW Z. Multiple View Geometry in computer vision[M]. Cambridge Univeristy Press, 2000.