基于微粒群技术的多分拣区产品存储的算法设计

陈彦如 杨 璐 魏朝恒 曾东红

1. 西南交通大学，经济与管理学院，成都 610031

2. 西南交通大学，交通运输与物流学院，成都 610031

0 引 言

为了提高分拣效率，许多配送中心分别设置了分拣区（Forward area）和存储区(Reserve area)。分拣区用于快速分拣,存储区用于大量存储、补货及未指派至分拣区的产品的分拣。如何解决在有限的分拣区存放多少数量的何种产品，便形成了 FRP（the forward-reserve problem）—— 分拣区存储优化问题。

根据分拣区设置的数目可将 FRP问题分为单分拣区FRP与多分拣区FRP。目前单分拣区FRP的研究成果较为丰富[1-4]，由于该问题属于NP难问题，因此该问题的求解大多考虑启发式算法。而多分拣区FRP问题研究成果较少，同时因为涉及多个分拣区的协调优化，求解更为复杂。考虑到精确算法的局限性及微粒群算法在求解大规模组合优化问题的优势[5]，本文尝试设计求解多分拣区 FRP的微粒群算法，并用算例验证了该算法的有效性。

1 模型描述[6]

符号说明：

i——产品种类， i = 1 ,2,3,… ,I ；

j——存储方式， j = 1 ,2,3,…,J

k——分拣区， k = 1 ,2,3,…,K

Ck——分拣区k单位面积的建设成本；

Sk——分拣区k的空间；

aij——产品i以存储方式 j存储时，每单位可存储产品i的个数；

Di——产品i的需求量；

Cr——产品i以存储方式 j存储在存储区的分

ij

拣成本；

多分拣区产品存储模型可描述如下：

2 算法设计

微粒群算法（Particle Swarm Optimization，PSO）是美国心理学家Kennedy与电气师Barnhart在1995年提出的，其算法思想来源于对鸟群觅食这一生物现象的模拟。鸟群中的每一只鸟称为一个粒子，每一个粒子在空间搜索最优目标。粒子的行为受到两个方面的影响：一是自身最优位置，二是群体最优位置。在这两个因素下，粒子朝着最优的方向不断寻觅，而整个粒子群最终寻觅到的就是最优结果。PSO算法为每个粒子都定制了类似于鸟类运动的行为规则，从而使整个粒子群的运动表现出与鸟类觅食相似的特性，用于求解复杂的优化问题。具体的算法步骤如图1所示。

图1 微粒群算法流程Fig.1 Process of particle swarm optimization

2.1 粒子编码

本阶段需要对问题的可行解进行编码。考虑到将C种产品以J种存储方式放在K个分拣区，因此所设计的粒子总长度为C*J*K+C+K。粒子包括三个部分，第一部分长度为C*J*K，表示C种产品以J种方式在K个分拣区的存储方案。第二部分长度为C，表示C种产品的存储方式是否发生改变。第三部分长度为K,表示K个分拣区是否建立。

以C=4，J=2，K=3为例的编码如图2所示。

图2 粒子编码示例Fig.2 Coding pattern of a particle

其中第一部分010000100000000100000001由四段构成，每段对应一个产品，各段内每3位表示3个分拣区内的一种存储方式，该粒子的第一段 010000表示第一个产品以第一种存储方式存放在第二个分拣区内，第二段100000表示第二个产品以一种存储方式存放在第一个分拣区。由于每个产品只能以一种存储方式存放在一个分拣区，因此每段只能有一个值为1。第二部分0101表示4种产品的存储方式是否发生改变，如果为0，表示未改变，反之为1。该部分表示第2种和第4种产品的存储方式发生了改变。第三部分110表示3个分拣区的设置决策，即仅设置第一个和第二个分拣区。

2.2 初始化粒子群

给定各参数的初始值，在指定的优化范围内初始化粒子群中每个粒子的速度和位置；初始化加速因子c1、c2和其他相关参数。设每个粒子的个体最优值为pBesti。设种群的全局最优值为gBest。

因为每个粒子存在着诸多的属性，要想更好地描述粒子群的性质，需要首先声明一个粒子群的结构体。声明如下：

struct population //定义粒子群结构体

{

string str;//本粒子的解编码string sub1,sub2,sub3;

long X[100][2][5],V[100],Y[5];

long max1,max2,max3,fitness;//本粒子适应值string pstr;//历史最优粒子

long pfitness;//历史最优适应值

};

其中包含的属性分别有：粒子的编码、各决策变量的编码、各决策变量的存储数组、该粒子的适应值、该粒子历史最优解的编码以及该粒子的历史最优适应值。

按照粒子群结构体的特点，随机生成一定规模的具有多属性的粒子群。

2.3 粒子评价

判断粒子的质量优劣，主要依据模型的目标函数，即来进行。质量越优的粒子目标函数值越大。

2.4 更新最优值

如果更新后粒子的适应度值优于原来的值，则将新的适应度值作为该粒子的适应度值，新的粒子的位置作为该粒子的pBesti。如果更新后粒子的适应度值优于原来的全局最优 gBest，则将该粒子的位置作为新的全局最优gBest。

2.5 粒子位置与速度更新

粒子群中所有粒子的每一维在每一次迭代中都会有一个速度，因此每一次的迭代都会对该粒子的一系列属性进行更新操作。由于多分拣区 FRP产品存储为0—1整数规划问题，更新速度的计算不再是连续的计算，因此与一般的粒子群的更新有所区别。公式（5）即为当前粒子的速度公式：

式（5）不考虑前一次迭代中的速度，只考虑影响粒子速度的主要因子“自身认知”c1·ra n d()·(pBestij-Xij)和“社会认知”c2·ra n d ( )·(gBestj-Xij)。其中c1,c2分别为自身认知系数和社会认知系数，分别代表着自身历史和全局对当前速度的影响权重。rand（）为 0—1之间的随机变量，表示可能会出现的随机情况。pBestij为该粒子的历史最优组合，gBestj为该粒子群的全局最优组合。

为了使每次迭代后的Xij值只取1或者0，论文将速度转化为相应Xij取1或者0的概率。具体步骤是首先借助 sigmoid 函数将粒子速度的值映射到区间[0,1]，如式（6）所示：

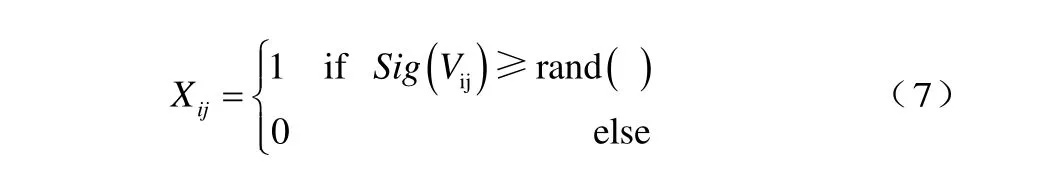
rand ()是一个随机数，从区间[0,1]随机产生。Sig(Vij)表表示位置Xij取1的概率，即sigmoid函数的变换并不是代表位Xij变化的概率，而只是代表位取Xij取 1的概率。综上所述，以此种步骤来完成粒子群速度的更新以及粒子各维度位的更新。

3 算例验证

某配送中心设有存储区与三个分拣区，在存储区中存储着配送中心每一品类的存货。现有A、B、C、D四种产品被分配到某个分拣区，现假设三个分拣区单位空间的建设成本相同，均为 10。每个产品的存储、分拣与补货作业操作均以托盘为单位，假设产品大小相同，产品的存储方式有2种：以第一种方式存储时，每个托盘每次可以存放10个产品；以第二种存储方式存储时，每个托盘每次可以存放20个产品。三个分拣区的存储容量分别为可以存储1 000，500，1000个单位。A、B、C、D四种产品的需求分别为226、238、287、259。四种产品在存储区、分拣区的分拣成本、处理成本与补货成本如表1至表4所示。

表1 产品在存储区的分拣成本Tab.1 Picking costs in a reserve area

表2 产品在分拣区的分拣成本Tab.2 Picking costs in a forward area

表3 产品处理成本Tab.3 Handling costs

表4 产品补货成本Tab.4 Replenishment costs

所设计的微粒群参数设置为：粒子群规模为20，迭代次数为10，认知系数和社会系数都为0.5。进行算法对比时，论文选取了CPLEX软件的Branch & Cut算法。为了更加客观的对算法进行验证，论文对算例独立运行了20次。两种算法的适应度与运行时间对比如图3所示。

图3 4个产品两种算法的适应度及计算时间对比Fig.3 Comparison of fitness value and computation time between PSO and Branch & Cut algorithms in the case of 4 products

论文同时对10、50、90个产品进行了测试（相关数据略），结果如图 4~6所示。当产品数为 50与90时，Branch & Cut算法已经无法在有效的时间内给出最优解。

图4 10个产品的两种算法适应度对比Fig.4 Comparison of fitness value between PSO and Branch & Cut algorithms in the case of 10 products

图5 50个产品微粒群算法的适应度和计算时间Fig.5 Comparison of fitness value and computation time between PSO and Branch & Cut algorithms in the case of 50 products

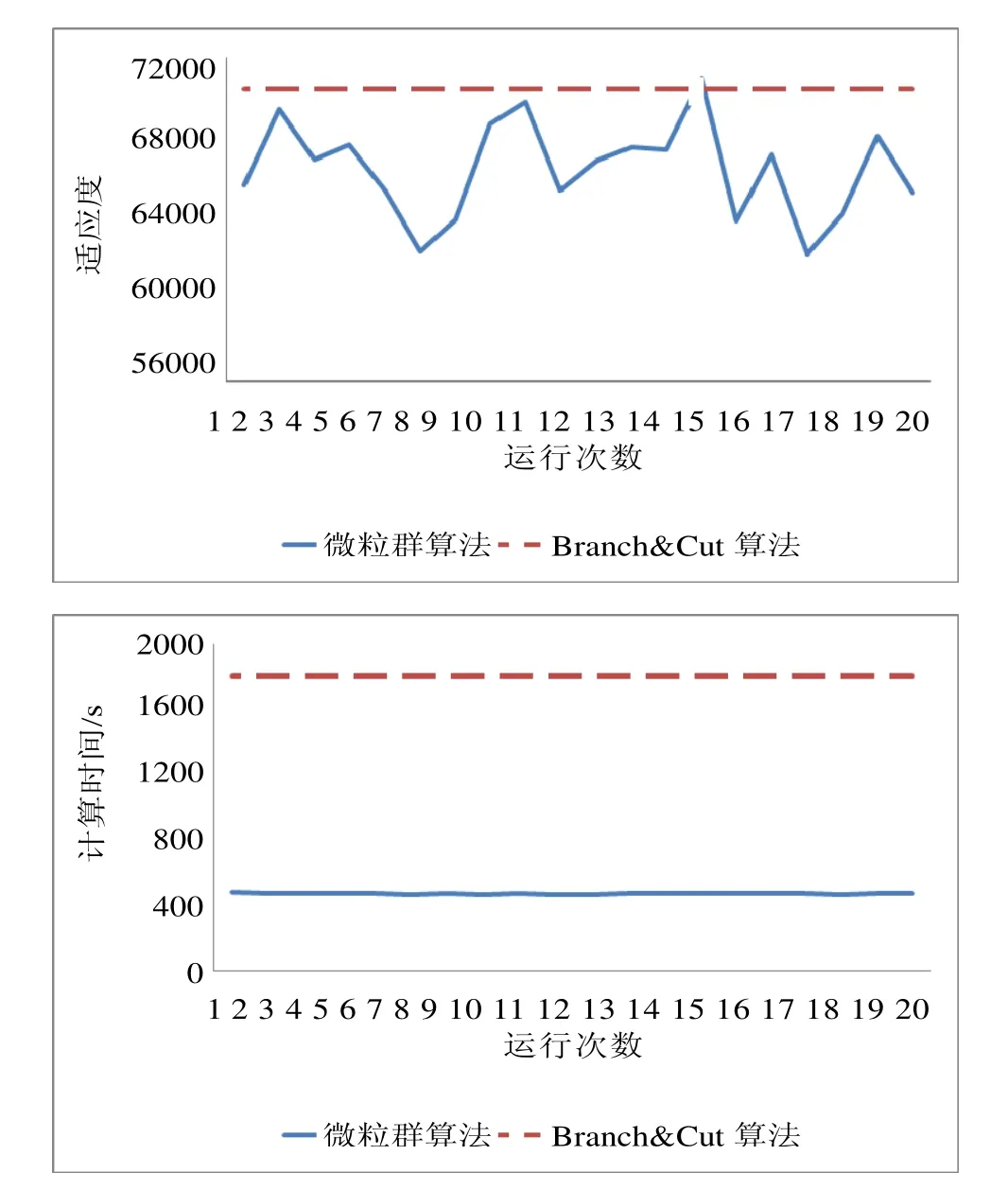
图6 90个产品的两种算法的计算时间对比Fig.6 Comparison of fitness value and computation time between PSO and Branch & Cut algorithms in the case of 90 products

从结果可以看出，产品数目较小时Branch & Cut算法可以以较短的时间找到最优解，但随着产品数目的增加，该算法所用时间大幅上升，尤其当产品数达到90时，该算法陷入“维度灾难”，只能人为终止算法。而本论文中所设计的算法，在产品规模增大后时间优势比较明显，可以在较短的时间内得到较满意的方案，甚至部分方案优于Branch & Cut算法所得的方案。

4 结 论

多分拣区的产品存储问题是典型的组合优化问题，随着问题规模的增加，求解会变得越来越困难。考虑到微粒群算法在求解组合优化问题的优势，本文设计了多分拣区产品存储的微粒群算法。通过和Branch & Cut算法相比较发现，当产品规模较小时，Branch & Cut算法的优势较为明显，但随着产品规模的增大，所设计的微粒群算法时间优势较明显，可以在较短的时间内得到较满意的解。

论文的研究结果有助于解决多分拣区的产品存储优化问题，但研究依然存在一定的局限性，如选用更大规模的产品数对算法进行验证，以及考虑和其他启发式算法进行组合以进一步提高求解效率，这将是论文进一步研究的方向。

[1] Heragu S S, Du L, Mantel R J, et al. Mathematical model for warehouse design and product allocation[J].International Journal of Production Research, 2005,43(2): 327-338.

[2] Van den Berg J P, Sharp G P, Gademann A N, et al.Forward-reserve allocation in a warehouse with unit-load replenishments[J]. European Journal of Operational Research, 1998, 111(1): 98-113.

[3] Frazelle E H, Hackman S T, Passy U, et al. The forward-reserve problem[M]. John Wiley & Sons,Inc., 1994.

[4] Gu J, Goetschalckx M, McGinnis L F. Solving the forward-reserve allocation problem in warehouse order picking systems[J]. Journal of the Operational Research Society, 2010, 61(6): 1013-1021.

[5] 谢晓锋, 张文俊, 杨之廉. 微粒群算法综述[J]. 控制与决策, 2003, 18(2):129-134.

[6] 陈彦如, 单翠, 蒋阳升, 等. 多分拣区 FRP的GA&SS算法设计[J/OL]. 重庆交通大学学报（自然科学版）, http://www.cnki.net/kcms/ detail/50.1190.U.20141205.1507.013.html