需求不确定条件下应急物资调度优化研究

陈钢铁 帅 斌

1. 西华大学，交通与汽车工程学院，成都 610039

2. 西南交通大学，交通运输与物流学院，成都 610031

0 引 言

最近几年以来，全世界突发性事件发生的频率越来越高，其危害程度越来越严重。灾害发生后，应急物资的调度受到应急管理部门和公众的高度关注。进行合理、科学的应急物资调度对减少人员伤亡和经济损失具有重要的理论和实际意义。随着信息技术的发展，公众通过信息网络等渠道迅速得到灾害信息，如果不在应急救灾和应急物资调度过程中考虑，很有可能使不良舆论导致严重的社会问题。国内外很多学者对应急物资调度问题进行了相关的深入研究。陈森等考虑路网的抢修和车辆的应急配送问题，并运用遗传算法对模型进行求解[1]。王旭坪等在建立模型中，建立最小化灾害损失和车辆调度费用为目标函数，考虑在运力不足的情况下进行物资调度[2]。陈钢铁等建立道路抢修和应急物资调度模型，采用启发式算法对模型进行求解[3]。陈钢铁等首先从损毁路网修复和救援物资 2个方面建立双层模型，从有限物资分配修复损毁路网和救援上进行优化分配，并通过路径优化时间最短来分配物资，使应急救援系统的损失最小化[4]。近年来很多学者针对不确定问题对扰动的稳定性进行优 化[5-7]。张玲等采用可调整鲁棒优化的方法对应急资源调度问题优化[8]。但是，现有的文献很少将道路损毁、修复的不确定，灾害发生后应急物资需求的不确定进行研究。因此，本文将路网阻断、修复及需求不确定结合起来建立应急物资调度的成本目标函数模型，同时采用启发式算法对模型进行求解。

1 模型建立

1.1 问题描述及参数假设

1）假设在一个区域发生突发性事件后，应急救援网络中的路网部分路段受到损毁，同时有多个灾害地点需要进行应急救援。

2）假设有应急管理部门对损毁路段进行修复，修复后有成本和收益。为未满足应急物资的惩罚成本。其中：id为应急救援点i配送应急物资的变动单位成本；ix为应急救援点拥有的应急物资量，iN∈；if为应急救援点i配送应急物资的固定单位成本；ir为 0-1变量，救援点i被选中为应急配送点时取值为1，否则为0，i∈N；yij为应急救援路网上节点i到 j配送的应急物资的量，i∈ N ,j∈ N1； ej为灾害点 j未满足应急物资的单位处罚价格； zj为灾害点 j，没得到满足时，补配的应急物资量， j ∈N1其中，N1为需要救援点集合，N1⊆N。

应急救援点的容量限制

式中：iC为应急救援点i处理应急物资的容量限制。

灾害发生前的应急救灾的成本预算

式中：G为灾害发生后应急配送成本的总额。

应急救援点应急配送的物资不能超出该点的容量

灾害点的需求应该尽量满足

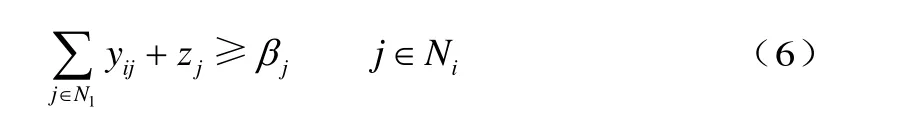
式中：βj为灾害点j的应急物资需求量，j∈N1。

非负约束

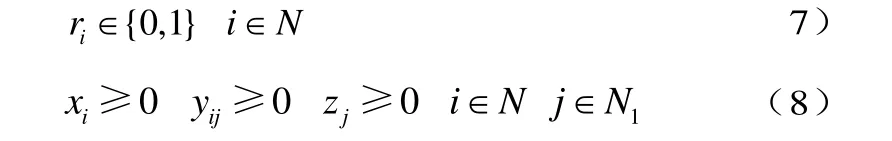
在灾害发生前，由于应急物资的需求量jβ的不确定性，灾害发生后灾害点的应急需求量jβ∈此处 βj为βj的下界， βˆj为最大偏差。

基于这种情况本文采用两个稳定性参数：Γ1为应急救援路网中路段的阻断数量，Γ2为灾害点的需求量估计值，则模型可转化为稳定性模型：

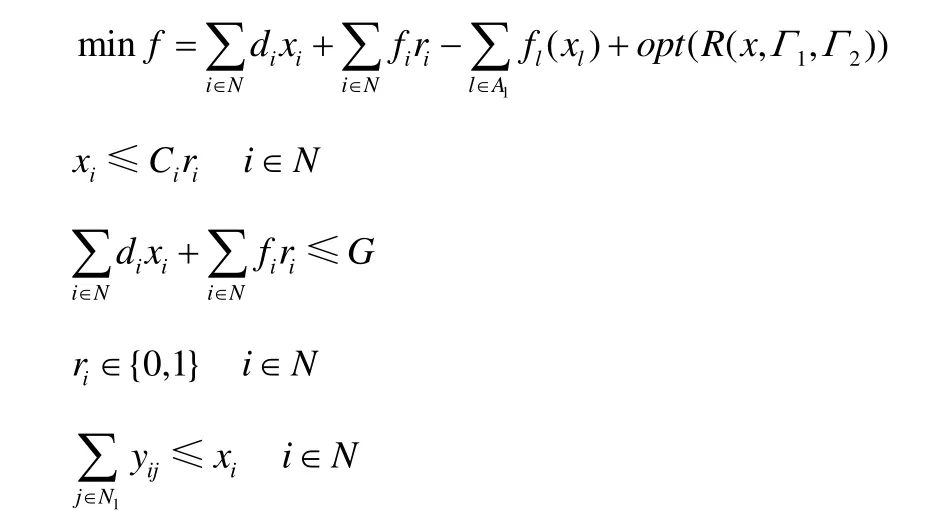
2 算 法

本文采用两阶段启发式算法对模型进行求解。第一阶段确定应急救援点数量，根据一定的规则每次迭代则增加一个应急救援点，找到应急救援点集合而且能满足模型中的约束条件；第二阶段寻找需求及应急救援路网中断的不确定性的最优调度方案时，则停止迭代。

Step 1：第1阶段利用启发式算法确定应急救援点的选址和数量及覆盖范围；

Step 2：第2阶段的个体中，利用覆盖率为启发式规则（寻找需求及应急救援路网中断的不确定性的最优调度方案时）产生M；

Step 3：针对第2阶段中的每一个个体k，确定每一个个体的适应值kj；

Step 4：对第2阶段进行选择：第2阶段中每一个个体被选中的概率为kp；采用蒙特卡洛法进行判断第2阶段的个体保留；

Step 5：对筛选后的第2阶段的个体进行交叉和变异；

Step 6：对交叉或变异后得到的新个体进行更新比较：如果更新后的方案更优，则继续迭代；否则增加第1阶段应急救援点的数量；

Step 7：检验第2阶段个体迭代达到稳定后，如果达到则转Step 8；否则，转Step 3；

Step 8：对第2阶段个体进行选择和变异操作。

3 算 例

某区域内有12个行政区域，各行政区域的路网如图1所示。在图1中，节点表示行政区域的灾害点或者救援点的配置中心。图的弧边的数据表示应急物资运输的单位运价（元/t）。该区域受到地震的影响，应急救援路网中断的路段：3-10、4-5、8-9、10-12、7-12、12-13。灾害点集合为{10、12、7、13、11}。

图1 应急救援路网Fig.1 Emergency rescue road network

在应急救援网络中节点的应急救援固定成本if、应急救援变动成本id，应急救援节点容量iC限制等如表1所示。G为灾害发生后应急配送成本的总额350万。灾害点的应急物资需求量可以根据该区域的人口数量、受灾程度进行估计，分别取2%，7%，12%的扰动为最大偏差ˆjβ（单位：t）。各灾害点的需求量下界为βj（单位：t）。相关的参数列表表示：表1分别为应急物资配置固定成本、可变成本及容量等参数；表2分别为灾区的需求量、扰动量及补偿价格等参数；表3分别为损毁路段及修复路段后收益等参数。

表1 各行政区应急物资配置的固定成本、可变成本及容量Tab.1 Fixed costs, variable costs and capacity of borough’s emergency supply configure

表2 灾区的需求量、扰动量及补偿价格Tab.2 Demand of disaster district, disturbance and compensation price

表3 道路修复后的救援收益Tab.3 Rescue income after road repair

通过 matlab采用算法对模型进行求解，当应急救援路网的需求是确定的，即：1Γ=2Γ=0时，求得最优目标值0Z为1733695元。当扰动为7%时、2Γ=2时的稳定性结果如表4所示。

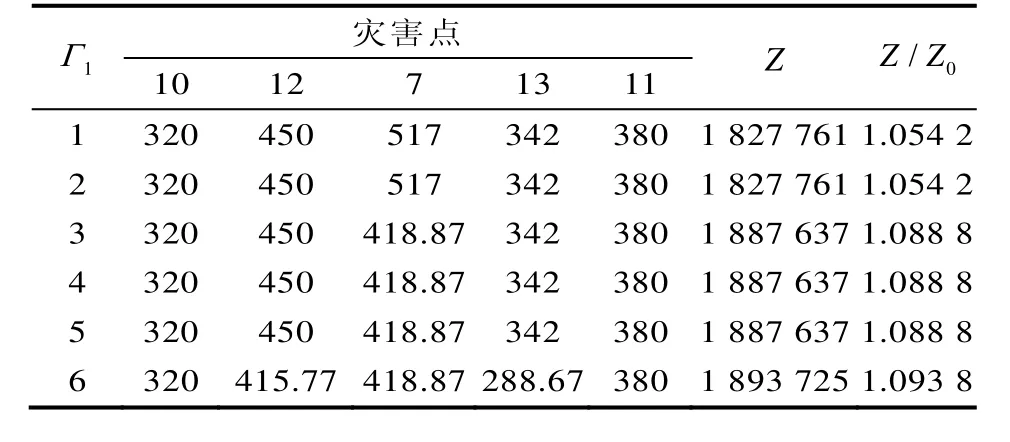
表4 稳定性方案（2Γ=2，扰动比例为7%）Tab.4 Stability program (2Γ=2, the disturbance ratio is 7%)

由表4可知，当1Γ=1、1Γ=2时，应急物资的调度不变，说明在应急救援路网中道路的损毁对应急调度没有影响。当1Γ=3、1Γ=4、1Γ=5时，应急物资的调度方案发生变化，应急调度方案需要进行调整。当1Γ=6，最优的应急调度方案发生变化，稳定性变化增大。所以，应急管理部门的决策者可以根据不同的风险偏好对1Γ、2Γ进行控制，进行决定最优的应急物资配置方案。如果要控制风险，当扰动变大时，则需要增加资金和物资的投入，以得到应急物资调度方案的稳定性。

由表5可知，当2Γ=2，2Γ=1或者2Γ=3或者1Γ=5或者1Γ=6时，0/ZZ随着扰动变化增大而增大，表示应急物资调度方案越不稳定。1Γ和2Γ变化越大，应急物资调度方案的稳定性就越差，方案的稳定性随着1Γ、2Γ变动增大而减弱。应急管理部门的决策者对应急需求不确定性所带来的风险偏好决定1Γ、2Γ的变化，进而确定应急物资的调度方案。当决策者需要增强应急救援方案稳定性，则需要增加应急救援方案的投资。

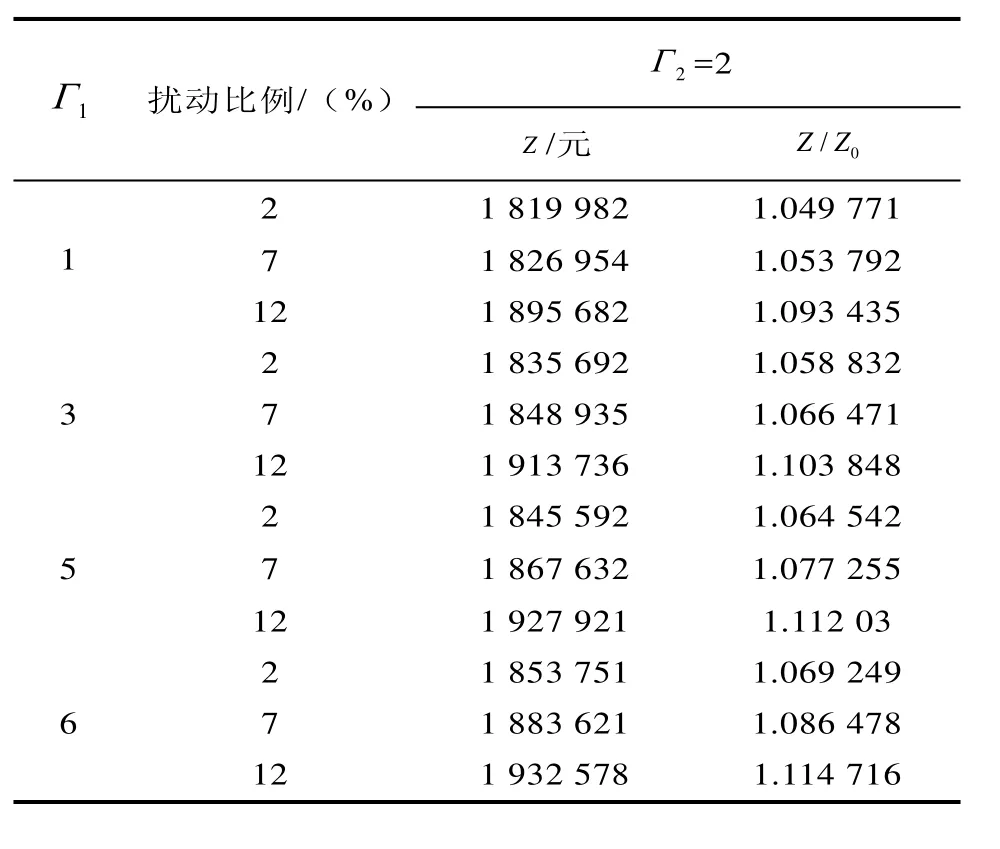
表5 不同稳定性及扰动比例结果Tab.5 Stability and the proportion of different disturbance results

4 结束语

本文将路网阻断、修复及需求不确定结合起来建立应急物资调度模型，然后采用启发式算法对模型进行求解。通过算例证明模型及算法的有效性，该研究同时为决策部门提供决策支持，根据决策者的不同风险偏好，选择路网的修复、资金和物资的投入，如果要控制风险，当扰动变大时，则需要增加资金和物资的投入，以得到应急物资调度方案的稳定性。在模型中进一步考虑灾害区的灾民满意度，决策部门的行为等约束条件是进一步研究的方向。

[1] 陈 森，姜 江，陈英武，等. 未定路网结构情况下应急物资车辆配送问题模型与应用[J]. 系统工程理论与实践，2011，31（5）：907-913.

[2] 王旭坪，马 超，阮俊虎. 运力受限的应急物资动态调度模型及算法[J]. 系统工程理论与实践，2013，33（6）：1493-1500.

[3] 陈钢铁，帅 斌. 震后道路抢修和应急物资配送优化调度研究[J]. 中国安全科学学报，2012，22（9）：166-171.

[4] 陈钢铁，帅 斌. 危险品事故泄漏模糊路网应急资源优化研究[J].中国安全科学学报，2012，22（3）：153-171.

[5] Ben-Tal Aharon，Nemirovski Arkadi. Robust optimization-methodology and applications [J].Mathematical Programming，2002，92（3）：453-480.[6] Ben-Tal Aharon，Ghaoui Laurent E. I., Nemirovski Arkadi. Robust optimization [M]. New Jersey:Princeton University Press，2009：1-542.

[7] Bertsimas Dimitris，Sim Melvyn. The price of robustness[J]. Operations Research，2004，52（1）：35-53.

[8] 张 玲，王 晶，黄 钧. 不确定需求下应急资源配置的鲁棒优化方法[J].系统科学与数学，2010，30（10）：1283-1292.

[9] 王雪峰，孙小明，郑柯威，等. 定位-车辆路径问题的两阶段混合启发式算法[J].上海交通大学学报，2006，40（9）：42-47.