一种基于云计算环境的动态车辆路径问题解决策略
宁 涛 陈 荣 郭 晨 冯瑞芳
1. 大连交通大学,软件学院,大连 116045
2. 大连海事大学,信息科学技术学院,大连 116026
0 引 言
车辆路径问题(Vehicle routing problem, VRP)[1]是运筹学领域的经典优化组合问题,它由Dantzig和Ramser于1959年提出,其解决思路是通过构造适当的车辆行驶路线来实现运输成本的最小化。VRP的研究历经50多年已被证明是典型的NP-Hard问题,具有较强的实际应用意义,并衍生出众多路径模型。动态车辆路径问题(Dynamic vehicle routing problem,DVRP)[2]于1988年被Psaraftis首次提出,之后的学者在信息更新、需求迫切程度等方面对DVRP开展了研究。Pureza对有时间窗的DVRP进行了研究,研究否定了按照新增加需求的顺序对车辆进行调度,提出了基于适当数量缓冲区的解决方案[3]。Mitrovic-Minic对快递公司邮件车辆等待时间进行了研究,并提出了基于实际数据的四种动态等待策略[4]。Haghani在分析了车辆配送过程需求动态变化的特点,提出了用遗传算法求解DVRP,并得出了实时交通信息与 DVRP动态变化成正比的关系[5]。Lchoua则分析了DVRP过程中出现动态事件的概率,在此基础上用模糊预定点生成动态调度方案[6]。Hanshar以报品配送为背景,用遗传算法求解DVRP并指出采用2-Exchange改进方法可以迅速求解问题[7]。Fattahi分析了选定的在线算法求解DVRP的竞争比率,提出了一种自适应局部粒子搜索策略可以将企业利益最大化,同时提出了对潜在客户的挖掘算法[8]。
基于上述研究方法,本文提出了基于云计算环境的改进遗传算法求解DVRP。文中首先建立面向不同约束条件的DVRP数学模型;针对动态调度的特点,提出双链遗传算法进行车辆分配链和路径优化链的编码方法;在云计算理论基础上,设计云交叉算子和云变异算子来改进遗传算法的交叉和变异操作,进而提出云计算环境下的自适应遗传算法(Cloud-based adaptive genetic algorithm, CAGA)求解DVRP调度问题,最后通过仿真实验和实例验证算法的有效性。
1 DVRP调度模型
1.1 问题描述
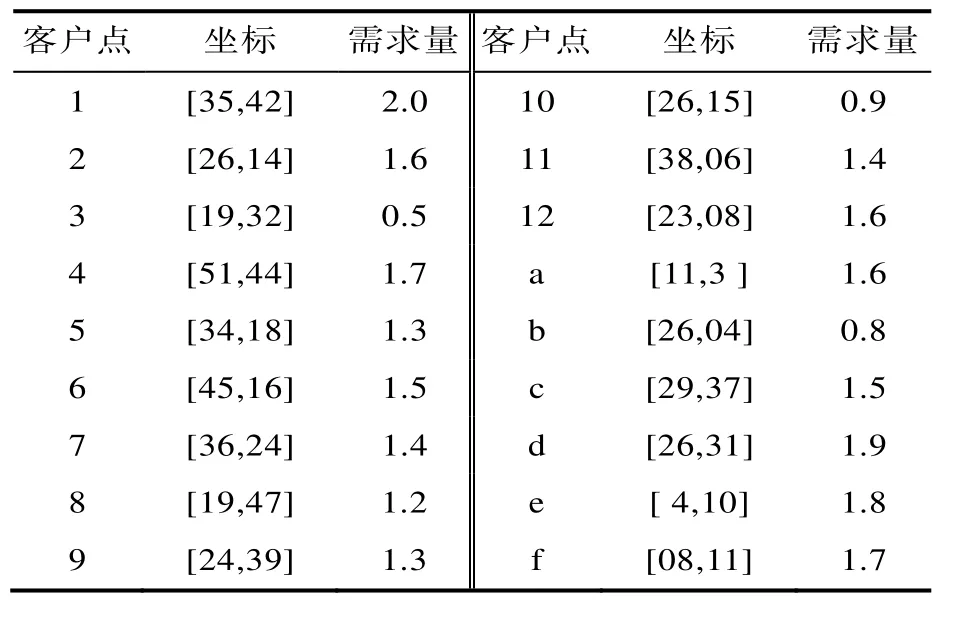
实际生活中,车辆路径问题存在大量的不确定性,客户需求、运输需求、路径制定者的主观认识、交通路况及车况等变化都需要调度管理员借助调度系统在短时间内对更新的信息作出快速正确的响应,并修改生成新的路径规划。具有动态需求的 DVRP可描述如下:某运输网络系统中存在 1个车场和 m个待服务的节点(客户点),表示为0,1,2,…,m,车辆从车场出发并对一定数量的客户提供配送服务后返回车场。根据需求的不同可将客户分为确定性客户和不确定性客户。当客户需求不变时,运输网络是静态车辆路径问题(Static vehicle routing problem,SVRP);当客户的需求发生改变时,调度系统修改已制定的路径计划,此时的运输网络是DVRP。已知每辆车的运输能力为C,每个节点需求量为模糊数D,节点i与节点j之间的距离为cij,求解满足运输需求费用最小的车辆行驶路线的目标是最小化运输车队数量以及最小化运输行驶距离。本文研究的 DVRP包括拥有一队同型号车辆的配送中心(配送车场)和待服务的客户集合,每个客户仅允许由一辆车配送服务一次。模型建立的符号表示为:配送车场编号为0;客户编号为 1,2,…,N;配送中心车辆编号为 1,2,…,K;i,j表示配送车场点以及客户点(i, j∈ { 1、2、…、N});车辆的最大载重量为Q;车辆k从客户点i出发的累积载量为qik,且qik 动态实时需求发生前,车辆已经对部分客户进行了配送服务。在车载量允许的情况下,将新的客户需求加入到已有路径中,若该需求无法导入已有路径,则需要增加新的车辆。如果原客户需求量增加,且超出最大车载量,则选择此子路径上最后配送服务的客户点作为新客户处理,直至满足车载量的限制。如果把该客户点看作配送车场,则原来的单配送路径问题就变换为多配送路径问题。假设 W为静态阶段尚未服务的客户需求与动态阶段新增加客户需求的总量;M 表示作为新配送车场的客户点数量,其编号为N+1、N+2、…、N+M,则原来的车场编号变为N+M+1,L表示新增加的车辆数。静态阶段从车场出发的车辆处在第i个客户位置,其编号为W+i;静态阶段车辆的剩余车载量为Q-qik。 定义决策变量: 建立 t时刻动态实时需求路径问题的数学模型如下: 式(1)表示目标函数,包括静态阶段未完成配送和动态阶段新增加用户的运输成本、动态阶段新增加车辆的运输成本以及动态阶段新派出车辆的发车成本。 式(2)表示每个客户都必须被配送服务的约束条件。 式(3)和式(4)表示每个客户只能被一辆车配送服务。 式(5)表示每台从车场出发的车辆都是满载状态。 式(6)表示车辆给任何客户配送服务前不能使空载状态。 本文在概率幅编码的基础上引入新的补偿因子γ(1γ≥),假设pi表示一条量子染色体,则第i个染色体编码方案如下: 式中,α、β满足α+β2=1;a=2π×δ,δ表示(0, ij 1)间的随机数, i = 1 ,2,… ,n ;j = 1 ,2,… ,m ; n表示种群规模,m表示量子位个数。补偿因子γ使周期由2π扩展为多周期以提高算法的收敛概率。每条染色体包含两个并列的基因链,每个基因链对应一个优化解,则每条染色体对应搜索空间的两个最优解,表示DVRP问题的车辆分配链和货物配送链,即: 式中,picos和pisin分别叫做余弦解和正弦解,当染色体进行迭代时,两个解可同步更新以扩大搜索空间,增加最优解数目。 在种群的进化过程中,假设两个父代个体的适应度分别表示为f1和f2,父代种群的最大适应度表示为Fmax,最小适应度表示为Fmin,则存在实数pcr满足: 式中,pc为云交叉算子;t1、t2和均为常数;=(f1+f2)2;y是关于Fmax和Fmin的一个正态随机数。 因为云交叉算子同时具有适应性和随机性的特点,所以,本文设计云交叉算子优化一般遗传算法的交叉操作,交叉算子的产生始终是以父代个体的平均适应度为基准而变化,但又随正态随机数y的变化而变化。云交叉算子的算法如下: 步骤 1:计算父代个体适应度的均值 Ex,记为 步骤2:以En为期望值,以He为标准差生成一个正态随机数 En′,其中 En=m1(Fmax-Fmin),He=n1En,m1和n1表示控制系数。 步骤 3:根据式(8)计算得到云交叉算子 适应度的平均值,f = max(f1, f2)。 在种群进化过程中,假设单个父代个体的适应度表示为f1,则存在实数pmt满足: 式中,pm为云变异算子。式(9)中 s1、s2和F均为常数,Fmax、Fmin和y的概念同式(8)。 云变异算子的稳定倾向性由f1、Fmax和Fmin三个参数所决定,本文设计云变异算子优化一般遗传算法的变异操作,云变异算子的算法如下: 步骤1:设单个父代个体适应度的均值Ex,记为 步骤2:以En为期望值,以He为标准差生成一个正态随机数 En′;其中 En=m2(Fmax-Fmin),He=n2En,m2和n2表示控制系数。 本文设计的基于云模型理论自适应遗传算法的关键是用云交叉算作、云变异算子和云发生器对遗传算法的交叉和变异算子进行改进以提高算法的收敛速度和改善解搜索的效果。 云自适应交叉概率和云自适应变异概率如图 1所示: 图1 云自适应交叉概率pc和变异概率pmFig.1 Cloud adaptive crossover probability pc and mutation probability pm 云自适应遗传算法的步骤为: 步骤1:随机产生n个个体组成初始种群,进行双链量子编码,并初始化pc和pm; 步骤 2:设计表达式为f′(x) = 1 /Z(x)的适应度评价函数,Z(x)表示个体目标函数值,函数值越小个体越优秀; 步骤3:利用最佳个体保留策略和适应度比例选择进行种群个体选择,以确定进入下一代种群个体的范围; 步骤 4:根据式(8)利用云发生器生成交叉算子pc,并对父代个体进行交叉操作; 步骤 5:根据式(9)利用云发生器生成变异算子pm,并对个体进行互换变异操作; 步骤6:通过选取父代种群的m个优秀个体和子代种群的相应个体组合后重新构建新种群,从而扩大种群规模并增加搜索空间; 步骤7:判断是否满足停止条件,若没满足跳至步骤3;否则停止算法运行。 为了对本文提出方法的有效性进行验证,设计了包括 1个车场、6个动态需求(新增)客户点和 12个静态需求客户点的模型。设车辆行驶区域为60×60(单位:km)的近似正方形。静态客户编号为1,2,3,…,12,新增客户编号为 a、b、c、d、e、f。约定每个客户点的配送最大量不超过2 m3,配送车辆的最大载货量都是16 m3,车辆连续行驶的最长距离为300 km,同时设配送车场坐标为(25 km,25 km),动态和静态客户点信息如表1所示,其中动态需求出现于“时刻1”。 表1 客户信息Tab.1 Information of customers 初始配?送车辆数m示第i个客户点的需求量;Q表示车辆最大载货量;α表示货物装厢的复杂度,取值为 0.6;m取值为整数。在初始时刻车辆对12个静态客户点进行配送服务,调度方案如图2所示, 图中0表示出发车场,车辆1配送客户点为 1-2-3-4-5,车辆 2配送客户点为6-7-8-9- 10-11-12;而当时刻1新增客户需求点a、b、c、d、e和f后,利用本文提出的调度策略进行重调度。按照初始调度计划派出的2台车分别位于客户点4和9,即动态因子关键点集合为{4,9},此时车辆从这两个关键点出发的载货量集合为{5.8,5.4},利用CAGA对问题进行求解,生成时刻1的重调度方案如图3所示。在时刻1配送车辆的路径和载货率情况如表2所示。 重调度计划表中的载货率等数据表明本文提出的基于云计算环境的CAGA及其调度策略是有效的。为进一步验证所提出方法的性能,将 CAGA与已经存在的 AIA[9]、CQPSO[10]、PSO+TS[11]和 MADSA[12]算法应用于同一问题的求解。由图 4可知,本文提出的CAGA和AIA算法在执行100次运算获得的目标值最小,即算法稳定性最高, 同时使用CAGA算法求解DVRP问题时,可以最小化总配送距离、节省配送时间,能够使载货率最大化。 图2 初始调度方案Fig.2 Initial scheduling 图4 不同算法的稳定性目标值比较Fig.4 Objective comparison among different algorithms 图3 时刻1重调度方案Fig.3 Rescheduling at moment 1 表2 时刻1重调度计划Tab.2 Rescheduling at moment 1 本文面向不同约束条件,建立了多目标 DVRP数学模型,提出了基于双链量子进行编码的方法;设计云交叉算子和云变异算子对一般遗传算法的交叉和变异操作进行改进;进而提出了基于云计算理论的自适应遗传算法求解DVRP问题。为验证算法的有效性,将上述算法应用仿真算例,结果表明:与其他优化算法相比,本文算法在求解多目标调度问题时具有收敛速度快、求解质量高的优点。在本文研究结果的基础上,进一步的研究应着重于考虑基于云计算的车辆调度过程中对配送时间点增加提前和拖后惩罚系数。 [1] Dantzig G. and Ramser J. The truck dispatching problem[J]. Management Science, 1959, (6): 80-9 1.[2] Psaraftis H. N. Dynamic vehicle routing problem[M].In: Golden B L, Assad A A, eds. Vehicle routing:methods and studies. Amstersam, North-Holland:Elsevier Science Ltd, 1988: 223-248. [3] Pureza V., Laporte G. Waiting and buffering strategies for the dynamic pickup and delivery problem with time windows[J]. Infor: Information System and Operational Research, 2008, 46(3): 165-175. [4] Mitrovic-Mini S., Laporte G. Waiting strategies for the dynamic pickup and delivery problem with time windows [J]. Transportation Research Part-B-Method Logical, 2004, 38(7): 635-655. [5] Haghani A., Jung S. A dynamic vehicle routing problem with time-dependent travel times [J].Computers & Operations Research, 2005, 32(11):2959-2986. [6] Choua S., Gendreau M., Potvin J. Y. Exploiting knowledge about future demands for real-time vehicle dispatching [J]. Transportation Science, 2006,40(2): 211-225. [7] Hanshar F. T., Ombuki-Berman B. M. Dynamic vehicle routing using genetic algorithms[J]. Applied Intelligence, 2007, 27(1): 89-99. [8] Fattahi P., Fallahi A. Dynamic scheduling in flexible job shop systems by considering simultaneously efficiency and stability [J]. CIRP Journal of Manufacturing Science and Technology, 2010, 2(2):114-123. [9] Bagheri A., Zandith M., Mahdavi I., Yanzdanni M.An artificial immune algorithm for the flexible jobshop scheduling problem[J]. Fut Gen Comp Sys,2010, 26(4): 533-541. [10] 汤健超. 基于混合进化算法的若干调度问题研究[D]. 广州:华南理工大学, 2012. [11] 宁 涛. 混合量子算法在车辆路径问题中应用的研究[D]. 大连:大连海事大学, 2013. [12] Seyed Habib A., Rahmat M., Zandieh M. Yazdani.Developing two multi-objective evolutionary algorithms for the multi-objective flexible job shop scheduling problem [J]. The International Journal of Advanced Manufacturing Technology, 2013, 64(5):915-932.1.2 目标函数






2 基于云计算理论的自适应遗传算法
2.1 双链遗传算法编码


2.2 云交叉算子

2.3 云变异算子
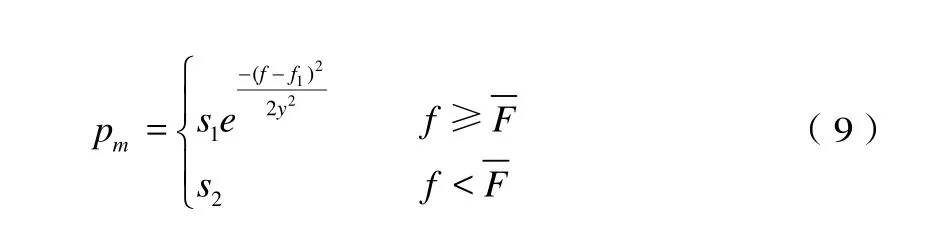

2.4 云自适应遗传算法设计
3 数据分析与验证



4 结束语


