导线标准冰厚的直径订正系数试验研究

杨加伦，朱宽军，尹泉，刘彬，李新民，司佳钧

(中国电力科学研究院，北京市 100192)



导线标准冰厚的直径订正系数试验研究

杨加伦，朱宽军，尹泉，刘彬，李新民，司佳钧

(中国电力科学研究院，北京市 100192)

架空输电线路导线覆冰可能导致电网系统发生机械或电气故障，因此，确定导线设计冰厚对电网的安全稳定运行具有十分重要的作用。确定架空输电线路导线设计冰厚时，需要通过线径订正公式将不同导线直径上的标准冰厚折算至设计导线上。通过人工气候室内覆冰试验获取相关覆冰数据，针对不同覆冰类型分别拟合了导线的直径订正系数。结果显示：雾凇和混合凇的导线直径订正系数随着线径的增加而减小，且雾凇减小的趋势较混合凇明显；雨凇的导线直径订正系数随着线径的增加而增加。

导线；标准冰厚；直径订正系数；人工气候室

0 引 言

架空输电线路导线覆冰可能导致电网系统发生机械或电气故障，轻则引起闪络跳闸，重则导致金具损坏、断线甚至倒塔等，对生产与生活造成严重影响[1-6]。科学合理地确定架空输电线路导线设计冰厚既可以保证电网抵御覆冰灾害的能力，又可以调整电网工程的整体造价。因此，研究影响导线设计冰厚的各种因素，如高度订正系数、重现期换算系数和线径订正系数等引起了国内外学者和工程技术人员的浓厚兴趣。通常情况下，确定输电线路设计冰厚需要获取大量的历史覆冰资料[7-10]。气象部门和电力部门是导线覆冰相关数据的重要来源。例如，2011年之前，我国气象部门有280余个站点开展直径为4 mm导线的覆冰观测业务。为了配合电力部门的需求，自2011年1月1日起，全国共有857个气象观测站利用安装有直径为26.8 mm导线的新式积冰架开展覆冰观测业务。电力部门在架空输电线路设计、建设、运行和维护过程中会收集到大量的覆冰资料，包括不同直径导线的覆冰数据。可见，有必要将收集到的不同直径导线上的覆冰厚度折算到设计导线的覆冰厚度，再进行特定重现期设计冰厚的计算，为架空输电线路的设计提供参考。

国内外的相关技术规程，如国际电工委员会编制的标准IEC 60826《Design criteria of overhead transmission lines》、捷克斯洛伐克输电线路规程与我国电力行业标准DL/T 5158—2012《电力工程气象勘测技术规程》等[11-13]推荐了覆冰的导线直径订正公式。但是，国内外就覆冰标准冰厚的直径订正公式并未形成统一认识。因此，针对不同覆冰种类进行深入研究具有十分重要的现实意义。

本文针对导线标准冰厚的直径订正公式及订正系数，在人工气候室内开展6种真型导线的覆冰试验，探索标准冰厚受导线直径影响的规律。

1 导线覆冰试验

为克服自然环境下覆冰数据稀缺的问题，在人工气候室内开展了真型导线覆冰试验。人工气候室内部的风口阵列和导线布置方式如图1所示。6种导线直径分别为11.4，21.6，26.8，33.8，39.9，47.0 mm，为便于叙述依次称为1～6号导线。开展了13种工况的覆冰试验，包括4种混合凇工况、5种雾凇工况和4种雨凇工况，采集覆冰数据共计1 704组。图2是试验采集的部分覆冰图片。表1是温度为-6 ℃、风速为1 m/s时混合凇覆冰的质量数据。

图1 风口阵列及导线布置方式Fig.1 Air outlet pattern and layout of conductors

图2 人工气候室内导线覆冰类型Fig.2 Icing types on conductors in artificial climate chamber表1 温度为-6 ℃、风速为1 m/s时导线混合凇覆冰的质量Table 1 Weight of mixed-phase icing on conductors (Temperature:-6℃, Wind speed: 1 m/s)

利用下式将试验获取的全部覆冰质量数据转换为特定导线直径上的标准冰厚数据[13]。

(1)

式中:b0是标准冰厚，mm；r为导线半径，mm；L为覆冰体长度，m；G为冰重，g。由于式(1)未涉及覆冰的密度，因此雨凇、雾凇和混合凇覆冰的质量均可由式(1)转换为标准冰厚。

图3为某一工况下雾凇、混合凇和雨凇覆冰的标准冰厚与导线线径的关系。可知，雾凇和混合凇的标准冰厚随着导线直径的增长而减小；雨凇的标准冰厚随着导线直径的变化趋势并不明显，基本随着导线直径的增加而增加。可见，导线直径对覆冰荷载的影响程度与覆冰类型有关。因此，我们将针对不同的覆冰种类，分别研究线径订正公式。

图3 不同覆冰类型标准冰厚与线径的关系Fig.3 Relationships between standard ice thickness and diameter of conductors for different icings

2 导线标准冰厚直径订正系数拟合

2.1 常用的导线直径订正公式

目前常用的覆冰线径订正公式有2种形式，分别为对数形式和线性形式。其中，国际电工委员会编制的标准IEC 60826《Design criteria of overhead transmission lines》推荐的线径订正系数的计算公式如下[11]：

降水覆冰为

K1=0.35d/30+0.65

(2)

云中覆冰为

K2=0.15d/30+0.85

(3)

式(2)～(3)中d为导线直径，mm。

需要指出的是，式(2)～(3)是覆冰质量的线径订正公式，不是标准冰厚的线径订正公式。国内确定输电线路设计冰厚，如果应用上式需进行复杂的换算，不适用于订正标准冰厚相对于线径的变化。

我国电力行业标准DL/T 5158—2012《电力工程气象勘测技术规程》针对无实测资料地区推荐的线径订正公式如下[13]：

(4)

式中：φ是设计导线直径，mm，φ≤40 mm；φ0是覆冰导线直径，mm。

巢亚锋等[14]根据三峡地区的实测覆冰数据得出了导线线径订正公式如下：

(5)

2.2 基于对数形式的线径订正系数拟合

麦夸特法是一种利用梯度求最大(小)值的算法，同时具有梯度法和牛顿法的优点[15]。因此，本文利用麦夸特法拟合上述2种形式的线径订正公式。

综合考虑式(4)和(5)，假设对数订正公式如下：

(6)

式中：a为待定系数；φ0为基准导线直径，取26.8 mm；φ为设计导线直径，分别取21.6，26.8，33.8，39.9及47.0 mm；Kφ为线径订正系数，是设计导线和基准导线在同等气象条件下标准冰厚的比值。

表2列出了不同覆冰类型的对数订正结果，包括利用麦夸特法拟合的系数a和均方误差。全部覆冰对应的结果是指包含雨凇、雾凇和混合凇在内的1 704组全部覆冰数据的对数订正公式的拟合结果。

表2 对数订正公式的拟合结果

Table 2 Fitting results of logarithmic correction formula

2.3 基于线性形式的线径订正公式拟合

考虑式(2)～(3)，假设线性形式的线径订正公式如下：

Kd=ad/d0+b

(7)

式中：a和b为待定系数；d0为基准导线直径，取26.8 mm；d为导线设计直径，分别取11.4，21.6，26.8，33.8，39.9，47.0 mm；Kd为线径订正系数。

与处理对数形式的线径订正公式类似，为比较不同类型的线性形式的线径订正结果，分别针对混合凇、雾凇和雨凇覆冰数据以及全部1 704组覆冰数据，利用麦夸特法拟合系数a和b，并计算均方误差，具体结果见表3。

表3 线性订正公式的拟合结果

Table 3 Fitting results of linear correction formula

3 结果分析

由表2～3可知，2种订正公式针对同一种覆冰的均方误差差别不是很大。另外，混合凇、雾凇的均方误差要小于雨凇的均方误差，雨凇的均方误差约为混合凇和雾凇均方误差的3倍。因此，为了提高雨凇覆冰的拟合精度、降低拟合结果的均方误差，应该考虑引入其他形式的公式。

图4～6分别为混合凇、雾凇和雨凇的线径订正系数曲线。需要指出的是，图中对数和线性订正公式曲线反应的是根据4次混合凇覆冰试验数据、5次雾凇覆冰试验数据和4次雨凇覆冰试验数据分别统计的拟合结果。个别试验数据由于覆冰质量测量误差或者导线直径测量误差等可能与上述统计结果反映的总体趋势不一致。

图4 混合凇的各种线径订正公式曲线Fig.4 Curves of diameter correction coefficient for mixed-phase icing

由图4可知，根据电力行业标准公式、巢亚锋公式、对数公式和线性公式计算的线径订正系数走向基本一致。在30 mm及以上范围内，对数订正公式与电力行业标准公式和巢亚锋公式的计算结果较为接近；在25 mm及以下范围内，线性订正公式与电力行业标准公式和巢亚锋公式的较为接近。

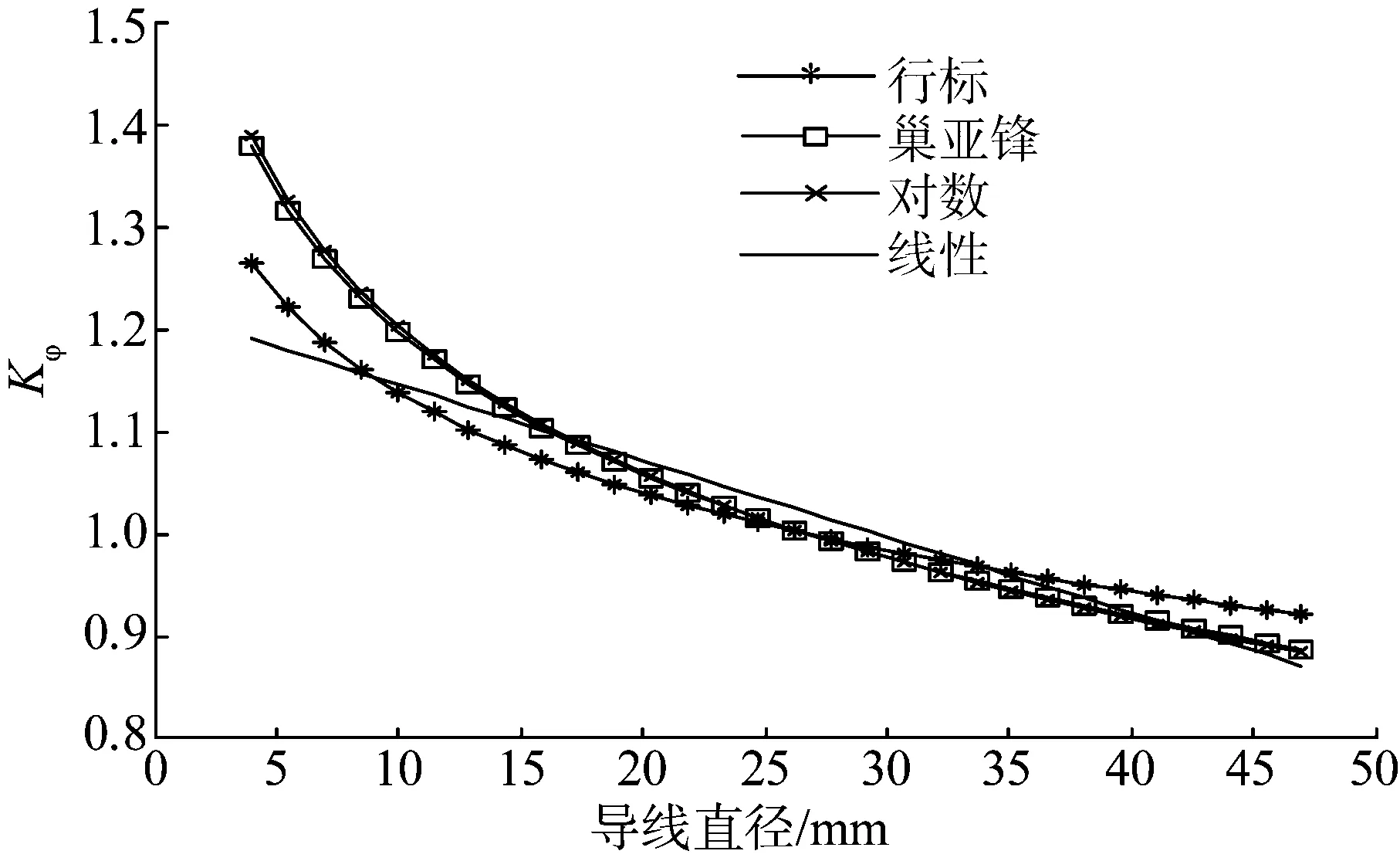
图5 雾凇的各种线径订正公式曲线Fig.5 Curves of diameter correction coefficient for rime

由图5可知，对于雾凇的线径订正系数，电力行业标准公式、巢亚锋公式、对数公式和线性公式的走向基本一致。对数订正公式与巢亚锋公式的计算数据非常接近。线性订正公式在8 mm附近和33 mm附近的计算数据与电力行业标准的较为接近。

图6 雨凇的各种线径订正公式曲线Fig.6 Curves of diameter correction coefficient for glaze icing

由图6可知，对于雨凇的线径订正系数，对数公式和线性公式的计算结果与电力行业标准公式和巢亚锋公式的走向不一致，即随着线径的增加，雨凇标准冰厚也逐渐增加。由于雨凇对输电线路造成的误差较雾凇和混合凇更为严重，需要引起相关工程技术人员的重视。

综上所述，不同类型覆冰受线径大小的影响规律不同。其中，混合凇和雾凇的标准冰厚随着线径的增长而减小，而雨凇的标准冰厚随着线径的增长而增长。

4 结 论

(1)获取了6种真型导线在人工气候室内13种工况下1 704组覆冰数据。通过比对发现，应该针对不同覆冰类型拟合导线标准冰厚的直径订正系数。

(2)基于人工气候室获取的覆冰数据可知，雾凇和混合凇的导线直径订正系数随着线径的增加而减小，且雾凇减小的趋势较混合凇明显。雨凇的导线直径订正系数随着线径的增加而增加。

[1]McKey G A, Thompson H A.Estimating the hazard of ice accretion in Canada from climatological data[J].Journal of Applied Meteorology, 1969, 8(4): 927-935.

[2]韩军科, 杨靖波, 杨风利.500 kV酒杯塔覆冰破坏形态分析[J].电力建设, 2009,30(11): 21-23.Han Junke,Yang Jingbo,Yang Fengli.Analysis of failure mode on iced 500 kV transmission cup-type tower[J].Electric Power Construction,2009,30(11):21-23.

[3]任永健，周月华，肖莺, 等.无气象观测地区的电线覆冰厚度推算[J].气象科学, 2011, 31(3): 313-317.RenYongjian,ZhouYuehu,Xiao Ying, et al.The method of calculating the ice thickness on wire in the areas without meteorological observation[J].ScientiaMeteorologicaSinica,2011,31(3):313-317.

[4]胡毅.电网大面积冰灾分析及对策探讨[J].高电压技术，2008,34(2):215-219.Hu Yi.Analysis and countermeasures discussion for large area icing accident on power grid[J].High Voltage Engineering,2008,34(2):215-219.

[5]彭超贤, 刘长征.云南巧家“哨口子”送电线路覆冰倒杆事故分析[J].电力建设, 2008, 29(1):36-38.Peng Chaoxian, Liu Changzheng.Accident analysis of icing-caused transmission pole collapse in Shaokouzi, Qiaojia county, Yunnan Province[J].Electric Power Construction, 2008,29(1):36-38.

[6]肖智宏，刘学军，李显鑫，等.对架空输电线路设计企业标准的解读[J].电力经济技术, 2009, 21(5), 40-45.Xiao Zhihong, Liu Xuejun, Li Xianxin, et al.Techno-economic analysis on SGCC technical code for overhead transmission line design[J].Electric Power Technologic Economics,2009,21(5):40-45.

[7]陆佳政, 张红先, 彭继文, 等.基于极值Ⅰ型概率分布模型的湖南地区电网覆冰重现期计算[J].高电压技术, 2012, 38(2): 464-468.

Lu Jiazheng, Zhang Hongxian, Peng Jiwen, et al.Calculation of Hunan power grid icing recurrence interval based on extreme-value type I probability distribution model[J].High Voltage Engineering, 2012, 38(2):464-468.

[8]杨加伦, 朱宽军, 刘彬, 等.输电线路冰区分布图绘制关键技术[J].电力建设, 1995，16(11)：56-61.Yang Jialun, Zhu Kuanjun, Liu Bin, et al.Technologies of icing distribution map for power transmission line[J].Electric Power Construction,2013,34(9):31-36.

[9]邹明华，邓洪洲.输电线路设计覆冰厚度统计模型取用[J].电网与清洁能源, 2010, 26(1): 40-44.Zou Minghua, Deng Hongzhou.Study on probability distribution model of designed ice load for transmission lines[J].Power System and Clean Energy, 2010,26(1):40-44.

[10]Sundin E, Makkonen L.Ice loads on a lattice tower estimated by weather station data[J].Journal of applied meteorology, 1998, 37(5): 523-529.

[11]IEC 60826—2003 Design criteria of overhead transmission lines[S].Geneva, Swilzerland: International Electrotechnical Commission, 2003.

[13]DL/T 5158—2012电力工程气象勘测技术规程[S].北京：中国计划出版社, 2012.

[14]巢亚锋， 蒋兴良，毕茂强,等.导线覆冰厚度的直径订正系数[J].高电压技术，2011，37(6)：1391-1397.Chao Yafeng, Jiang Xingliang, Bi Maoqiang, et al.Diameter Correction coefficient of the icing thickness on the conductors[J].High Voltage Engineering, 37(6):1391-1397.

[15]Madsen K, Nielsen H B, Tingleff O.Methods for non-linear least squares problems, Informatics and Mathematical Modelling[M].Denmark: Technical University of Denmark, 2004: 24-29.

(编辑：张小飞)

Experimental Study on Diameter Correction Coefficient of Standard Ice Thickness on Conductors

YANG Jialun, ZHU Kuanjun, YIN Quan, LIU Bin, LI Xinmin, SI Jiajun

(China Electric Power Research Institute, Beijing 100192, China)

Accreted ice on conductors in transmission lines may cause mechanical and electrical faults to power grid system, leading to the fact that the determination of designed ice thickness on conductors plays an important role for the safe operation of power grid.When determining the designed ice thickness of conductors in transmission lines, the standard ice thickness on different diameters should be computed to the specific diameter with using diameter correction formula.Related ice data was acquired through experiments in artificial climate chamber, and the diameter correction coefficients of conductors were fitted respectively according to different types of accreted ice.The results show that the conductor diameter correction coefficients of rime and mixed-phase icing decrease with the increase of conductor diameter, and the decreasing trend of the correction coefficient of rime is larger than that of mixed-phase icing; the conductor diameter correction coefficients of glaze icing increases with the increase of conductor diameter.

conductor; standard ice thickness; diameter correction coefficient; artificial climate chamber

国家自然科学基金(51305411，51008288)；国家电网公司科技项目(GCB17201400162)。

TM 726

A

1000-7229(2015)03-0033-05

10.3969/j.issn.1000-7229.2015.03.006

2014-09-02

2014-12-25

杨加伦(1981)，男，高级工程师，主要研究方向为架空输电线路覆冰及振动问题；

朱宽军(1969)，男，高级工程师，主要研究方向为输变电工程力学，重点从事架空导线振动、舞动及覆冰等问题的研究；

尹泉(1985)，男，工程师，主要研究方向为架空输电线路覆冰及振动问题;

刘彬(1978)，男，高级工程师，主要研究方向为架空输电线路振动、舞动问题；

李新民(1974)，男，高级工程师，主要研究方向为架空输电线路振动、舞动问题；

司佳钧(1983)，男，工程师，主要研究方向为架空输电线路振动、舞动问题。

Project Supported by National Natural Science Foundation of China (51305411，51008288).