基于改进蝙蝠算法的配电网分布式电源规划

范彬，周力行，黄頔，刘家郡，刘博伟，朱凌峰

(长沙理工大学电气与信息工程学院，长沙市 410114)



基于改进蝙蝠算法的配电网分布式电源规划

范彬，周力行，黄頔，刘家郡，刘博伟，朱凌峰

(长沙理工大学电气与信息工程学院，长沙市 410114)

合理规划接入电网的分布式电源能够提高能源利用效率，提高电力系统运行的经济性、灵活性和可靠性。建立了以分布式电源建设和运行总费用最小、系统网损最小、静态电压稳定指标最大为优化子目标的多目标规划模型。采用了一种新的仿生算法——蝙蝠算法，并针对蝙蝠算法的不足之处进行了改进，有效地解决了该算法易陷入局部最优、后期收敛速度慢等问题。通过14节点配电网测试系统进行了分布式电源选址和定容仿真分析。仿真结果表明，与传统的蝙蝠算法、粒子群算法相比，采用改进的蝙蝠算法能够更好、更快地得到分布式电源接入配电网的最优规划方案，验证了算法的正确性和可行性。

分布式发电；蝙蝠算法；多目标优化；配电网；优化选址

0 引 言

分布式发电和大电网结合是电力系统的发展趋势之一，二者可以相互取长补短。分布式发电具有污染小、发电方式灵活、投资省以及提高电能质量等优点[1]。研究表明，当分布式电源接入电网后，会对电网产生很大的影响，包括电压水平、网损、可靠性、灵活性等方面，其影响的大小与分布式电源的安装位置和容量直接相关[2-4]。甚至不合理的分布式电源接入会使得电网的安全稳定运行受到严重威胁。因此，对分布式电源的选址和定容研究就显得尤为关键。

近年来，对分布式电源选址和定容的研究已经成为了国内外研究的热点。文献[5]运用改进的自适应遗传算法进行了配电网分布式电源规划，但是由于遗传算法本身存在收敛速度慢，易陷入局部最优解的缺陷，因此很难得到全局最优方案。文献[6]运用了机会约束规划建立以独立发电商收益最大为目标函数的风电接入配电网的选址和定容模型。文献[7]以配电网年运行费用最小为目标函数，采用粒子群优化(particle swarm optimization，PSO)算法对分布式电源的选址和定容进行了优化，但是目标函数仅仅只考虑了经济方面的影响，没有对电压质量和网损等方面进行综合考虑。文献[8]综合考虑了网损、电压质量和电流质量的影响，采用Grefenstette编码的遗传算法优化了分布式电源的选址和定容。

基于以上的不足，本文采用一种新的仿生算法——蝙蝠算法。建立以分布式电源建设和运行总费用最小、系统有功网损最小、静态电压稳定指标最大为优化子目标的多目标规划模型，采用改进的蝙蝠算法对14节点配电网测试系统进行分布式电源选址和定容，以及多个方案的比较，验证了该算法的正确性和可行性。

1 含分布式电源的多目标模糊规划模型

1.1 目标函数

本文综合考虑多个方面的因素建立目标规划模型，其中目标函数包括分布式电源的建设和运行总费用、系统网损和静态电压稳定指标这3个优化子目标[12]。

(1)分布式电源的建设和运行总费用函数为

(1)

式中：Tmax是分布式电源的最大发电小时数；m为配电网中的分布式电源总个数；SDGi为第i个分布式电源额定容量；CeDGi为第i个分布式电源的单位电量成本；ηi为第i个分布式电源的功率因数；CDG1i为第i个分布式电源的安装成本；CDG2i为第i个分布式电源的运行维护费用成本；CDG3i为第i个分布式电源的发电燃料费用成本。

(2)系统网损函数为

(2)

式中PLossi为第i条支路的有功网损。

(3)静态电压稳定指标函数为

f3=max(L1,L2,……,LNb)

(3)

式中：Nb是系统的支路数；Lj(j=1,2,…,Nb)表示第j条支路的静态电压稳定指标，其表达式为

(4)

式中：Rj和Xj分别为支路j的电阻和电抗；Pj和Qj分别为支路j的有功和无功；Vi为首节点的电压幅值。

1.2 隶属度函数

由于上述3个子目标函数的量纲是不同的，为了合理地协调这些目标函数之间的关系，采用了线性分段函数的方式，分别表示各子目标的模糊隶属度函数。

(5)

(6)

(7)

式中：μc、μp、μl分别为分布式电源的建设与运行总费用、系统网损和电压稳定指标这3个优化子目标的隶属度；C*、Cmax为函数f1单独进行优化时的最优和最大值；P*、Pmax为函数f2单独进行优化时的最优和最大值；L*、Lmax为函数f3单独进行优化时的最优和最大值。

通过上述处理，采用权重系数法就可以将原来的多目标规划问题转化为单一规划问题，即

μ=aμc+bμp+cμl

(8)

式中：a、b、c分别为μc、μp、μl的权重系数，μ表示综合隶属度，综合隶属度越大，表示算法优化结果越好。

1.3 潮流计算约束条件

潮流计算约束条件包括等式和不等式约束条件，其中，等式约束条件为有功功率平衡方程

(9)

式中：PDGi为节点i的分布式电源有功；PGi为节点i处发电机发出的有功；PL为有功网损；PD为系统有功负荷。

不等式约束条件包括：节点电压上下限约束

|Vi|min≤Vi≤|Vi|max

(10)

支路电流约束

|Ii|≤|Ii|max

(11)

分布式电源容量约束

(12)

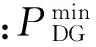
2 蝙蝠算法及其改进

2.1 基本蝙蝠算法

蝙蝠算法(bat algorithm，BA)是模拟自然界中蝙蝠通过回声定位方式来捕食猎物的生物特性，在2010年由Yang X S提出的一种新的智能优化算法。自该算法提出以来，已经有学者将其应用于优化问题，但是在电力系统优化问题上还很少有应用。已经有结果表明：相比较于粒子群算法、遗传算法与和声算法，蝙蝠算法具有发挥更大作用的潜力[13-14]。但基本蝙蝠算法与文献[5]中提到的遗传算法一样，也存在易陷入局部最优、发生过早收敛、后期收敛速度慢等问题[15]。本文针对基本蝙蝠算法的不足之处，对其加以改进，将改进的蝙蝠算法(improved bat algorithm，IBA)应用于配电网分布式电源规划。

基本蝙蝠算法的流程为：

(1)初始化基本参数。

(2)初始化蝙蝠群体的空间位置xi和速度vi。

(3)初始化脉冲频率fi、脉冲频度ri和脉冲音强Ai。更新蝙蝠的空间位置xi和速度vi。

(4)若任意数大于ri，则从处在最佳位置的蝙蝠群体中选择1个，对该蝙蝠进行随机扰动，用扰动后的位置取代蝙蝠i当前的位置。

(5)若任意数小于Ai，并且更新位置后蝙蝠i优于当前最佳蝙蝠的位置，则增大脉冲频度ri，减小脉冲音强Ai。

(6)根据移动后蝙蝠所处的位置，找出当前最佳蝙蝠。

(7)判断迭代次数或者搜索精度是否满足终止的条件，若满足则进行(8)，否则跳转到(3)。

(8)输出全局最优解[9,16]。

2.2 改进蝙蝠算法

针对基本蝙蝠算法容易陷入局部最优、发生过早收敛、后期收敛速度慢等问题。本文引入惯性权重系数ω对其进行改进。惯性权重系数ω能够让蝙蝠保持运动惯性，使其有扩展搜索空间的趋势，有能力探索新的区域。当ω较大时，蝙蝠能够扩展搜索空间，搜索以前所没有到达的区域，从而提高BA算法的全局搜索能力。当ω较小时，蝙蝠主要是在当前解附近搜索，局部搜索能力较强，收敛速度快。本文中按照式(13)来对ω进行调整，让ω随算法迭代的进行而逐渐减小，从而改善算法的收敛性能。设ωstart、ωend分别为惯性系数的起始值和终止值，t为当前迭代次数，tmax为最大迭代次数，c为惯性权重相关系数。则惯性权重系数、蝙蝠速度更新公式为

(13)

(14)

同时，通过对基本蝙蝠算法的仿真分析与调试，发现若对上述(5)中的判定条件：更新位置后的蝙蝠i优于当前最佳蝙蝠的位置改为优于蝙蝠i的当前最佳位置，这样不仅能够提高蝙蝠的移动能力，而且能够使算法收敛得更快，结果更优。

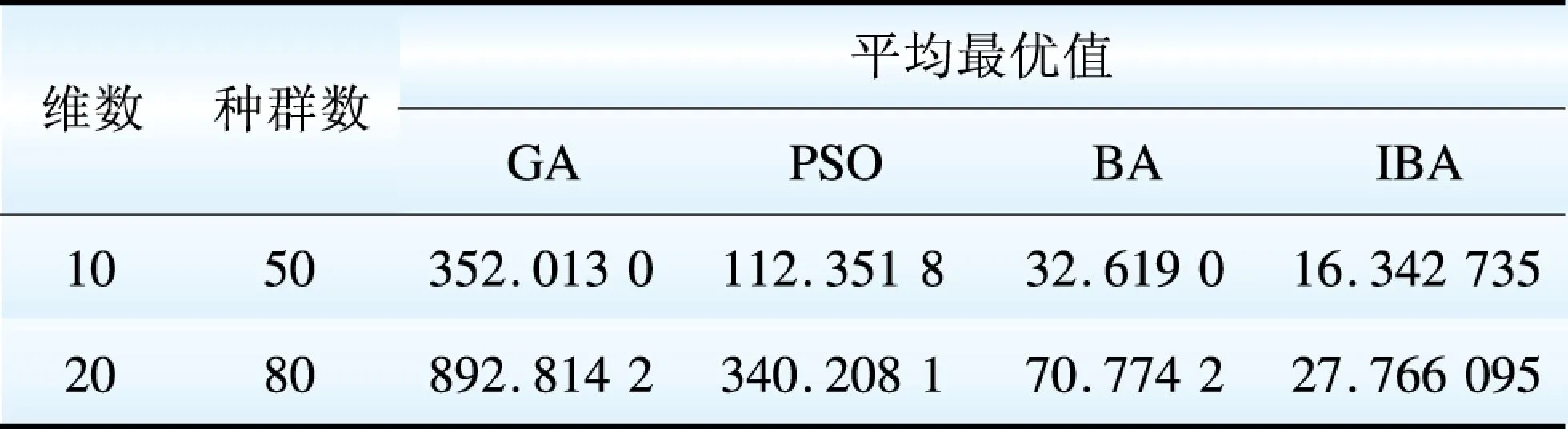
本文选取Rosenbrock测试函数来进行仿真测试。图1为二维Rosenbrock测试函数下，更改判定条件前后蝙蝠i的寻优移动情况仿真结果，由图1可以看出，更改后蝙蝠i的移动能力明显强于更改前，这有利于算法更快更好地找到最优解。如图2、表1所示，按照文献[16]中BA算法的参数设置，将IBA算法的仿真结果与文献[16]中遗传算法(genetic algorithm，GA)、粒子群算法、蝙蝠算法的测试结果进行比较，发现改进的蝙蝠算法具有更快的收敛速度，并且能够得到更优的计算结果。

Rosenbrock测试函数为

(15)

式中：D表示维数；xi∈[-2.048, 2.048]，理论最优值为f(1,…,1)=0。

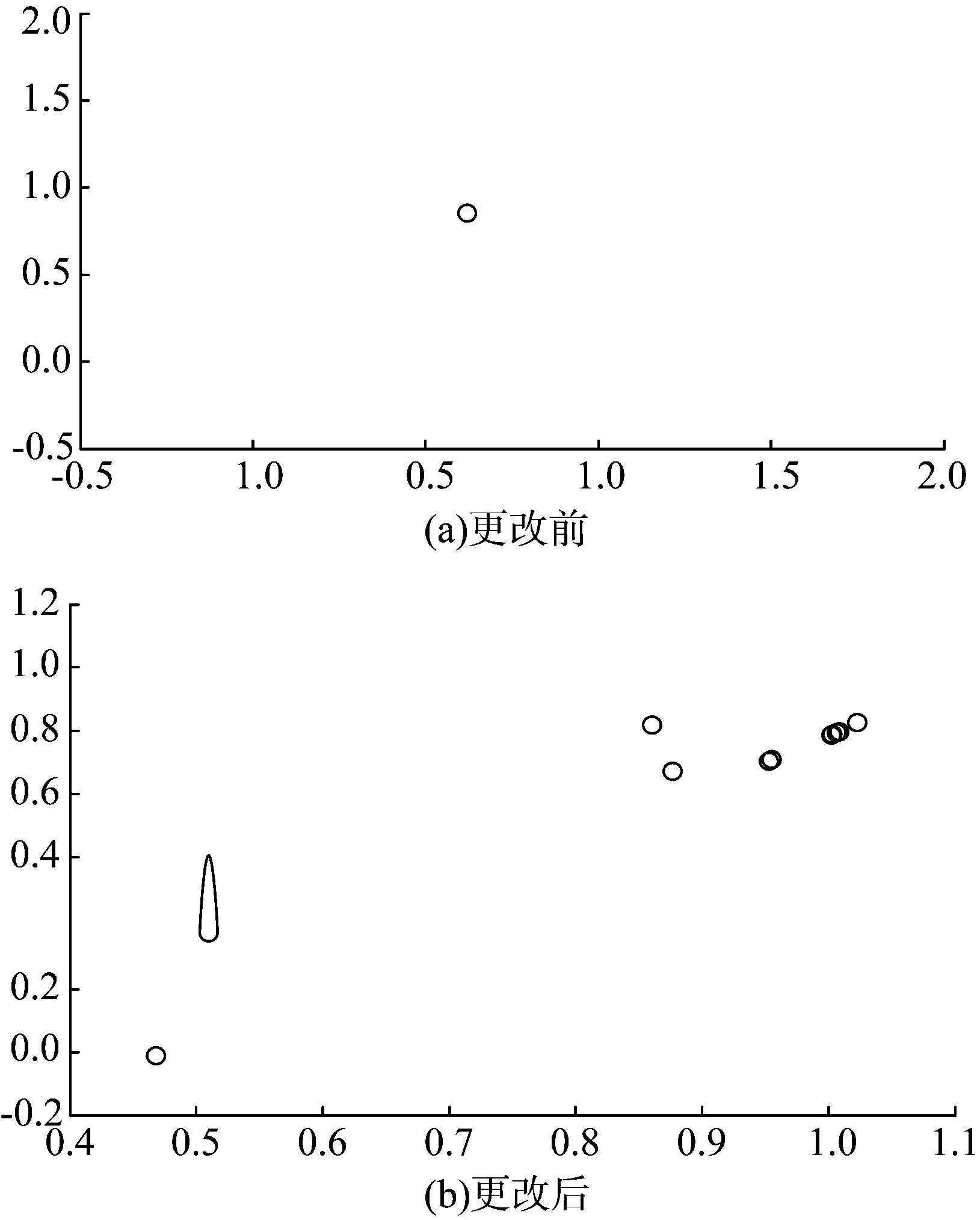
图1 蝙蝠 i的移动情况Fig.1 Movement of bat i

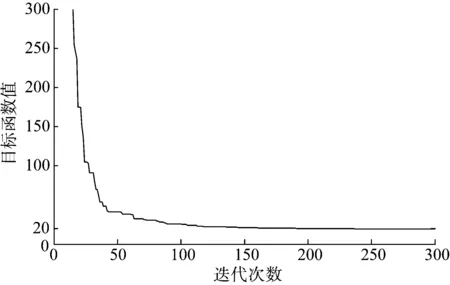
图2 采用IBA算法的测试函数寻优曲线(D=20，n=80)Fig.2 Test function optimization curve in IBA algorithm(D=20, n=80)表1 Rosenbrock测试函数仿真测试结果Table 1 Simulation test results of Rosenbrock test function

基于IBA算法的分布式电源选址和定容的流程图如图3所示。

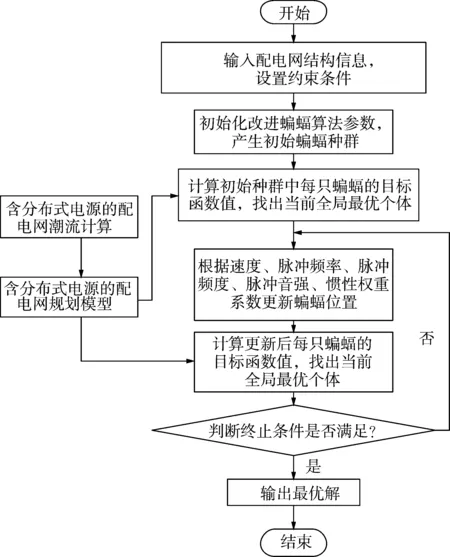
图3 基于改进蝙蝠算法的流程图Fig.3 Flow chart of modified bat algorithm

3 算例分析

3.1 算例

本文采用14节点配电网测试系统作为算例系统进行分布式电源的选址和定容分析。如图4所示，分布式电源待安装节点位置为3，4，10，14，该系统的电压等级为23 kV，Ptotal=28.7 MW，Qtotal=7.75Mvar。按照PDG≤0.25Ptotal，取PDG=3 MW，cosφ=0.9，每台分布式电源的额定功率为200 kW，电压偏差规定在±5%以内。

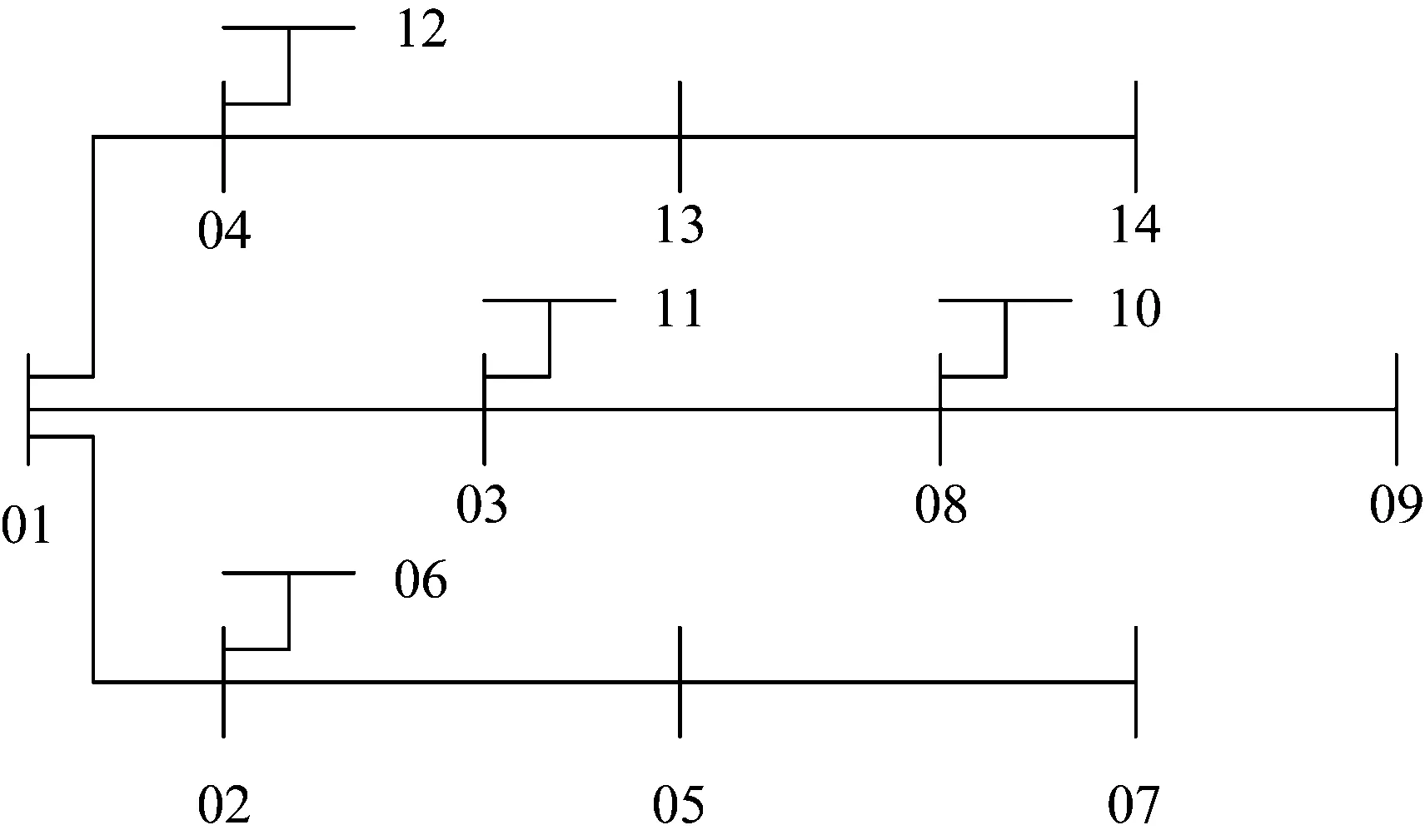
图4 14节点辐射型配电系统Fig.4 14-node radial distribution system

改进蝙蝠算法中参数选取如下：种群大小n=50，搜索脉冲频率最大值fmax=1、最小值fmin=-1，最大脉冲频度r0=0.5，最大迭代次数Tmax=1 000，脉冲频度增加系数γ=0.05，脉冲音强衰减系数α=0.95，最大脉冲音强Amax=0.25，惯性权重起始值ωstart=0.9，惯性权重终止ωend=0.4，惯性权重相关系数c=0.8。

第i个DG的安装成本CDG1i=1 344 元/kW；第i个DG的运行维护费用成本CDG2i=0.052 元/kW；第i个DG的发电燃料费用成本CDG3i=0.3 元/kW。模糊权重系数分别为a=0.4、b=0.3、c=0.3。

3.2 测试和结果分析

图5为采用BA、PSO和IBA算法对含分布式电源的配电网规划进行优化时的收敛特性曲线。从图5可以看出，PSO算法在迭代次数达到200次左右就已经收敛，但收敛的结果远差于IBA算法；而BA算法在迭代次数达到800次左右才得到最优解，且最优解的结果同样不如IBA算法。因此IBA算法在收敛速度和精度方面较前2种算法都有一定的优势。通过引入惯性权重系数和对判定条件的改进，有效地解决了BA算法易陷入局部最优，后期收敛速度较慢的问题。同时也说明了改进的蝙蝠算法应用于分布式电源的选址和定容是有效可行的。

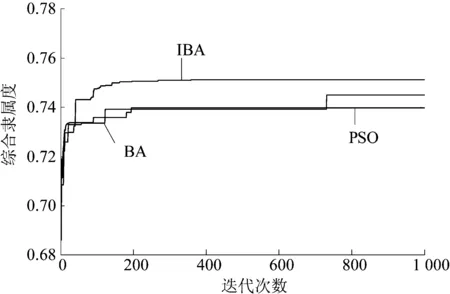
图5 采用BA、IBA和PSO后14节点配电网测试 系统的优化收敛曲线Fig.5 Optimization convergence curve of 14-node distribution network test system after using BA, IBA and PSO

表2为采用IBA算法进行分布式电源选址和定容得到的最优方案。从表2可看出：3，4，10，14节点最优输出功率分别为799.3，167.1，400，194.9 kW。根据实际设备制造情况，3，4，10，14节点应该分别安装4，1，2，1台分布式电源。每台分布式电源的额定功率为200 kW。通过采用最优规划方案，不但能够有效地降低网络的有功网损，减少分布式电源的建设和运行费用，而且还可以提高系统的电压水平。在无分布式电源时网络的有功网损为0.517 2 MW，网络的最低电压为0.971 3 pu，平均电压为0.984 2 pu；优化后的有功网损为0.413 1 MW，网络的最低电压为0.974 0 pu，平均电压为0.985 4 pu。对比无分布式电源时，网络的有功网损降低了20.1%，有效节省了电网的运行费用，这对实现配电网的经济稳定运行有着重要的影响。图6为14节点配电网系统优化前后各节点的电压水平分布。从图6可看出，优化后系统的电压质量有了明显的提高，这样有助于保证电网的可靠稳定运行。

表2 采用IBA算法优化14节点系统DG安装位置和容量

Table 2 Installation location and capacity of DG in 14-node system with using IBA algorithm

按照上文所建的多目标模糊规划模型，表3中分别取了4种方案进行比较，方案1是以分布式电源建设和运行总费用为目标函数的规划结果；方案2是以系统有功网损为目标函数的规划结果；方案3是以静态电压稳定指标为目标函数的规划结果；方案4为多目标模糊规划结果。从表3可看出：方案1在降低有功网损和改善电压质量上的帮助微乎其微，不利于电网的经济、稳定运行；方案2是以有功网损为目标函数进行优化，但是相应的分布式电源建设和运行总费用太高，不符合电网经济运行的要求；方案3强调改善静态电压稳定性，但是对分布式电源建设和运行总费用要求比方案2更高；方案4虽然对应的3个优化子目标都不是最好的，但是其综合隶属度要比方案1，2，3高很多，并且使3个子目标都得到了不同程度的改善，很好地协调了各优化目标之间的关系，从而为表达决策者意愿提供方便。

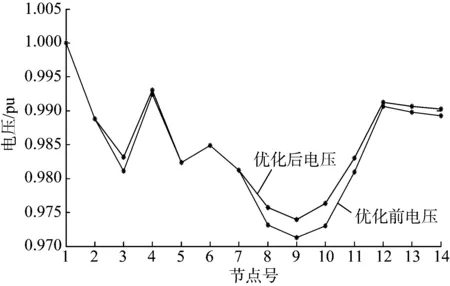
图6 14节点配电系统优化前后各节点电压水平分布Fig.6 Distribution of node voltage before and after 14-node distribution system optimization

表3 方案比较

Table 3 Scheme comparison

4 结 论

(1)本文综合考虑分布式电源建设和运行总费用、系统有功网损和静态电压稳定指标这3个方面，利用权重系数法建立了配电网分布式电源选址和定容规划模型。

(2)通过向基本蝙蝠算法中引入惯性权重系数和对判定条件的改进，有效解决了基本蝙蝠算法容易陷入局部最优、发生过早收敛、后期收敛速度慢的问题。

(3)本文将改进的蝙蝠算法应用于配电网的分布式电源规划，表明了改进的蝙蝠算法用于配电网分布式电源的选址和定容是有效可行的。

[1]庄园,王磊.分布式电源在配电网络中优化选址与定容的研究[J].电力系统保护与控制,2012,40(20):73-78.Zhuang Yuan，Wang Lei.Research of distributed generation optimal layout and capacity confirmation in distribution network[J].Power System Protection and Control, 2012,40(20):73-78.

[2]Mendez Q V H，Rivier A J，Gomez S R T.Assessment of energy distribution losses for increasing penetration of distributed generation[J].IEEE Transactions on Power Systems，2006，21(2)：533-540.余娟，孙鸣，邓博.DG的孤岛运行方式及其对保护与控制的影响[J].电力建设，2009,30(6)：21-24.

[3]Yu Juan, Sun Ming, Deng Bo.DG islet operation mode and its impact on protection and control[J].Electric Power Construction,2009,30(6):21-24.

[4]汪宁渤，马彦宏，王建东.大规模风电集中并网对电力系统安全稳定的影响[J].电力建设，2011，32(11)：77-80.Wang Ningbo, Ma Yanhong, Wang Jiandong.Analysis of power system security and stability caused by large-scale wind power grid integration[J].Electric Power Construction,2011,32(11):77-80.

[5]邱晓燕，夏莉丽，李兴源.智能电网建设中分布式电源的规划[J].电网技术，2010，34(4)：7-10.Qiu Xiaoyan, Xia Lili, Li Xingyuan.Planning of distributed generation in construction of smart grid[J].Power System Technology, 2010，34(4)：7-10.

[6]张节潭，程浩忠，姚良忠，等.分布式风电源选址定容规划研究[J].中国电机工程学报, 2009, 29(16): 1-7.Zhang Jietan, Cheng Haozhong, Yao Liangzhong, et al.Study on siting and sizing of distributed wind generation[J].Proceedings of the CSEE, 2009，29(16)：1-7.

[7]叶德意,何正友, 臧天磊.基于自适应变异粒子群算法的分布式电源选址与容量确定[J].电网技术, 2011, 35(6): 154-159.Ye Deyi，He Zhengyou，Zang Tianlei.Siting and sizing of distributed generation planning based on adaptive mutation particle swarm optimization algorithm[J].Power System Technology, 2011, 35(6): 154-159.

[8]丁明,石雪梅.基于遗传算法的电力市场环境下电源规划的研究[J].中国电机工程学报, 2006, 26(21): 43-49.Ding Ming，Shi Xuemei.Study of Generation expansion planning based on genetic algorithms in the environment of electricity market[J].Proceeding of the CSEE, 2006, 26(21): 43-49.

[9]Yang X S .A new metaheuristic bat-inspired algorithm [M]// Nature Inspired Cooperative Strategies for Optimization.Berlin: Springer-Verlag，2010：65-74.

[10]Bora T C，Coelho L D S，Lebensztajn L.Bat-inspired optimization approach for the brushless DC wheel motor problem[J].IEEE Transactions on Magnetics，2012， 48(2)：947-950.

[11]黄光球，赵魏娟，陆秋琴.求解大规模优化问题的可全局收敛蝙蝠算法[J].计算机应用研究，2013，30(5)：1323-1328.Huang Guangqiu，Zhao Weijuan，Lu Qiuqin.Bat algorithm with global convergence for solving large-scale optimization problem[J].Application Research of Computers, 2013，30(5)：1323-1328.

[12]Hamid F，Mahmood-Reza H.ACO based algorithm for distributed generation sources allocation and sizing in distribution systems[C]//2007 IEEE Power Tech.Lausanne：2007：555-560.

[13]盛晓华，叶春明.蝙蝠算法在PFSP调度问题中的应用研究[J].工业工程，2013，16(1)：119-124.Sheng Xiaohua，Ye Chunming .Application of bat algorithm to permutation flow-shop scheduling problem[J].Industrial Engineering Journal, 2013，16(1)：119-124.

[14]李枝勇，马良，张惠珍.0-1规划问题的元胞蝙蝠算法[J].计算机应用研究，2013，30(10)：2093-2906.Li Zhiyong，Ma Liang，Zhang Huizhen.Cellular bat algorithm for 0-1 programming problem[J].Application Research of Computers, 2013，30(10)：2093-2906.

[15]刘长平，叶春明.具有混沌搜索策略的蝙蝠优化算法及性能仿真[J].系统仿真学报，2013，25(6)：1183-1188.Liu Changping, Ye Chunming.Bat algorithm with chaotic search strategy and analysis of its property[J].Journal of System Simulation, 2013，25(6)：1183-1188.

[16]刘长平，叶春明，刘满城.来自大自然的寻优策略：像蝙蝠一样感知[J].计算机应用研究，2013，30(5)：1320-1322.Liu Changping，Ye Chunming，Liu Mancheng.Optimization strategy from nature: Perceive as bat[J].Application Research of Computers, 2013，30(5)：1320-1322.

(编辑：蒋毅恒)

Distributed Generation Planning for Distribution Network Based on Modified Bat Algorithm

FAN Bin, ZHOU Lixing, HUANG Di, LIU Jiajun, LIU Bowei, ZHU Lingfeng

(College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114, China)

Rational planning of distributed generation in power grid can improve the energy efficiency and the economy, reliability and flexibility operation of power system.This paper constructed the multi-objective planning model with minimizing total investment cost in the construction and operation of the distributed power system and the power loss of system, as well as maximizing the investment the static voltage stability index as optimization subgoals.This paper used and improved a new bionic algorithm-bat algorithm, which could effectively solve the problems of easily trapping into local optimal solution and slow convergence speed in the later stage.Then, 14-node distribution network test systems were used to simulate and analyze the location and capacity of distributed generation.The simulation results show that, compared with the traditional bat algorithm and particle swarm optimization, the improved bat algorithm can better and faster get the optimal planning scheme of distributed generation connected to distribution network, which can validate the correctness and feasibility of the algorithm.

distributed generation; bat algorithm; multi-objective optimization; distribution network; optimal location

TM 715

A

1000-7229(2015)03-0123-06

10.3969/j.issn.1000-7229.2015.03.022

2014-09-22

2014-11-14

范彬(1990)，男，硕士研究生，研究方向为电气设备在线监测；

周力行(1964)，男，教授，主要从事高压设备绝缘在线监测研究工作；

黄頔(1990)，女，硕士研究生，研究方向为电气设备在线监测；

刘家郡(1990)，男，硕士研究生，研究方向为电气设备在线监测；

刘博伟(1990)，男，硕士研究生，研究方向为电气设备故障诊断与定位；

朱凌峰(1989)，男，硕士研究生，研究方向为电气设备在线监测。