双馈风电场穿透率及接入形式对系统稳定性的影响分析

朱洁，周海强

(河海大学能源与电气学院，南京市 211100)



双馈风电场穿透率及接入形式对系统稳定性的影响分析

朱洁，周海强

(河海大学能源与电气学院，南京市 211100)

为了研究双馈风电场穿透率及接入形式对系统稳定性的影响，首先给出了以微分代数方程描述的双馈风力发电机动力学模型，推导了全系统系数矩阵。然后，根据小干扰分析理论，计算了含风电场系统的特征值及参与因子，并确定系统的主导振荡模式。最后，以扩展的IEEE 3机9节点系统为例，对不同穿透率水平及不同接入形式下各振荡模式的阻尼变化进行了分析比较。研究表明，随着穿透率的增加，在原有同步机容量相应减小且系统未作补偿的情况下，与风电场电气距离较近的同步发电机功角稳定性有明显下降。在相同穿透率下，静止无功补偿器(static var compensator, SVC)补偿容量的增加对系统电压及功角稳定性均有明显改善作用，穿透率水平越高，SVC无功补偿对稳定性的改善作用越弱。由此可知，双馈风电场穿透率及接入形式对系统稳定性有较大影响。

双馈风电场；穿透率 ；接入形式；小干扰稳定性

0 引 言

近年来，随着环境与资源压力的加大，风电作为一种可再生能源，得到了大力发展。双馈感应风力发电机(doubly fed induction generator, DFIG)应用矢量控制技术，可实现输出有功、无功功率的解耦控制，变流器容量仅为额定容量的25%左右，具有风能利用效率高、经济性好等优点，目前已成为风电场主流机型。大规模风电并网对系统的运行与稳定产生了多种影响：(1)风电具有随机性，风电场输出功率大幅波动，对系统备用功率及其响应速度提出了很高的要求；(2)风速的变化将导致系统稳态平衡点不断迁移，在特定平衡点附近作出的小干扰分析结果也随之发生改变；(3)风电接入后，与原有同步发电机相互作用，将导致原有运动模式的变化，并引入新的运动模式，这就使得系统的稳定性问题变得更为复杂；(4)故障后风电场需要从系统吸纳大量无功，这对系统的电压稳定性的影响不利。

风电并网可以有多种接入形式，输电方式主要有高压直流并网(单极型和双极型)、高压交流并网等，不同电网会根据实际情况决定是否进行静止无功补偿器(static var compensator, SVC)补偿以及风电接入后原有同步发电机容量及惯性时间常数是否作相应减小等。不同输电方式、补偿方式及同步机运行方式可以组合成各种不同的接入形式。在不同的穿透率水平和接入形式下，风电场对系统稳定性的影响各不相同。因此，详细分析风电接入后对系统稳定性的影响是风电发展亟需解决的问题。

国内外学者对此开展了大量研究，文献[1]提出了保证电网和风电场安全稳定运行的风电场安全容量的概念，并给出了计算方法，同时指出，加装SVC可以提高风电场的安全容量。文献[2]提出了DFIG 和同步发电机功角摇摆曲线的主动和被动交越点的概念，指出主动交越点可提高同步发电机的稳定性，而被动交越点则降低了同步发电机的稳定性。文献[3]研究了常见的3类风电机组接入后系统稳定性，认为与同步发电机组相比，3类风电机组的接入均能不同程度的提高系统机电振荡模式的阻尼比。文献[4]则认为风电接入增加了系统振荡阻尼且风电机没有产生新的振荡模式。文献[5]用时域仿真法研究了DFIG与同步发电机并列接入弱联接电网时对稳定性的影响，得出了DFIG接入没有降低电网稳定性的结论。文献[6]应用系统特征值对惯性时间常数的灵敏度分析了风电穿透率增加对系统稳定性的影响。总的说来，目前的研究主要集中于不同穿透率时风电接入后系统振荡模式的变化，对不同接入形式对多机系统稳定性的影响考虑较少。由于各项研究的假设条件不同，所得结论差异很大，还有待进一步验证。

本文重点分析2种不同接入形式下风电系统的稳定性。在DFIG数学模型的基础上，根据不同物理过程的时间尺度对其进行适当化简，并结合同步发电机数学模型，推导以微分代数方程组描述的全系统动力学模型。以IEEE 3机9节点系统为例，计算风电接入后的特征根及参与因子，对不同穿透率水平下的系统各振荡模式的频率、阻尼进行分析，对SVC补偿、同步机容量是否调整等不同接入形式下的稳定性进行比较。

1 DFIG运行原理及动力学模型

DFIG包括风力机、感应发电机及变流器三大部分。感应发电机转子绕组通过2个背靠背连接的双脉宽调制流器与电网连接，利用矢量控制技术，可分别调节转子电流的d、q分量以控制DFIG输出有功及无功功率的大小，实现PQ解耦控制。通过对电网侧变流器的控制，可以保持直流电容的电压恒定，并使DFIG运行在单位功率因数。文献[7-9]详细描述了DFIG运行机理，本节将作简要说明，给出各环节的数学模型。

文中采用电动机惯例，以电流流入节点为正。DFIG中直流电容、电容电压取有名值，其他各变量、参数均为基于DFIG额定容量Swt及额定电压的标幺值。下文以下标s、r表示定子及转子变量，以下标x、y表示变量的公共坐标系分量，以d、q表示直轴与交轴分量。例如，ird即为转子电流的直轴分量。

为简化分析，不考虑桨距角控制环节，并忽略风力机转轴与感应发电机转轴之间的扭转作用，将风电机组转子视为单刚体。这样，DFIG的机械运动可表示为

(1)

式中：Hg、Ht分别为感应发电机、风力机惯性时间常数；ωr为转子转速；ρ、A及υ分别为空气密度、叶片面积及风速；风能利用系数Cp为叶尖速比λ及桨距角β的非线性函数；Lm、Ls分别为定转子互感及定子自感；ψs为定子磁链；D为阻尼。

DFIG转子电流一般采用定子磁链定向控制策略[8]，在定子磁链定向坐标下，ψsd=ψs、ψsq=0，据此可得

(2)

式中：Te为电磁转矩；Qs为定子无功功率。

对于感应发电机，若忽略定子电磁暂态(即假设dψs/dt=0)，并认为定子电阻近似为0，则Us=jωsψs，ωs为同步转速。在标幺制下，ωs=1，故Us、ψs幅值近似相等，相位相差90°。转子电流的变化规律为：

(3)

式中：ωslip=ωsωr为转差率；σ=1-Lm2/(LrLs)为漏磁系数；Rr为转子电阻；Lr为转子自感。urd、urq为转子侧变流器的输出电压。

转子侧变流器控制器包括功率外环、电流内环2个串联的PI控制环节。式(4)描述了根据转子转速ωr与ωr,ref的差值调节urq及irq的原理

(4)

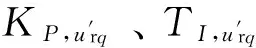
(5)

网侧变流器的控制目标是保持直流电容电压恒定，且控制输入功率因数，一般采用电网电压定向(stator voltage orientation,SVO)矢量控制，d轴定向于电网电压，即：usd=Us,usq=0。网侧变流器采用电压外环和电流内环的控制方案。由于电流内环的响应较外环要快很多，在小扰动分析中常忽略其动态过程。一般设ilq,ref为0，即进线功率因数为1，DFIG仅通过定子与电网交换无功功率。电网侧变流器控制环节的数学模型为

(6)

式中：Cdc为直流电容；Udc为直流电压；Rl、Xl为进线电抗器的电阻及感抗；ild,ilq为进线电流的d,q分量；KP,Udc、TI,Udc为电容电压控制环节的增益与时间常数；xUdc为中间变量；Swt为双馈风力发电机额定容量，该环节输出为ild,ref。式(6)第2行等号右边第1项为输入功率，第2项为输出到转子的负荷功率。

式(1)～(6)构成了9阶的DFIG动力学模型。大型风电场的分析常需要先进行等值，研究表明，一般用3台等值风电机来描述风电场可得到较满意的精度[10]，将等值风电机依据上述方法分别建模即可得出风电场的数学模型。

2 双馈风电系统小干扰分析

小干扰分析时，一般将电力系统在其稳态运行点附近线性化，计算系统状态矩阵，根据其特征值、特征向量及参与因子等来分析系统各振荡模式的性质及小干扰稳定性。本文中同步发电机采用3阶模型，励磁系统为3阶模型。文献[11-14]详细介绍了同步发电机、调速器及励磁系统的工作原理及建模方法，限于篇幅，此处不再赘述。

由于DFIG转子侧、网侧变流器分别采用SFO、SVO矢量控制策略，在进行全系统分析时将统一变换到xy公共坐标系。DFIG中不同坐标系角度关系如图1所示，设d轴超前x轴δ角，则对于任意变量ξ，其dq轴分量与xy坐标系分量的变换公式为

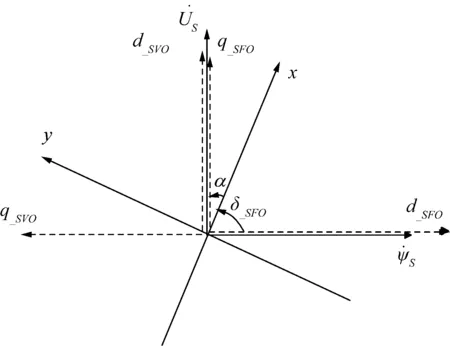
图1 不同坐标系的转换关系Fig.1 Transformation of different reference frames

显然，若DFIG机端电压为Usα，则在SVO坐标系中，δ=α；在SFO坐标系中，δ=α-π/2。

分别定义与DFIG相关的状态变量、代数变量及机端电压

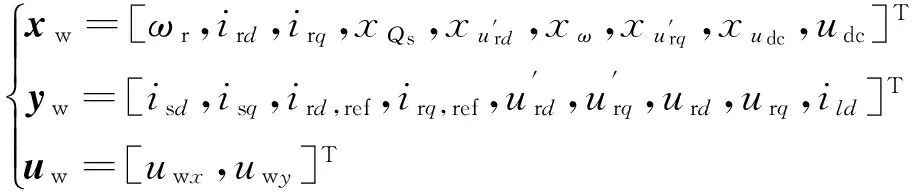
则式(1)～(6)可简写为

(7)

将其在稳态值附近线性化，可得

(8)

式中：J11、J12、J13与J21、J22、J23分别为fw与gw对xw、yw、uw的偏导数。由式(8)可导出

(9)

式中：AW=J11-J12J22-1J21，FW=J13-J12J22-1J23。

将所得风电场线性化模型与同步发电机线性化模型联列，可推导出系统的全状态矩阵A，进一步计算出其特征值λ、左特征向量νT和右特征向量u，求出参与因子矩阵P=(pk,i)n×n，其中

pk,i=vkiuki

(10)

在此基础上可分析风电系统的小干扰稳定性。

3 算例分析

本节结合具体算例，分析了不同穿透率及接入形式对系统稳定性的影响。算例系统如图2所示，双馈风电场由n台DFIG组成，单台DFIG额定容量为1.5 MVA，经2级升压后风电在节点9接入IEEE 3机9节点系统，DFIG及双馈风电场参数分别如附录A1、A2所示。

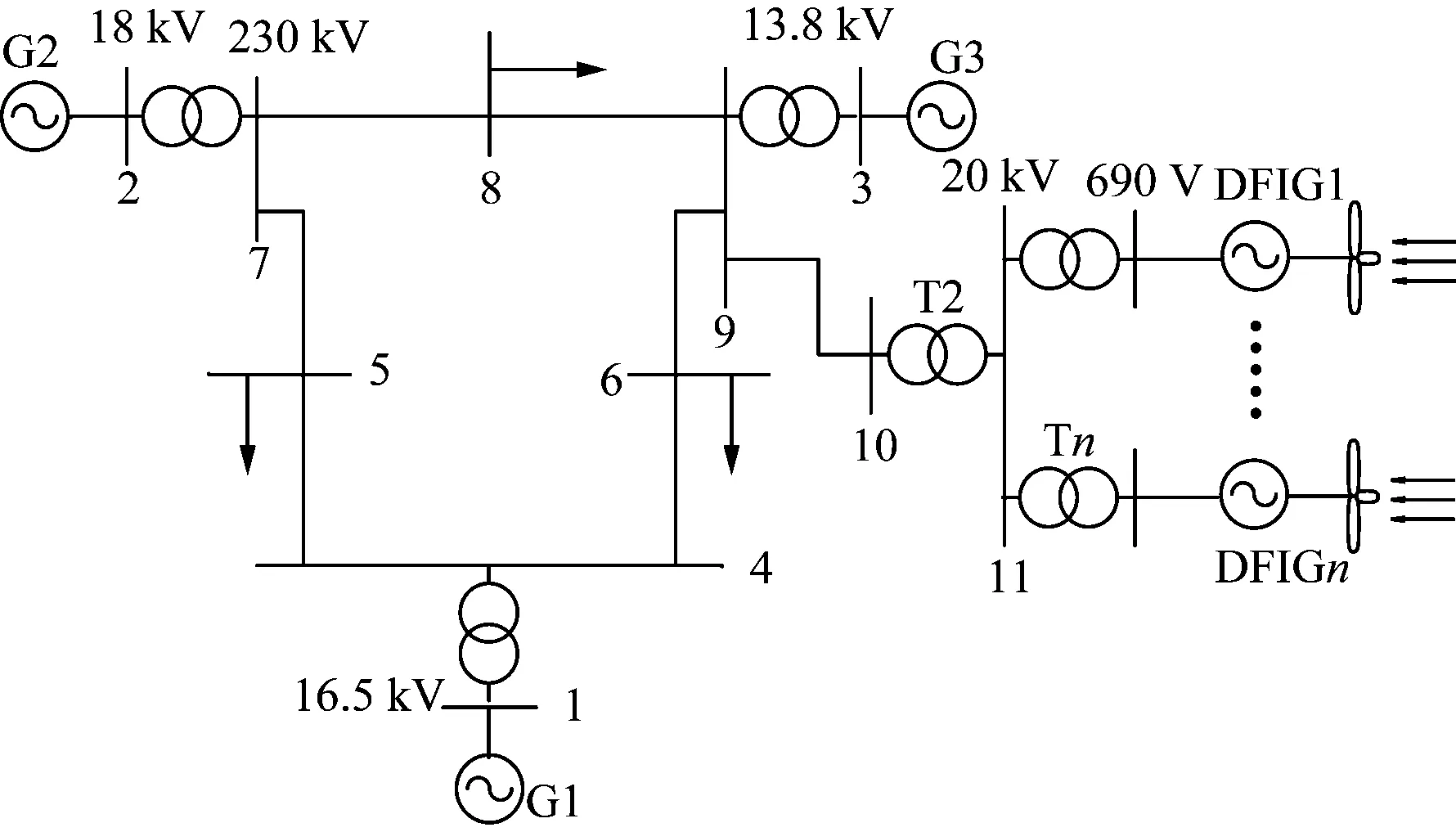
图2 基于IEEE 3机9节点系统的双馈风电场Fig.2 DFIG-based wind farm based on IEEE 3-generator and 9-bus system

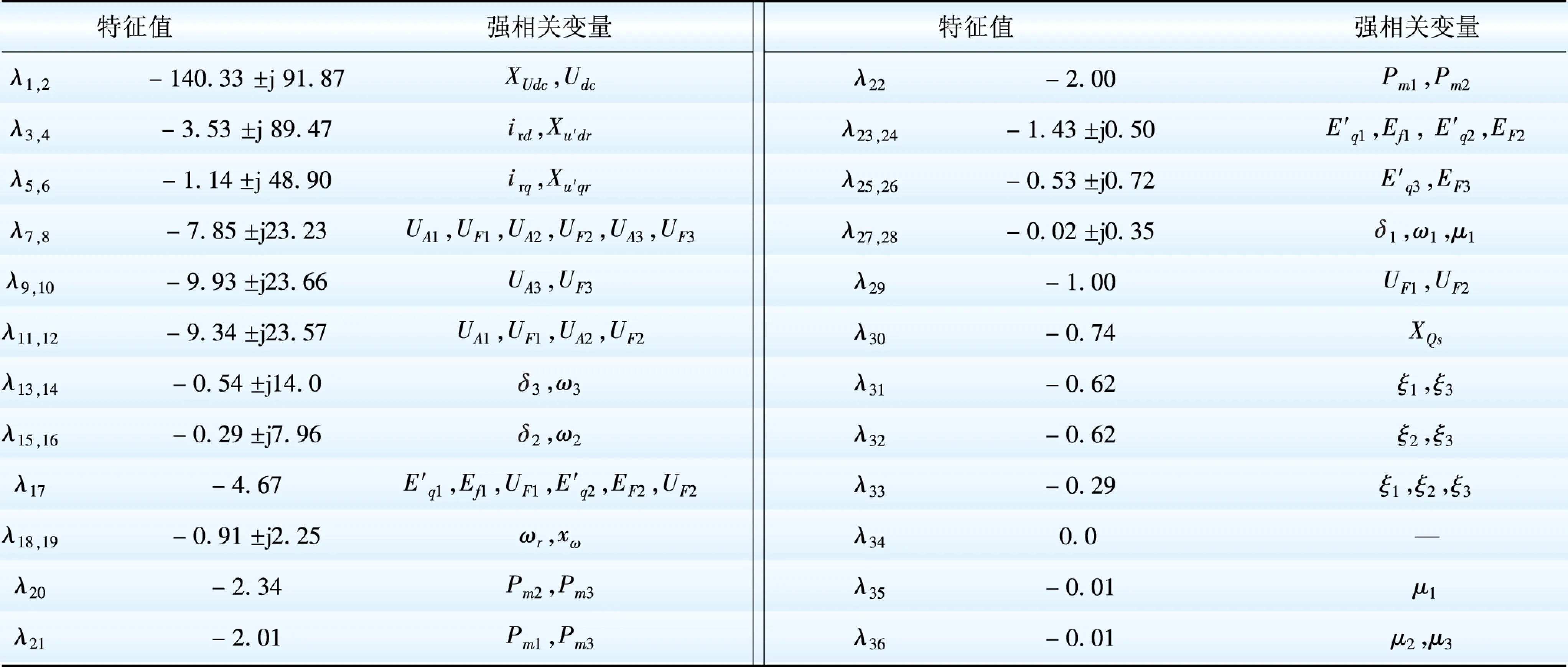
首先计算系统稳态运行点，根据注入风速及转速-功率曲线确定DFIG输出功率，对系统进行初始化[10]，然后对系统进行小扰动分析。附表B1中列出了装机总数为20台(风电场总容量为30 MVA)，风速υ=8 m/s时系统的全部特征值及相关变量。由于文中采用了绝对功角，故存在1个零特征值(λ34)，如使用相对功角则可将其消去。由附表B1可知，所有特征值均具有负实部，系统稳定。下面对2种接入形式下系统的稳定性进行分析：接入形式I加大风电穿透率的同时，相应减小相邻同发电机G3的容量及惯性时间常数；接入形式II在PCC点进行不同程度的SVC补偿。

3.1 接入形式I

在接入形式Ⅰ下，风电场穿透率增加的同时，相应减小同步发电机的容量及惯性时间常数，从而达到新的功率平衡点。图3(a)、(b)分别给出了风电场装机总数n由1逐步增加到50时，系统中与功角振荡、电压振荡强相关的特征值根轨迹图。

由图3(a)可知，随着n的增加，由于发电机G3的容量减小，转子惯性时间常数减小，δ3对应振荡模式λ13,14频率增加，阻尼减小。δ2对应振荡模式λ15,16以及G1与G2之间的区域振荡对应模式λ27,28变化相对较小，随着风电比例的提高，其阻尼比略有减小。

由图3(b)可见，系统包含的3个与电压相关的振荡模式衰减均较快。随着n增长，与母线2电压强相关的实根λ17向虚轴移动，λ23,24经历了阻尼比由减小到增大的过程，与母线3电压相关的λ25,26阻尼比则持续增大。

由上述分析可知，风电穿透率增加对各种运动模式的影响不一，就本文算例而言，穿透率对功角稳定性的影响较其对电压稳定性的影响更为显著。在接入形式Ⅰ下，与风电场相邻的同步发电机功角振荡模式阻尼比显著减小，频率增加，不利于系统功角稳定。

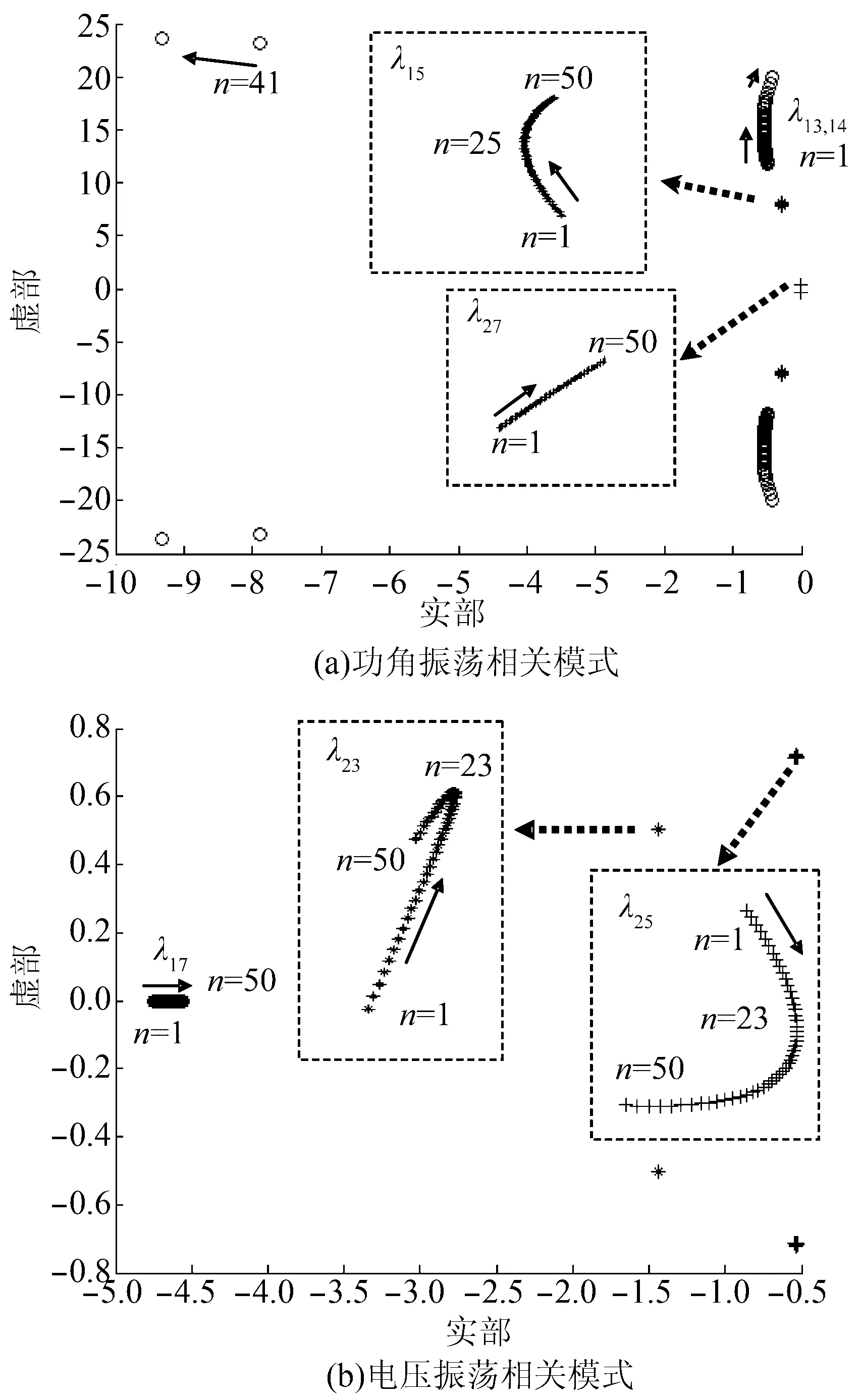
图3 n变化时系统的部分特征值根轨迹图Fig.3 Root locus diagram of parts of system’s eigenvalues during n changing

3.2 接入形式Ⅱ

在该接入形式下，在PCC点对系统进行SVC无功补偿。改变风电场穿透率及SVC补偿容量，观察与δ2、δ3及U2、U3相关的运动模式的变化情况。表1给出了风电场穿透率为4.76%、14.29%和23.8%时，不同补偿程度时系统特征值的变化情况。

由表1可知，在风电穿透率γ为4.76%、14.29%及23.8%时，随着SVC补偿容量的增加，与δ2、δ3及U2、U3强相关的特征值负实部的绝对值均有不同程度的增长，而虚部则变化不大。因此，进行SVC补偿可以同时提高同步发电机的功角和电压稳定性，且从阻尼比来看，SVC无功补偿提高电压稳定性的作用更为显著。同时，由表1还可以看到，风电穿透率为23.8%时，SVC补偿所引起的阻尼增加比穿透率为4.76%、14.29%时要小得多。在不同穿透率水平下，相同的SVC无功补偿对系统稳定性的改善效果相差很大。随着风电穿透率水平的提高，SVC补偿提高系统稳定性的效果减弱。

表1 不同穿透率及补偿容量时系统特征值

Table 1 Eigenvalues with different penetration rates and compensations

4 结 论

(1)在同步机容量及惯性时间常数随着双馈风电场穿透率的增加作相应减小时，风电接入对相邻同步发电机的功角稳定性较为不利。

(2)在PCC点加装SVC无功补偿装置，可有效改善系统的功角及电压稳定性；风电穿透率越大，相同SVC补偿对系统稳定性的改善效果越弱。风电场对系统稳定性的影响非常复杂，不仅与风电穿透率水平和网络拓扑结构有关，还受到传输方式、补偿容量及同步机运行方式等多种因素的影响。

[1]张红光，张粒子，陈树勇，等.大容量风电场接入电网的暂态稳定特性和调度对策研究[J].中国电机工程学报，2007，31(13):75-80.Zhang Hongguang，Zhang Lizi，Chen Shuyong，et al.Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms[J].Proceedings of the CSEE，2007，27(31):45-51.

[2]郝正航，余贻鑫.双馈风力发电机组对电力系统稳定性影响[J].电力系统保护与控制，2011，39(3):7-11.Hao Zhenghang，Yu Yixin.The influence of doubly-fed induction generator on stability of power system[J].Power System Protection and Control，2011，39(3):7-11.

[3]和萍，文福拴，薛禹胜，等.不同类型风电机组对小干扰和暂态稳定性的影响[J].电力系统自动化，2013，37(17):23-29.He Ping，Wen Fushuan，Xue Yusheng，et al.Impacts of different wind power generators on power system small signal and transient stability[J].Automation of Electric Power Systems，2013，37(17):23-29.

[4]Slootweg J G，Kling W L.The impact of large scale wind power generation on power system oscillations[J].Electric Power Systems Research，2003(67):9-20.

[5]Muljadi E，Butterfield C P，Parsons B，et al.Effect of variable speed wind turbine generator on stability of a weak grid[J].IEEE Transactions on Energy Conversion，2008，22(1):29-35.

[6]Gautam D，Vittal V，Harbour T.Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J].IEEE Transactions on Power Systems，2009，24(3):1426-1434.

[7]Pena R，Clare J C，Asher G M.Doubly fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation[J].IEEE Proceedings:Electric Power Applications, 1996，143(5):380-387.

[8]贺益康，胡家兵，徐烈.并网双馈异步风力发电机运行控制[M].北京：中国电力出版社，2012:39-92.

[9]姚兴佳，宋俊，邢作霞.风力发电机组原理与应用[M].北京：机械工业出版社，2009:191-260.

[10]周海强，张明山，薛禹胜，等.基于戴维南电路的双馈风电场动态等值方法[J].电力系统自动化，2012，36(23):42-47.Zhou Haiqiang，Zhang Mingshan，Xueyusheng，et al.A dynamic equivalent method for Doubly-fed Induction Generator windfarm based on the Thevenin equivalent circuit[J].Automation of Electric Power Systems，2012，36(23):42-47.

[11]倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析[M].北京：清华大学出版社，2002:1-80.

[12]王锡凡，方万良，杜正春.现代电力系统分析[M].北京：科学出版社，2003:240-283.

[13]汪宁渤，马彦宏，王建东.大规模风电集中并网对电力系统安全稳定的影响[J]，电力建设，2011，32(11):77-80.Wang Ningbo，Ma Yanhong，Wang Jiandong.Analysis of power system security and stability caused by large-scale wind power grid integration[J].Electric Power Construction，2011，32(11):77-80.

[14]李军军，吴政球，谭琼，等.风力发电及其技术发展综述[J]，电力建设，2011，32(8):64-72.Li Junjun，Wu Zhengqiu，Tan Xunqiong，et al.Review of wind power generation and relative technology development[J].Electric Power Construction，2011，32(8):77-80.

朱 洁(1990)，女，硕士研究生，主要研究方向为风电场建模;

周海强(1971)，男，博士，副教授，主要研究方向为电力系统稳定与控制。

(编辑：蒋毅恒)

附录 A 双馈风电场及风电机参数

A1 双馈风电机参数

风力发电机额定功率Swt=1.5 MW，额定电压为690 V；DFIG参数 [Rs,Xls,Rr,Xlr,Xm] =[0.005 4, 0.1, 0.006 07, 0.11, 4.5]；2(Hg+Ht)=0.85 s；D=0.000 1。直流环节Cdc=7 800μF，Udc,ref=800 V，进线Rl=0，Ll=0.095 22。风机R=40 m,ρ=1.225,λ=10.9,Cp=0.28。

PWM变流器控制器参数：KP,ω=1，TI ,ω=0.2；KP,Qs=0.5，TI,Qs=0.2；KP,Udc=0.001，TI,Udc=0.01；KP,u’rd=0.5，TI,u’rd=0.001；KP,u’rq=0.5，TI,u’rq=0.001。网侧变流器调制比m=0.75。

A2 双馈风电场参数

变压器T1变比为0.69/20kV，容量为1.5MVA，XT1=0.06pu；T2变比为20/230kV，容量为1.5MVA，XT2=0.08pu。风电场PCC(母线10)至系统接入点(母线9)R9,10=0.033 7，X9,10=0.593 3，B9,10=0.193 3 pu。

附录 B 算例系统特征值及其相关变量

表B1n=20,υ=8m/s时系统的特征值及其强相关变量

Impacts of Penetration Rate and Integration Methods of DFIG-Based Wind Farm on System Stability

ZHU Jie，ZHOU Haiqiang

(College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China)

To study the impacts of penetration rate and integration methods of DFIG-based (doubly fed induction generator) wind farm on system stability, firstly, the dynamic model of doubly-fed induction generator was described by the differential algebraic equations, and the coefficient matrix of total system was derived.Then, the eigenvalue and participation factors of wind farm system were calculated according to the small signal analysis theory, and the dominant oscillation modes of system were determined.Finally, taking augmented IEEE 3-generator and 9-bus test system as example, the damping changes of electromechanical oscillation modes were analyzed under different penetration rates and various integration methods.The research results show that, the increasing of penetration rate of wind generation has a detrimental impact on the power angle stabilities of the adjacent synchronous machines when their capacities are reduced at the meantime and the system is without compensation.The stabilities of system’s voltage and power angle are improved greatly with the increasing of SVC (static var compensator) compensation capacity, under same penetration rate.The improving effect of the SVC compensation on the system stability will decrease with the increase of penetration rate.It follows that the penetration rate and integration methods of DFIG-based wind farm have great influences on the system stability.

DFIG-based wind farm; penetration rate; integration methods; small signal stability

国家重点基础研究发展计划项目(973项目)(2013CB228204)。

TM 712

A

1000-7229(2015)03-0015-06

10.3969/j.issn.1000-7229.2015.03.003

2014-11-26

2015-01-21

Project Supported by National Basic Research Program of China (973 Program)(2013CB228204).