双参数威布尔分布风况中基于k值分析的能量分布研究

姜广绪，潘晶雯，田景奎

(1.中国电力工程顾问集团华北电力设计院有限公司,北京市 100120；2.中国人民解放军装甲兵工程学院，北京市 100072)



双参数威布尔分布风况中基于k值分析的能量分布研究

姜广绪1，潘晶雯2，田景奎1

(1.中国电力工程顾问集团华北电力设计院有限公司,北京市 100120；2.中国人民解放军装甲兵工程学院，北京市 100072)

在风力发电场风能资源分析中，仅采用年平均风速和年平均风功率密度来判断风电场风能资源的好坏是不全面的，其无法体现风电场风能资源的能量输出能力。通过对单峰双参数威布尔分布风况中形状参数k值的研究，找出其与风速、风能频率分布及风中蕴含能量的关系，并进一步分析对于不同风力发电机组Cp值曲线，k值与总体有效风能利用率的关系，从而在风电场建设的咨询、决策、设计等阶段对风电场风能资源评估和风机预选型作出科学的指导。

威布尔分布；风力发电；能量分布；形状参数

0 引 言

风力发电场是将风能转化为机械能，再将机械能转化成电能的装置总成在一起的系统[1]。在风电场开发设计过程中，对场区内风能资源的评估研究是前期工作最重要的环节，这将从根本上决定风电场的优劣[2-3]。

实际工程中经常用年平均风速和年平均风功率密度来直观地评价某地的风能资源情况，这种直观的评价为风电场选址提供了重要依据[4-5]。但在实际工程中，仅利用年平均风速和年平均风功率密度评价风能资源有一定的偏差甚至评价结果与实际相反。例如，山西省北部和中部A、B这2个风场测风塔处80 m高年平均风速均为6.9 m/s，但A风场测风塔80 m高年平均风功率密度为393 W/m2，B风场的为278 W/m2。直观来看，显然是A风场较好，但对这2个测风塔处选用同种机型进行发电量计算发现，B的发电量要远高于A的发电量。

随着我国风电场的大规模建设，如何准确评估风能资源成为研究热点。文献[6]指出风功率密度等级的划分仅用风功率密度、年平均风速来要求存在一定的缺陷，并建议根据风场测风数据统计出的A、k值草拟《风功率密度等级和风能区等级划分标准》确定等级。 一些学者从风速频率分布的参数(如威布尔分布的k值)影响入手，研究了其对风速频率分布自身的影响[7]，这从理论上对风况自身的好坏评价可作出较好的分析。而实际上风力发电场毕竟是要通过能量转化装置即风力发电机组来将风能转化为电能，因此，上述研究很难结合风力发电机组的性能对风能资源的能量输出能力进行分析。文献[8]针对上述情况提出了相当风速和有功风功率密度这2个概念，结合风力发电机组的性能对风能资源情况进行评估。但上述研究仅限定在理论概念上，没有结合风速频率分布及分布参数的影响进行分析。

本文通过对双参数威布尔分布风况中形状参数k值的研究，找出其与风速频率分布、风能频率分布以及风电场能量输出能力之间的关系和相应规律，为风电场风能资源的评估提供科学依据。

1 理论基础

双参数威布尔分布被普遍认为是适用于描述风速分布统计的概率密度函数，其是一种单峰的、双参数分布函数簇[9]。风速概率密度函数可表达为

(1)

式中：k为形状参数，无量纲；c为尺度参数，m/s；v为风速，m/s。

风能公式为

(2)

式中ρ为空气密度，kg/m3。

由此可以推导平均风功率密度的数学期望E(w)[10-11]，假定空气密度一定,则

(3)

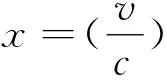
(4)

式中Г为伽马函数。

同理可以推导平均风速的数学期望：

(5)

即

(6)

将式(6)代入式(4)中可以得到：

(7)

(8)

2 k值与风中蕴含能量的关系

由公式(7)可知，某一符合双参数威布尔分布的风况中，其平均风功率密度与空气密度、平均风速和形状参数(即k值)有关。假定空气密度为定值不变，当平均风速一定时，平均风功率密度只与k值有关。

根据工程经验，中国的风电场k值一般为1.2～3[12]，本次选取1～5作为研究区段，以0.1作为步长对θ进行定量计算，结果如图1所示。

由图1可知，θ值随着k值的增大逐渐减小，当k趋近于∞时，θ值趋近于1，即对于服从双参数威布尔分布的风况，平均风速一定时，k值越小，风中蕴含的能量越多。

3 k值与风速、风能频率分布的关系

以平均风速7 m/s的风况为例，分别对k=1.5，2.0，2.5和3的风速频率分布情况进行分析，如图2所示。

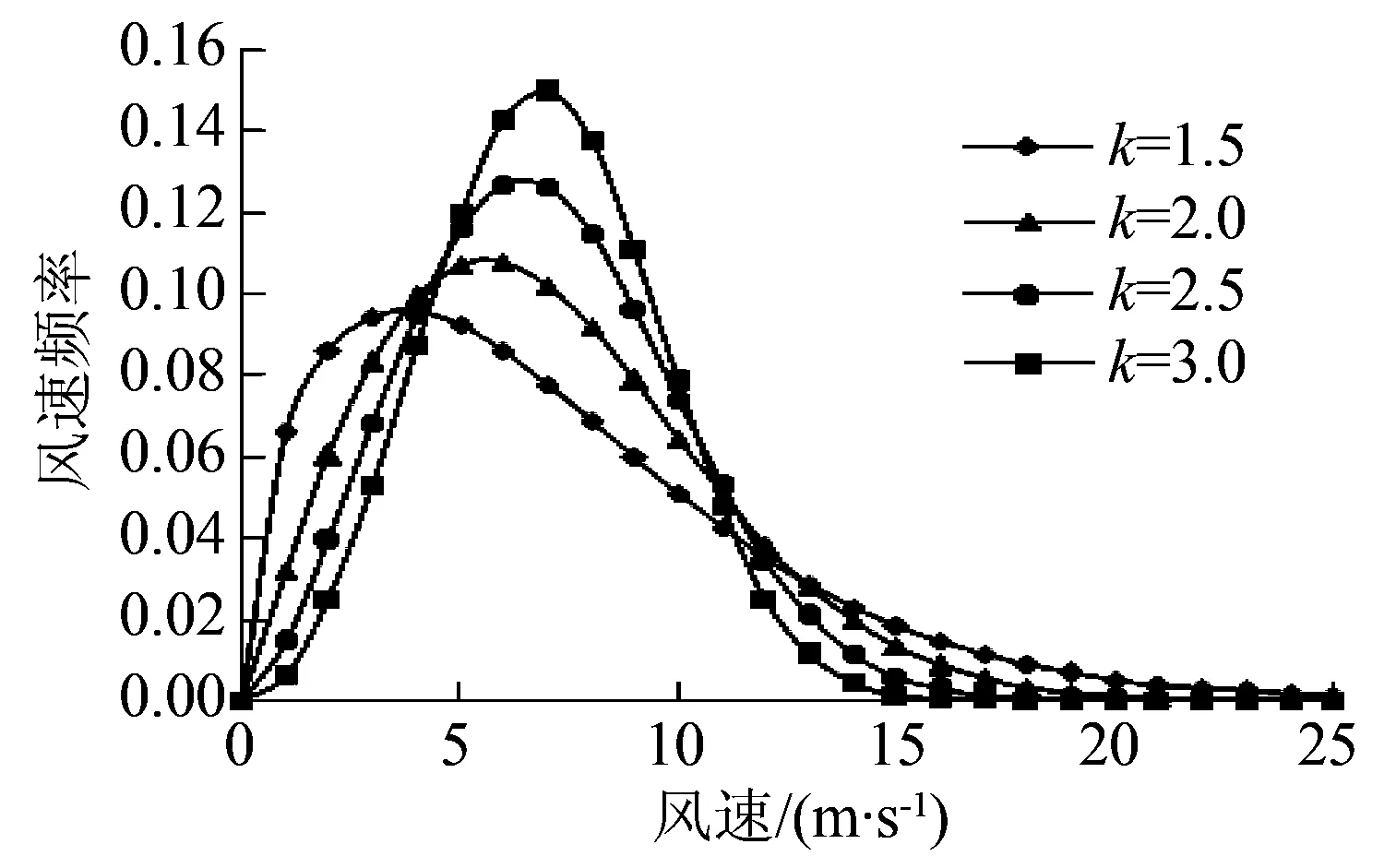
图2 风速频率分布随k值变化情况Fig.2 Wind speed frequency distribution with k value changes

由图2可知，在研究区域内，随着k值的增大，分布的峰值逐渐增大，且出现的风速区域越来越大并接近平均风速，同时小风速区域(0～5 m/s)频率逐渐减小，平均风速附近区域(5～11 m/s)频率逐渐增大，大风速区域(11 m/s以上)频率逐渐减小。也就是说k值越大，分布越集中，k值越小，分布越分散。这也可以从k值的估算公式上加以验证：

(9)

式中s为分布的标准差[13]。

可见k值越小，标准差s越大，说明数据分布越分散。

对上述风速频率分布分别作出相应的风能频率分布曲线，如图3所示。

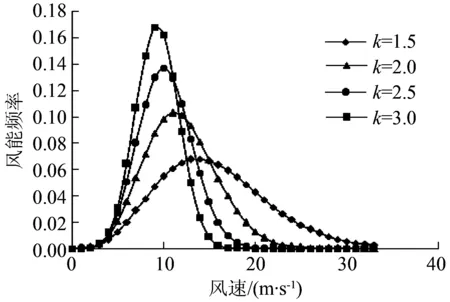
图3 风能频率分布随k值变化情况Fig.3 Wind energy frequency distribution with k value changes

从图3中可以看出，在研究区域内，随着k值的增大，分布的峰值逐渐增大且出现的风速区域越来越小并接近平均风速，同时小风速区域频率变化很小，平均风速附近区域频率逐渐增大，大风速区域频率逐渐减小。

由上述分析可知，在威布尔单峰双参数风况分布中，随着k值的减小，风中蕴含的能量逐渐增加，但同时能量的分布也越来越分散。

4 k值与总体有效风能利用率的关系

风力发电机组在变转速区(额定风速以下)需要通过变桨对转速进行相应控制，以达到较好的叶尖速比，从而提高相应的风能利用系数，即Cp值[14]。而在定转速区(额定风速以上)，为了稳定输出和安全性问题，又需要通过变桨使叶轮转速恒定，这就导致了叶尖速比随着来流风速的增加显著降低，导致了大风速区域风能利用系数较低[15]。图4给出了某风力发电机组的设计Cp曲线。

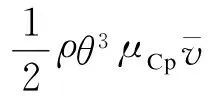
图4 某风力发电机组的Cp值曲线Fig.4 Cp curve of a kind of wind turbine

表1k值与总体有效风能利用率的对应表

Table 1 Correspondence table ofkand overall effective wind energy utilization

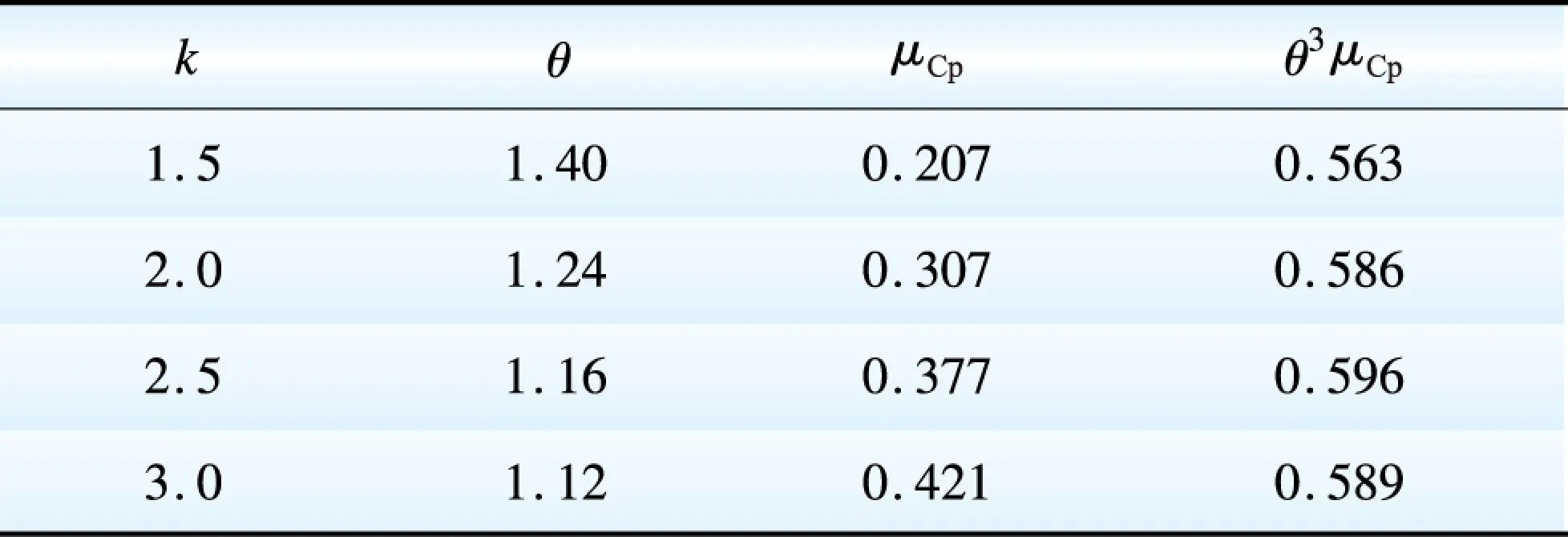
结合前述分析，当平均风速一定时，随着k值的减小，风力发电机组风能利用系数较大的小风速区域风能频率明显降低，而在风能频率显著增大的大风速区域，风能利用系数又很小，这就导致了表中μCp减小。因此随着k值的减小，虽然风中蕴含的风能逐渐增加(θ值变大)，但平均有效利用风功率密度却不是一直在增加，而是在达到某个最优值后逐渐减小。因此会出现相同的年平均风速，年平均风功率密度较高的风况下发电量反而较低的情况。

通过分析，发现针对特定的风力发电机组和平均风速，平均有效利用风功率密度存在一个最优值，相应也就存在一个最优k值。例如采用文中提到的机型，当平均风速为7 m/s时，对应的最优k值约为2.5；当平均风速为6.5 m/s时，对应的最优k值约为2.0；当平均风速为7.5 m/s时，对应的最优k值约为3.4。一般来说，平均风速越大，对应的最优k值也越大。在风力发电机组选型时，机组在实际平均风速下对应的最优k值越接近风场风况的实际k值，发电量也就越高。

进一步分析在低风速情况下，如平均风速为5.5 m/s时，其最优k值小于1.3，当k值为2.0时，其电量折合满发小时数约为2 202 h，如果有20%的发电量折减，则折合满发小时数仅为1 762 h；如平均风速为5 m/s时，其最优k值小于1.1，当k值为2.0时，其电量折合满发小时数约为1 765 h，如果有20%的发电量折减，则折合满发小时数仅为1 412 h。在服从双参数单峰威布尔分布风况下，平均风速小于5.5 m/s，k值又较大时，该处可能不适宜布置本文所选的风力发电机组，或应在满足安全性的前提下，选择更大叶轮直径机组，并在低风速区域尽量地提高风能利用系数，然而这种提高是有限的[16]。

5 结 论

(1)在研究范围内，平均风速一定的情况下，平均有效利用风功率密度系θ3μCp对于k值是一个减函数与增函数的乘积，其存在一个最大值。这个最大值对应的k值随着平均风速的变化而不同。

(2)平均风速较低的风场在资源评估时容易出现决策失误，故建议低风速风场的区分与决策不应简单通过平均风速或平均风功率密度来决定，而应同时结合k值来分析。

(3)在风电场建设的咨询、决策、设计等阶段，对拟建风电场内风能资源的平均能量风速系数θ和平均能量风速v能进行研究分析，可更准确地指导风电场的宏观选址、微观选址以及风力发电机组选型等工作。因此建议风力发电机组厂家在机组技术参数文件中增加针对该机组的k值与总体有效风能利用率的对应表。

[1]姚兴佳，王士荣，董丽萍.风力发电技术讲座(一)风力发电机组(1)[J].可再生能源，2006，127(3)：102-104.Yao Xingjia,Wang Shirong,Dong Liping.Lessons of status of wind power technology(Ⅲ) Wind power generator(1)[J].Renewable Energy,2006(3):102-104.

[2]张洋，刘雪枫，李强.风资源评估综述[J].水利电力机械，2007，29(5)：72-75.Zhang Yang, LiuXuefeng, LiQiang.Evaluation outline of wind resources[J].Water Conservancy & Electric Power Machinery,2007,29(5):72-75 .

[3]华泽嘉，闫少军，杨振华.风资源评估方法的研究[J].技术与市场，2012，19(11)：33-35.

[4]GB/T 18709—2002 风电场风能资源测量方法[S].

[5]GB/T 18710—2002风电场风能资源评估方法[S].

[6]王晓林.风功率密度等级划分和风能区划的修订建议[J].电力技术，2010，19(8)：78-82.Wang Xiaolin.Proposals of amendments of wind power density grade and wind energy area classification[J].Electric Power Technology, 2010, 19(8):78-82.

[7]朱德臣，汪建文.风工况双参数威布尔分布k值影响研究[J].太阳能，2007(6)：34-36.Zhu Dechen, Wang Jianwen.Study on the effects of k for two-parameter Weibull Distribution in wind resource assessment[J].Solar Energy,2007(6):34-36.

[8]杨振斌，朱瑞兆，薛桁.风电场风能资源评价两个新参数：相当风速、有功风功率密度[J].太阳能学报，2007，28(3)：248-251.Yang Zhenbin,Zhu Ruizhao,XueHeng.Two New Concepts on wind energy assessment in wind farm: equivalent wind speed, available wind power density[J].ActaEnergiae Solaris Sinica,2007,28(3):248-251.

[9]王承煦，张源.风力发电[M].北京：中国电力出版社，2002：31-47.

[10]宫靖远，贺德馨，孙如林，等.风电场工程技术手册[M].北京：机械工业出版社，2004：19-24.

[11]伯顿 T，等.风能技术[M].武鑫，等，译.北京：科学出版社，2007：12-34.

[12]李军，胡非，王丙兰，等.风速的Weibull分布参数[J].太阳能学报，2012，33(10)：1667-1671.Li Jun, Hu Fei, Wang Binglan, et al.Weibull parameters for wind speed[J].ActaEnergiae Solaris Sinica, 2012, 33(10):1667-1671.

[13]徐卫民，张星琳，孔新红.三种计算风速威布尔分布参数的比较[J].江西电力，2007,31(1):1-3.XuWeiming,Zhang Xinglin,Kong Xinhong.Comparison for three methods to calculate Weibull distribution parameters of wind speed[J].Jiangxi Electric Power,2007,31(1):1-3.

[14]胡燕平,甄海华,戴巨川.变桨距风力发电机额定风速的确定方法[J].太阳能学报，2011，32(3)：307-310.Hu Yanping,Zhen Haihua,Dai Juchuan.The study on the determining method for the nominal wind speed of pitch wind turbies[J].ActaEnergiae Solaris Sinica, 2011,32(3):307-310.

[15]高俊莹，徐建军，许爱华，等.风能利用系数模糊控制策略的研究[J].电气技术，2009(8)：36-42.GaoJunying,XuJianjun,XuAihui, et al.Study on fuzzy control strategy of wind energy utilization factor[J].Electrical Engineering,2009(8):36-42.

[16]邓英，张丹，周峰，等.提高风电机组风能转化效率的变速控制技术研究[J].电力与能源进展，2013，1(2)：64-71.Deng Ying, Zhang Dan, Zhou Feng, et al.Study to improve the wind energy conversion efficiency with the variable speed control[J].Advances in Energy and Power Engineering, 2013, 1(2):64-71.

(编辑：张小飞)

Energy Distribution Research Based on the ParameterkAnalysis of Two-Parameter Weibull Distribution Wind Conditions

JIANG Guangxu1, PAN Jingwen2, TIAN Jingkui1

(1.North China Power Engineering Co., Ltd.of China Power Engineering Consulting Group, Beijing 100120, China;2.Academy of Armored Forces Engineering of PLA, Beijing 100072, China)

Only by using the annual average wind speed and wind power density to determine the quality of wind energy resources is not comprehensive enough in wind resource analysis, which can not reflect the output capability of the wind resource.Investigating thekvalue，which is the shape parameter of two-parameter Weibull distribution wind conditions,is to find out its inherent relationship with the wind energy, wind speed distribution and wind energy distribution.And further research is put forward to find out the relationship between thekvalue and the effective wind energy utilization for differentCpcurves of wind turbine generators.The above research will supply a scientific guidance for wind resource assessment and wind turbine generator pre-selection during the consultation, decision-making, design and other stages of wind farm construction.

Weibull distribution; wind power; energy distribution; shape parameter

TM 614

A

1000-7229(2015)03-0105-04

10.3969/j.issn.1000-7229.2015.03.018

2014-09-04

2014-09-24

姜广绪(1983)，男，硕士，工程师，主要从事风力发电、太阳能光伏发电设计方面的研究工作；

潘晶雯(1984)，女，硕士，讲师，主要从事工程力学、材料力学方面的教学和研究工作；

田景奎(1960)，男，工学学士，教授级高级工程师，主要从事风力发电、太阳能光伏发电设计方面的研究和管理工作。