基于神经网络的磁流变减振器力学模型研究

张进秋，滕 涛，黄大山，姚 军

（装甲兵工程学院 装备试用与培训大队，北京100072）

随着磁流变技术的不断突破与发展，越来越多的基于磁流变技术的器件与设备研制成型，并在工程中得到应用．在结构振动控制领域，磁流变减振器以其出力大、体积小、响应快、结构简单、易与计算机结合实现智能化控制等优点［1］得到了科研人员的青睐，并在汽车减振［2］，军用武器系统［3］，土木工程［4］等领域已经有了具体的运用．

根据磁流变液在减振器中的受力状态和流动特点，可将MRD 分为剪切式、阀式、剪切阀式和挤压流动式［5］．剪切阀式磁流变减振器由于其设计简单、结构精巧等特点较为常用，并且已建立了多种阻尼特性模型，如Bingham 粘塑性模型，双粘塑性模型，双粘性滞后模型，Bouc－Wen模型等［6－8］．由于磁流变效应的复杂性，目前，还没有一种大家一致公认的精确性、适用性较高的力学计算模型．文献［9－11］采用了径向基（RBF）神经网络建立了磁流变减振器的力学模型，均取得了不错的效果．本文在此基础上，在神经网络模型参数辨识方面，改进了遗传算法中遗传算子和遗传机制的设定，以提高算法的全局搜索优化能力，使得参数辨识的精度能够满足实用性要求．

1 磁流变减振器的RBF神经网络力学模型

应用自行研制的MRF［12］，设计制作了最大阻尼力为300 N，构造如图1 所示的剪切阀式MRD，其基本参数如表1 所示．

图1 剪切阀式磁流变减振器Fig．1 Shear－valve mode MRD

表1 磁流变减振器的基本参数Tab．1 Basic parameters of MRD

图2 是试验得到的该减振器在加载幅值为10mm，频率为1 Hz正弦波时的位移－阻尼力曲线，由内至外的电流依次为0 A，0．5 A，1 A，1．5A，2．0A．由图2可知，阻尼力与位移、速度方向、控制电流有关，即

径向基函数（RBF）神经网络［13］是一种具有较强的输入－输出映射功能的三层静态前馈网络，其结构如图3 所示．它包括输入层、隐含层和输出层［14］．

输入层直接由信号源节点构成，其作用是接收输入信号并将其传递到隐含层．由式（1）可知，RBF神经网络的输入层具有3个节点，即

其中，n＝3．

图2 磁流变减振器位移－阻尼力曲线Fig．2 Displacement－damping force curve of MRD

图3 RBF神经网络结构图Fig．3 Structure of RBF neural network

隐含层节点由辐射状作用函数（径向基函数）构成，通常选取为高斯函数，当高斯函数的中心点（中心向量、中心宽度）确定以后，从输入层到隐含层的映射关系也就确定了，即

式中：C ＝［ck1ck2… ckn］为第k 个隐含层节点的中心向量；σk为第k 个隐含层节点的中心宽度．依据参考文献［14］，可确定RBF 神经网络隐含层的维数m，m ＝5．

输出层实现了对隐含层节点非线性函数输出的线性组合，由于本问题只涉及到一个输出——阻尼力，即l＝1，则有

式中：wk为第k 个隐含层节点到输出层的权重系数；θ为输出调节系数．

可建立磁流变减振器的RBF力学模型

磁流变减振器的RBF神经网络结构图如图4所示．

图4 磁流变减振器RBF神经网络结构图Fig．4 Structure of RBF neural network of MRD

2 遗传算法辨识RBF模型参数

RBF神经网络主要包含4类参数：中心向量c，中心宽度σ，输出权重w 和输出调节系数θ．合理、准确地辨识上述参数才可使得RBF 神经网络能够以任意需要的精度逼近待辨识网络．传统参数优化方法如牛顿法、最速下降法等，具有容易陷入局部极小、并且可能需要待辨识网络函数导数的信息等缺点．遗传算法［13］是基于遗传因子——染色体来模拟生物的进化，保留了适应度较高的染色体，将适应度差的染色体淘汰，并通过遗传算子产生新的染色体以保持染色体群的整体性，反复迭代，不断更新，以求得满足条件的染色体．采用遗传算法优化RBF 神经网络参数，克服了传统算法的缺点，并可以一次性完成多个RBF神经网络参数的辨识．

染色体编码方式．本文将上述4类参数统一编码至一条染色体中，即每条染色体都对应着一个可能的减振器力学模型．每个基因均以实数编码，并用浮点数来表示．由参考文献［15］可知，中心向量与中心宽度具有一定的相关性，对网络性能有很大的影响，采用中心向量和中心宽度交替排列的编排顺序，则染色体长度即为待优化参数的个数，如图5 所示．

染色体评价准则．定义训练样本的期望阻尼力F⌒与神经网络输出的阻尼力F 差的绝对值为训练样本的学习误差，有

图5 染色体编码Fig．5 Chromosome encoding

RBF神经网络参数优化的目标是使得上述学习误差最小，则可设定遗传算法适应度函数为

遗传算子设定．选择算子采用比例选择的方法，对种群中所有染色体的适应度进行累加得到适应度之和，M 为染色体的个数．建立各染色体在［0，S］上某区域之间的关联，染色体适应度越大，所占的区域越大，则被选择的几率越大．设定执行M 次上述选择策略，以使得染色体在更新过程中整体规模不变．交叉算子与变异算子的效率决定了染色体群进化的速度与程度．针对染色体群进化的特点，设定种群交叉概率与变异概率随着进化代数时变，即

式中：Pc为种群交叉概率；Pm为种群变异概率；t为进化代数；G 为最大进化代数．个体交叉概率与变异概率在群体概率的基础上随着适应度时变［15］，即

式中：Pci为个体交叉概率；Pmi为个体变异概率；为种群平均适应值；fiti为个体适应值．变概率的设定可以其在提高搜索效率的同时能够保持基因多样性，避免陷入局部最优．

遗传机制设定．首先采取存优策略将上一代最优的染色体保存到下一代中．其次进行变异判断，对于被选中采取变异措施的染色体，对适应度低的染色体采取高频变异以提高基因的多样性，对适应度高的染色体采取低频变异以进行有效的局部搜索［16］．再次进行交叉判断，对于被选中采取交叉措施的染色体，对适应度低的染色体采取高频交叉，对适应度高的染色体采取低频交叉，原理与变异算子相同．最后对于未被选中变异与交叉的染色体，将其与最优染色体混合，生成具有优良基因的新染色体遗传到下一代．

算法流程．依据上述算法的设计思想，给出了算法整体运行流程，如图6 所示．

图6 遗传算法流程图Fig．6 Flow diagram of genetic algorithm

3 实例验证

确定训练样本．以5组实验数据为基础，分别从0．5A，1A 和2A 条件下的曲线数据中各取出具有代表性的32个数据得到样本集合，即

式中：N＝96．

如图7 所示，所选择的样本基本能够表征减振器的力学特性．

图7 样本数据Fig．7 Sample data

遗传算法初始种群的大小为M ＝50，染色体长度为n×m＋m＋m＋l＝26．群体交叉概率系数pc1＝0．8，pc2＝0．5；群 体 变 异 概 率 系 数pm1＝0．6，pm3＝0．4；个体交叉概率系数pc3＝0．1，pc4＝10；个体变异概率系数pm3＝0．1，pm4＝80．依据96个训练样本运用遗传算法训练RBF神经网络，可得出减振器力学模型参数．

图8 给出了种群最佳适应度、平均适应度的进化趋势．由图8 可以看出，采取存优策略可以使种群中一直保存有进化过程中产生的最优的染色体，使得最佳适应度单调递增．由平均适应度可以看出，算法在进化过程中一直能够保持种群的多样性，避免陷入局部最优．

图8 最佳适应度和平均适应度的进化趋势Fig．8 Evolution tendency of best fitness and average fitness

图9 给出了磁流变减振器位移－阻尼力的实验样本点与通过神经网络模型计算得出的曲线的对比．通过计算可得出图中各点对应数据的相对误差的平均值为2．41%．表2 给出了部分数据的相对误差值．由表2 可以看出本文所建立的模型基本能够满足实用性的要求．

图9 神经网络模型计算数据与实验数据对比Fig．9 Comparison of computational data with experimental data

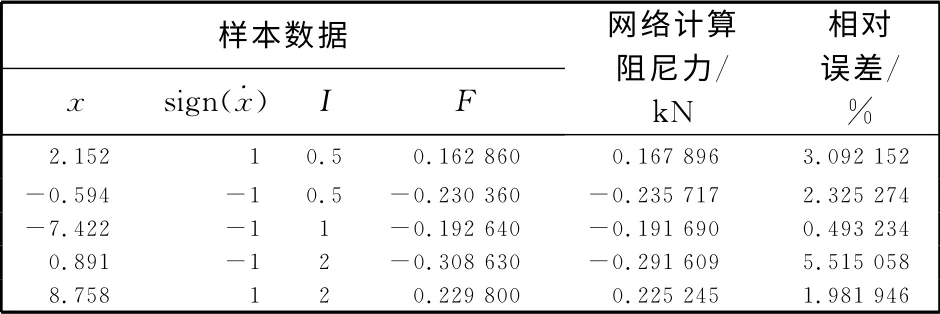
表2 部分神经网络计算数据的相对误差Tab．2 Relative error of computational data of partial neural network

4 结 论

本文建立了实验室自行设计研制的减振器的RBF神经网络模型，确定了网络输入层、隐含层和中间层的节点个数；运用遗传算法辨识RBF神经网络参数，确定了遗传算法的染色体编码方式、适应度函数，并改进了遗传算子与遗传机制；最后将优化得到的神经网络模型与原实验数据进行了对比分析，明确了本文所建模型的可行性和实用性，可为磁流变减振器的后续工作奠定基础．

本文所建立的模型还存在以下几点不足：

1）由于实验条件有限，没有测得减振器速度相关的数据，在模型中采用速度方向代替，可能会对参数辨识的精度有一定影响；

2）由参考文献［17］可知，激振频率和激振幅值对减振器输出的阻尼力影响较小，所以没有考虑激振频率和激振幅值对模型的影响，今后可以在此做出改进，以使模型更加精确；

3）模型参数不具有实际的物理意义，参数还不能够直接反映出减振器输出阻尼力的影响因素，这也限制了本模型的应用范围．

［1］熊超，郑坚，张进秋，等．磁流变阻尼器的设计及其力学特性实验研究［J］．军械工程学院学报，2004，16（2）：1－5．Xiong Chao，Zheng Jian，Zhang Jinqiu，et al．Design and characteristic study of magnetorheological fluid damper［J］．Journal of Ordnance Engineering College，2004，16（2）：1－5．（in Chinese）

［2］张进秋，王洪涛，冯占宗，等．车用双筒盘形缝隙式磁流变液减振器阻尼特性实验研究［J］．兵工学报，2009，30（11）：1488－1492．Zhang Jinqiu，Wang Hongtao，Feng Zhanzong，et al．Experimental study on damping characteristics of the twin－tube magneto rheological fluid damper with disc type orifice for the vehicle［J］．Acta Armamentarii，2009，30（11）：1488－1492．（in Chinese）

［3］高永强．基于磁流变减振器的履带车辆自适应悬挂系统研究［D］．北京：装甲兵工程学院，2012．

［4］汪志昊，陈政清．基于磁流变阻尼器的隔震高架桥Skyhook控制［J］．振动与冲击，2010，29（12）：196－199．Wang Zhihao，Chen Zhengqing．Skyhook control of isolated elevated highway bridge based onmagnetorheological（MR）damper［J］．Journal of Vibration and Shock，2010，29（12）：196－199．（in Chinese）

［5］欧进萍．结构振动控制——主动、半主动和智能控制［M］．北京：科学出版社，2003．

［6］Kwok N M，Ha Q P，Nguyen T H，et al．A novel hysteretic model for magnetorheological fluid dampers and parameter identification using particle swarm optimization［J］．Sensors and Actuators A，2006，132：441－451．

［7］Cesmeci S，Engin T．Modeling and testing of a fieldcontrollable magnetorheological fluid damper［J］．International Journal of Mechanical Sciences，2010，52：1036－1046．

［8］邓志党，高峰，刘献栋，等．磁流变阻尼器力学模型的研究现状［J］．振动与冲击，2006，25（3）：121－126．Deng Zhidang，Gao Feng，Liu Xiandong，et al．Stateof－art research on dynamical，models of magnetorheological damper［J］．Journal of Vibration and Shock，2006，25（3）：121－126．（in Chinese）

［9］徐健忠，王洪飞．基于神经网络的磁流变阻尼器逆控制研究［J］．机电工程，2009，26（3）：87－89．Xu Jianzhong，Wang Hongfei．Inverse control of MR damper based on neural network technology［J］．Mechanical ＆ Electrical Engineering，2009，26（3）：87－89．（in Chinese）

［10］涂建维，瞿伟廉，邹承明．MR 智能阻尼器试验研究及径向基网络模型［J］．武汉理工大学学报，2003，25（1）：43－45．Tu Jianwei，Qu Weilian，Zou Chengming．Test of MR damper and RBF network model［J］．Journal of Wuhan University of Technology，2003，25（1）：43－45．（in Chinese）

［11］Du Haiping，Lam James，Zhang Nong．Modelling of a magneto－rheological damper by evolving radial basis function networks［J］．Engineering Applications of Artificial Intelligence，2006，19：869－881．

［12］张建．磁流变液及其在半主动悬挂系统中的应用研究［D］．北京：装甲兵工程学院，2008．

［13］张国忠．智能控制系统及应用［M］．北京：中国电力出版社，2007．

［14］徐克虎，黄大山，王天召．基于RBF－GA 的坦克分队作战目标评估［J］．火力与指挥控制，2013，38（12）：83－87．Xu Kehu，Huang Dashan，Wang Tianzhao．Research on combat target evaluation of tank unit based on RBF－GA［J］．Fire Control ＆ Command Control，2013，38（12）：83－87．（in Chinese）

［15］李桂鑫．基于遗传算法的RBF 神经网络用于配电网线损计算［D］．天津：天津大学，2007．

［16］Xu Kehu，Huang Dashan，Wang Tianzhao．The application of improved genetic algorithm on weapontarget assignment［C］．Proceedings of 4th IHMSC，2012：311－313．

［17］束立红，王宇飞．磁流变阻尼器特性的实验研究［J］．噪声与振动控制，2010（3）：5－8．Shu Lihong，Wang Yufei．Experimental study on the performance of MR damper［J］．Noise and Vibration Control，2010（3）：5－8．（in Chinese）