基于电爆炸机理的被动电磁装甲板结构优化

苑希超，雷 彬，李治源

（军械工程学院 弹药工程系，河北 石家庄050003）

被动电磁装甲是一种利用电能来干扰和破坏来袭射弹的附加装甲，其主要作用机理包括磁流体不稳定性、电磁力以及电爆炸作用，是脉冲功率技术和电磁场理论在军事上的应用．

金属射流击穿被动电磁装甲板时，脉冲电容器组短路产生脉冲电流．欧姆加热效应使射流中迅速积累了大量的热能，金属射流在极短的时间内发生固→液→气→等离子体态的相变［1］．金属射流在由液态向气态转变的阶段发生电爆炸，形成绝缘的金属蒸气．金属射流的完整性被破坏，其侵彻能力大大降低［2－3］．电爆炸作用是被动电磁装甲作用机理中的重要部分，其作用主要受到比作用量的影响［2］．而在被动电磁装甲中，装甲板的结构直接影响到系统的电感，而电感的变化会改变系统的放电电流峰值和上升时间，同时装甲板间距的变化又影响到电流的作用时间．针对被动电磁装甲板的结构优化问题，陈少辉对电磁装甲各部分的电感进行了计算，并分析了电感变化对放电电流的影响［4］；同时，在作用时间模型的基础上，以最长作用时间为目标对装甲板间距进行了优化［5］，优化后的板间距可以使射流总的作用时间最长．但是，文章并没有考虑装甲板间距变化时对电路电感以及放电电流的影响，同时也没有考虑到电流的作用大小．卢聘对被动电磁装甲的电爆炸作用机理开展了进一步的研究［6－7］，并以比作用量的最大极大值为目标对装甲板间距进行了优化，在优化过程中考虑了间距变化对射流微元的比作用量的影响，优化后的板间距可以使射流微元受到的比作用量的极大值最大［3］．但是，在优化的过程中并没有考虑装甲板间距变化引起的电感变化，同时比作用量的最大极大值并不能准确地反映出电爆炸作用的效果．

本文考虑了装甲板结构参数变化对电感的影响，提出了采用爆炸比作为目标的装甲板结构优化方法，研究了源点距离和装甲板间距对射流爆炸比的影响，并对板间距和源点距离的关系进行了优化．

1 被动电磁装甲的比作用量模型

1．1 电路模型与基本假设

被动电磁装甲系统由脉冲电源以及连接在电源上的两块具有一定间隔的平行金属板组成．被动电磁装甲的基本结构如图1 所示．

图1 中C为电容器组；U 为电容器电压；L0和R0为系统电感和电阻，金属射流垂直侵彻装甲板；S0为虚拟源点到前装甲板之间的距离；d0为两个平行装甲板的间距．开关K 闭合，金属射流击穿被动电磁装甲板后，脉冲电容器组通过由射流和前、后装甲板以及连接线组成的回路放电产生高功率脉冲电流I．脉冲电流通过欧姆加热效应迅速在金属射流上积累大量的热能，使金属射流在极短的时间内发生电爆炸，金属射流的完整性被破坏，其侵彻能力大大降低［2－3］．

图1 被动电磁装甲结构示意图Fig．1 Basic structure of the PEA system

在电爆炸过程中，伴随着电阻的剧烈变化，但是在发生电爆炸之前，固态和液态阶段金属射流的电阻、电感变化相对较小［4，8］．将装甲板和金属射流的电阻表示为Rp和Ri，电感表示为LD和Li，并做如下假设：

1）金属射流的运动过程满足虚拟源点假设［9］．

2）电磁装甲板和金属射流质量均匀，射流垂直侵彻且接触良好，忽略被动电磁装甲板对射流速度的影响．

3）假定L0和R0为常数，而Rp，Ri以及Lp，Li只受装甲板间距和宽度以及侵彻位置的影响．

4）由于射流直径较细，忽略趋肤效应产生的影响，认为电流密度在射流中均匀分布．

射流头部接触后装甲板时脉冲电源开始放电，并以此作为零时刻进行分析，可以列出系统的电路方程

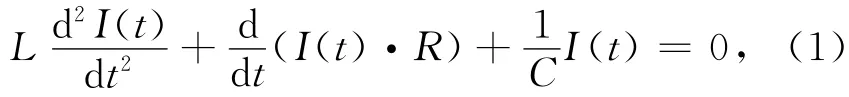
式中：L，C 和R 分别为回路电感、总电容和总电阻．求解得到系统的放电电流I（t）为［10］

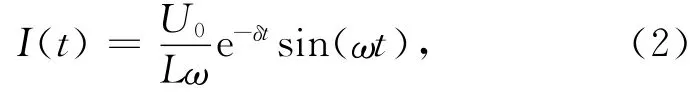
式中：U0为电容器组充电电压；衰减系数δ ＝R／2L；角频率

根据假设4）得到射流中的电流密度j（t），如式（3）所示．

式中：r 表示射流的半径．

1．2 比作用量模型

通常采用金属导体内积累的能量作为衡量金属射流能否发生电爆炸的一个重要指标，可采用比作用量进行表示［11］．其定义如下：

式中：h 为金属导体的比作用量；j（t）是电流密度；t1和t2分别为脉冲电流对金属导体作用的开始和结束时刻．

将金属射流划分为不同的速度微元，用vtip和vtail分别表示射流头部和尾部的运动速度．根据虚拟源点假设，对于图1 所示的电磁装甲结构中垂直侵彻的情况，开始放电的时刻t0＝（S0＋d0）／vtip．对于速度为v的射流微元，有

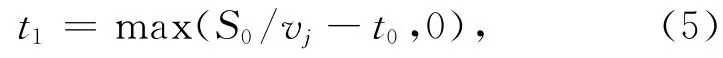
将式（3）代入式（4）可得到射流微元受到的比作用量值．

2 比作用量的影响因素分析

由1．2节分析可知，比作用量受到作用时间和电流密度的影响．对于固定速度梯度和固定半径的射流，其作用时间取决于装甲板的间距和源点的距离，电流密度则由电路参数决定；而根据1．1节的假设，影响电路参数的因素主要包括装甲板的间距以及装甲板的宽度．

2．1 板间距和板宽度对电路参数的影响

将两块平行的装甲板看成是平行的长方形金属导体，定义着弹点距离馈电一侧边缘的距离为装甲板长度．对于长度为a 的平行装甲板的电感可以近似地用式（7）表示

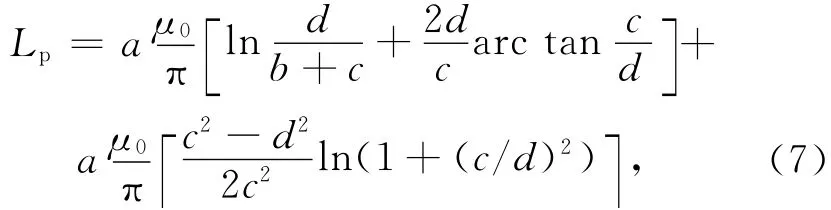
式中：b 为装甲板的厚度；c 为装甲板的宽度；d为两块装甲板间的距离；μ0为真空磁导率．

由式（7）可以看出，单位长度的装甲板电感受到装甲板厚度、宽度以及板间距的影响．电感随着装甲板厚度的增加而单调减小，而与装甲板宽度以及板间距的关系较为复杂．为直观地分析其关系，计算了固定厚度为6mm 时，不同装甲板的间距和宽度下的电感，结果如图2所示．从图2中可以看出，随着装甲板间距的减小和装甲板宽度的增加，装甲板电感均会变小．由式（7）可以看出，电感的大小与装甲板的间距和宽度的比值关系密切．因此，定义装甲板的间距和宽度的比值为装甲板的间宽比，进一步分析了间宽比与电感的关系，结果如图3 所示．

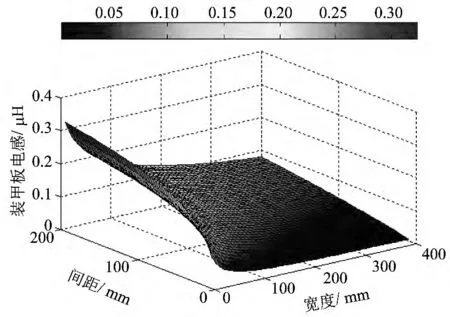
图2 不同宽度和间距时装甲板的电感Fig．2 Armor plate inductance under different widths and spaces

从图3 可以看出，随着间宽比的增加，装甲板的电感不断增加，但是电感变化的梯度随着间宽比的增大而减小，尤其是宽度相对于厚度大很多时，式（7）中的电感可以简化为关于间宽比d／c和长度a 的函数．

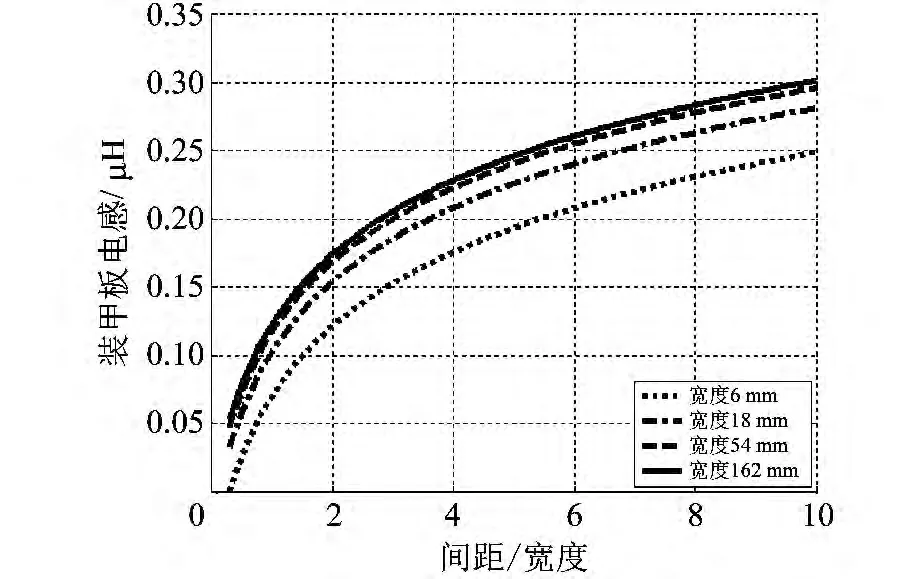
图3 装甲板电感随间宽比的变化Fig．3 Variation of armor plate inductance with the width－space ratio

因此，要减小装甲板的电感，可以从减小装甲板的长度和间距，增加装甲板的厚度和宽度几个方面加以考虑．

根据前面的假设，可以将金属射流看做一个均匀的细长圆柱铜导线，由于电流只流过两块装甲板之间的部分，因此按照短导线的电感公式，两块装甲板间的金属射流的电感计算公式可以近似表示为

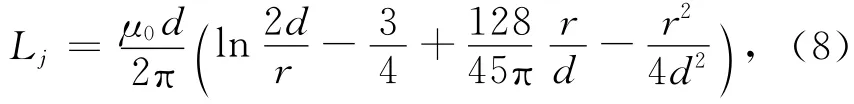
式中：d 为两装甲板间的距离；r为金属射流截面的半径．

图4 为不同半径和长度时射流的电感分布．从图中可以看出，射流电感随着长度的增加而增大，而随着半径的增大而减小．但是，由于射流半径的变化范围较小，所以，射流的电感主要由射流的长度即装甲板的间距所决定．

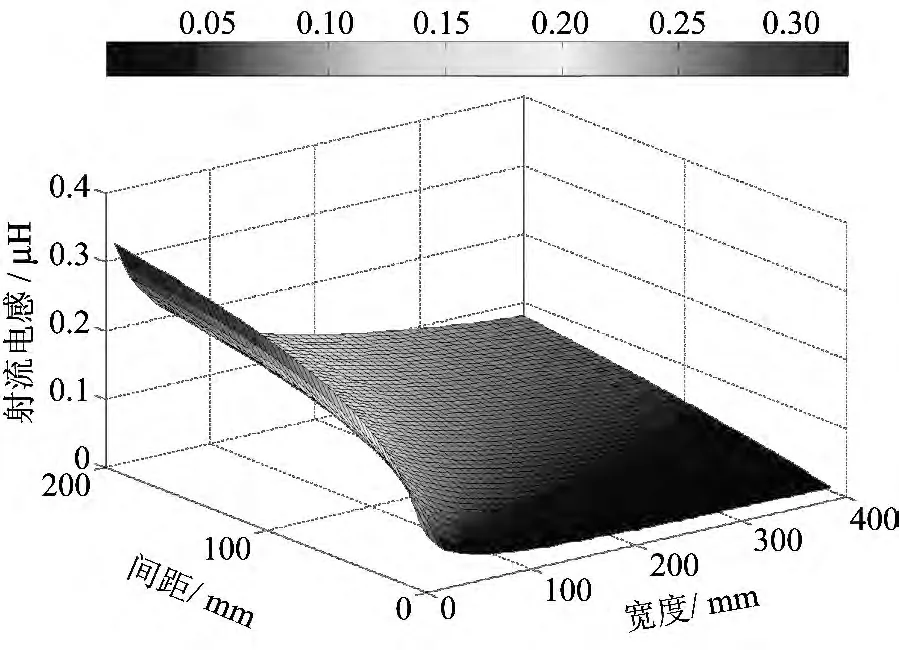
图4 不同半径和长度时射流的电感Fig．4 Jet inductance under different radiuses and lengths

2．2 板间距和源点距离对作用时间的影响

由式（5）和（6）可以看出，在射流速度梯度不变的情况下，射流微元的作用时间只和板间距d0和源点距离δ0有关．

图5 和图6 分别为S0＝200mm 时不同间距，d0＝80mm 时不同源点距离下计算得到的作用时间分布．从图5 可以看出，在间距较小时射流的总作用时间较长，而随着间距的增加，总作用时间逐渐减小；而各个速度微元的作用时间随着间距的增加而增大．但是，由于射流头部抵达后装甲板时才开始作用，尾部离开前装甲板时放电结束，所以随着间距的增大，头部和尾部不能受到完整电流作用部分的微元越来越多，即图中每条曲线底部和顶部的直线部分长度增加，作用时间又开始减小．

从图6 可以看出，在固定板间距的情况下，射流总作用时间随着源点距离的增加而增加，而由于源点距离增加后射流拉伸的长度会随之增加，所以射流头部和尾部附近的不完全作用的射流微元随着源点距离的增加而减少，即图中每条曲线底部和顶部的直线部分长度减小．

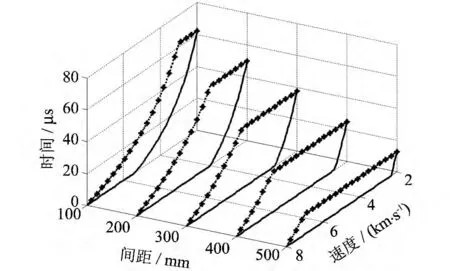
图5 不同间距时作用时间的分布Fig．5 Action time under different spaces

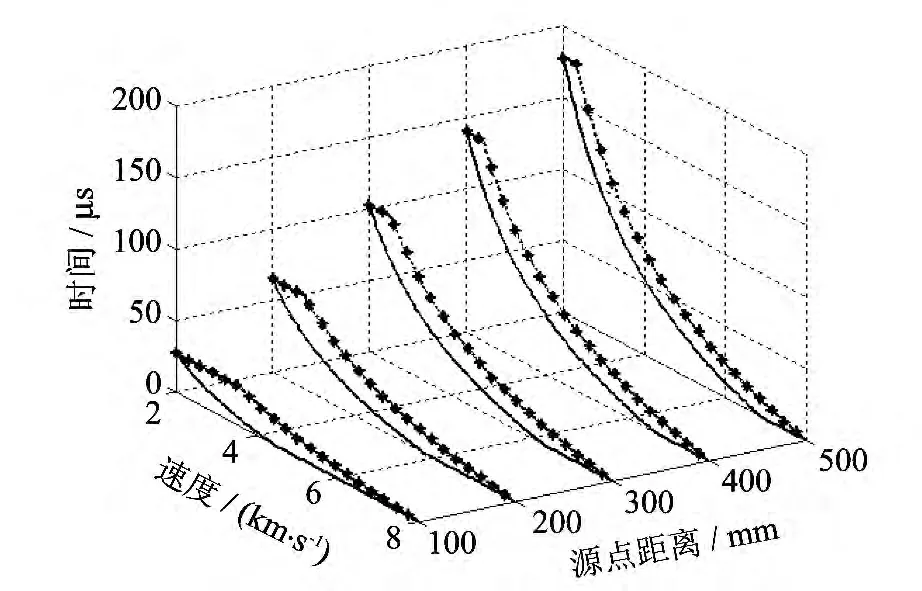
图6 不同源点距离时作用时间分布Fig．6 Action time under different source distances

2．3 板间距对比作用量的影响

射流微元受到的比作用量同时与电流密度和作用时间有关，结合式（3）～（8）可以计算出不同板间距和源点距离下的射流微元的比作用量．图7 给出了源点距离为200mm 时不同板间距下的比作用量分布，图8 给出了板间距为80mm 时不同源点距离下的比作用量．

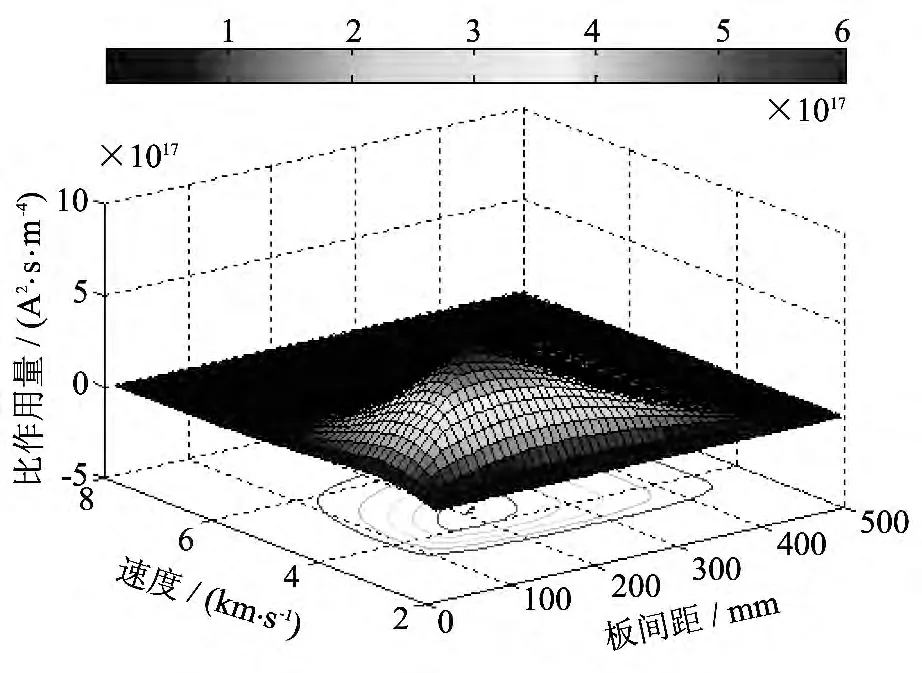
图7 不同板间距时射流微元的比作用量Fig．7 Specific action under different spaces

图8 不同源点距离时射流微元的比作用量Fig．8 Specific action under different source distances

从图7 中可以看出，射流的比作用量随着射流微元的速度不断变化，射流头部微元的比作用量小，而接近射流尾部的微元受到的比作用量大，并且受到了装甲板间距和源点距离的影响．

3 板间距的优化

普遍认为，在环境温度下导体发生电爆炸的比作用量阈值为1．7×1017A2·s·m－4［12］，因此，可以认为比作用量超过阈值的射流微元会发生电爆炸．定义发生爆炸的射流长度与总长度的比值为爆炸比α，用公式表示为

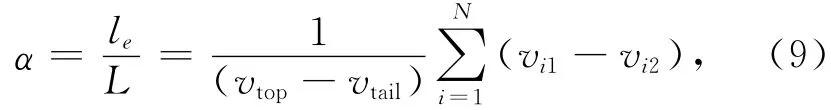
式中：le为发生爆炸的射流长度；L 为射流总长度；N 为发生电爆炸的射流的段数；vtop和vtail分别为射流头部和尾部的速度；vi1和vi2分别为第i段发生电爆炸的射流的上限速度和下限速度．不同板间距和源点距离时的爆炸比如图9 所示．

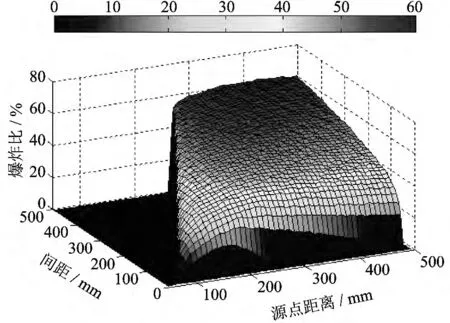
图9 不同板间距和源点距离下的爆炸比Fig．9 Explosion ratio under different plate spaces and source distances

从图9 中可以看出，对于不同的板间距，在源点距离达到某一值时爆炸比迅速达到最大，而随着源点距离的继续增大，爆炸比逐渐减小，但是变化非常缓慢；同时，对于固定的源点距离，随着装甲板间距的增加，爆炸比平缓地增加到最大值，但是随着板间距的进一步增大，爆炸比迅速降到最低．

图10 给出拟合得到的爆炸比分布脊线所对应的板间距和源点距离．从图中可以看出，两者分布基本服从线性关系．

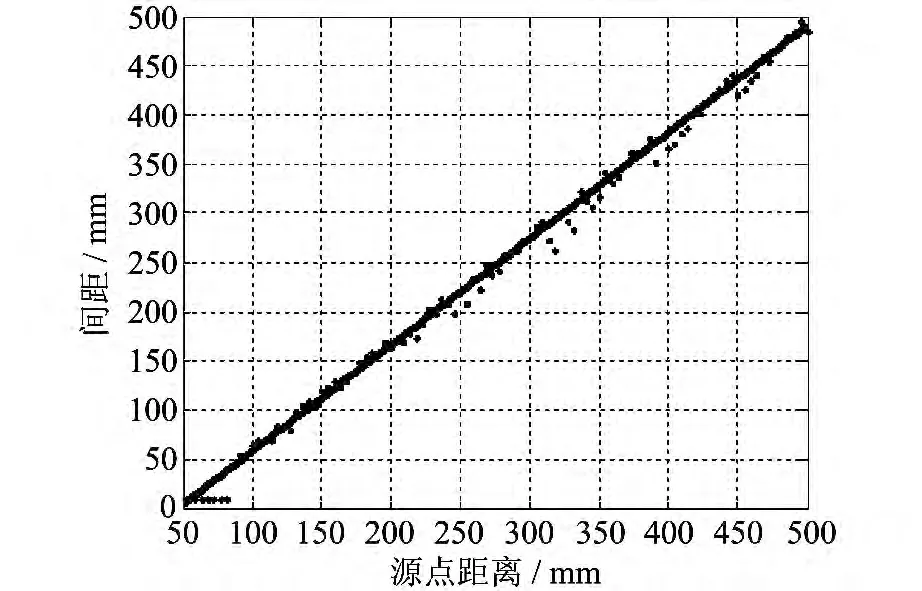
图10 爆炸比脊线坐标关系Fig．10 Relation of the explosion ratio coordinate of the crest line

采用比作用量的最大极大值作为优化指标，得到不同板间距和源点距离下射流受到的比作用量的最大极大值，如图11 所示．

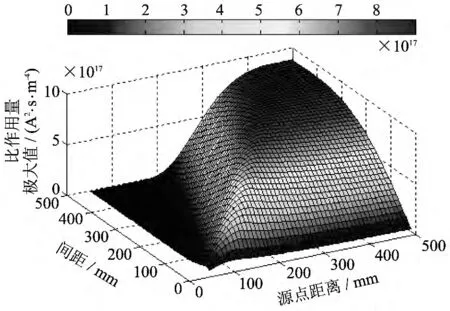
图11 不同板间距和源点距离下比作用量的极大值Fig．11 Maximum specific action under different plate spaces and source distances

从图11 中可以看出，不同板间距下的最大极大值随着源点距离的增加逐步增大，达到最大之后则变化十分缓慢；而在固定源点距离时，最大极大值随着板间距的增加出现先增加后减小的趋势．同样给出了拟合得到的比作用量极大值分布图脊线对应的板间距和源点距离的关系，如图12所示．从图12 中可以看出，两者的分布同样基本上服从线性关系．

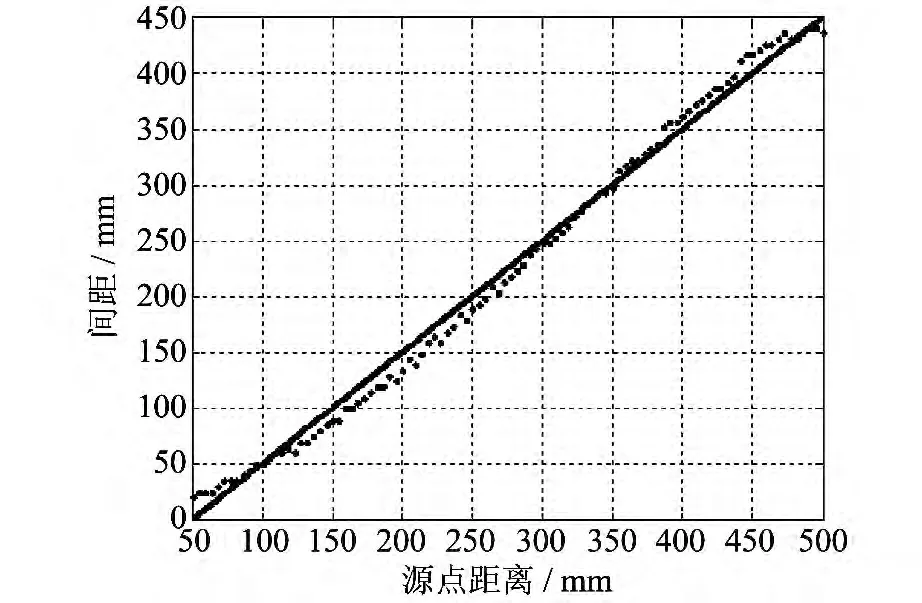
图12 比作用量极大值脊线坐标关系Fig．12 Relation of the maximum specific action coordinate of the crest line

与现有的优化分析相比，该方法考虑了板间距造成的电感变化，同时分析了最优源点距离和板间距的关系，具有更强的普遍性．

与比作用量最大极大值相比，采用爆炸比作为优化目标能够更准确地反应电爆炸对射流的破坏程度．从图9 和图11 的分析可以看出，采用爆炸比为标准得到的最优板间距略大于采用比作用量最大极大值得到的结果．但是，通过两者的定义可以看出，采用爆炸比作为目标的优化结果可以得到更加充分的爆炸长度，而以比作用量最大极大值为目标的优化结果只能保证射流中某电等够得到最充分的爆炸而不能兼顾整个射流．

4 结 论

本文基于被动电磁装甲的等效电路模型，分析了装甲板宽度和间距对系统电感的影响规律，结合作用时间模型研究了不同板间距和源点距离对射流微元作用时间的影响，得到了作用时间的变化规律，并进一步计算了比作用量的分布．分别讨论了板间距和源点距离单个量变化时比作用量的分布规律．最后分别通过爆炸比和比作用量的最大极大值两项指标对最优板间距与源点距离的关系进行了计算，得到了最优值所对应的板间距和源点距离的关系，为装甲板结构的优化设计提供了一定的参考依据．

［1］江壮贤，庄劲武，王晨，等．基于电磁斥力原理的高速触头机构仿真分析与设计［J］．电工技术学报，2011，26（8）：172－177．Jiang Zhuangxian，Zhuang Jinwu，Wang Chen，et al．Simulation analysis and design of a high speed contact mechanism based on electro－magnetic repulsion mechanism［J］．Transactions of China Electrotechnical Society，2011，26（8）：172－177．（in Chinese）

［2］Wickert M．Electric armor against shaped charges：analysis of jet distortion with respect to jet dynamics and current flow［J］．IEEE Transactions on Magnetics 2007，43（1）：426－429．

［3］李治源，卢聘，向红军，等．基于电爆炸机理的被动电磁装甲板间距优化分析［J］．装甲兵工程学院学报，2013，27（5）：52－56．Li Zhiyuan，Lu Pin，Xiang Hongjun，et al．Optimization analysis of passive electromagnetic armor plate spacing based on electro－explosive defense mechanism［J］．Journal of Academy of Armored Force Engineering，2013，27（5）：52－56．（in Chinese）

［4］陈少辉，雷彬，李治源．被动电磁装甲系统的电感参数分析［J］．装备环境工程，2010，7（5）：29－32．Chen Shaohui，Lei Bin，Li Zhiyuan．Analysis of inductance parameter in passive electromagnetic armor system［J］．Equipment Environmental Engineering，2010，7（5）：29－32．（in Chinese）

［5］陈少辉．被动电磁装甲对破甲弹的防护机理研究［D］．石家庄：军械工程学院，2011．

［6］卢聘，李治源，苑希超，等．被动电磁装甲电路特性的模拟试验［J］．装甲兵工程学院学报，2013，27（3）：66－69．Lu Pin，Li Zhiyuan，Yuan Xichao，et al．Simulation test on circuit characteristics of passive electromagnetic armor system［J］．Journal of Academy of Armored Force Engineering，2013，27（3）：66－69．（in Chinese）

［7］卢聘，李治源，吕庆敖，等．电感储能系统中电爆炸导体断路开关的电路特性研究［J］．兵器材料科学与工程，2013，36（5）：29－32．Lu Pin，Li Zhiyuan，LüQingao，et al．Circuit characteristics of electro－explosive opening switch used in inductive energy storage system［J］．Ordnance Material Science and Engineering，2013，36（5）：29－32．（in Chinese）

［8］苑希超，雷彬，李治源，等．被动电磁装甲对金属射流箍缩电磁力的计算及验证［J］．高电压技术，2013，39（1）：251－256．Yuan Xichao，Lei Bin，Li Zhiyuan，et al．Calculation and verification of pinch electromagnetic action on the shaped charge jet in the passive electromagnetic armor［J］．High Voltage Engineering，2013，39（1）：251－256．（in Chinese）

［9］Allison F E，Vitali R A．A new method of computing penetration variables for shaped－charge jets［R］．Maryland：Ballistic Research Laboratory，1963．

［10］雷彬，陈少辉，吕庆敖，等．被动电磁装甲对金属射流横向电磁力的计算及验证［J］．高电压技术，2011，37（10）：2569－2574．Lei Bin，Chen Shaohui，LüQingao，et al．Calculation and verification of lateral electromagnetic force on the shaped charge jet in the passive electromagnetic armor［J］．High Voltage Engineering，2011，37（10）：2569－2574．（in Chinese）

［11］Tucker T J，Toth R P．A computer code for the prediction of the behavior of electrical circuits containing exploding wire elements［R］．SAND－750041，1975：4－26．

［12］Appelgren P，Larsson A，Lundberg P，et al．Studies of electrically－exploded conductors for electric armour applications［C］．2nd Euro－Asian Pulsed Power Conference，Lithuania，Vilnius：2008：1072－1074．