噪声环境对弹上电子设备的作用机理研究

姚建军，余盛强，甄 瑞，闫红松

(北京自动化控制设备研究所，北京 100074)



噪声环境对弹上电子设备的作用机理研究

姚建军，余盛强，甄 瑞，闫红松

(北京自动化控制设备研究所，北京 100074)

建立了弹上电子设备声振耦合理论抽象模型，采用数值实验方法研究了电子设备周围环境的噪声载荷如何从外部传递到内部并对其内部器件的作用机理。分析得出：环境声场的声波入射到电子设备壳体外表面时发生反射与透射，其中反射声压与入射声压合成后同时作用于壳体外表面；合成压力载荷通过两条途径对电子设备器件内部产生影响，一条是激发电子设备壳体结构振动，并通过壳体结构及其与内部结构的机械连接，带动内部结构振动；另外一条是激发电子设备腔内声空间响应，产生二次声压场，再由二次声压场激励壳体内部结构产生振动；透射声压主要集中在低频且量级较小，其作用远比前述两条途径微弱。

噪声环境；电子设备；作用机理

0 引言

导弹等航天飞行器在发射飞行过程中，舱内电子设备会受到发动机推进系统诱发的低频(0～2000Hz)随机振动环境，以及气动噪声引起的宽频(10Hz～10kHz)声振激励环境影响。

对于亚声速导弹，噪声环境对舱内电子设备的影响远远弱于低频振动环境。但随着飞行速度的提高，特别是导弹再入大气层超高速飞行时，噪声的影响已非常显著。因此，在超声速/高超声速导弹用电子设备的研制中，噪声环境被明确列为与随机振动、冲击过载并驾齐驱的三大力学环境条件之一。与随机振动相比，噪声载荷的作用形式更加复杂、破坏性更为强烈。这一方面表现为作用频带更宽，另一方面表现在作用面积更大(注：随机振动只作用于电子设备与载体的机械连接部位，而噪声载荷则作用于电子设备的所有外露表面)。因此，传统的减振、隔振等结构动力学设计经验和方法，在解决噪声环境适应性问题时遇到了巨大的挑战。

本文工作的目的就是要剖析噪声载荷从电子设备的外部进入内部的传递途径、对内部器件产生破坏作用的机理，从而为弹上电子设备的噪声环境适应性设计提供理论依据和技术支撑。本文利用一个理论抽象的数值计算模型，采用对比分析数值实验的方法归纳出一般性结论。

从学科来讲，研究噪声环境对弹上电子设备的作用，是典型的声振耦合问题。它涉及流体力学、振动力学、弹性力学、计算力学、声学等。做为一门交叉学科，近年来越来越成为航空航天、车辆、船舶与舰艇等领域的研究热点，且各具有不同的研究重点。航空航天的研究重点是飞行器壳体结构、天线等面积和质量比较大的结构，在气动噪声、随机振动激励下的动力学响应计算。例如：Maahs利用有限元方法对STEREO 卫星的成像系统和高增益天线，在混响声场中的随机振动响应进行了计算；Cordioli等利用VA One 软件对航天器太阳翼和天线在混响声场中的加速度、位移、应力响应等进行了分析；韩增尧等利用有限元方法和统计能量分析方法，对卫星太阳翼噪声响应、整星高频随机振动进行了分析计算；王珺、张景绘等应用声学有限元+边界元分析软件Sysnoise，研究了飞行器仪器舱典型结构在随机振动+混响声场复合环境激励下的动力学响应；白长青等应用有限元软件ANSYS的谐响应分析功能研究了结构振动产生的空气声场，对航天器的理想化模型薄壁圆柱结构，研究了动力学响应的影响特性等。

车辆领域重点研究车室四周壁板的机械振动，与其内部声腔声振动的耦合特性、内饰材料对车室内部噪声场的影响、减振降噪设计等。这类研究中，通常将车身简化为带有弹性壁板的矩形封闭声腔，分析腔体的声振耦合模态、空腔内部的声压分布及其频响特性。这方面的研究文献较多，具有代表性的有：Kompella将汽车的各种振动与汽车内部噪声进行声固耦合分析，开创了汽车内部噪音控制研究的新局面；Nefske等对汽车内部的噪音控制模型进行了有限元研究，有效地预测了汽车内部的声学特性；戴扬、陈藻等研究了具有弹性壁面的矩形封闭空腔中，壁板振动模态与空间声模态的耦合特性；邓兆祥、曹友强等研究了结构声腔耦合系统频率耦合机理以及声固耦合系统在发动机和路面激励作用下的车内声学响应。

舰艇与船舶领域重点研究弹性壳体结构在湍流边界层，脉动压力作用下的受激振动、壳体结构振动、外场声辐射的特性和规律，以及水下隐身设计等，这方面的研究文献也相对较多。

本文采用载荷传递路径分析方法来探讨研究声振耦合问题。主要内容不仅包括当前航空航天领域重点关注的壳体结构在噪声激励下的动力学响应计算，也不仅包括当前车辆领域重点关注的车室四周壁板的机械振动与其内部声腔声振动的耦合特性和当前船舶领域重点关注的机械振动产生的声辐射等，而且还包括被激发起来的结构应力场、腔内声场与内部结构的耦合特性，以及内部结构的响应特性计算等。

载荷传递路径分析方法研究声振耦合问题，是对当前声振耦合理论应用的进一步拓展，鲜有人涉及，因而相关研究文献亦极少。

1 模型的建立

弹上电子设备一般为一长方体盒式结构。盒子为其主体框架，起防护和机械连接作用，电子功能模块安装在盒子内部。这里，参照声学领域通常用来研究结构机械振动与声腔声振动耦合特性所使用的经典方法，建立一个具有N(N=1,2,3,4,5,6)个弹性壁面的矩形空腔理论抽象模型(其中一个壁面为弹性板，其他五个壁面为刚性板)。在该模型中，如果将腔体的一个壁面当成是弹上电子设备的盒式壳体，环境噪声载荷作用在壁的外表面，与其相对的另一个壁面当成安装于壳体内部的功能部件结构。其余四个壁面则为壳体与内部结构之间的机械连接，空腔等效于壳体与内部模块结构之间的空气间隙。壳体与内部结构之间既通过机械连接又通过空气连接，同时包含了电子设备的结构动力学特性和内部声学特性。

在该模型中，无论是矩形壁板还是矩形空腔都存在规则的解析模态解，便于对结果进行分析，且由于实际结构的复杂模态可看成是基本规则模态的合成，所以认为该模型是对弹上电子设备声振耦合特性的理论抽象。模型的几何形状虽然为方形，但从模态分析的角度，可看成是其他任意复杂形状的基元特征，因此认为该模型不仅具有特殊性而且还具有一般性。

图1 实体模型图Fig.1 Solid model

所建立的矩形封闭空腔实体模型的外形尺寸与弹上电子设备的典型外形尺寸相当，取为200mm×240mm×160mm，腔体壁厚5mm，如图1所示；腔体材料为铝，其弹性模量E=70GPa、泊松比μ=0.33、密度ρ=2700kg/m3、结构阻尼损耗因子η=0.02，体纵波声速cs=6260m/s；腔体内外气体环境均为一个大气压、20℃条件下的空气，密度ρ0=1.21kg/m3，声速c0=344m/s。在ANSYS15.0软件环境下建立其有限元模型并完成计算。其中，腔壁采用六面体高阶结构单元SOLID186来划分网格，腔内空气采用六面体高阶流体单元FLUID220来划分网格，在流体网格与结构网格的交界上，利用FSI界面载荷将结构运动与流体压力耦合在一起。

计算得到，该模型在完全固定腔体的上下左右四个外表面，前/后壁板(注：法线与X轴平行的壁板)的第一阶纯结构振动频率为1397Hz；腔内声空间的(1,0,0)、(2,0,0)、(3,0,0)简正模态频率分别为903Hz、1805Hz，2710Hz。

图2 用开缝代替密封不严的实体模型图Fig.2 non-airproofed solid model with apertures

2 数值实验方案的确定

对于上面建立的理论抽象数值模型，可以通过对前壁板、除前壁板以外的其他壁板、空腔、腔体的机械约束等进行不同方式的处理来达到不同的实验目的。例如，将前壁板处理成结构体或非结构体(只是作为声学介质)，可以对比分析结构的动力学特性对噪声载荷传递的影响；在前壁板上开缝或不开缝，可以对比分析腔体结构的密封性能对噪声载荷传递的影响；将除前壁板以外的其他壁板处理成空气介质或非空气介质，可以对比分析声学腔体对噪声载荷传递的影响；将空腔充满空气或抽成真空，可以对比分析气体介质对噪声载荷传递的影响；对腔体机械约束的不同方式，代表了前后壁板之间不同程度的机械连接关系，可以对比分析机械连接对噪声载荷传递的影响。将这些不同的处理方式进行组合形成不同的数值实验方案，见表1。对于每种实验方案，所施加的环境噪声条件是一致的，即，令声压级为160dB的单频各向均匀声场从前壁板的左侧入射(假设壁面无限大，声波不能衍射到壁板后面)，入射波的频率从50～3000Hz变化，每隔10Hz进行一次简谐响应计算。对实验结果的提取可分为两种情况，对于纯声学计算，主要观察噪声载荷穿过前壁板后的声压变化情况；对于声振耦合计算，还要观察前后壁板中央位置处的加速度响应。

表1 数值实验方案列表Tab.1 Numerical experiment schemes

3 实验结果分析

图3 第一方案下，前壁板后靠近板中央位置处的声压随频率变化曲线Fig.3 Scheme 1: the curve of acoustic pressure near front wall with frequence

图4 第一方案下，前壁板后中心线上的声压随位置变化曲线Fig.4 Scheme 1: the curve of acoustic pressure behind front wall center with position

图5 第二方案下，腔内靠近前后壁板中央位置处的声压随频率变化曲线Fig.5 Scheme 2: the curve of acoustic pressure near front wall with frequence

图6 第二方案下，前壁板后中心线上的声压随位置变化曲线Fig.6 Scheme 2: the curve of acoustic pressure behind front wall center with position

图7 第三方案下，腔内靠近前后壁板中央位置处的声压随频率变化曲线Fig.7 Scheme 3: the curve of acoustic pressure near front wall with frequence

图8 第三方案下，前壁板后中心线上的声压随位置变化曲线Fig.8 Scheme 3: the curve of acoustic pressure behind front wall center with position

图9 第四方案下，腔内靠近前后壁板中央位置处的声压随频率变化曲线Fig.9 Scheme 4: the curve of acoustic pressure near front wall with frequence

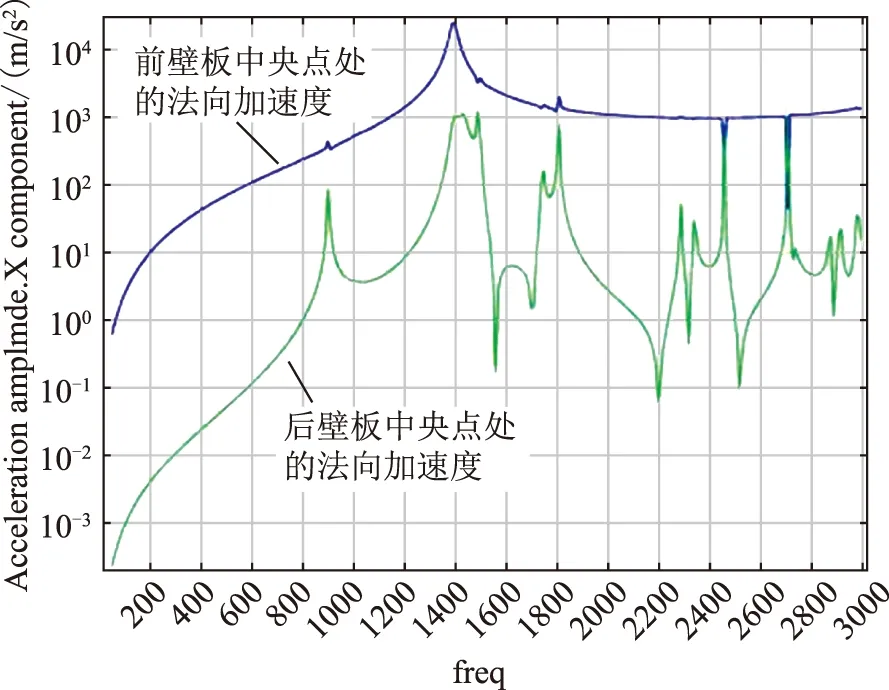
图10 第四方案下，前后壁板中央点处的加速度响应随频率变化曲线Fig.10 Scheme 4: acceleration swing at front /black wall center point with frequence

图11 第五方案下，前后壁板中央点处的加速度响应随频率变化曲线Fig.11 Scheme 5: acceleration swing at front /black wall center point with frequence

图12 第六方案下，前后壁板中央点处的加速度响应随频率变化曲线Fig.12 Scheme 6: acceleration swing at front /black wall center point with frequence

图13 第七方案下，腔内靠近前后壁板中央位置处的声压随频率变化曲线Fig.13 Scheme 7: the curve of acoustic pressure near front wall with frequence

图14 第七方案下，前后壁板中央点处的加速度响应随频率变化曲线Fig.14 Scheme7: acceleration swing at front /black wall center point with frequence

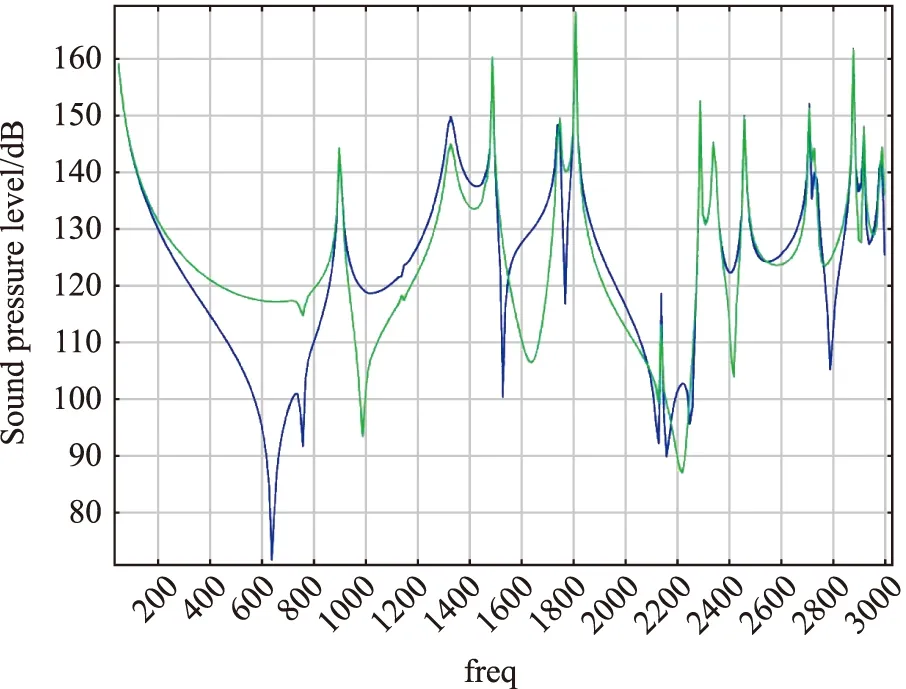
图15 第八方案下，腔内靠近前后壁板中央位置处的声压随频率变化曲线Fig.15 Scheme 8: the curve of acoustic pressure near front wall with frequence

图3～图16所示分别为依据各实验方案得到的数值实验结果。

图16 第八方案下，前后壁板中央点处的加速度响应随频率变化曲线Fig.16 Scheme8: acceleration swing at front /black wall center point with frequence

由图3、图4可以看出，入射声波穿过薄壁铝介质后的透射声压随频率近似呈指数规律衰减，200Hz以后减弱到130dB以下，板后声压处处相等，不产生波动。

由图5、图6可以看出，入射声波穿过薄壁铝介质进入封闭腔体内部的透射声压不论是频率分布还是空间分布，都与实验方案一进入自由开放空间的情形存在显著不同：在低于200Hz的低频段，透射声压随频率的衰减规律及空间分布与实验方案一基本一致。但在200Hz以上的几个特殊频率点(注：为腔内声空间的简正频率)附近，透射声压随频率急剧增大后又急剧衰落，出现尖峰，其幅值远大于实验方案一自由开放空间下，相同频率附近的声压幅值，即：透射声压在腔内出现频率选择性二次放大；这些选择性放大的声压在腔内的分布呈现出很规则的驻波曲线；受这些选择性二次放大波的影响，其他频率处的透射声压也没能得到充分衰减。

由图7、图8可以看出，由于结构体的振动，壁板的隔声性能发生了显著变化，与实验方案一自由开放空间下的规律甚至相反：透射声压在低频处显著衰减，随频率升高而逐渐增大，在某个特殊频率点处(注：为壁板结构的第一阶固有频率)达到极大值后又逐渐衰减，但其幅值仍然高于在实验方案一自由开放空间下的情形，这时的弹性壁板类似一个高通滤波器，壁板后面的声压是滤波后的穿透声压与结构振动辐射声压的合成。

由图9可以看出，入射声波穿过弹性壁板进入封闭空腔后的声压频响分布情况，兼具实验方案二声波透入封闭空腔内的频响特性与实验方案三声波穿过自由开放空间弹性壁板结构后的频响特性。即：透射声压在低频处显著衰减，在几个特殊频率点处出现频率选择性二次放大；受其影响，这些峰值频率点附近频率处的声压也没能得到充分衰减；除此而外，还增加了一些弹性壁板与封闭空腔耦合后引起的新特征，如位于2200～2600Hz之间三个尖峰点处的峰值比实验方案二单纯封闭空腔时的明显增大。

由图10可以看出，入射声波不仅引起前壁板振动而且还引起后壁板振动；前壁板振动的峰值频率只发生在前壁板结构固有振动频率点处，腔内声压对其影响甚弱，只是在相应频率点处出现了一些微不足道的毛刺；后壁板振动则主要受腔内声压的影响，其加速度响应峰值频率几乎与图9中腔内声压的峰值频率一一对应。

由图11可以看出，在腔内没有声波传播的介质即腔内没有声压时，前壁板结构的振动几乎不受影响，而后壁板结构则几乎不会发生振动，即在这种约束情况下，前壁板几乎不能直接通过固体结构带动后壁板振动，后壁板的振动主要是由腔内声压引起的。

与实验方案四结合起来看，说明声波透入带有弹性壁板的封闭空腔后产生的声压，能够引起腔内结构产生非常显著的振动。即外界环境噪声引起封闭腔体内部结构的动力学响应不容忽视。

由图12可以看出，噪声载荷激发前壁板振动，前壁板通过壳体结构带动后壁板也产生同样剧烈的振动。

对比图13与图9可以看出，结构约束状态改变后，腔内声压峰值的频率几乎没有改变，只是其峰值稍有变化。这说明壳体与腔体的耦合作用程度发生改变。对比图14与图12可以看出，在腔内充满空气时，纯粹由结构振动传递引起的后壁板的加速度频率响应曲线上增加了几条毛刺，毛刺出现的频率与图13所示腔内声压峰值出现的频率一致。这说明后壁板的振动是由壳体结构振动与腔内声压波动共同引起的。至于哪个是主要因素哪个是次要因素，则随着具体结构形式及腔体形状不同而异，不能一概而论。在本例中，显然壳体结构振动是引起后壁板振动的主要因素。

对比图15与图9可以看出，由于微小缝隙使得壳体泄露后，腔内声空间的声压在高频处的峰值分布几乎没有变化，只是部分频率点处的峰值有所增加。但在低频区域，这个微小的缝隙却严重破坏了壳体结构对入射声波的高通低阻滤波功能，使得低频声波显著地透入腔内。

对比图16与图10可以看出，尽管缝隙使得腔内的低频声压显著增强，但由于其频率远低于后壁板结构的固有频率，所以对后壁板的振动响应没有造成太大影响。反而使得后壁板在某些高频点处的响应减小，这主要是由于缝隙处的能量泄露减弱了腔内声场与后壁板结构的耦合作用程度。在实际工程中，由于密封不严而产生的缝隙对腔体内外气体流通的阻滞程度远远大于该计算模型所设置缝隙的作用，所以认为，壳体的密封质量，对弹上电子设备在噪声作用下的振动响应没有太大影响。

4 结论

根据上面的分析，可以对环境噪声载荷从电子设备外部传递到内部，对其内部器件作用的机理形成如下认识：

1)环境声场的声波入射到电子设备壳体外表面时发生反射与透射。其中反射声压与入射声压合成后，同时作用于壳体外表面。

2)合成压力载荷通过两条途径对电子设备内部器件产生影响：一条是激发壳体结构振动，并通过壳体结构及其与内部结构的机械连接，带动内部结构振动；另外一条是激发腔内声空间响应产生二次声压场，再由二次声压场激励壳体内部结构产生振动。即，一条为机械结构连接路径，另一条为气体介质连接路径。

3)环境噪声透过壳体后的透射声压主要集中在低频，量级较小，对内部器件的作用远比通过2)中所述两条途径产生的作用微弱。

4)类似密封不严等因素造成的壳体内部腔体与外界的微通道对弹上电子设备在噪声作用下的振动响应没有显著影响。

[1] Maahs G. Acoustic test and analysis[C]//. The 2007 S/C & L/V Dynamic Environments Workshop, EI Segundo, USA，2007.

[2] Cordioli J, Gardner B, Pattison G. Prediction of dynamic stresses and forces in space structures from random acoustic excitations[C]//. The 2008 S/C & L/V Dynamic Environments Workshop, EI Segundo, USA, 2008.

[3] 韩增尧, 曲广吉. 统计能量分析在太阳翼噪声分析上的应用[J].中国空间科学技术, 2001, 21(2): 52-56.

[4] 王珺，张景绘，宁玮. 复合环境激励下的声振耦合分析[J].振动与冲击，2011,30(2)：15-18.

[5] 白长青，周进雄，闫桂荣. 声振耦合对薄壁圆柱结构动力特性的影响[J].机械工程学报，2011,47(5)：78-84.

[6] Kompella M S．Variation of structural-acoustic characteristics of automotive&vehicle[J].Noise Control Engineering Journal，1996，44(2)：93-99.

[7] Nesfke D J，Sung S H．Vehicle interior acoustic design using finite element methods[J].Journal of Vehicle Design，1995，6：24-40.

[8] 戴扬，陈藻. 振动模态与声模态的耦合特性分析[J].振动工程学报，1992,5(2)：98-103.

[9] 邓兆祥，高书娜.结构声腔耦合系统频率耦合机理探讨[J].振动与冲击，2012,31(14).

[10] 曹友强，邓兆祥,等. 车内耦合声场振动噪声预测研究[J]. 汽车工程，2008,30(6)：484-487.

Study on Action Mechanism of Noise Environment on Missile-borne Electronic Equipments

YAO Jian-jun, YU Sheng-qiang, ZHEN Rui, YAN Hong-song

(Beijing Institute of Automatic Control Equipment,Beijing 100074, China)

A vibro-acoustic coupled principle model is presented, and how the noise loads transfer from exterior of electronic equipments into interior and act on electronic components is researched by means of numerical experiments. Some conclusions obtained are those: the incidence acoustic wave arises reflection and refraction on the exterior surfaces of electronic equipments, and the synthesized acoustic pressure of incidence acoustic wave and reflection acoustic wave acts on them and makes effects on the interior electronic components by two ways, one is forcing the frame of electronic equipments to vibrate. then exciting the electronic components to vibrate via mechanism link, the other is exciting the interior sound field, then forcing the electronic components to vibrate. The less refraction acoustic pressure focuses mainly in lower frequency region, and the action is negligible.

Noise environment; Electronic equipment; Action mechanism

2015 - 03 - 15；

2015 - 04 - 20。

姚建军(1974 - )，男，研究员，主要从事多物理场仿真分析与结构功能一体化设计方面的研究。

E-mail：yjjnl@sina.com

V414

A

2095-8110(2015)03-0120-08