基于UKF的GPS/SINS组合导航直接式滤波算法

王 林，林雪原

(1.海军航空工程学院 研究生管理大队，山东 烟台 264000；2.信息融合研究所，山东 烟台 264000)



基于UKF的GPS/SINS组合导航直接式滤波算法

王 林1，林雪原2

(1.海军航空工程学院 研究生管理大队，山东 烟台 264000；2.信息融合研究所，山东 烟台 264000)

基于无迹卡尔曼滤波(UKF)方法，使用姿态、速度、位置等9个导航参数组成状态向量，以GPS系统输出的速度、位置组成6维观测向量，构建直接式结构的UKF滤波器。该滤波器能够直接反映系统导航参数的动态过程，准确显示运动状态演变。针对GPS/SINS组合导航系统的特点，构建了GPS/SINS组合导航直接式卡尔曼滤波仿真验证系统，仿真结果验证了基于UKF的GPS/SINS组合导航直接式滤波算法的有效性，该直接式非线性滤波算法可使惯性组合导航系统的导航精度得到提高。

惯性组合导航；无迹卡尔曼滤波；直接式滤波

0 引言

卡尔曼滤波是一种基于模型的线性最小方差估计，其标准离散型算法具有递推计算、使用计算机执行、适用于平稳或非平稳多维随机信号估计等独特优点。所以在随机信号处理中，特别是在组合导航设计中应用广泛。根据卡尔曼滤波方法设计的组合导航滤波器，成为组合导航系统的核心。标准卡尔曼滤波只适用于系统方程和量测均为线性时的估计，但是工程实践中所遇到的物理系统数学模型往往是非线性的，即系统方程是非线性的，或者系统和量测都是非线性的。尽管扩展卡尔曼滤波(EKF)可解决系统和量测为非线性时的估计，但必须用泰勒级数的方法对原系统和量测作展开并舍去非线性项，再用基础卡尔曼滤波算法对处理后的系统和量测方程作滤波计算，可见EKF本质上仍然是基础卡尔曼滤波。由于在线性化处理过程中舍弃了非线性的高阶项，EKF只适用于滤波对象非线性较弱的情况下，被估计对象非线性性质越强，所产生的误差就会越大，严重的会引起滤波发散[1-2]。

为了解决强非线性条件下的估计问题，出现了基于UT变换的UKF算法，为以直接式滤波方法解决强非线性条件下的惯性组合导航提供了契机。

本文将UKF应用于组合导航，建立惯性组合导航系统的直接式滤波模型，以导航参数作为状态变量，以GPS系统的速度和位置组成观测向量，实现直接式滤波关键计算流程，以微小型飞行器作为对象进行仿真验证。

1 UKF滤波算法

UKF和标准卡尔曼滤波都是线性的最小方差估计，都是建立在模型基础上的算法，两者的不同点在于计算最佳增益阵的方法。标准卡尔曼滤波在计算最佳增益阵时，建立在系统方程和量测方程均为线性的基础上。而UKF在最佳增益阵的计算中，对系统方程以及量测方程的性质没有任何具体的约束，所以UKF算法既可以在线性条件下使用，也可以在非线性条件下使用[2]。

设系统方程和量测方程为：

(1)

其中k-1,k表示离散时刻，Xk为状态预测，Xk-1为上一时刻的状态估计，其方差为Pk-1，uk-1为系统确定性控制项，Wk-1为系统噪声，其方差为Qk-1，Zk为量测值，Vk为量测噪声，其方差为Rk，系统和量测噪声均服从高斯分布。UKF滤波要解决的问题是在已知状态初始值X0，系统确定性控制序列u0,u1,…,uk-1以及量测值序列Z1,Z2,…,Zk的情况下，估计系统的状态变量Xk。

UKF采用递推计算方式，主要包括两个过程：状态预测计算和修正计算。已知状态变量的维数为n，UKF用UT变换的方式获取2n+1个采样点(sigma点)，实现状态及其相关统计量的递推计算。在k时刻，2n+1个对称的采样sigma点及各点对应的权值为[1-2]:

(2)

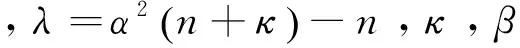
UKF算法的核心是UT变换，它能够产生代表状态量统计特性的最少数量的采样点，具有一些比较好的特性：UKF方法中的状态变量传递过程中通过的是没有被近似处理的系统，精度较高，模型较精确；UKF在保证精度的条件下，其计算量相比粒子滤波(PF)要少很多。这些特点使得UKF成为一种重要的非线性滤波技术[1]。

2 基于UKF的惯性组合导航直接式滤波模型

基于标准卡尔曼滤波及扩展卡尔曼滤波的间接式组合导航系统，使用线性化的惯性组合导航系统的误差方程作为状态方程，以惯性组合导航系统的误差作为被估状态。而基于UKF的GPS/SINS组合导航直接式滤波则以捷联惯性导航系统的机械编排方程作为状态方程，直接使用导航参数做被估状态，是一种直接式滤波方法，状态方程及量测方程无需线性化。

2.1 状态方程与量测方程

采用“东北天”地理坐标系作为导航坐标系，惯性导航系统采用指北方位机械编排，状态方程如式(3)所示。

(3)

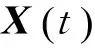
(4)

滤波过程中，噪声进入非线性系统中，参与系统状态转移，所以如式(4)所示将系统噪声和量测噪声与状态向量一起组成增广向量Xa，增广向量维数n为21，增广的方差阵为Pa。

状态方程依据惯性导航系统工作原理展开式如式(5)所示。

(5)

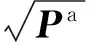
基于UKF的直接式卡尔曼滤波的观测方程直接反映观测系统的量测原理，以GPS输出的速度和位置作为观测量，量测方程为式(6)所示，V为量测噪声。

(6)

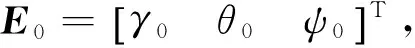
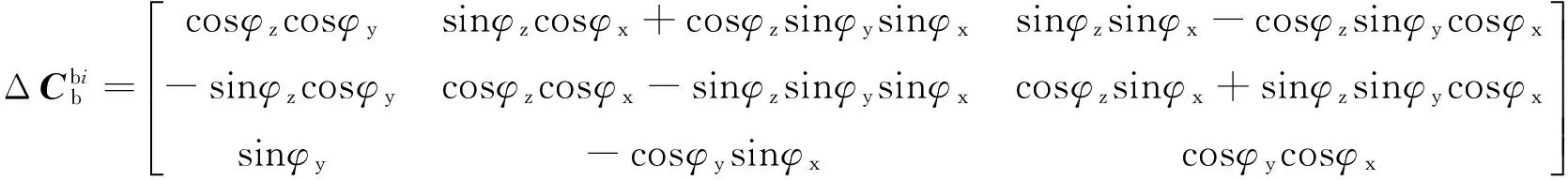
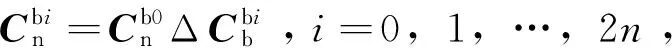
2.3 基于UKF的惯性组合导航直接式滤波流程

基于UKF的惯性组合导航直接式滤波系统以状态向量、系统噪声与量测噪声组成增广向量，以GPS输出的速度和位置作为观测量，其滤波流程分为三个部分：初始化及样本点计算、时间更新、状态更新。

2.3.1 初始化及样本点计算

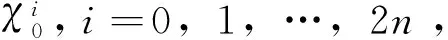
2.3.2 时间更新

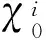
2.3.3 状态更新

获得测量值及预测值后，进行新息计算，通过滤波增益矩阵，得到每个状态对应的误差修正量，UKF中新息及滤波增益的计算都使用到对状态预测点集、测量预测点集均值和方差的计算。

通过sigma点集得到的状态预测均值和方差为

估计观测值的均值和方差为

计算状态预测与量测估计的协方差为

计算滤波增益

通过增益矩阵，获得各个状态的误差修正量，状态和方差更新为

3 基于UKF的惯性组合导航直接式滤波仿真验证

以微小型飞行器作为使用载体构建图1所示的滤波仿真验证系统，采用飞行器动态仿真和真实的导航传感器测量误差数据合并生成动态数据的方法，惯性元件和GPS误差数据从实验室实际测试的数据中注入。飞行轨迹按微小型飞行器性能特点及使用需求设定，包括如下过程：加速—爬升—平直飞行—爬升—平直飞行—转弯—平直飞行—再一次爬升—平直飞行—转弯—下滑—盘旋状态，如图2。仿真时间为3600s。

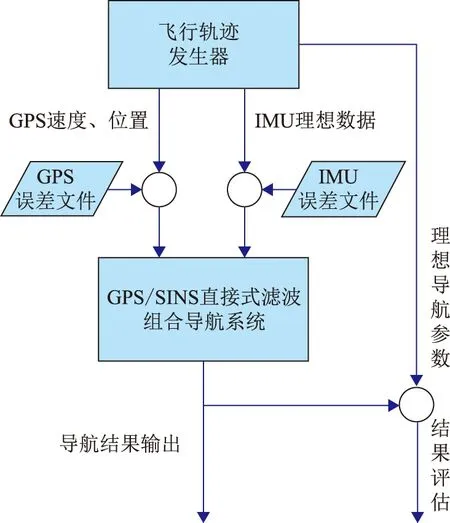
图1 UKF直接式滤波仿真系统结构图Fig.1 Structure chart of the UKF direct filtering demonstration system

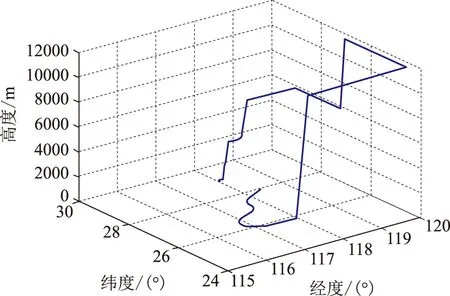
图2 飞行仿真的航迹Fig .2 Simulation of the flight trace

微小型飞行器的初始姿态定为：飞行器载体水平，航向90°，位置(118°，29°，50m)，UKF滤波初始参数：惯性器件噪声参数，状态初值和初始方差阵的值，UKF中的sigma点伸缩因子等。根据目前在用的惯性器件的性能，设定方差值，设陀螺噪声的均方根为0.5(°)/s，设加速度计噪声的均方根为10-3g，设GPS测速误差为0.5m/s，定位误差8m。

基于UKF的GPS/SINS组合导航仿真系统得到的姿态曲线如图3所示，姿态误差如图4所示，定位误差分别如图5所示，系统的稳态误差值如表1所示。

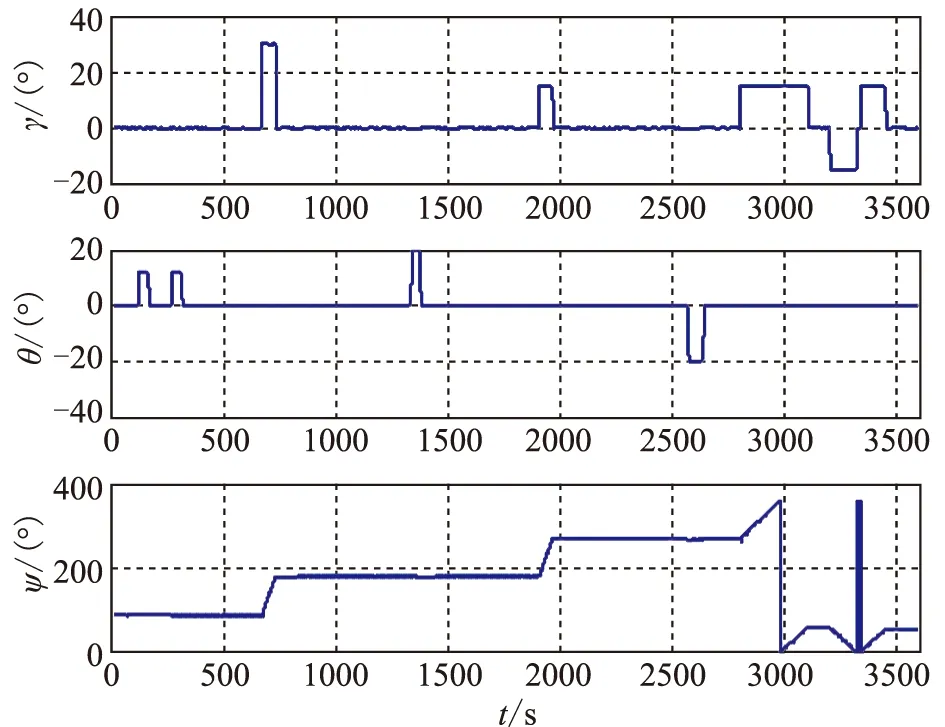
图3 姿态曲线Fig.3 The curve of attitude curve

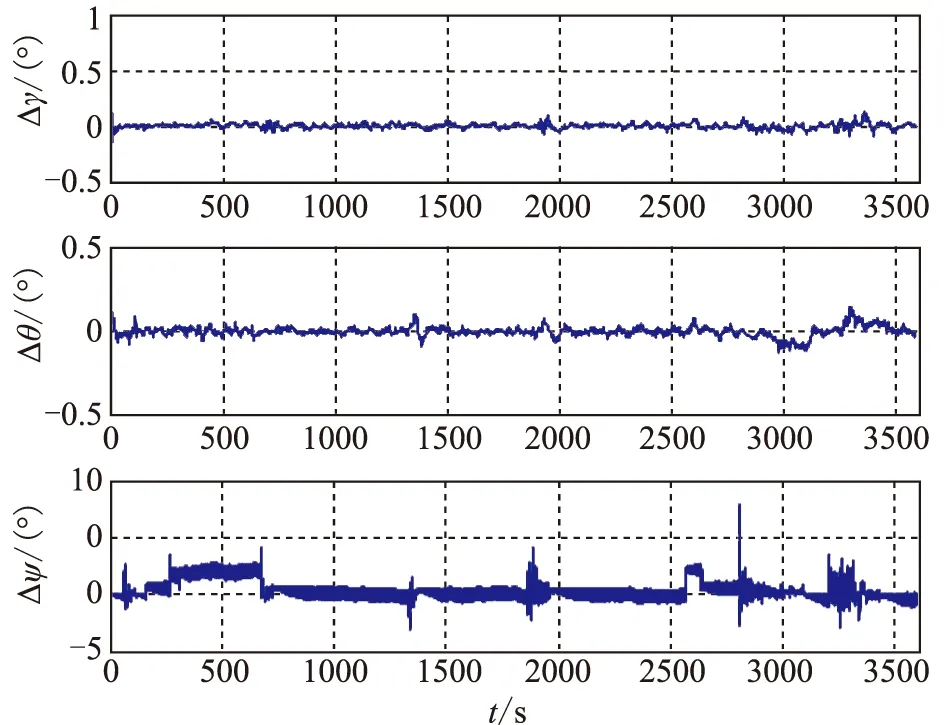
图4 姿态误差曲线Fig.4 The curve of attitude error

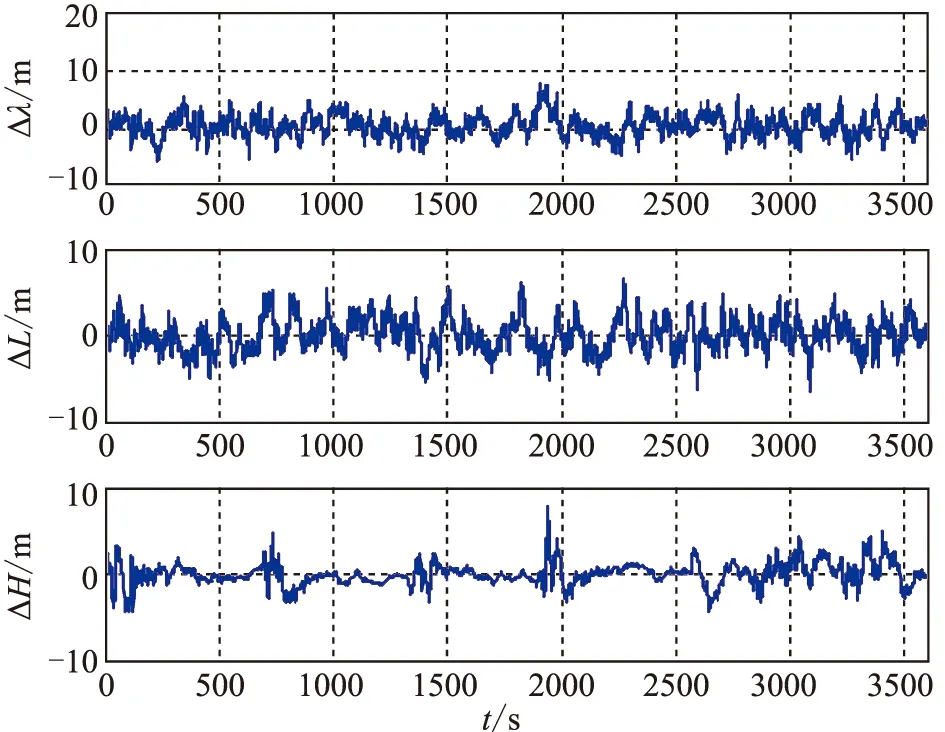
图5 位置误差曲线Fig.5 The curve of position error

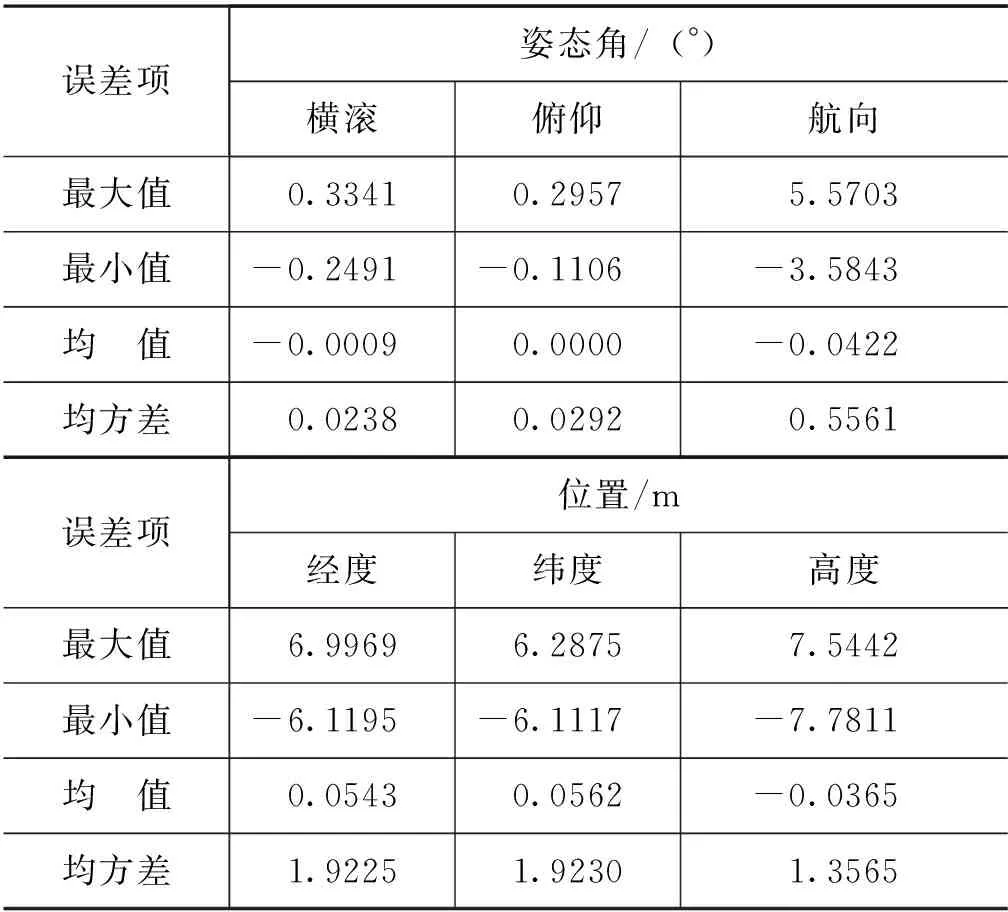
误差项姿态角/(°)横滚俯仰航向最大值0.33410.29575.5703最小值-0.2491-0.1106-3.5843均 值-0.00090.0000-0.0422均方差0.02380.02920.5561误差项位置/m经度纬度高度最大值6.99696.28757.5442最小值-6.1195-6.1117-7.7811均 值0.05430.0562-0.0365均方差1.92251.92301.3565

由仿真图像及数据表明，基于UKF的惯性组合导航直接式滤波方法稳定，姿态误差和位置误差较小，具有较高的导航精度。在微小型飞行器特性的飞行条件下，该直接式滤波方法能够适应于各种飞行状态。

4 结论

本文研究了基于UKF的直接式惯性组合导航滤波方法，建立直接式结构的卡尔曼滤波器，以导航参数作为状态变量，以GPS系统的速度和位置组成观测向量，实现了直接式滤波计算流程。利用方向余弦矩阵和姿态角间的关系，实现了状态向量中姿态角sigma点的生成与各sigma点姿态角误差均值及方差的计算。本文构建了GPS/SINS组合导航直接式卡尔曼滤波仿真验证系统，仿真结果验证了该直接式非线性滤波方法的有效性，采用此方法可有效避免将非线性滤波模型进行线性化后的误差，适于解决高机动条件下飞行器滤波及状态估计。

[1] 刘建业，曾庆华，赵伟,等.导航系统理论与应用[M].西安:西北工业大学出版社,2010：296-366.

[2] 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998:198-221.

[3] 高社生，何鹏举，杨波等.组合导航原理及应用[M].西安:西北工业大学出版社,2012:92-108.

[4] 林雪原，刘华章，史佩.一种低成本、低精度SINS/GPS组合导航系统级试验研究[J].武汉大学学报(信息科学版)，2006(10).

[5] 林雪原，林炳荣.基于量测多尺度预处理的GPS/SINS组合导航系统[J].兵工自动化，2010(7).

[6] 林雪原.GPS/SINS组合导航系统与实现[J].计算机测量与控制，2007(12).

[7] 林雪原，骆卉子，范文强.一种改进的GPS动态定位滤波方法[J].海军航空工程学院学报，2010(4).

[8] 林雪原.GPS/SINS组合导航系统的多尺度融合算法研究[J].电子科技大学学报，2011(9).

[9] 陆海勇.捷联惯性导航系统中UKF滤波技术的应用研究[D].南京：硕士学位论文,南京航空航天大学, 2008.

[10] 周菊华.UKF滤波方法在捷联惯导系统中的应用研究[D].南京：硕士学位论文,东南大学,2009.

[11] 徐佳.INS/GPS组合导航系统滤波算法的研究[D].沈阳：硕士学位论文,东北大学,2006.

[12] 刘铮.UKF算法及其改进算法的研究[D].长沙：硕士学位论文,中南大学,2009.

[13] 徐佳鹤，井龙伟.UKF滤波算法在INS/GPS组合导航系统中的研究[C]//.中国控制与决策学术年会论文集, 2007: 213-216.

[14] S J Julier, J K Uhlmann. Unscented Filtering and nonlinear Estimation[A]. Proceeding of the IEEE[C]//.vol.92 No3, March 2004.

Direct Kalman Filtering Algorithm for the GPS/SINS Integrated Navigation Based on UKF

WANG Lin1，LIN Xue-yuan2

(1.Naval Aeronautical and Astronautical University Graduate Students’ Brigade,Yantai 264000,China;2.Research Institute of Information Fusion, Yantai 264000,China)

A Kalman filter with direct structure is proposed based on UKF filter. The direct filter takes 9 parameters as state vectors such as attitude, velocity and position. And the six-dimension observation vectors are made up of velocity and position provided by Global Positioning System. The filter directly describes navigation parameters dynamic process of the system and reflects the evolution of motion state. A direct filtering demonstration system for the GPS/SINS Integrated Navigation is constructed according to the characteristics of GPS/SINS integrated navigation system. The simulation results verifies the effectiveness of the direct Kalman filtering method based on UKF and the filtering method can improve the navigation accuracy.

Inertial integrated navigation; Unscented Kalman filter; Direct filtering

2015 - 02 - 05；

2015-03-12。

国家自然科学基金(60874112)

王林(1982 - )，男，硕士研究生，主要从事有关信息传输与处理技术方向的研究。

E-mail:wl19820416@sohu.com

TP273

A

2095-8110(2015)03-0043-06