再入飞行器多变量稳定裕度研究
曹玉腾 倪少波
北京航天自动控制研究所,北京100854
再入机动飞行器往往飞行马赫数高、机动范围大,造成俯仰、偏航和滚动三通道耦合强烈,此类控制对象本质上为MIMO系统,采用基于多变量控制的相关理论和方法是解决这类飞行器姿态控制系统设计的有效方法,且多变量系统稳定裕度统计方法较传统的基于单通道稳定裕度计算方法更能反映这类飞行器控制系统的稳定程度。
传统稳定裕度分析方法主要基于SISO系统,不能分析通道间耦合引起的不确定性。随着控制理论的发展,目前MIMO系统稳定裕度分析方法大致有以下几种:回差矩阵奇异值方法、基于结构奇异值的μ分析方法、实多回路稳定分析法、Gershgorin圆盘法和稳定超球面法等。其中回差矩阵奇异值法引入传统基于SISO系统幅值裕度和相位裕度的概念,解决了MIMO系统的稳定裕度,因此在工程上得到了较广泛的应用[1]。该方法优点是计算简单,易于工程实现,缺点是计算保守性较大,为此Doyle提出采用结构奇异值分析不确定系统稳定裕度的μ方法[2],该方法在改善计算保守性方面有一定的优势,并在国内飞行控制领域得到了一定的应用[3]。
本文在回差矩阵奇异值法的基础上进行了改进,提出了摄动矩阵迭代法,由计算结果与回差矩阵奇异值法相比,摄动矩阵迭代法大大改善了计算系统稳定裕度的保守性,且计算结果较为可靠。
1 回差矩阵奇异值法[4]
通过图1讨论采用回差矩阵奇异值计算多变量系统稳定裕度。图1(a)中,G(s)为多变量控制对象,F(s)为反馈控制器,图1(b)中,矩阵 L=diag(l1,l2,…,ln)为附加的摄动矩阵,其中 li(i=1,2,…,n)是可变的复数,用来检测系统在发生摄动情况下的鲁棒性。

图1 多变量控制系统结构
在图1所示的系统中,所加入的摄动矩阵L形式为

其中,Ki,φi分别为摄动矩阵某一通道的增益和相位。如果系统正常工作,无摄动发生,则Ki=1,φi=0,即L矩阵为单位阵。
如图1(b)所示系统,若加入摄动系统L(s)后闭环系统保持稳定,这意味着系统的回差阵是非奇异的,有以下关系成立

以及摄动增益不变,允许摄动相位的变化范围,即多变量系统的相位裕度

由此可得,所有回路的增益或相位可以在由式(4)和(5)计算得到的幅值或相位裕度范围内变化,不会导致系统不稳定。但由于式(3)是闭环系统稳定的充分条件,故通过该方法计算多变量系统稳定裕度存在保守性。
2 摄动矩阵迭代法
针对回差矩阵奇异值法计算保守性较大的问题,本文研究了摄动矩阵迭代法,该方法以回差矩阵奇异值法为基础,通过回差矩阵奇异值法计算系统稳定裕度,并构造系统的摄动矩阵,通过不断增加摄动矩阵的增益和相位,使摄动后的系统逐渐逼近临界稳定状态,从而得到多变量系统真正的稳定裕度。
2.1 设计思路
摄动矩阵迭代法的设计思路如图2所示,首先应用回差矩阵奇异值法计算多变量控制系统的稳定裕度,根据稳定裕度计算结果构成摄动矩阵L1,将L1串入多变量系统,再次应用回差矩阵奇异值法计算稳定裕度,并得到 L2,再将L2串入系统,计算L3,如此不断循环。每一步的迭代需首先判断当前系统的闭环特征根,若闭环特征根全部为负,则继续迭代,否则跳出迭代。最终得到系统幅值裕度和相位裕度为L=L1L2…Ln的增益和相位。
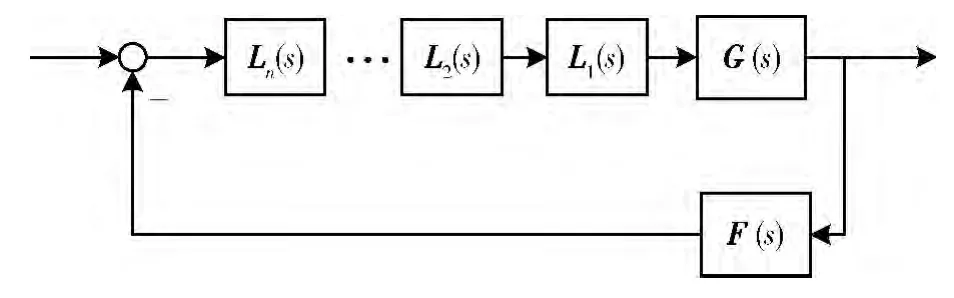
图2 摄动矩阵迭代法原理框图
2.2 设计步骤
以飞行器某一特定飞行状态对应的相位裕度为例来具体说明摄动矩阵迭代法的计算步骤:
1)应用回差矩阵奇异值法初步计算多变量系统相位裕度,有以下关系成立

计算可得ω∈(0,+∞)范围内,系统回差矩阵最小奇异值为0.531,对应频率值为113rad/s,最小奇异值随频率的变化关系见图3。
多变量系统的幅值裕度和相位裕度分别为




3)将摄动矩阵L1串入系统,计算此时闭环系统特征根位于复平面右边平面的个数p0,若p0=0,则返回步骤2);若p0≠0,则停止计算,若迭代超过10次,则停止运算。

图3 最小奇异值随频率变化关系曲线
经摄动矩阵迭代法计算得到系统最终的相位裕度为50.22,同理也可应用摄动矩阵迭代法计算系统幅值裕度,该方法的算法流程如图4所示。
将摄动矩阵迭代法和回差矩阵奇异值法计算的多变量系统稳定裕度进行对比,如表1所示。
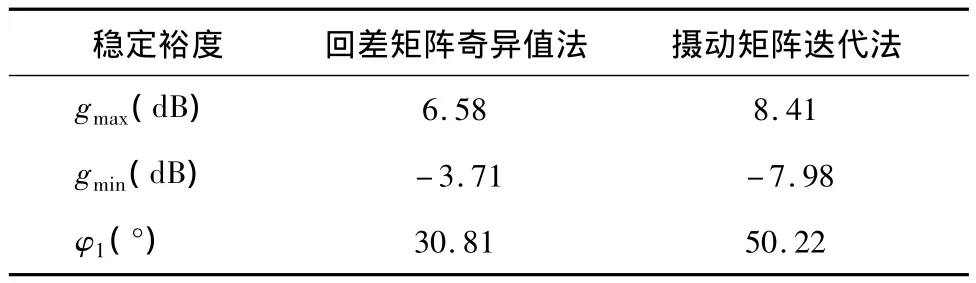
表1 多变量控制系统的稳定裕度

图4 摄动矩阵迭代法流程图
应用改进的稳定裕度计算方法,系统的幅值裕度和相位裕度均有了明显改善,大大减小了稳定裕度计算的保守性。和单通道稳定裕度相比,摄动矩阵迭代法计算的系统稳定裕度从多变量的角度更真实的反映了多变量控制系统的稳定裕度。
3 仿真验证
根据多变量系统的幅值裕度和相位裕度确定摄动矩阵L,代入控制系统定点仿真模型中进行仿真。其中摄动矩阵L分别为:

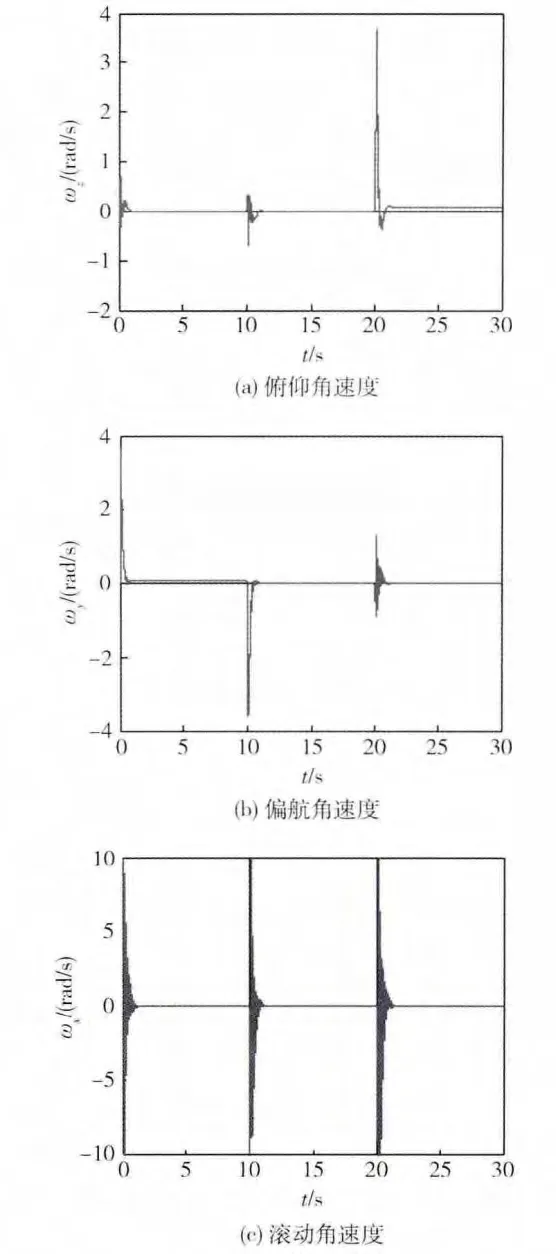
图5 仿真状态1
由以上仿真结果中可以得出:仿真状态1中,系统出现高频振荡,但最终趋于稳定,说明此时系统接近发散;仿真状态2中,相较于仿真状态1,系统的高频振荡较小,说明gmax还有进一步提高的空间;仿真状态3中,系统出现低频振荡并且临近发散,此时gmin的保守性也很小。综合比较起来,PM,gmax,gmin三项稳定指标的保守性均很小,其中PM与gmin最接近系统真实的裕度。
4 结论
应用多变量控制理论,通过计算多变量系统回差矩阵的最小奇异值,得到多变量系统的幅值裕度和相位裕度。针对该方法在计算稳定裕度时的保守性,采用摄动矩阵迭代法大大改善了其保守性,且效果较佳。并通过仿真证明了摄动矩阵迭代法计算系统稳定裕度保守性小,且可靠性较高。
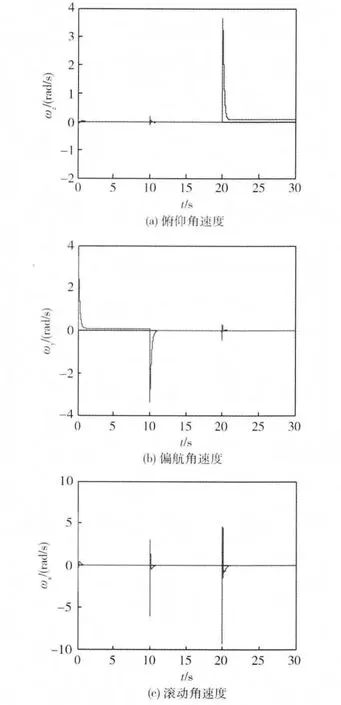
图6 仿真状态2

图7 仿真状态3
[1] 李帆.不确定性系统的解耦控制与稳定裕度分析[D].西安:西北工业大学2001.(LI Fan.The Decoupling Control Study and Stability Margin Evaluation of Multivariable Uncertain Systems[D].Xi'an:A Dissertation Submitted for the Degree of Ph.D of Northwestern Polytechnical University,2001.)
[2] Doyle J C.Analysis of feedback systems with structured uncertainties[J].IEEE Proceedings,Part D,1982,129(6):242-250.
[3] 李洪超,史忠科.多变量飞控系统稳定裕度的μ分析方法研究[J].飞行力学,2006,24(2):31-34.(Li Hongchao,Shi Zhongke.Study of μ analysis method for evaluation of stability margin of a multivariable flight control system[J].Flight Dynamics,2006,24(2):31-34.)
[4] 吴斌,程鹏.多变量飞控系统的稳定裕度分析[J].航空学报,1998,19(6):657-661.(Wu Bin,Cheng Peng.Stability margin analysis of the multiloop flight control systems[J].Acta Aeronautica et Astronautica Sinica,1998,19(6):657-661.)
[5] 周克敏.鲁棒与最优控制[M].北京:国防工业出版社,2001.(Zhou Kemin.Robust and Optimal Control[M].Beijing:National Defend Industry Press,2001.)

